Моделирование и анализ данных
2019. Том 9. № 2. С. 83–98
ISSN: 2219-3758 / 2311-9454 (online)
Алгоритм внешней аппроксимации выпуклого множества допустимых управлений для дискретной системы с ограниченным управлением
Аннотация
Общая информация
Ключевые слова: Дискретная система управления, задача быстродействия, оптимальное позиционное управление, задача линейного программирования, множество управляемости, выпуклый многогранник, ограниченный полиэдр, выпуклый компакт, полиэдральная аппроксимация
Рубрика издания: Теория управления
Тип материала: научная статья
Для цитаты: Ибрагимов Д.Н., Порцева Е.Ю. Алгоритм внешней аппроксимации выпуклого множества допустимых управлений для дискретной системы с ограниченным управлением // Моделирование и анализ данных. 2019. Том 9. № 2. С. 83–98.
Полный текст
В работе рассматривается задача быстродействия для линейной дискретной системы с ограниченным множеством управления. Исследуется достаточное условие применимости аппроксимации выпуклого множества управления для оценки точности гарантирующего решения.
1. ВВЕДЕНИЕ
Задача быстродействия является классической задачей теории оптимального управления, обладающей естественным функционалом качества.
Изначально данная задача была сформулирована для систем с непрерывным временем и полностью решена для случая линейных ограничений на управление.
Решение, основанное на принципе максимума [1-3] и методе динамического программирования [4], гарантирует, что управление будет релейно, то есть будет являться кусочнопостоянной функцией с конечным числом точек переключения и значениями в вершинах множества допустимых управлений.
Задачи оптимального управления для систем с дискретным временем в общем случае имеют ряд существенных отличий от аналогов с непрерывным временем. Зачастую они сводятся к решению задач выпуклого и линейного программирования [2,6,7,8]. Иногда удается получить результат, известный как дискретный принцип максимума [6]. Тем не менее, в случае дискретного времени традиционные методы теории оптимального управления оказываются неэффективны при решении задачи быстродействия. Более того, доказано, что формальное применение дискретного принципа максимума дает некорректные результаты [9,10].
Данные проблемы обусловленным дискретным характером критерия качества управления — времени, необходимого для достижения системой начала координат, что приводит к неединственности оптимального управления почти для всех начальных состояний. Актуальным оказывается поиск более эффективных методов.
В работах [9,11,12] рассмотрен метод решения поставленной задачи на основе класса множеств 0-управляемости — множеств тех начальных состояний, из которых система может быть переведена в начало координат за фиксированное число шагов. Алгоритм решения базируется на идее перевода состояния системы на каждом шаге в множество 0- управляемости за меньшее число шагов. В качестве критерия принадлежности состояния множеству используется функционал Минковского. В [11] продемонстрировано, что в случае линейных ограничений на управление задача быстродействия может быть полностью сведена к решению ряда ЗЛП. Однако аналогичный подход для случая выпуклых множеств допустимых управлений приводит к сложным задачам нелинейного математического программирования.
Данный факт делает актуальным решение задачи об аппроксимации множества допустимых управлений вложенным в него многогранником: решение задачи быстродействия для меньшего множества допустимых управлений будет являться гарантирующим решением в исходной задаче. Подобные задачи рассматривались в различных постановках прежде: например, в [13] предложен алгоритм аппроксимации а- ядра для решения задачи квантильной оптимизации с билинейной функцией потерь.
Для увеличения точности гарантирующего решения требуется определить критерий качества аппроксимации и построить алгоритм, позволяющий добиться сколь угодно малой величины этого критерия.
Решение поставленной задачи базируется на свойствах выпуклых множеств, рассмотренных в качестве точек метрических пространств [14-19].
Как известно [19], класс выпуклых многогранников является всюду плотным в пространстве компактов с метрикой Хаусдорфа. Данный факт гарантирует, что задача об аппроксимации может быть разрешена. В [12] разработан алгоритм, позволяющий приблизить произвольное выпуклое компактное множество (вписанным) в него многогранником, и доказана сходимость в смысле метрики Хаусдорфа.
Тем не менее, алгоритм, изложенный в [12], не позволяет оценить качество гарантирующего решения, что приводит к актуальности решения задачи об аппроксимации множества допустимых управлений (описанным) вокруг него многогранником. В этом случае оптимальное значение критерия для вспомогательной системы будет не больше, чем для исходной. В то время, как согласно [12] минимальное число шагов, необходимое для достижения 0, у вспомогательной системы будет не меньше, чем у исходной. В работе приведен обзор методов решения задачи быстродействия, изложенных в [9,11,12]. Также построен алгоритм внешней аппроксимации, который базируется на идее, разработанной в [13], которая заключается в процедуре построения равномерной сетки на n-мерном кубе, использующейся как множество нормалей к опорным гиперплоскостям выпуклого компакта.
Доказана сходимость разработанного алгоритма в смысле метрики Хаусдорфа. Эффективность новых методов опробована на примере решения задачи демпфирования высотного сооружения [20].
2. ПОСТАНОВКА ЗАДАЧИ
Решается задача быстродействия для линейной дискретной системы с ограниченным управлением в виде выпуклого компактного множества:


3. ДОПОЛНИТЕЛЬНЫЕ ПОСТРОЕНИЯ




Для оценки снизу минимального числа шагов необходима аппроксимация сверху множества допустимых управлений.
4. АЛГОРИТМ ВНЕШНЕЙ АППРОКСИМАЦИИ


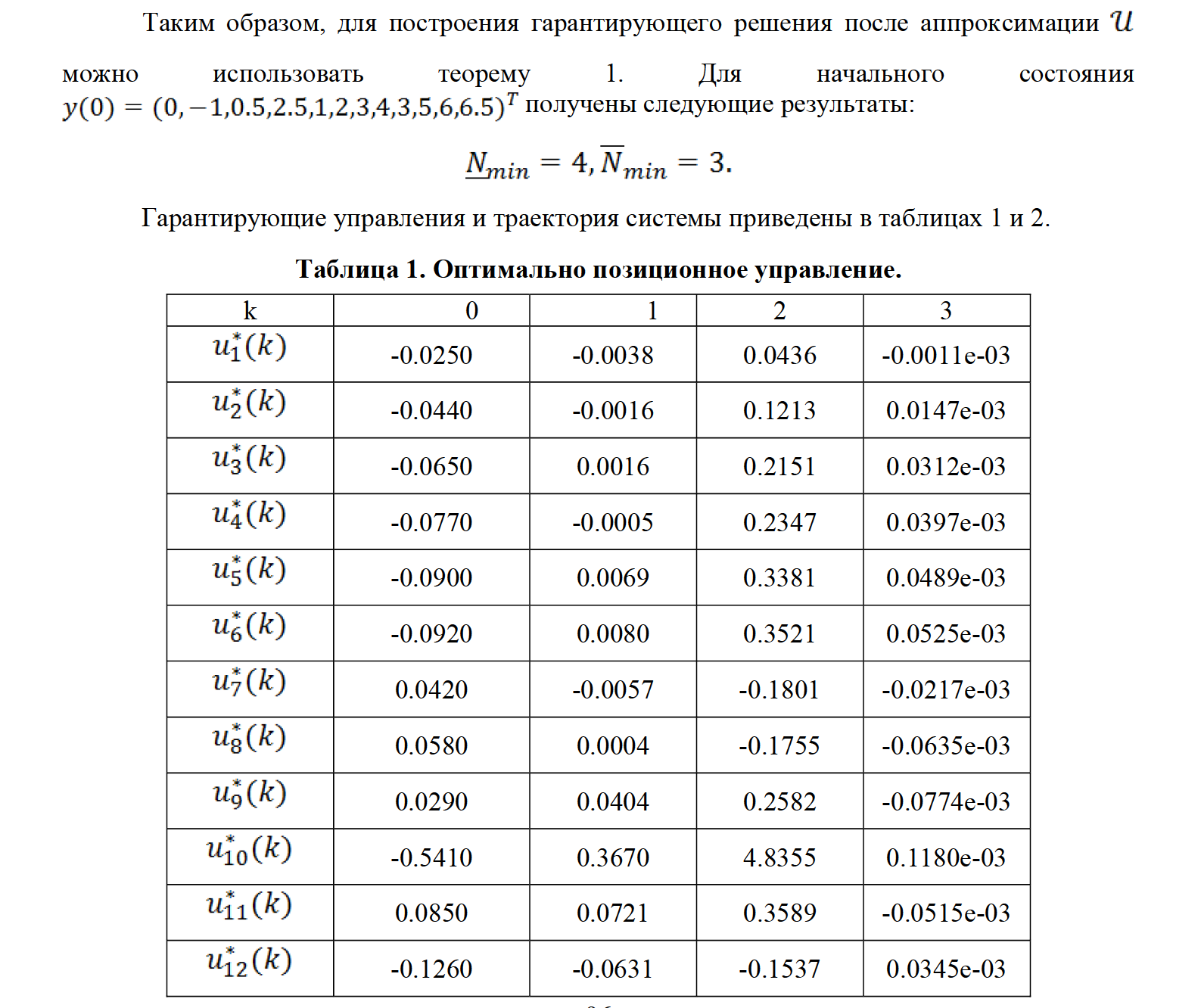
Таким образом, получив оценку снизу минимального числа шагов, за которое возможно перевести систему из начального положения в ноль, можно рассуждать о качестве нижней аппроксимации множества допустимых управлений. Улучшая аппроксимацию, можно получить более точное решение. Запишем алгоритм внешней аппроксимации выпуклого множества допустимых управлений.
Алгоритм 2. Алгоритм внешней аппроксимации выпуклого множества допустимых управлений

5. ЗАДАЧА ДЕМПФИРОВАНИЯ ВЫСОТНОГО СООРУЖЕНИЯ
Эффективность предложенных методов продемонстрирована на примере решения задачи демпфирования здания, расположенного в зоне сейсмических активностей. Данная модель была рассмотренна в [20].
Из-за сейсмических активностей возникают колебания сооружений, которые способствуют потере устойчивости и разрушению строения. Для гашения таких колебаний разработана задача управления сооружением по принципу обратной связи, за счёт дополнительных прикладываемых сил на это сооружение. Известны и широко применимы два совершенно противоположных метода управления сооружения по принципу обратной связи, а именно: динамическое гашение колебаний с использованием дополнительных материальных тел и виброзащита, предполагающая изоляцию сооружения от подвижного основания. Один из возможных вариантов технической реализации динамического гашения колебаний заключается в создании специального этажа с размещением на нем некоторой достаточно малой массы (по сравнению с общей массой сооружения), перемещаемой в соответствии с законом управления в форме обратной связи по текущим показаниям датчиков, что позволяет оказывать управляющее воздействие на данный этаж.
В качестве механической системы, моделирующей колебания высотного сооружения, будем рассматривать одномерную цепочку упругосвязанных материальных точек (этажей или секций сооружения), одна из которых (основание) совершает поступательное движение, порождаемое сейсмическим воздействием. Предполагается, что масса основания намного превышает массы остальных материальных точек и поэтому влиянием движения секций сооружения на движение основания можно пренебречь. В дальнейшем будем считать, что массы всех материальных точек одинаковы, а упругие и демпфирующие связи моделируются линейными элементами с одинаковыми коэффициентами упругости и демпфирования.
Уравнения движения рассматриваемой системы имеют вид:


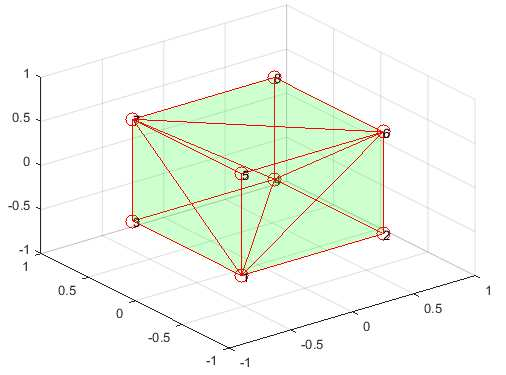
Рис. 1. Аппроксимация U снизу для 8 точек
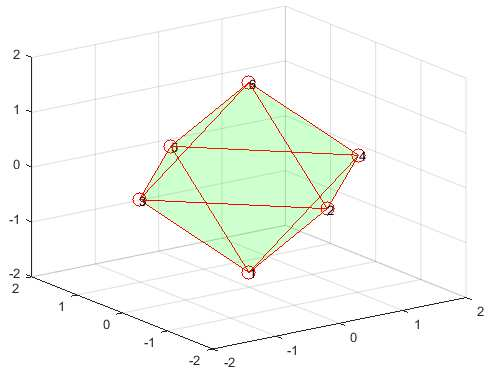
Рис. 2. Аппроксимация U сверху для 8 точек
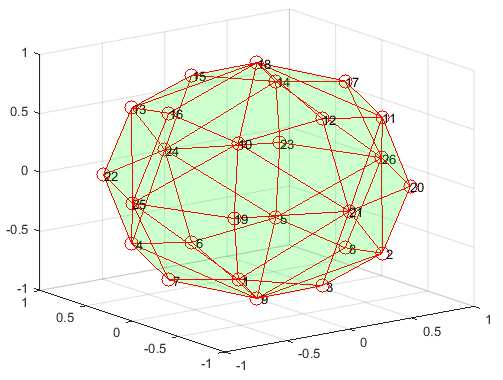
Рис. 3. Аппроксимация U снизу для 27 точек
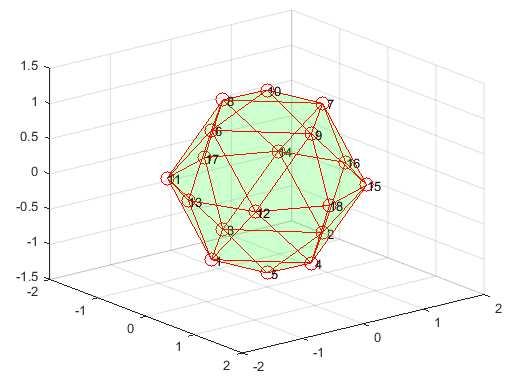
Рис. 4. Аппроксимация U сверху для 27 точек
5. ЗАКЛЮЧЕНИЕ
В работе рассмотрена задача быстродействия для линейных дискретных систем с ограниченным управлением. Рассматривалось множество управлений в виде выпуклого компакта. Для решения данной задачи разработан алгоритм внешеней аппроксимации множества допустимых управлений. Доказана теорема о сходимости аппроксимированного множества к исходному множеству. Построен метод оценки критерия качества гарантирующего решения в задаче быстродействия для линейной дискретной системы с ограниченным управлением.
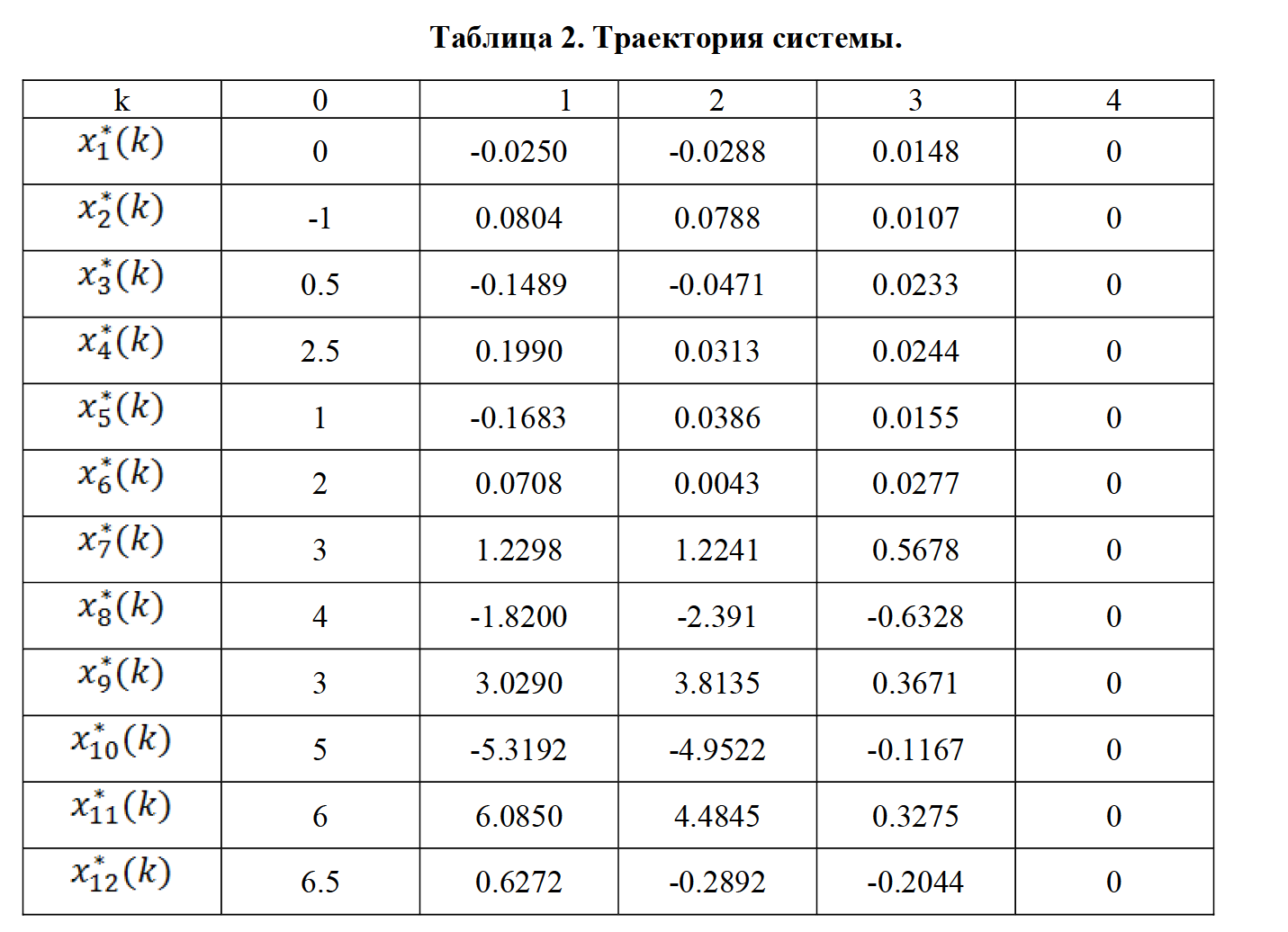
Отдельно рассмотрена задача быстродействия для демпфирующей системы здания в зоне сейсмических активностей. Произведена дискретизация непрерывной системы. Для заданного множества допустимых управлений в виде трёхмерного шара проведена аппроксимация по предложенному алгоритму и приведены иллюстрации. Найдено гарантирующее управление и траектория системы.
ФИНАНСИРОВАНИЕ
Работа выполнена при финансовой поддержке гранта РФФИ № 18-08-00128-а.
Литература
- Понтрягин Л.С., Болтянский В.Г., Гамкрелидзе Р.В., Мищенко Б.Ф. Математическая теория оптимальных процессов. М.:Наука, 1969.
- Болтянский В.Г. Математические методы оптимального управления. М.:Наука, 1969.
- Аграчев А.А., Сачков Ю.Л. Геометрическая теория управления. М.:Наука, 2005.
- Беллман Р. Динамическое программирование. М.:ИИЛ, 1960.
- Болтянский В.Г. Оптимальное управление дискретными системами. М.:Наука, 1973.
- Пропой А.И. Элементы теории оптимальных дискретных процессов. М.:Наука, 1973.
- Квакернаак Х., Сиван Р. Линейные оптимальные системы управления. М.:Мир, 1977.
- Табак Д., Куо Б. Оптимальное управление и математическое программирование. М.:Наука, 1975.
- Ибрагимов Д.Н., Сиротин А.Н. О задаче оптимального быстродействия для линейной дискретной системы с ограниченным скалярным управлением на основе множеств 0- управляемости // Автоматика и Телемеханика. 2015. №9. С.3-30.
- Fisher M.E., Gayek J.E. Estimating Reachable Sets for Two-Dimensional Linear Discrete Systems // J. Optim. Theory Appl. 1988. V.56. No.1. P.67-88.
- Ибрагимов Д.Н. Оптимальное по быстродействию управление движением аэростата // Труды МАИ. 2015. №83.
- Ибрагимов Д.Н. Аппроксимация множества допустимых управлений в задаче быстродействия линейной дискретной системой // Труды МАИ. 2016. №87.
- Васильева С.Н., Кан Ю.С. Метод решения задачи квантильной оптимизации с билинейной функцией потерь // Автоматика и телемеханика. 2015. №9. С.83-101.
- Половинкин Е.С., Балашов М.В. Элементы выпуклого и сильно выпуклого анализа. М.:ФИЗМАТЛИТ, 2004.
- Колмогоров А.Н., Фомин С.В. Элементы теории функций и функционального анализа. М.:ФИЗМАТЛИТ, 2012.
- Кроновер Р.М. Фракталы и хаос в динамических системах. М.:Постмаркет, 2000.
- Схрейвер А. Теория линейного и целочисленного программирования. Т. 1, 2. М.: Мир, 1991.
- Овсеевич А.И., Черноусько Ф.Л. Свойства оптимальных эллипсоидов, приближающих области достижимости системы с неопределённостями // Известия РАН. Теория и системы управления. 2004, №4. С.8-18.
- Берже М. Геометрия. Том 2. М.:МИР, 1984.
- Баландин Д.В., Коган М.М. Синтез законов управления на основе линейных матричных неравенств. М.:Физматлит, 2007.
- Дж. фон Нейман. Теория игр и экономическое поведение. М.: Наука, 1970. - 708 с.
Информация об авторах
Метрики
Просмотров
Всего: 493
В прошлом месяце: 2
В текущем месяце: 2
Скачиваний
Всего: 244
В прошлом месяце: 3
В текущем месяце: 0