Вестник практической психологии образования
2012. Том 9. № 3. С. 30–33
ISSN: 2658-3100 (online)
О логике формирования познавательных универсальных учебных действий (на материале знаково-символических действий)
Аннотация
Общая информация
Рубрика издания: Научная обоснованность реализуемых в системе образования практик психолого-педагогической работы с детством
Тип материала: научная статья
Для цитаты: Гуружапов В.А. О логике формирования познавательных универсальных учебных действий (на материале знаково-символических действий) [Электронный ресурс] // Вестник практической психологии образования. 2012. Том 9. № 3. С. 30–33. URL: https://psyjournals.ru/journals/bppe/archive/2012_n3/Guruzhapov (дата обращения: 19.04.2024)
Полный текст
Согласно ФГОС начального общего образования, формирование универсальных учебных действий является важнейшей составляющей основной образовательной программы школы [15]. Среди познавательных универсальных учебных действий необходимо обратить особое внимание на знаково-символические действия, а именно: моделирование — преобразование объекта из чувственной формы в модель, где выделены существенные характеристики объекта, и преобразование модели для выявления общих законов, определяющих данную предметную область, в чистом виде. Это действительно важнейшие действия (будем называть их действиями моделирования), обеспечивающие успешность учения, так как свойства и закономерности изучаемого школьниками окружающего мира представлены им в основном в виде моделей.
Логика формирования действий моделирования была достаточно подробно описана В.В. Давыдовым применительно к задачам проектирования учебной деятельности в развивающем обучении [4, 5, 6]. Согласно этой логике, способность к осуществлению действий моделирования развивается в процессе решения так называемых учебных задач. Общепринятое рабочее определение учебной задачи следующее: учебной называется такая задача, которая вынуждает ученика искать общий способ решения всех задач данного типа. В этой форме она де-факто присутствует уже в книге В.В. Давыдова «Виды обобщения в обучении» [4]. Позднее он дает ей развернутое определение: «Учебная задача, которая школьникам предлагается учителем, требует от них: 1) анализа фактического материала с целью обнаружения в нем некоторого общего отношения, имеющего закономерную связь с различными проявлениями этого материала, т. е. построения содержательной абстракции и содержательного обобщения; 2) выведения на основе абстракции и обобщения частных отношений данного материала и их объединения (синтеза) в некоторый целостный объект, т. е. построения его “клеточки” и мысленного конкретного объекта; 3) овладения в этом аналитико-синтетическом процессе общим способом построения изучаемого объекта» [6].
При решении учебной задачи школьники раскрывают происхождение «клеточки» изучаемого целостного объекта и, используя ее, мысленно воспроизводят этот объект. Тем самым при решении учебной задачи школьники осуществляют некоторый микроцикл восхождения от абстрактного к конкретному как путь усвоения теоретических знаний [5, с. 151152].Важно отметить, что учебная задача есть объективный результат логико-психологического анализа содержания учения. Ее можно рассматривать относительно независимо от многообразия условий обучения детей. В теории развивающего действия моделирование возникает не само по себе, а в ходе протекания особого процесса, в ходе которого ученик открыл для себя «некоторое общее отношение, имеющее закономерную связь с различными проявлениями этого материала», то есть когда он увидел в конкретной задаче нечто имеющее что-то принципиально общее с другими задачами этого типа. Поэтому первое учебное действие, посредством которого решается учебная задача, есть «преобразование условий задачи с целью обнаружения всеобщего отношения изучаемого объекта». Это действие можно выполнить только в том случае, если проанализированы условия задачи и выделены существенные признаки и отношения анализируемых объектов, представленных в условии задачи. И только потом за ним следуют такие действия, как «моделирование выделенного отношения в предметной, графической или буквенной форме; преобразование модели отношения для изучения его свойств в “чистом виде”» [5, с. 154].
Итак, логика формирования знаково-символических действий как познавательных универсальных учебных действий связана с общей логикой решения учебных задач, то есть задач квазиисследовательско- го типа. В ходе решения таких задач ученик приобретает опыт осмысления выделения существенных отношений в условиях задач и построения на их основе модели изучаемого объекта. Он осознает, что переход от объекта к его модели не совершается сам по себе, что нужно подумать, какие свойства объекта нужно моделировать и для чего.
Момент перехода от объекта к его модели как особой мыслительной работе постоянно ускользает от внимания педагогов, вынужденных заниматься проектированием учебного процесса в русле требований ФГОС. Этот момент не прорабатывается на уроке с учениками. Учителя предлагают ученикам модель в готовом виде, не обсуждая условия и цели ее появления. В качестве примера рассмотрим сценарий фрагмента урока по математике для 2 класса по учебнику Л.Г. Петерсон, разработанный учителем начальных классов Л.А. Деветьяровой. Он представлен в интернете в рамках Общероссийского проекта «Школа цифрового века» 2012-2013 на «Фестивале педа
гогических идей “Открытый урок”» [9].
«Прием моделирования используется и при рассмотрении умножения суммы на число (распредели
тельное свойство умножения) на 28-м уроке по учебнику «Математика-2» для 2 класса. В устные упражнения вместе с примерами на повторение включается пример 24-7, который вызывает затруднения у учеников, создается проблемная ситуация, мотивирующая поиск нового вычислительного приема.
— Используем имеющиеся у нас знания.
— Разбейте число 24 на два таких слагаемых, каждое из которых мы уже умеем умножать на 7. Какое выражение получилось? (20+4)-7.
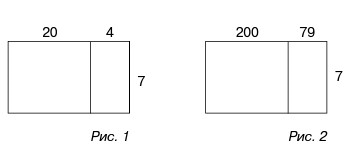
— Воспользуемся графической моделью умножения (рис. 1).
— Найдите площадь прямоугольника, одна сторона которого 20+4, а другая — 7.
— Удобнее найти площадь каждого прямоугольника отдельно, полученные результаты сложить.
24-7 = (20+4)-7=20-7+4-7 = 168
Вывод. Умножение двузначного числа на однозначное сводится к умножению суммы на число (распределительное свойство умножение)».
Рассмотрим подробнее момент перехода от объекта (20+4)-7 к его модели (рис. 1).
Числу 24 ставится в соответствие сторона прямоугольника длиной (20+4), числу 7 — другая сторона прямоугольника длиной 7. Площадь данного прямоугольника отождествляется с результатом следующего арифметического действия: (20+4)-7. В качестве аргумента приводится удобство вычисления. То есть ученики должны рассмотреть не существенные свойства объекта и способы их отображения в модели, а что-то третье, в данном случае удобство вычисления. В данном случае такой подход снижает значение модели.
Проведем мысленный эксперимент. Пусть надо вычислить 279-7. С такими задачами ученик могут встретиться уже в 3-4 классе в зависимости от используемой программы. Будем действовать так, как предлагается в сценарии: представим арифметическое выражение (200+79)-7 в виде площади прямоугольника (рис. 2).
Очевидно, что использование такой модели отнюдь не облегчает ученикам вычисление.
Конечно, использованный учителем прием не повредит ученикам, но и не продвинет их в освоении и понимании способов моделирования. Модель была бы нужна для анализа или подтверждения распределительного закона умножения (а+в)-с = (а-с)+(в-с). Но эта задача не была поставлена, хотя в выводе она присутствует.
С точки зрения деятельностного подхода, учебная задача должна обращать внимание ученика на предмет и способы действия с этим предметом. В большинстве случаев учителя понимают это, но не учитывают психологическую логику самой ситуации постановки задачи. В результате появляются в сценариях урока сомнительные вопросы. В качестве примера рассмотрим сценарий фрагмента урока математики, который представила учитель начальных классов Т.И. Алехина на «Фестивале педагогических идей “Открытый урок”» [1]:
«5. Математическое моделирование.
Задача. У мальчика 50 коп. Яблоко стоит а коп., а груша к коп. О чем мальчик думает при выполнении каждого из следующих действий?
50-а 50:к а+к 50-а3 50-а-к (а+к)2 а-к 50-к а-4 50-(а+к) (50-а)к а-9-50
Поставьте вопрос задачи и выберите нужную модель.
Мой многолетний опыт подтверждает целенаправленность такого приема решения задач. Детей увлекает такая творческая работа. Они с интересом включаются в поисковую деятельность».
Сомнений в том, что такая задача вызывает интерес у учеников, нет. Сомнение вызывает вопрос «О чем мальчик думает при выполнении каждого из следующих действий?» Мало ли о чем может подумать мальчик при обдумывании 12 алгебраических выражений. Видимо, учитель предполагал, что ученики будут обсуждать различные модели этих выражений и их соотношение с предметной ситуацией. Возможно, в данном классе ученики данного учителя без лишних слов понимают, чем им надо заниматься. Но для проектирования сценария урока для других учителей надо точно ставить вопрос. Если такой вопрос будет поставлен, то придется обсуждать все 12 моделей, а значит продумывать сценарий дискуссии, которая по времени займет весь урок.
Соотношение предметной ситуации и модели, в частности, математической, — труднейший для учителя момент в организации учебной деятельности на уроке. Современные_учебно-методические комплекты насыщены заданиями, связанными с интерпретацией различных сюжетных ситуаций в арифметических действиях. Проблемность этих задач обычно заключается в том, что есть неоднозначность в установлении соотношения объекта и его модели. А потому при решении соответствующих задач учащихся могут анализировать условия адекватности отображения значения сюжета в его математической модели и осуществлять рефлексию способа своих действий с моделью. При проектировании сценария урока необходимо так ставить вопросы и так планировать решение задач, чтобы предметом размышления учащихся была именно множественность решений подобных задач и определения возможных вариантов решения учениками этих задач на уроке. Учителю при проектировании сценария решения задачи надо не сужать, а по возможности расширять зону возможных поисков. Но при этом он вынужден удерживать в качестве цели достижение определенного приемлемого общего для всех учеников результата. Этот результат может обсуждаться как дополнительные условия к формулировке задачи.
В качестве примера рассмотрим следующую задачу из учебника математики для 1-го класса авторского коллектива М.И. Моро [11, с. 52]. Ученикам нужно определить, какой из арифметических примеров можно считать математической моделью для интерпретации смысла сюжетной картинки (рис. 3).
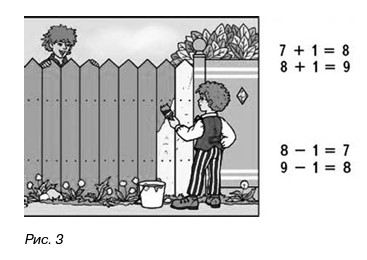
Множественность решений связана с неопределенностью значения наполовину закрашенной доски забора. Поэтому учитель может задать следующий вопрос: «О чем мы должны договориться относительно смысла этой картинки, прежде чем определять, какой пример может быть моделью для описания действий мальчика?» Дети из контекста уроков математики догадываются, что речь идет о количестве закрашенных и незакрашенных досок. Но одна доска закрашена наполовину. Встает вопрос: «Как ее считать, закрашенной или незакрашенной?» В зависимости от этого решения этого вопроса выбор соответствующего арифметического примера будет разным. Предположим, в дискуссии определится, что если наполовину закрашенную доску считать все-таки закрашенной, то подходят примеры: 9-1=8 и 8+1=9. А далее уже можно, опять же в дискуссии, определять смысл картинки по каждой модели. Если выберем модель 9-1=8 , то можно дать следующую интерпретацию: «мальчику надо было покрасить 9 досок, одну он пока еще не покрасил. Сколько он уже покрасил досок?». Если выберем модель 8+1=9, то интерпретация картинки будет другая: «мальчик покрасил 8 досок. Если он покрасит еще одну, то сколько всего будет покрашенных досок?». Дискуссию можно продолжить новым вопросом: «А что будет, если наполовину закрашенную доску считать все-таки незакрашенной?»
Выводы
Проектировать развивающие учебные ситуации, нацеленные на формирование таких познавательных универсальных учебных действий, как знаково-символические действия, возможно. Эта возможность обеспечивается тем, что идеи развивающего обучения, в частности, учебная работа с моделями, проникли в содержание обучения математике практически во все современные учебно-методические комплекты начальной школы. Но чтобы реализовать эту возможность, необходимо выдерживать общую логику в проектировании учебных задач и развивающих учебных ситуаций. Пока практически реализовать эту логику в своей деятельности могут в основном учителя, знакомые с теорией и практикой развивающего обучения.
Поэтому остро стоит вопрос о психолого-педагогической подготовке учителей [8, 9, 12]. В Федеральном государственном стандарте высшего профессионального образования психолого-педагогического направления заложена такая возможность как для будущих учителей и методистов начального образования, так и для педагогов-психологов [14]. Им предстоит в будущем совместно создавать образ современного общего начального образования.
Вместе с тем, необходимо вести фундаментальные и прикладные исследования в области логики и психологии формирования действий моделирования в учебном процессе. Определенный задел в этой области отечественной психологической науки уже есть [2, 3, 11, 16, 17 и др.]. Необходимо развить соответствующие предпосылки в направлении обеспечения практики проектной деятельности учителей по оцени- рованию развивающих учебных ситуаций на уроках согласно ФГОС. И на этой основе создавать новую профессиональную педагогическую культуру.
Литература
-
Алехина Т.И. Развивающие функции моделирования текстовых задач как метод активизации мыслительной деятельности обучающихся на уроках математики в начальных классах. — [Электронный ресурс.] — http://festival.1september.ru/articles/551413/
-
Берцфаи Л.В., Поливанова К.И. Функция действия моделирования в учебной деятельности младшего школьника // Развитие психики школьников в процессе учебной деятельности: Сб. научн. тр. — М., 1983. — С. 70–78.
-
Горбов С.Ф., Чудинова Е.В. Действие моделирования в учебной деятельности школьников (к постановке проблемы) // Психологическая наука и образование. — 2000. — №2.
-
Давыдов В.В. Теория развивающего обучения. — М., 1996.
-
Давыдов В.В. Проблемы развивающего обучения. — М., 1986.
-
Давыдов В.В.. Виды обобщения в обучении. — М., 1972.
-
Деветьярова Л.А. Использование приема моделирования на уроках математики в начальной школе. — [Электронный ресурс.] — http://festival.1september.ru›articles/ 570944/
-
Марголис А.А., Рубцов В.В. Психолого-педагогическая подготовка учителя для новой школы // Образовательная политика. — 2010. — № 5–6 (43–44).
-
Марголис А.А., Рубцов В.В. Учитель для новой школы: модернизация педагогического образования в России // Образовательная политика. — 2010. — № 4 (42).
-
Моро М.И., Волкова С.И, Степанова С.В. Математика. 1 класс: Учебник для общеобразовательных школ. — Ч. 1. — М., 2009.
-
Поливанова К.Н. Действие моделирования как способ диагностики контроля // Диагностика учебной деятельности и интеллектуального развития детей: Сб. научн. тр. — М.: Издание НИИ общей педагогики, 1981. — С. 40—48.
-
Рубцов В.В., Марголис А.А., Гуружапов В.А. О деятельностном содержании психолого-педагогической подготовки современного учителя для новой школы // Культурно-историческая психология. — 2010. — №4.
-
Салмина Н. Г. Знак и символ в обучении. — М., 1988.
-
Федеральный государственный образовательный стандарт высшего профессионального образования по направлению «Психолого-педагогическое образование» (050400), МОН РФ. — М., 2010.
-
Федеральный государственный образовательный стандарт общего (начального) образования, МОН РФ. — М., 2009.
-
Чудинова Е. В. Работа с гипотезами детей в системе Д.Б. Эльконина — В.В. Давыдова // Вопросы психологии. — 1998. — №5.
-
Щедровицкий Г. П. Система педагогических исследований (методологический анализ) // Педагогика и логика. — М., 1993.
Информация об авторах
Метрики
Просмотров
Всего: 717
В прошлом месяце: 9
В текущем месяце: 3
Скачиваний
Всего: 444
В прошлом месяце: 13
В текущем месяце: 5