Вероятностный метод фильтрации артефактов при адаптивном тестировании ¹⁰⁴⁸

1. Введение

Компьютерное тестирование в настоящее время широко используется в медицине, психологии и образовании с целью диагностики, определения уровня компетенций и пригодности испытуемых для выполнения тех или иных функций, включая контроль качества обучения. Качество тестирования и достоверность его результатов в значительной степени зависят от технологий проведения тестов, которые в последние десятилетия стали предметом активных научных исследований.

В первое время тесты строились на основе классической модели тестирования (Карданова, 2008; Тюменева, 2007; Gregory, 2007; Gulliksen, 1950), в основе которой лежит теория погрешности измерений, заимствованная из физики: полагалось, что измеряемые характеристики имеют некоторые «истинные» значения, искажаемые случайными и систематическими погрешностями. Этот подход получил определенное распространение, однако его практическому применению препятствует ряд существенных недостатков:

-возникают проблемы при сравнении сходных особенностей тестируемых, выявленных с помощью разных методик;

-не решается проблема валидности;

-тестовые баллы становятся недостаточно надежными в областях экстремальных значений;

-технология в целом недостаточно надежна и универсальна.

Для преодоления указанных проблем была разработана новая технология тестирования, основанная на латентно-структурном анализе и названная теорией ответов на вопросы (Item Response Theory – IRT)¹ (Тюменева, 2007; Baker, 2001). В ней реализована концепция адаптивного тестирования, согласно которой тестируемому с определенной текущей расчетной оценкой уровня знаний или способностей на каждом шаге тестирования вычисляются и предлагаются задания определенной сложности. Основная концепция новой теории, предложенная Г. Рашем в 1960 году (Rasch, 1980), предполагает, что вероятность правильного ответа на задание определяется разностью уровня знаний или способностей и трудности теста. В зависимости от условий прикладной задачи на практике используются и другие, более сложные модели, построенные на базе данной концепции (Аванесов, 2003; Rasch, 1980; Wright, Stone, 1979; Wright, Masters, 1982).

¹ В русскоязычной литературе также используются и другие варианты ее названия: стохастическая теория тестов, математическая теория измерений, современная теория тестирования, теория латентных черт, теория характеристических кривых заданий, теория моделирования и параметризации педагогических тестов и т. д.

При применении технологии IRT возникают следующие проблемы:

-«статичность» оценок: игнорирование того факта, что результат тестирования вследствие усталости испытуемых и других факторов может, вообще говоря, существенно изменяться со временем, принимая различные значения в процессе сеанса тестирования;

-невозможность учета времени, затрачиваемого на решение тестовых задач, при построении расчетных оценок;

-необходимость выполнения достаточно большого числа заданий для получения оценок с приемлемой точностью;

-сложность вычисления распределения вероятностей возможных результатов теста, что необходимо для оценки их надежности;

-сравнительно сложная для практической реализации процедура оценки точности результата, связанная с применением метода максимального правдоподобия и расчетом доверительных интервалов.

Указанные проблемы делают актуальной разработку новых технологий тестирования. В этой работе рассматриваются новые аспекты применения разработанного ранее авторами подхода к адаптивному тестированию (Куравский, Баранов, 2001, 2002; Куравский и др., 2005; Куравский и др., 2003; Куравский и др., 2010; Куравский и др., 2011; Куравский, Юрьев, 2011 а; Куравский, Юрьев, 2011 б; Kuravsky, Malykh, 2004; Kuravsky, Baranov, 2003, 2004, 2005; Kuravsky et al., 2010; Kuravsky et al., 2011), построенного на использовании обучаемых структур в форме марковских моделей с дискретным и непрерывным временем. Его особенностями, обеспечивающими преимущества перед аналогичными способами тестирования, являются:

-выявление и использование при построении расчетных оценок временной динамики изменения способности справляться с заданиями теста;

-возможность учета при построении расчетных оценок времени, затрачиваемого на решение тестовых задач;

-возможность исследования временной динамики знаний или способностей как в дискретной, так и в непрерывной временной шкале;

-меньшее по сравнению с другими подходами количество заданий, которые следует предъявлять испытуемому для получения оценок знаний или способностей с заданной точностью, что ускоряет процесс тестирования;

-получение распределения вероятностей возможных результатов теста в качестве конечного результата;

-развитая техника идентификации параметров моделей.

Одной из наиболее серьезных проблем, возникающих в процессе тестирования, является появление в истории ответов испытуемого искажающих результаты артефактов, обусловленных подсказками, угадыванием и другими формами некорректного целенаправленного вмешательства в процедуру испытаний. Представленная выше технология адаптивного тестирования позволяет бороться с этими явлениями, устраняя артефакты на основе сравнения наблюдаемых и прогнозируемых результатов ответов на вопросы для разных уровней способностей испытуемых. В качестве инструмента для сопоставления в данной работе предлагается использовать фильтр Калмана (Тихонов и др., 2009; Шахтарин, 2010) – нестационарную систему с обратной связью, включающую в себя как составную часть формирующий фильтр, воспроизводящий идеализированную модель поведения.

Выбор фильтра Калмана для устранения артефактов тестирования среди близких по содержанию подходов является оптимальным решением, поскольку он наилучшим образом согласуется с принятой концепцией адаптивного тестирования и контекстом ее использования. В частности, этот фильтр:

-в отличие от фильтра Винера способен обрабатывать текущую информацию об ответах испытуемого в реальном времени, формируя свои оценки сразу же после получения очередного ответа и не требуя полного протокола тестирования, который недоступен до завершения всей процедуры ответов на вопросы;

-в отличие от фильтра Стратоновича использует только линейные методы оценки, наилучшим образом согласующиеся с применяемой линейной дифференциальной моделью адаптивного тестирования, и не приводит к неоправданному усложнению процесса решения;

-в отличие от фильтра Льюинбергера учитывает ошибки наблюдений и обеспечивает оптимальные оценки.

Далее кратко представлен новый подход к адаптивному тестированию, основанный на использовании марковских моделей, поставлена задача фильтрации артефактов с помощью фильтра Калмана и рассмотрены особенности ее решения.

2. Марковские модели адаптивного тестирования

2.1. Структура и математическое описание применяемых марковских моделей с непрерывным временем. Процедура оценки знаний или способностей

Оценка вероятностей различных уровней способностей проводится по результатам тестирования с использованием параметрических математических моделей, описывающихся марковскими случайными процессами с дискретными состояниями и непрерывным и дискретным временем (Овчаров, 1969; Саати, 2010). Дальнейшее изложение относится только к моделям с непрерывным временем. Непосредственно наблюдаемой величиной является трудность выполняемого теста, измеряемая в логитах. Допустимый диапазон значений этой величины делится на несколько интервалов, каждый из которых рассматривается как отдельное состояние x_i, i=0,1,…,n, в котором тестируемый может находиться с некоторой вероятностью, переходя из одного состояния в другое по определенным правилам. Длина указанных интервалов определяет разрешающую способность оценок, получаемых в процессе тестирования. В свою очередь, число состояний определяется желаемой разрешающей спообностью оценок и доступным объемом выборки ².

² Рассматривая непрерывно изменяющуюся характеристику как дискретную величину, мы теряем часть информации (это имеет место при любой идеализации). Однако эти потери несущественны в случае достаточно больших выборок, когда мы имеем возможность устанавливать длину интервалов состояний так, чтобы она не превышала ошибок измерений.

Как трудности заданий, так и способности тестируемых измеряются в единой безразмерной шкале логитов, выражающей соотношение долей правильных и неправильных ответов. Перевод в шкалу логитов осуществляется по формуле:

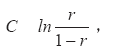
где С – значение в шкале логитов, r – вероятность правильного выполнения задания. В случае оценки трудности этот параметр характеризует возможность выполнения определенного задания для всего множества тестируемых, а в случае оценки способностей – результаты определенного тестируемого для всего множества допустимых заданий. Статистические приближения указанных величин получаются после замены в приведенной формуле вероятности r на ее выборочные оценки.

Если обозначить верхнюю и нижнюю границы диапазона возможных значений трудности тестов как D_bot и D_top, состояние x₀ будет соответствовать интервалу от D_bot до D_bot+(D–_topD_bot)/(n+1), состояние x₁ – интервалу от D_bot+(D_top–D_bot)/(n+1) до D_bot+2(D_top–D_bot)/(n+1) и т. д.

Модели для описания динамики этих переходов представляются ориентированными графами, в которых вершины³ соответствуют состояниям, а дуги⁴ соответствуют переходам.

В случае моделей с непрерывным временем процесс тестирования может рассматриваться как случайное блуждание по графу с переходами из одного состояния в другое согласно направлениям дуг. Эти переходы мгновенны и происходят в случайные моменты времени.

Предполагается, что для них выполняются следующие два свойства пуассоновских потоков событий:

-ординарность (поток называется ординарным, если вероятность появления двух и более событий в течение малого интервала времени намного меньше, чем вероятность появления за это же время одного события);

- независимость приращений (это свойство означает, что количества событий, попадающих в два непересекающихся интервала, не зависят друг от друга).

Можно показать, что в рассматриваемых потоках число событий X, попадающих в любой временной интервал длины t, начинающийся в момент t, распределено согласно закону Пуассона:

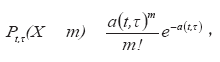
где P_t,t (X = m) – вероятность появления m событий в течение рассматриваемого интервала, a(t,t) – среднее число событий, попадающих в интервал длины t, начинающийся в момент времени t. Далее будут рассматриваться только стационарные потоки (в которых a(t,t)=ht, h=const). Параметр h называется интенсивностью стационарного потока. Он равен среднему числу событий в единицу времени. Средняя продолжительность времени между двумя смежными событиями в этом случае равна 1/h.

³ Обозначаются как прямоугольники. ⁴ Обозначаются как стрелки.

Упомянутые выше предположения о свойствах потоков событий обычны для прикладных задач, так как эти потоки (или потоки, близкие к ним по свойствам) часто встречаются на практике благодаря предельным теоремам для потоков событий (Овчаров, 1969; Саати, 2010).

Для моделей с непрерывным временем неизвестными (свободными) параметрами модели являются интенсивности потоков событий. Их значения определяются путем сравнения наблюдаемых и прогнозируемых гистограмм, описывающих распределения частот пребывания в состояниях модели, а именно: вычисляются значения, обеспечивающие наилучшее соответствие наблюдаемых и ожидаемых частот попадания в определенное состояние системы в заданные моменты времени. Прогнозируемые вероятности нахождения в состояниях получаются путем численного интегрирования систем уравнений Колмогорова.

Марковские модели с непрерывным временем и свободными параметрами, которые идентифицируются по данным наблюдений, называются сетями Маркова (Куравский, Баранов, 2002; Куравский и др., 2003; Kuravsky, Baranov, 2003, 2004, 2005).

Для описания того, как вероятности нахождения в заданных состояниях изменяются со временем, применяются сети Маркова, организованные по так называемой схеме «гибели и размножения» ⁵ (рис. 1). Эта схема представляет собой конечную цепь из n+1 состояния, в которой переходы из состояния x_k (k¹0, k¹n) возможны только в предшествующее состояние x или в следующее по порядку состояние x. Из состояний x и x доступны только состояния x₁ и x_n-1, соответственно.

Рис. 1. Сеть Маркова, представляющая процесс тестирования с непрерывным временем: xi (i=0,1,…,n) – состояния, li (i=0,1,…,n-1) и mi (i=1,2,…,n) – интенсивности переходов

Динамика вероятностей нахождения в различных состояниях указанной схемы описывается следующей системой обыкновенных дифференциальных уравнений Колмогорова:

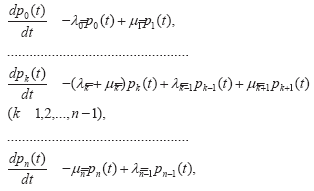
где p_*(t) есть вероятность нахождения в состоянии x_* в момент времени t; _* – номер состояния; l_i (i=0,1,…,n-1) и m_i (i=1,2,…,n) – интенсивности переходов между состояниями, которые определяются отдельно для каждого из рассматриваемых уровней способностей. Для интегрирования указанной системы необходимо задать начальные условия: p₀(0), p₁(0),…, n p_n(0). Нормализующее условие Σk=0 ()t =1 выполняется в любой момент времени. 

⁵ Она была впервые применена в биологии для анализа динамики роста популяций.

Для упрощения задачи, а также для обеспечения приемлемой процедуры идентификации интенсивности потоков часто полагаются зависящими от индекса i по определенным правилам, включая тривиальный вариант: l₀=l₁=…=l_n-1=l и m₁=m₂=…=m_n=m. Оптимальный выбор подобных зависимостей опирается на технику проверки статистических гипотез. В случае моделей с дискретным временем аналогичные зависимости исследуются для вероятностей переходов.

Процедура адаптивного тестирования заключается в последовательном предъявлении испытуемому задач, трудность которых определяется состоянием сети или цепи Маркова, в котором он находится в данный момент. Если испытуемый, находясь в состоянии x_i, решает задачу, он переходит в состояние x_i+1, в противном случае – в состояние x_i-1. По завершении тестирования он оказывается в одном из состояний x_*, наилучшим образом соответствующих его уровню способностей. Принцип выбора очередного теста заключается в выборе задачи, трудность которой примерно соответствует уровню способностей испытуемого. Согласно проведенным наблюдениям и результатам современной теории тестирования, это обеспечивает наилучшую дифференциацию испытуемых по уровню их способностей.

2.2. Идентификация марковских моделей с непрерывным временем

Идентификации марковских моделей проводятся по выборкам испытуемых, отдельно для каждого из рассматриваемых уровней способностей. Каждому уровню способностей C_i, i=1,…,I при этом ставится в соответствие свой уникальный набор оценок параметров модели, что позволяет в дальнейшем выявлять значение этого показателя, наилучшим образом согласующегося с наблюдениями. Таким образом, вероятности и интенсивности переходов являются функциями двух характеристик: уровня способностей и трудности задачи. Число уровней способностей – это дискретный параметр, который задает разрешающую способность оценки данной характеристики и устанавливается при решении каждой прикладной задачи в зависимости от объема выборки испытуемых, имеющейся у исследователя при решении задачи идентификации, и желаемой точности результата.

С каждой изменяющейся со временем гистограммой пребывания в состояниях модели связывается марковский процесс с дискретными состояниями. Статистика Пирсона

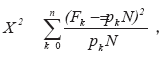
где N – число элементов в выборке, p_k – прогнозируемая вероятность попадания в k-е состояние модели, а F_k – наблюдаемая частота нахождения в k-м состоянии модели, используется как мера соответствия в том смысле, что ее большие значения означают плохое согласование прогнозируемых и наблюдаемых результатов, а малые значения – хорошее согласование. Для идентификации модели минимизируется сумма указанных статистик в те моменты времени, для которых имеются результаты наблюдений. Наблюдаемые количества попаданий в различные интервалы трудностей задач определяются по результатам тестирования группы испытуемых. В качестве искомых оценок свободных параметров моделей используются значения, обеспечивающие наилучшее соответствие наблюдаемых и прогнозируемых частот попадания в определенное состояние системы в заданные моменты времени.

Доказано, что при выполнении ряда общих условий значения статистики Пирсона X² , получаемые при подстановке истинных решений, асимптотически описываются распределением c² с n–l степенями свободы, где l – число определяемых параметров, причем вычисленные значения свободных параметров при увеличении объема выборки сходятся по вероятности к искомому решению (Крамер, 1976). Это позволяет использовать приведенную статистику для проверки гипотезы о том, что полученный прогноз согласуется с результатами наблюдений. Данный способ идентификации свободных параметров называется методом минимума c² (Крамер, 1976) и дает решения, близкие к полученным, методом максимального правдоподобия.

Используемая процедура вычисления оцениваемых параметров состоит из двух этапов. На подготовительном этапе с помощью электронной таблицы для указанной системы дифференциальных уравнений кодируется численная схема интегрирования, позволяющая вычислять вероятностные функции p_k (Куравский, Баранов, 2002; Куравский и др., 2003; Kuravsky, Baranov, 2003). Эти функции вычисляются с некоторым заданным временным шагом. Для вычисления решения с приемлемой точностью оказались достаточными методы Рунге-Кутта или их эквиваленты.

На заключительном этапе запускается численная процедура многомерной нелинейной оптимизации ⁶ (Куравский, Баранов, 2002; Куравский и др., 2003; Kuravsky, Baranov, 2003), позволяющая получать искомые значения свободных параметров. Полученные оценки свободных параметров рассматриваются как характеристики модели, выявленные в результате наблюдений. Рассмотренный критерий также позволяет сравнивать между собой различные варианты марковских моделей, выбирая среди них оптимальные.

2.3. Поиск оптимального решения

Зная состояние модели, в котором оказался тестируемый после решения последней предложенной ему задачи, и рассчитав вероятность нахождения в этом состоянии в заданный момент времени для каждого из рассматриваемых уровней способностей с помощью дифференциальных зависимостей (см. раздел 2.1), можно оценить вероятности пребывания в указанном конечном состоянии по формуле Байеса:

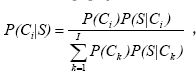
где С_i – событие, связанное с наличием у тестируемого i-го уровня способностей (i=1,…,I), S – событие, связанное с нахождением в заданном конечном состоянии модели в заданный момент времени, P(C_i) – априорная вероятность появления i-го уровня способностей у тестируемого, P(S|C_i) – вероятность нахождения в заданном конечном состоянии модели в заданный момент времени при наличии i-го уровня способностей, P(C_i|S) – вероятность i-го уровня способностей при условии нахождения в заданном конечном состоянии модели в заданный момент времени.

Уровень способностей, при котором достигается наибольшая условная вероятность

P(C_max|S) = max{P(C_i|S)}_i=1,...,I , дает искомую оценку. Распределение вероятностей {P(C_i|S)} , которое является результатом решения задачи, позволяет оценить степень надежности этой оценки.

⁶ В настоящее время предлагается достаточно много программных продуктов для решения задач численной оптимизации. В частности, пользователи электронной таблицы Excel могут применять программное обеспечение компании Frontline Systems, Inc.

Как указано в разделе 2.1, разрешающая способность полученной оценки определяется длиной интервала между соответствующими смежными уровнями способностей в логитах, которая, в свою очередь, при условии постоянства таких длин задается числом уровней способностей I.

3. Математическая постановка и решение задачи фильтрации Калмана при адаптивном тестировании с использованием марковских моделей

В случае обсуждаемого варианта адаптивного тестирования наблюдаемый процесс представляет историю пребывания в состояниях марковских моделей. Он выражается вектором x(t)=(x₀(t),x₁(t),…,x_n(t))^T, в котором в каждый момент времени один, и только один, из компонентов x_i(t), i=0,…,n, соответствующий состоянию, где находится испытуемый, равен единице, а остальные компоненты равны нулю. В свою очередь, исследуемый информационный процесс P(t)=(p₀(t),p₁(t),…,p_n(t))^T представляет динамику изменения вероятностей пребывания в состояниях модели.

Уравнения информационного и наблюдаемого процессов, используемые при построении многомерного непрерывного фильтра Калмана для моделей рассматриваемого типа ⁷ dt имеют следующий вид (Тихонов и др., 2009; Шахтарин, 2010):

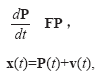
где на случайные ошибки наблюдений Е(v(t)) накладываются условия E(v(t))=0 и E(v(t)v^T(t))=Rd(t–t), матрица формирующего фильтра F размерности (n+1)´(n+1) есть

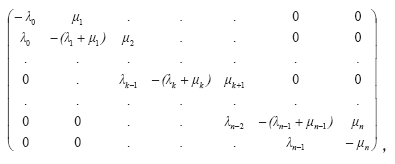
а R – симметричная положительно определенная матрица, которую мы далее будем полагать не зависящей от времени. При проведении практических расчетов эта матрица может заменяться на одну их своих выборочных оценок R^ˆ , полученных для каждого из рассматриваемых уровней способностей на основе результатов наблюдений.

Дифференциальное уравнение фильтра Калмана, определяющее несмещенную оценку исследуемого процесса ⁸ Pˆ ()t )= (pˆ ()t , pˆ ()t ,..., pˆ ()t ) с минимальным средним квадратом ошибки e(t)=P(t)– , представляется в виде:

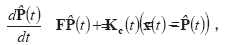где K(t) – матричный коэффициент усиления фильтра Калмана.

⁷ Особенностями этих моделей являются: отсутствие информационного шума, равенство размерностей информационного процесса и процесса наблюдений и единичная матрица наблюдений.

⁸ Выход фильтра Калмана.

В классическом случае этот коэффициент задается уравнением:

K_c(t)=U(t)R^-1,

в котором ковариационная матрица ошибок U(t)=E(e(t)e^T(t)) является решением одной из матричных форм уравнения Риккати:

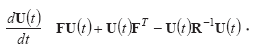
Однако, поскольку в рассматриваемой задаче компоненты оценки информационного процесса Pˆ ()t представляют собой нормированные величины – вероятности пребывания в состояниях сети Маркова c суммой, равной единице, – необходима коррекция коэффициента усиления K_c(t), обеспечивающая поддержание данного условия.

Если нормализующее условие _å ⁿpˆ _k ()t =1 выполняется в начальный момент времени k=0  t=0, а правая часть уравнения фильтра Калмана такова, что при t³0 обеспечивается равенство, то указанное нормализующее условие выполняется в любой момент времени t³0. Очевидно, что условие ¦ _dt^{k 0} равносильно равенству нулю суммы компонентов вектора, заданного матричным выражением ˆ () K t (-Pˆ ()t ). Поскольку нулевая сумма компонентов вектора FPˆ ()t обеспечивается приведенной выше структурой матрицы F, то для равенства нулю суммы компонентов всего указанного матричного выражения необходимо и достаточно нулевой суммы компонентов вектора K_c () () (x t P()t ).

Сумма компонентов вектора x()t -Pˆ()t равна нулю по условиям рассматриваемой задачи, так как эти величины интерпретируются как вероятности. Учитывая данный факт, несложно доказать, что достаточным условием нулевой суммы компонентов вектора

K_c () () t (x t -Pˆ()t )является равенство сумм элементов матрицы K_c (t) во всех ее столбцах. Таким образом, если матричный коэффициент усиления K_c(t) в уравнении фильтра Калмана заменить на близкий к нему нормализованный коэффициент K_n(t) с равными во всех столбцах суммами элементов, то условие dpˆ t будет выполнено. Матрицу K (t) можно получить, домножив справа матрицу K_c(t) на диагональную матрицу D, элементы которой вычисляются по формуле:

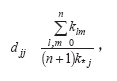где d_jj – j-й диагональный элемент матрицы D; k_lm, l,m=0,…,n – элементы матрицы K (t); k– сумма элементов в j-м столбце матрицы K (t). Такая замена корректна, если K_n(t)=U(t)R^-1D лежит в допустимых границах вариаций коэффициента K_c(t), обусловленных ошибками выборочных оценок матрицы R, что проверяется с помощью подходящих критериев согласия.

В частности, для этого можно:

-сгенерировать множество выборочных оценок ковариационной матрицы R, соответствующих доверительным интервалам для заданного объема выборки N;

-вычислить, используя эти оценки, выборку матриц {K(t)}; nii=1,..,M

-вычислить выборочное распределение евклидовой нормы разностей классического и нормированного коэффициентов усиления;

-учитывая, что полученное выборочное распределение при достаточно большом числе элементов в матричных коэффициентах усиления приблизительно соответствует нормальному, построить для него выборочные оценки математического ожидания и дисперсии и оценить вероятность p превышения евклидовой нормы разности

K_n ()t -K_c ()t.

Если p³0,05, то использование нормализованного коэффициента K_n(t) является допустимым. Рассмотренный метод может быть совмещен с процедурой кластеризации, использующей самоорганизующиеся карты Кохонена (Куравский и др., 2011; Kuravsky et al., 2011).

В соответствии с представленной выше процедурой адаптивного тестирования, фильтрация Калмана выполняется автономно для каждого из уровней способностей, учитываемых при постановке решаемой задачи.

В заключение следует отметить, что существует ряд интересных аналогий между фильтром Калмана и скрытыми марковскими моделями (Куравский и др., 2010; Kuravsky et al., 2010), частично рассмотренных в обзорах зарубежных авторов (см., напр.: Roweis, Ghahramani, 1999).

4. Программная реализация

Рассмотренная процедура фильтрации реализована в среде графического программирования LabVIEW (см. рис. 2). При этом интегрирование матричного уравнения Риккати и уравнения фильтра Калмана выполнено численными методами ⁹, а для оценки начального состояния ковариационной матрицы ошибок U(0), о которой наблюдения дают, как правило, мало полезной информации, использованы следующие предположения:

-E(e(0))=0;

-компоненты вектора ошибок фильтрации e(0) статистически независимы;

-дисперсии компонентов вектора ошибок фильтрации e(0) пропорциональны соответствующим дисперсиям компонентов случайного шума наблюдения v(t).

5. Основные результаты и выводы

1.      Разработан и программно реализован вероятностный метод фильтрации искажающих результаты артефактов при адаптивном тестировании, построенном на использовании обучаемых структур в форме марковских моделей с непрерывным временем.

2.      Устранение артефактов, обусловленных различными формами некорректного целенаправленного вмешательства в процедуру испытаний, выполняется на основе сравнения наблюдаемых и прогнозируемых результатов ответов на вопросы для разных уровней способностей испытуемых с помощью фильтра Калмана, адаптированного для задачи адаптивного тестирования.

3. Выбор фильтра Калмана для устранения артефактов является оптимальным среди близких по содержанию подходов, поскольку он наилучшим образом согласуется с принятой концепцией адаптивного тестирования и контекстом ее использования.

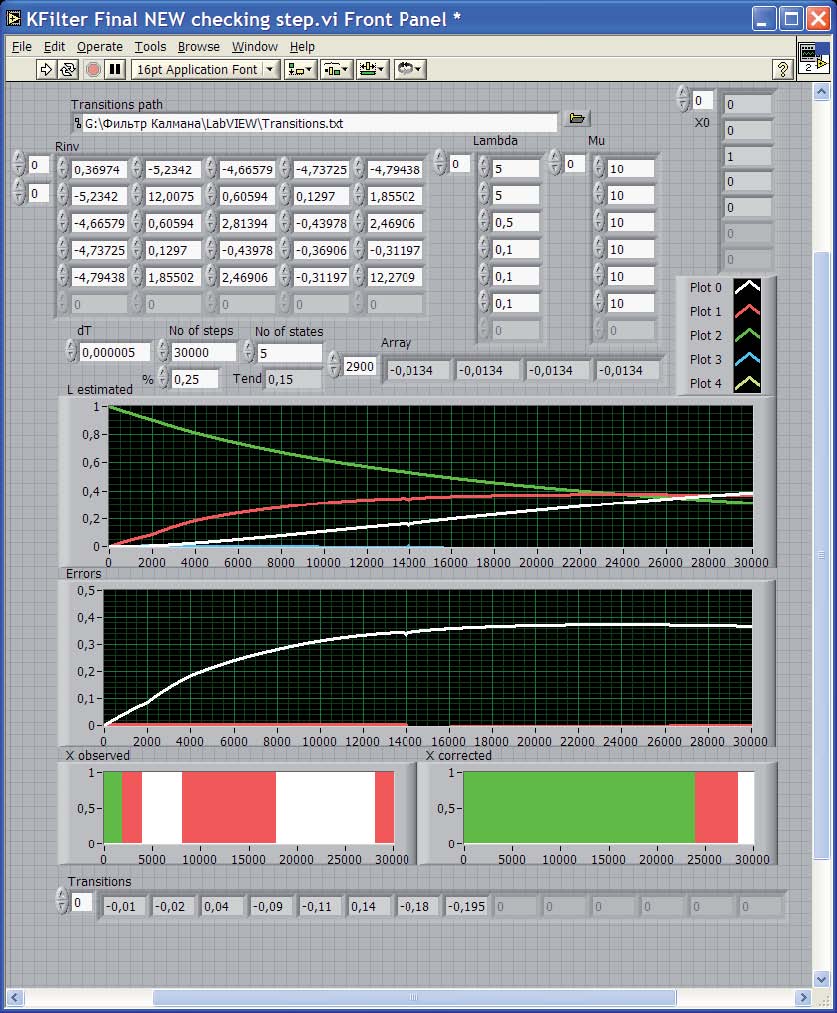
Рис. 2. Результаты фильтрации Калмана для марковской модели с пятью состояниями