Моделирование и анализ данных
2012. Том 2. № 1. С. 92–96
ISSN: 2219-3758 / 2311-9454 (online)
Canonical ensemble of open strings
Аннотация
Общая информация
Ключевые слова: Open string, canonical ensemble, entropy
Рубрика издания: Научная жизнь
Тип материала: научная статья
Для цитаты: Алхимов В.И. Canonical ensemble of open strings // Моделирование и анализ данных. 2012. Том 2. № 1. С. 92–96.
Полный текст

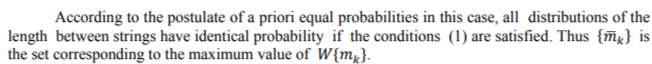






The result obtained can be used as a purely theoretical study of various systems as well as in technical applications. In particular, by using the formula (13), the entropy of nanostructures can be determined, thereby their thermodynamics in condition monitoring is established. This result allows to establish criterion for the strength of chain systems, depending on the physical state of their environment.
Литература
- Alkhimov V.I., “Configuration statistics of the open string d-dimensional model”, Modelling and data analysis, 2011, No 1, pp 41 -54 (in Russian).
- Huang K., “Statistical mechanics”, John Wiley & Sons, Inc.: N.Y.–London, 1963.
- Bateman H., Erdelyi A., “Higher transcendental functions”, Vol 2, Mc Graw-Hill Book Comp. Inc.: N.Y.–London, 1953.
Информация об авторах
Метрики
Просмотров
Всего: 793
В прошлом месяце: 2
В текущем месяце: 1
Скачиваний
Всего: 389
В прошлом месяце: 0
В текущем месяце: 0