Моделирование и анализ данных
2014. Том 4. № 1. С. 129–138
ISSN: 2219-3758 / 2311-9454 (online)
Численные решения задачи на собственные значения для обыкновенных дифференциальных уравнений второго порядка с особыми точками
Аннотация
Общая информация
Ключевые слова: Численные методы, обыкновенные дифференциальные уравнения, особые точки, задача на собственные значения, кулоновский потенциал, потенциал с жёсткой сердцевиной
Рубрика издания: Численные методы
Тип материала: научная статья
Для цитаты: Полупанов А.Ф. Численные решения задачи на собственные значения для обыкновенных дифференциальных уравнений второго порядка с особыми точками // Моделирование и анализ данных. 2014. Том 4. № 1. С. 129–138.
Полный текст
1. ВВЕДЕНИЕ
Мы рассматриваем следующее радиальное уравнение Шредингера для кулоновских состояний
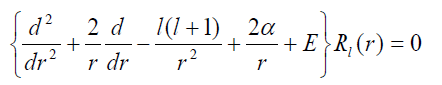 (1)
(1)
где r > 0 - радиальная переменная, l - неотрицательное целое (квантовое число орбитального углового момента), а - целое (а = 1 соответствует кулоновскому притяжению в атоме водорода), Rl (r) - кулоновская радиальная волновая функция, E -энергия. В общем случае, расстояния и энергия измеряются в единицах ![]() (эффективный боровский радиус) и
(эффективный боровский радиус) и ![]() (эффективный ридберг), соответственно, где e - заряд электрона, m - эффективная масса электрона, или приведённая масса - в случае относительного движения двух притягивающихся частиц (экситон), к - статическая диэлектрическая проницаемость.
(эффективный ридберг), соответственно, где e - заряд электрона, m - эффективная масса электрона, или приведённая масса - в случае относительного движения двух притягивающихся частиц (экситон), к - статическая диэлектрическая проницаемость.
Уравнение (1) имеет две особые точки: регулярную особенность при r = 0 и иррегулярную особенность при r =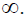
Уравнение (1) описывает кулоновские состояния атома водорода и водородоподобного атома в различных системах, например, состояния мелких донорных примесей в объёмных прямозонных полупроводниках или в полупроводниковых квантовых точках. В настоящей работе рассматривается задача на собственные значения и связанные с ней проблемы для уравнения (1). Энергии и волновые функции нескольких нижайших дискретных состояний вычисляются как в случае, когда известны точные аналитические решения задачи (см., например, [1,2]), что позволяет оценить точность расчётов, так и в задачах, решение которых возможны только с применением численных методов. Рассматривается задача о связанных состояниях водородоподобного атома в квантовой точке, о волновой функции основного состояния водородоподобных атомов в модели центрально-ячеечного потенциала нулевого радиуса [3,4], о связанных состояниях водородоподобного атома в модели кулоновского потенциала с жёсткой сердцевиной. Для решения этих проблем используются явные численноаналитические методы, основанные на методе рекуррентных последовательностей [5, 6, 7].
Подстановка 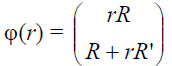 сводит (1) к системе двух уравнений первого порядка:
сводит (1) к системе двух уравнений первого порядка:
![]() (2)
(2)
где ![]()
![]()
Ясно (по определению, см. [8]), что точка r = 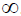 есть регулярная особая точка для уравнения (1), а r = от - иррегулярная особенность (замена переменной z = 1/r). Методы построения решений уравнения (3), решения сингулярной задачи на собственные значения и задачи рассеяния для (3) развиты в [6,7] в общем случае, т.е. когда A(r) - это произвольная голоморфная в окрестности r = 0 n х n матричная функция, а
есть регулярная особая точка для уравнения (1), а r = от - иррегулярная особенность (замена переменной z = 1/r). Методы построения решений уравнения (3), решения сингулярной задачи на собственные значения и задачи рассеяния для (3) развиты в [6,7] в общем случае, т.е. когда A(r) - это произвольная голоморфная в окрестности r = 0 n х n матричная функция, а ![]() (r) - n-мерный столбец. В данной работе рассматриваются решения уравнения, представленного в виде ОДУ второго порядка (1) (см. [5]).
(r) - n-мерный столбец. В данной работе рассматриваются решения уравнения, представленного в виде ОДУ второго порядка (1) (см. [5]).
2. ФУНДАМЕНТАЛЬНАЯ СИСТЕМА РЕШЕНИЙ
2.1. Окрестность регулярной особенности r = 0
Регулярное решение (1) имеет вид степенного ряда
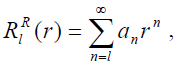 (3)
(3)
Где коэффициенты an удовлетворяют следующему рекуррентному соотношению
![]() (4)
(4)
Ясно, что коэффициент al есть произвольная константа C, которая определяется нормировкой. Выражение для производной решения получается непосредственным дифференцированием (3).
Второе, иррегулярное решение (1) имеет вид алгебраической комбинации степенных рядов и логарифмической функции:
![]() (5)
(5)
Здесь ![]() (r) - это решение (3), (4) с коэффициентом al, определяемым равенством
(r) - это решение (3), (4) с коэффициентом al, определяемым равенством
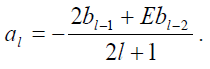
Коэффициенты bn удовлетворяют следующему рекуррентному соотношению
![]() (6)
(6)
Следует отметить, что, как следует из [6, Теорема 4] формальные степенные ряды в (3), (5) сходятся при r <
2.2. Окрестность иррегулярной особенности r = ∞
При построении асимптотических разложений решений в окрестности иррегулярной особенности r = ∞, будем следовать методу [5,9] (а не [7]). Подстановка ![]() в (1) приводит его к виду
в (1) приводит его к виду
![]() (7)
(7)
В свою очередь, подстановка
![]() (8)
(8)
сводит (7) к следующему уравнению для функции 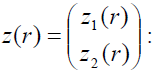
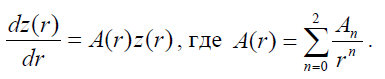 (9)
(9)
A(r) - 2×2 матричная функция с диагональным матричным коэффициентом A0:
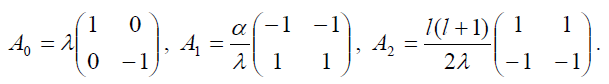 (10)
(10)
Для нахождения асимптотического разложения решений (8) при at r →∞ сделаем подстановку
z(r) = P (r)ω(r), (11)
где матричная функция P (r) есть асимптотический ряд по обратным степеням r
![]()
причём полагаем, что P0 - единичная матрица, те. ![]() . Подчиним матрицу P(r) такому требованию, чтобы функция ω(r) была решением уравнения
. Подчиним матрицу P(r) такому требованию, чтобы функция ω(r) была решением уравнения
![]() (12)
(12)
где B(r) - диагональная матричная функция: ![]() которая также есть асимптотический ряд по
которая также есть асимптотический ряд по ![]() Матрицы Pn и Bn удовлетворяют следующим рекуррентным соотношениям
Матрицы Pn и Bn удовлетворяют следующим рекуррентным соотношениям
![]() (13)
(13)
Поскольку при нашем выборе матрицы B0 выполняется равенство
![]()
имеем: ![]() (14)
(14)
где
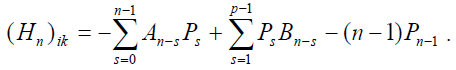 (15)
(15)
и произвол в выборе диагональных элементов матриц ![]() . Для определённости мы их полагаем равными нулю:
. Для определённости мы их полагаем равными нулю:
![]() (16)
(16)
При![]() получаем из (13):
получаем из (13):
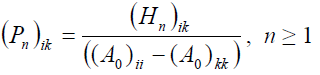 (17)
(17)
Интегрирование уравнения (12) с диагональной матрицей B даёт:
![]() (18)
(18)
где Ci - произвольные константы, что приводит к следующему выражению для асимптотического разложения решений уравнения (9):
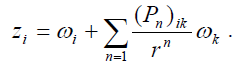 (19)
(19)
Следует отметить, что равенства (18), (19) дают выражение для асимптотического разложения решений (9) при r → ∞ и в случае произвольного числа уравнений в системе (9). В рассматриваемом случае n=2, E < 0 (состояния дискретного спектра) нас будут интересовать только сходящиеся при r → ∞ решения (7), (1). Соответствующие асимптотические разложения решения ![]() и его
и его
производной ![]() имеют вид
имеют вид
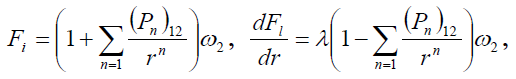 (20)
(20)
где ω2 определяется (18) с произвольной константой C2 и (B0)2 = - λ.
3. СШИВКА РЕШЕНИЙ. ЗАДАЧА НА СОБСТВЕННЫЕ ЗНАЧЕНИЯ
3.1. Стандартный случай
Стандартная задача на собственные значения для уравнения (1) на [0, ∞) состоит в следующем: нужно найти такие значения параметра E: E < 0 (энергии), при которых решения Ri (r) ограничены при r = 0 и Ri (r) → 0 при r → ∞, нужно также найти решения, соответствующие этим собственным значениям E, и нормированные условием:
![]() (21)
(21)
Для решения задачи необходимо в некоторой промежуточной точке r = ȓ сшить регулярное при r = 0 решение ![]() (3) и его производную (lhs - «левое» решение), соответственно, с решением, сходящимся при r → ∞, и его производной (см. (20)) (rhs - «правое» решение). Если обозначить через Ф0( E) столбец, составленный из значений, принимаемых lhs (3) и его производной при ai = 1 (4) в точке r = ȓ при данном E, а - через
(3) и его производную (lhs - «левое» решение), соответственно, с решением, сходящимся при r → ∞, и его производной (см. (20)) (rhs - «правое» решение). Если обозначить через Ф0( E) столбец, составленный из значений, принимаемых lhs (3) и его производной при ai = 1 (4) в точке r = ȓ при данном E, а - через ![]() (E) - столбец из rhs и его производной при С2 = 1, и определить 2х2 матрицу
(E) - столбец из rhs и его производной при С2 = 1, и определить 2х2 матрицу ![]()
то для выполнения сшивки должно выполняться равенство:
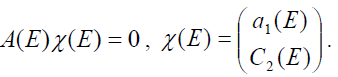 (22)
(22)
Таким образом, процедура вычисления некоторого собственного значения E = E0 сводится к численному решению уравнения
det A(E) = 0 (23)
После определения собственного значения Е0, решая (22) находим связь между компонентами вектора х(Е0), а затем, используя (21), - значения констант (С2Е0) и ai(E0), чем полностью определяем собственную функцию и её производную на [0, ∞).
Следует отметить, что сшивка решений всегда может быть проведена с заданной точностью с помощью правильного выбора точки сшивки ȓ. Формально это можно выразить следующим образом: пусть X = Х(ȓ) обозначает некоторый математический объект, который нужно вычислить (например, энергия, собственная функция), тогда
![]()
При практических вычислениях, для оценки ошибок удобно использовать вариацию точки сшивки ![]()
Для оценки точности вычислений найдены энергии и волновые функции нескольких нижайших связанных состояний атома водорода (а =1) в (1). В этом случае известно точное аналитическое решение задачи [1, 2]. Энергии уровней (собственные значения) равны![]() ... Собственные функции (радиальные волновые функции) двух нижайших состояний с l = 0 имеют вид:
... Собственные функции (радиальные волновые функции) двух нижайших состояний с l = 0 имеют вид: ![]() (здесь первый индекс - главное квантовое число п, второй - l [1, 2]). Вычисленные значения энергий и собственных функций близки к точным с высокой точностью, в частности, для указанных состояний верными являются 14 значащих цифр в собственных значениях и 12 - в собственных функциях (подробное сравнение вычисленных и точных величин см. в разделе 3.2).
(здесь первый индекс - главное квантовое число п, второй - l [1, 2]). Вычисленные значения энергий и собственных функций близки к точным с высокой точностью, в частности, для указанных состояний верными являются 14 значащих цифр в собственных значениях и 12 - в собственных функциях (подробное сравнение вычисленных и точных величин см. в разделе 3.2).
3.2. Задача на собственные значения на конечном отрезке
В данном разделе рассматривается следующая сингулярная задача на собственные значения для уравнения (1) на конечном отрезке![]() : нужно найти такие значения параметра Е, при которых
: нужно найти такие значения параметра Е, при которых ![]() ; нужно также найти решения (1), соответствующие этим собственным значениям Е, и нормированные условием:
; нужно также найти решения (1), соответствующие этим собственным значениям Е, и нормированные условием:
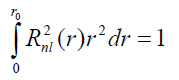 (24)
(24)
Отметим, что к решению такой задачи на собственные значения сводится (в простой модели) задача о состояниях водородоподобного донора, расположенного в центре полупроводниковой сферической квантовой точки (КТ) (полупроводниковый шар малого (~ 10 нм) радиуса в диэлектрической матрице, см., например, [10]).
Задачу на собственные значения в этом случае следует решать численно - аналитическое решение можно найти только при тех значениях r0, когда узел собственной функции задачи на бесконечном полуинтервале совпадает с радиусом КТ [10]. В данном случае, процедура вычисления собственных значений сводится к численному решению уравнения
![]() (25)
(25)
где ![]() - это регулярные при r = 0 решения (3). Для определённости, при вычислениях полагаем al = 1 в (4). После определения некоторого собственного значения Е0, равенства (3) и (4) дают выражения для ненормированного решения. Для получения нормированной собственной функции нужно вычислить интеграл в левой части (24) от полученного решения (назовём его Q), тогда нормированное решение даётся выражениями (3), (4) с
- это регулярные при r = 0 решения (3). Для определённости, при вычислениях полагаем al = 1 в (4). После определения некоторого собственного значения Е0, равенства (3) и (4) дают выражения для ненормированного решения. Для получения нормированной собственной функции нужно вычислить интеграл в левой части (24) от полученного решения (назовём его Q), тогда нормированное решение даётся выражениями (3), (4) с ![]() . Интегрирование в левой части (24) с функцией (3) даёт
. Интегрирование в левой части (24) с функцией (3) даёт
![]() (26)
(26)
В Таблице 1 представлены результаты расчёта зависимости величин трёх наименьших собственных значений E = Enl (индекс n соответствует таковому для задачи на бесконечном полуинтервале 0 ≤ r < ∞) от радиуса КТ г0. Из таблицы, в частности, видно, что индекс n («главное квантовое число») при конечных г0 уже не нумерует состояния: вырождение состояний с n = 2, l = 0,1 снимается.
Таблица 1. Зависимость энергий трёх нижайших кулоновских состояний от г0
|
г0 |
E1,0 |
E2,0 |
E2,1 |
|
от |
-1 |
-0,25 |
-0,25 |
|
15 |
-0,9999999998 |
-0,2490 |
-0,2495 |
|
10 |
-0,999998 |
-0,2256 |
-0,2377 |
|
9 |
-0,999991 |
-0,2057 |
-0,2275 |
|
8 |
-0,99995 |
-0,1695 |
-0,2089 |
|
7 |
-0,9997 |
-0,1025 |
-0.1750 |
|
6 |
-0,9986 |
0,0255 |
-0,1111 |
|
5 |
-0,9928 |
0,2825 |
0,01520 |
|
4 |
-0,9665 |
0,8405 |
0,2871 |
|
3 |
-0,8479 |
2,223 |
0,9625 |
|
2 |
-0,2500 |
6,655 |
3,152 |
|
1,8 |
0,06510 |
8,622 |
4,131 |
|
1,6 |
0,5426 |
11,42 |
5,530 |
|
1,4 |
1,294 |
15,59 |
7,614 |
|
1,2 |
2,539 |
22,12 |
10,89 |
|
1 |
4,748 |
33,14 |
16,45 |
Как отмечено выше, аналитическое решение задачи для конечного отрезка можно найти тогда, когда узел собственной функции задачи на бесконечном полуинтервале совпадает с радиусом КТ. Из Таблицы 1 видно, что при г0 = 2 вычисленное наименьшее собственное значение (энергия основного состояния) есть E10 = -0,25 (с высокой точностью - по крайней мере 14 верных значащих цифр). Этому значению соответствует, в частности, решение ![]() (1) (ему соответствует также решение (1)
(1) (ему соответствует также решение (1) ![]() , которое и имеет узел при r = 2, т.е. это и есть соответствующая собственная функция, нормированная условием (24), если положить
, которое и имеет узел при r = 2, т.е. это и есть соответствующая собственная функция, нормированная условием (24), если положить ![]() . Точность метода можно оценить, в частности, сравнивая значение величины Q, вычисленное с помощью выражения (26): Q= 0.105306034687423 и с помощью точной формулы Q = 2 - 14e-2 =0.105306034687422. Сравнение точных и найденных с помощью описанного метода значений собственной функции показывает совпадение 14 значащих цифр в этих величинах при всех г: 0 ≤ r ≤ 2.
. Точность метода можно оценить, в частности, сравнивая значение величины Q, вычисленное с помощью выражения (26): Q= 0.105306034687423 и с помощью точной формулы Q = 2 - 14e-2 =0.105306034687422. Сравнение точных и найденных с помощью описанного метода значений собственной функции показывает совпадение 14 значащих цифр в этих величинах при всех г: 0 ≤ r ≤ 2.
3.3. Волновая функция основного состояния в модели центральноячеечного потенциала нулевого радиуса
Модель центрально-ячеечного потенциала нулевого радиуса описывает влияние короткодействующего потенциала, создаваемого примесным атомом в полупроводнике (помимо кулоновского потенциала), на основное состояние в кулоновском потенциале [3]. Математически это означает следующее: нужно найти нормируемое условием (21) решение уравнения (1), соответствующее некоторому заданному значению E = Е0 < 0, не равному собственному значению (1). Ясно, что такое решение есть линейная комбинация регулярного (3) и иррегулярного (5) решений
![]() (27)
(27)
при l = 0 (поскольку ![]() (r) ведёт себя в нуле как
(r) ведёт себя в нуле как ![]() ), экспоненциально убывающая на бесконечности. Задача состоит в отыскании константы M при заданном Е0. Для этого нужно провести сшивку решений, т.е. найти нетривиальное решение уравнения (22), в котором матрица A и вектор х есть функции M, а столбец Ф0 = Ф0(M) составлен из значений, принимаемых (27) и его производной
), экспоненциально убывающая на бесконечности. Задача состоит в отыскании константы M при заданном Е0. Для этого нужно провести сшивку решений, т.е. найти нетривиальное решение уравнения (22), в котором матрица A и вектор х есть функции M, а столбец Ф0 = Ф0(M) составлен из значений, принимаемых (27) и его производной ![]() в точке r =ȓ при данном M. Процедура вычисления М при заданном Е0 сводится к численному решению уравнения det A(M) = 0.
в точке r =ȓ при данном M. Процедура вычисления М при заданном Е0 сводится к численному решению уравнения det A(M) = 0.
После определения собственного значения M при данном Е0, решая (22), находим связь между компонентами вектораx (M), а затем, используя (21), - значения констант C2(M) и b-1(M), чем полностью определяем волновую функцию и её производную.
На рис. 1 представлена вычисленная зависимость коэффициента M в линейной комбинации регулярного и иррегулярного решений (1) от энергии Е.
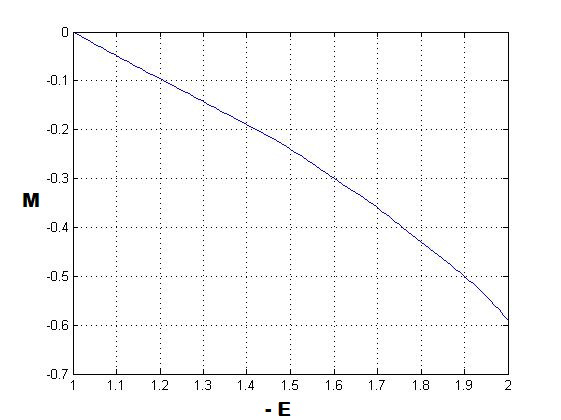
Рис.1. Зависимость коэффициента M в (27) от параметра E (энергии) в (1)
3.4. Задача на собственные значения в случае потенциала с жёсткой сердцевиной и кулоновским «хвостом»
Модели, использующие потенциал с жёсткой сердцевиной (hardcore potential), рассматриваются в различных приложениях, а методы решения задач квантовой механики при его наличии представляют собой самостоятельный интерес [11]. Модель потенциала с жёсткой сердцевиной и кулоновским хвостом может быть полезна для описания слабосвязанных состояний многоэкситонных комплексов, связанных на примеси в полупроводнике.
Рассматривается следующая задача на собственные значения для уравнения (1): нужно найти такие значения параметра Е: Е < 0 (энергии), при которых решение (1) Rl(r) = 0 при г ≤ гнс (гнс - радиус действия потенциала с жёсткой сердцевиной) и Rl (r) → 0 при r → ∞; нужно также найти решения, соответствующие этим собственным значениям Е, и нормированные условием:
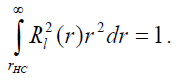 (28)
(28)
Для решения задачи необходимо при каждом значении E в (1) найти такую линейную комбинацию регулярного (3) и иррегулярного (5) решений, вида (27), для которой выполняется условие
![]() (29)
(29)
Равенство (29) определяет зависимость M = M(E), что позволяет сшить решения (см. пп. 3.1., 3.3.) и вычислить как собственные значения (энергии), так и собственные функции, удовлетворяющие условию нормировки (28).
Некоторые результаты расчётов представлены на рис. 2, 3. На рис. 2 представлена собственная функция, соответствующая наименьшему собственному значению (волновая функция основного состояния) в случае гнс = 0,4 (L= 0, Е= -0,5320). Зависимость величины наименьшего собственного значения (L = 0) от гнс представлена на рис. 3.
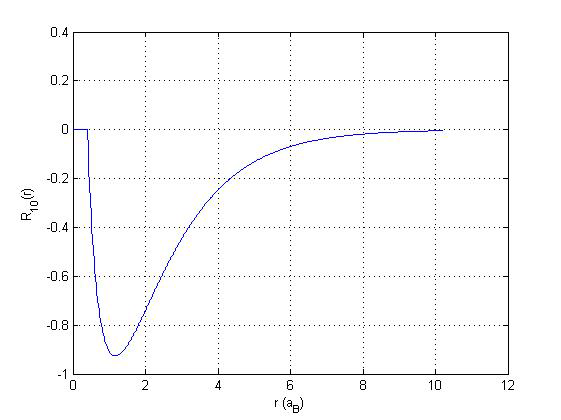
Рис. 2. Волновая функция основного состояния в случае радиуса потенциала rHC = 0,4 (l= 0, E= -0,5320)
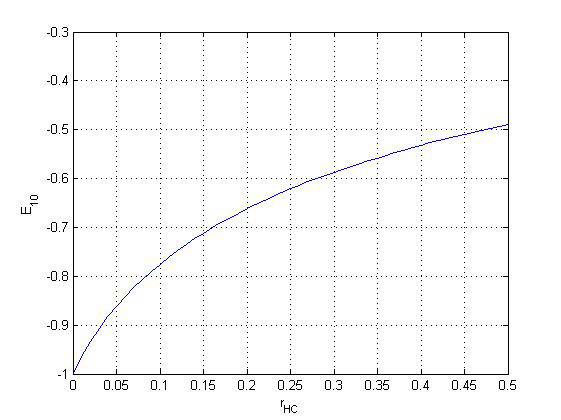
Рис. 3. Зависимость величины наименьшего собственного значения (l = 0) от гнс
Автор благодарен Т.Ю. Балыковой за проведение численных расчётов.
Литература
- Ландау Л.Д., Лифшиц Е.М. Квантовая механика. Нерелятивистская теория. − М.: Наука, 1989.
- Мессиа А. Квантовая механика. − М.: Наука, Т.1, 1978.
- Polupanov A.F., Kogan Sh.M. Lines intensities in shallow acceptor spectra in germanium. − Sov. Phys. Semicond. 1979, 13 (12), pp. 1368-1371.
- Pajot B., Beinikhes I.L., Kogan Sh.M., Novak M.G. Polupanov A.F., Song C. The interpretation of the p3/2 spectra of group III acceptors in silicon. − Semicond. Sci. Technol. 1992, 7, pp. 1162-1169.
- Polupanov A.F., Galiev V.I., Zhuravlev V.E. − Materials Science Forum. 1990, 65&66, pp. 4146.
- Galiev V.I., Polupanov A.F., Shparlinski I.E. On the construction of solutions of systems of linear ordinary differential equations in the neighbourhood of a regular singularity. − J. of Computational and Applied Mathematics, 1992, v. 39, pp. 151 -163.
- Galiev V.I., Polupanov A.F., Accurate solutions of coupled radial Schrödinger equations. − J. Phys. A: Math. Gen., 1999, v. 32, pp. 5477-5492.
- Федорюк М.В. Асимптотические методы линейных обыкновенных дифференциальных уравнений. − М.: Наука, 1985.
- Wasow W. Asymptotic expansions for ordinary differential equations. − New York, London, Sydney: Interscience Publishing, 1965.
- Polupanov A.F., Galiev V.I., Novak M.G. Effect of the spin-orbit interaction on the optical spectra of an acceptor in a semiconductor quantum dot. − Semiconductors, 1997, 31 (11), pp. 1185-1191.
- Yamasaki Sh. A new method for treating the hard core potential, − Progress of Theoretical Physics. 2006, 115 (1), pp. 89-114.
Информация об авторах
Метрики
Просмотров
Всего: 1146
В прошлом месяце: 1
В текущем месяце: 1
Скачиваний
Всего: 1139
В прошлом месяце: 4
В текущем месяце: 3