Моделирование и анализ данных
2014. Том 4. № 1. С. 109–120
ISSN: 2219-3758 / 2311-9454 (online)
Гипотеза Бейкера-Гаммеля-Уиллса о сходимости подпоследовательностей диагональных элементов таблицы аппроксимаций Паде
Аннотация
Общая информация
Ключевые слова: Гипотеза Бейкера-Гаммеля-Уиллса, сходимость подпоследовательностей, элементы таблицы аппроксимаций Паде
Рубрика издания: Математические исследования
Тип материала: научная статья
Для цитаты: Атращенко А.О. Гипотеза Бейкера-Гаммеля-Уиллса о сходимости подпоследовательностей диагональных элементов таблицы аппроксимаций Паде // Моделирование и анализ данных. 2014. Том 4. № 1. С. 109–120.
Полный текст
1. ОПРЕДЕЛЕНИЕ АППРОКСИМАЦИЙ ПАДЕ
Пусть
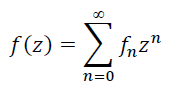 (1)
(1)
- степенной ряд (1), n и m - целые неотрицательные числа. По определению рациональная р-
функция ![]() —называется аппроксимацией Паде типа (n, m) степенного ряда 1, Qn,m
—называется аппроксимацией Паде типа (n, m) степенного ряда 1, Qn,m
если
![]() (2)
(2)
и имеет место равенство
![]() (3)
(3)
Обозначая j-й коэффициент Тейлора функции ![]() , непосредственно из определения получаем, что коэффициенты многочлена
, непосредственно из определения получаем, что коэффициенты многочлена ![]() являющегося знаменателем аппроксимации
являющегося знаменателем аппроксимации![]() , удовлетворяют следующей линейной
, удовлетворяют следующей линейной
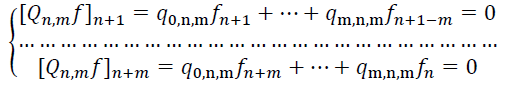 (4)
(4)


|
|
[1/0]f |
[2/0] f |
|
[n/0]f |
|
|
[0/1] f |
[1/1]r |
[2/1]r |
|
[^/1]f |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
l0/m|A |
[1/rn]f |
[2/rn]f |
|
[n/m]f |
|
|
|
|
|
|
|
|
Очевидно, что нулевая строка таблицы (когда фиксировано т = 0) - это обычная последовательность частичных сумм степенного ряда (1). В теории аппроксимаций Паде центральную роль играют вопросы сходимости элементов таблицы Паде - чаще всего строк, когда т фиксировано, п → ∞,, или диагонали таблицы Паде, когда п = m → ∞,. Проиллюстрируем преимущества аппроксимаций Паде, по сравнению с частичными суммами, на примере следующей простой функции
![]() (5)
(5)
голоморфной в круге |𝑧𝑧| < 1 и имеющей точку ветвления 𝑧𝑧 = −1, лежащую на границе этого круга. Вторая точка ветвления функции (5) – это точка 𝑧𝑧 = ∞. Хорошо известно, что последовательность частичных сумм функции (5) сходится к этой функции равномер-но на компактах, лежащих в круге |𝑧𝑧| < 1 (т.е. в круге до ближайшей особой точки), и расходится в любой точке вне замыкания этого круга. С другой стороны, известно, что диагональ ![]() таблицы аппроксимаций Паде функции (5) сходится к этой функции равномерно на компактах, лежащих в области
таблицы аппроксимаций Паде функции (5) сходится к этой функции равномерно на компактах, лежащих в области ![]() , т.е. во всей ком-плексной плоскости за исключением разреза [−∞,−1], соединяющего точки ветвления 𝑧 = ∞ и 𝑧 = −1 функции (5). Заметим также, что все нули знаменателей 𝑄𝑛,𝑛,n= 1,2,... , лежат на разрезе [−∞,−1], который является наиболее естественным разрезом среди всех разрезов, соединяющих точки ветвления 𝑧 = ∞ и 𝑧 = −1 функции (5). Кроме того,
, т.е. во всей ком-плексной плоскости за исключением разреза [−∞,−1], соединяющего точки ветвления 𝑧 = ∞ и 𝑧 = −1 функции (5). Заметим также, что все нули знаменателей 𝑄𝑛,𝑛,n= 1,2,... , лежат на разрезе [−∞,−1], который является наиболее естественным разрезом среди всех разрезов, соединяющих точки ветвления 𝑧 = ∞ и 𝑧 = −1 функции (5). Кроме того, ![]() ]– это максимальная область сходимости диагонали
]– это максимальная область сходимости диагонали ![]() . Это связано с тем, что если бы диагональ
. Это связано с тем, что если бы диагональ ![]() сходилась в большей области, то ее предельная функция давала бы голоморфное однозначное продолжение функции (5) в большую область, что невозможно, так как двузначная алгебраическая функция (5) не может быть однозначной ни в какой области, строго содержащей
сходилась в большей области, то ее предельная функция давала бы голоморфное однозначное продолжение функции (5) в большую область, что невозможно, так как двузначная алгебраическая функция (5) не может быть однозначной ни в какой области, строго содержащей ![]() .
.
2. ТЕОРЕМА МОНТЕССУ ДЕ БОЛОРА И ЕЕ ОБОБЩЕНИЕ
Наиболее ярким результатом о сходимости строк аппроксимаций Паде является следующая теорема Монтессу де Болора [2].

Частный случай m = 0 теоремы Монтессу де Болора совпадает с хорошо известным утверждением, что частичные суммы ряда Тейлора функции /, голоморфной в круге D, сходятся к f равномерно на компактах, лежащих в D.
Заметим, что предположение теоремы Монтессу де Болора о том, что функция f имеет в круге D = {|z| < R} ровно m полюсов (с учетом кратностей) является существенным. Без этого предположения теорема становится неверной (полюса аппроксимаций перестают “понимать, куда им следует притягиваться и в результате могут образовывать множество, всюду плотное во всей комплексной плоскости”). В общем случае (без этого предположения) можно утверждать только лишь, что ![]() Определение сходимости по емкости будет дано ниже (см. определение (27)). Кроме того, В.И. Буслаев, А.А. Гончар, и С.П. Суетин [3] в 1983 году показали, что равномерная сходимость имеет место по подпоследовательности в некотором меньшем круге. Точнее, они доказали следующую теорему.
Определение сходимости по емкости будет дано ниже (см. определение (27)). Кроме того, В.И. Буслаев, А.А. Гончар, и С.П. Суетин [3] в 1983 году показали, что равномерная сходимость имеет место по подпоследовательности в некотором меньшем круге. Точнее, они доказали следующую теорему.

Доказательство теоремы 1. Пусть ![]() . Непосредственно из определения аппроксимаций Паде имеем равенства
. Непосредственно из определения аппроксимаций Паде имеем равенства
![]() (6)
(6)
![]() (7)
(7)
Вычитая из равенства (6), умноженного на Qn+1(z), равенство (7), умноженное на Qn(z), получаем равенство
![]() (8)
(8)
Заметим, что степень многочлена, стоящего в левой части равенства (8), не превосходит (n + 1) + 2 = n + 3, а в правой части стоит ряд по степеням zn+3 и выше. Приравнивая коэффициенты при одинаковых степенях в левой и правой частях равенства (8) получаем равенство
![]() (9)
(9)
Разделив равенство (9) на (QnQn+1)(z), получим равенство
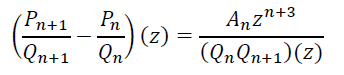 (10)
(10)
Воспользовавшись равенством (10), представим ![]() в следующем виде
в следующем виде
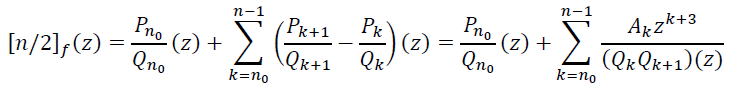 (11)
(11)
Из этого представления видно, что сходимость последовательности ![]() эквивалентна сходимости ряда
эквивалентна сходимости ряда
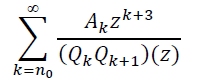 (12)
(12)
Напомним, что знаменатели 𝑄𝑛 имеют степень, не выше 2. Пусть 𝜁𝑛 и 𝜏𝑛 нули многочлена 𝑄𝑛.
Нормируем многочлены 𝑄𝑛 следующим образом:
![]()
А.А.Гончар доказал [4], что при такой нормировке радиус 𝑅𝑅(𝑓) голоморфности функции 𝑓 вычисляется по следующей формуле
![]() (13)
(13)
где 𝐴𝑛 - коэффициенты ряда (12). Кроме того, А.А.Гончар доказал [4], что ряд (12) равно-мерно сходится к 𝑓 на компактах, лежащих внутри множества {|𝑧|<𝑅(𝑓)}\𝐷𝜀 где множество 𝐷𝜀 можно покрыть объединением кругов, сумма радиусов которых не превосходит ε, где ε - произвольное наперед заданное положительное число. Таким образом,
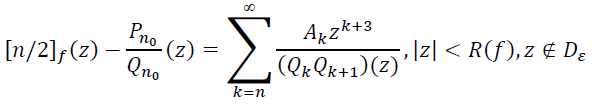 (14)
(14)
Так как по условию теоремы функция 𝑓 голоморфна в круге |𝑧|<1, то 𝑅(𝑓)≥1 и, следовательно, из формулы (13) имеем неравенство
![]()
Легко видеть, что это неравенство влечет за собой предельное равенство
![]()
где 𝛿 − произвольное сколь-угодно малое положительное число. Поэтому найдется под-последовательность 𝛬𝛿 натуральных чисел такая, что при всех 𝑛 ∈ 𝛬𝛿 и всех 𝑘 =0,1,… выполняются неравенства
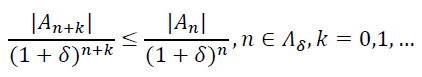 (15)
(15)
Фиксируем число r (0<𝑟<10−6) и предположим, что функция [𝑛/2]𝑓 при всех 𝑛 ∈ 𝜨 имеет полюс 𝜁𝑛𝑛 такой, что |𝜁𝑛|≤𝑟. Исходя из этого предположения, получим оценку снизу для 𝑟. Оценим правую часть равенства (14) при 𝑛 ∈ 𝛬𝛿. Так как при 𝑛 ∈ 𝛬𝛿 выполняются неравенства (15), то
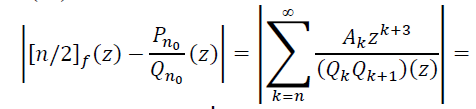 (16)
(16)
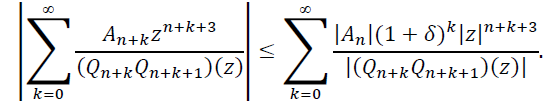
Следовательно,
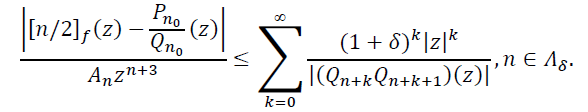 (17)
(17)
Фиксируем числа 𝑠,𝑡,𝑞 такие, что ![]() и положим
и положим
![]() (18)
(18)
Пусть 𝜏𝑛 − полюс [𝑛/2]𝑓 (ноль многочлена 𝑄𝑛), отличный от 𝜁𝑛. Обозначим через 𝐷𝑛,𝑘 круг радиуса ℎ𝑞𝑘 с центром в точке 𝜏𝜏𝑛+k, т.е
![]()
Обозначим через φ функцию, ставящую в соответствие каждому комплексному числу z его модуль \z\, т.е. φ(z) = \z\. Заметим, что функция φ переводит круг D𝑛,𝑘 в интервал
![]()
длина которого равна 2hqk. Следовательно, ![]() - это объединение интервалов, суммарная длина которых в силу определения (18) постоянной h не превосходит
- это объединение интервалов, суммарная длина которых в силу определения (18) постоянной h не превосходит
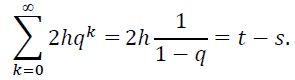
Поэтому на отрезке [5, t] длины t - s найдется точка р, не принадлежащая множеству ![]() . Это означает, что в множестве
. Это означает, что в множестве ![]() комплексной плоскости нет точек, по модулю равных р. Следовательно, окружность Гр = {IzI = р} лежит в кольце {𝑠≤|𝑧|≤t} и не пересекается с множеством
комплексной плоскости нет точек, по модулю равных р. Следовательно, окружность Гр = {IzI = р} лежит в кольце {𝑠≤|𝑧|≤t} и не пересекается с множеством ![]() . Поэтому при всех
. Поэтому при всех ![]() , ... имеем неравенства
, ... имеем неравенства
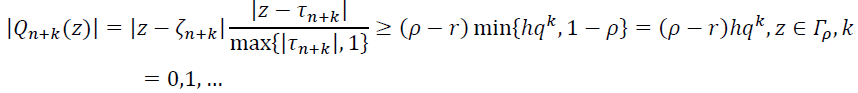
Оценивая при помощи этих неравенств правую часть неравенства (17), при ![]() получаем неравенство
получаем неравенство
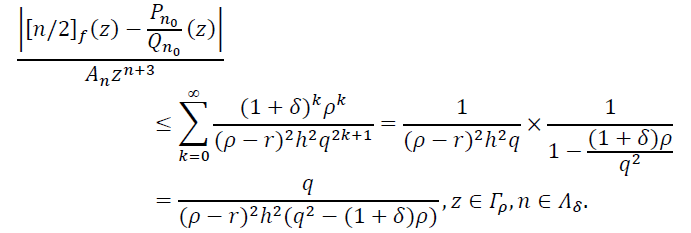
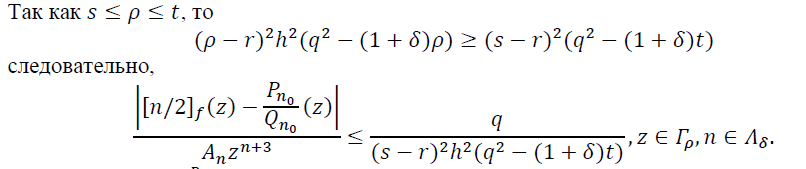
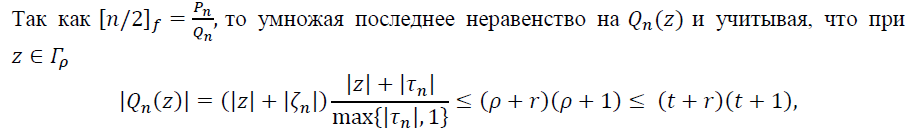
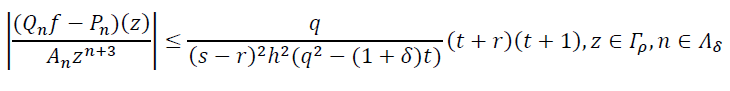 (19)
(19)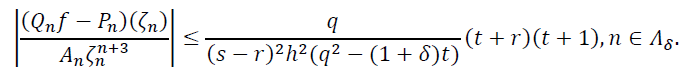
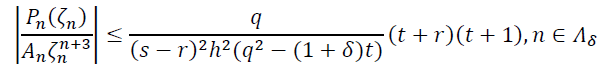 (20)
(20)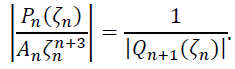
Отсюда и (20) имеем неравенство
![]()
или, что, то же самое, неравенство
![]() (21)
(21)
Так как
![]()
то из неравенства (21) получаем неравенство
![]()
Так как полученное неравенство не зависит от п, а число 𝛿 сколь-угодно мало, то тем самым имеем неравенство
![]()
Отсюда и определения (18) постоянной h получаем неравенство
![]() (22)
(22)
Так как оцениваемая величина r окажется достаточно малой, то имеет смысл выбрать параметры 𝑡 и 𝑞 так, чтобы максимизировать величину
![]()
Приравнивая к нулю частные производные по 𝑡 и 𝑞 функции 𝛷(0,𝑡,𝑞) получаем следую-щую систему
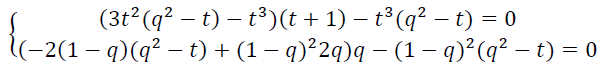
эквивалентную системе
![]()
В качестве приближенного решения последней системы можно взять следующие параметры: ![]() При таких параметрах неравенство (23) приобретает следующий вид:
При таких параметрах неравенство (23) приобретает следующий вид:
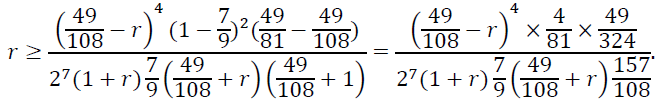 (23)
(23)
Легко видеть, что из неравенства (24) следует, что г ≥ 10-6. Таким образом, теорема доказана.
3. ТЕОРЕМА ШТАЛЯ И КОНТРПРИМЕР К ГИПОТЕЗЕ ШТАЛЯ
Одним из наиболее глубоких результатов о сходимости диагонали таблицы аппроксимаций Паде является теорема Шталя [5], [6] о сходимости диагонали таблицы аппроксимаций Паде многозначных алгебраических функций. Напомним, что функция f (z) называется алгебраической функцией, если она является решением уравнения
![]()
где Ро (z),..., Рк (z) — некоторые многочлены. Теорема Шталя может быть сформулирована как для вышеопределенных аппроксимаций Паде с центром в точке z = 0, так и для аппроксимаций Паде с центром в точке z = ∞. В последнем случае теорема Шталя становится более наглядной.
Напомним определение аппроксимаций Паде с центром в точке z = ∞.
Пусть
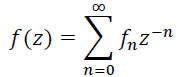 (25)
(25)

![]()
Перед формулировкой теоремы Шталя напомним также определение трансфинитного диаметра компакта 𝐾, лежащего в комплексной плоскости:
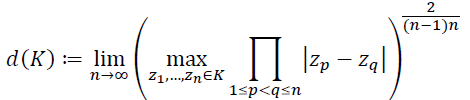 (26)
(26)



![]() (27)
(27)
Таким образом, для произвольных алгебраических функций равномерная сходимость может отсутствовать. Однако, рассмотренный в §1 пример простой функции f(z) = ![]() наводит на мысль, что если на алгебраическую функцию наложить некоторые дополнительные ограничения, то по некоторой подпоследовательности такая равномерная сходимость может и возникнуть. В частности, 1996 году Г. Шталь высказал следующее предположение о сходимости диагонали таблицы аппроксимаций Паде с центром в точке z=0 гиперэллиптических функций [7].
наводит на мысль, что если на алгебраическую функцию наложить некоторые дополнительные ограничения, то по некоторой подпоследовательности такая равномерная сходимость может и возникнуть. В частности, 1996 году Г. Шталь высказал следующее предположение о сходимости диагонали таблицы аппроксимаций Паде с центром в точке z=0 гиперэллиптических функций [7].
![]()
Гипотеза Шталя является уточнением старой высказанной в 1961 году гипотезы Бейкера-Гаммеля-Уиллса, в которой функция f - это произвольная голоморфная в круге функция, т.е. в гипотезе Бейкера-Гаммеля-Уиллса в отличие от гипотезы Шталя нет условия гиперэллиптичости функции. Таким образом, если гипотеза Шталя неверна, то гипотеза Бейкера-Гаммеля-Уиллса тем более будет неверна.
Сам же Г. Шталь и доказал в [7] свою гипотезу в ситуации общего положения, т.е. при некоторых весьма общих предположениях на нули и полюсы рациональных функций г1и г2.
Тем не менее, оказалось, что в общем случае (в отсутствие дополнительных условий на нули и полюсы рациональных функций г1и г2) гипотеза Шталя неверна. Соответствующий пример, указанный В.И.Буслаевым [8], дается гиперэллиптической функцией
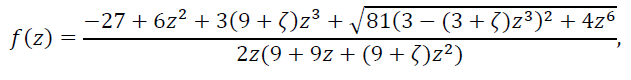 (28)
(28)

Итак, гиперэллиптическая функция (28) опровергает гипотезу Шталя. Однако, по аналогии с теоремой Буслаева-Гончара-Суетина имеет смысл говорить о модифицированной гипотезе Шталя.

Легко видеть, что модифицированная гипотеза Шталя верна тогда и только тогда, когда с>0. C другой стороны, так как основной вариант гипотезы Шталя неверен, то с<1. Более того, как показывает пример Буслаева
с≤ 0,9841. (29)
В данной дипломной работе решается следующая задача.
Задача. Найти верхнюю оценку постоянной с, фигурирующей в модифицированной гипотезе Шталя, улучшающую оценку (29).
Ответ на поставленную задачу содержится в следующей теореме.
Теорема 2. Для постоянной с, фигурирующей в модифицированной гипотезе Шталя, имеет место верхняя оценка
с ≤ 0,9638. (30)
Очевидно, что верхняя оценка (30) точнее оценки (29).

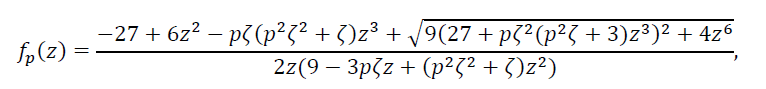 (31)
(31)

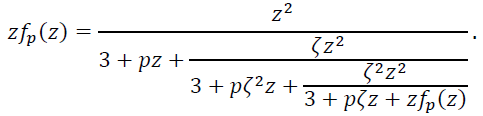
Следовательно, функция 𝑓𝑝 (𝑧) имеет следующее разложение в периодическую (с периодом 3) непрерывную дробь
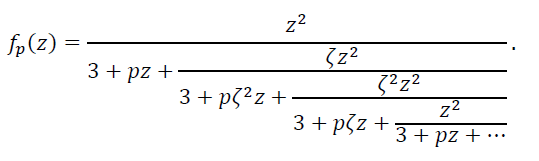 (32)
(32)
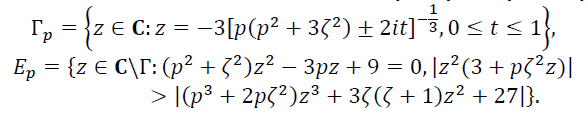

Из полученных данных образуем таблицу:
|
p |
mp/Mp |
|
0,4 + 2,598i |
0,9768 |
|
0,23131 + 2,598i |
0,981 |
|
1,5 + 2,598i |
0,9841 |
|
1,5 + 2i |
0,9875 |
|
1,5 + 6,235i |
0,9945 |
|
0,8 + 2,598i |
0,9788 |
|
0,56321 + 2,598i |
0,9774 |
|
0,3333 + 2,598i |
0,9767 |
|
0,569 + 0,2568i |
2,658 |
|
0,569 + 0,2568i |
2,658 |
|
2356 + 0,2365i |
1 |
|
5,004 + 0,2365i |
1,006 |
|
0,3111 + 3,345i |
0,9851 |
|
0,3111 + 2,345i |
0,9757 |
|
0,3111 + 2,222i |
0,9752 |
|
0,3111 + 2,1112i |
0,9752 |
|
0,6111 + 2,1112i |
0,9712 |
|
0,5111 + 2,1112i |
0,9695 |
|
0,4111 + 2,1112i |
0,9679 |
|
0,211 + 2,1112i |
0,9824 |
|
0,461 + 2,1112i |
0,9687 |
|
0,413 +2,11i |
0,968 |
|
0,411 + 2,13i |
0,9684 |
|
1,411 + 1,119i |
1,045 |
|
1,411 + 0,119i |
1,527 |
|
1,411 + 12,119i |
0,9986 |
|
1,411 - 9,119i |
0,9995 |
|
0,4432 +2,111i |
0,9684 |
|
0,32 +2,111i |
0,9745 |
|
0,352 +2,111i |
0,9722 |
|
0,552 +2,111i |
0,9702 |
|
3 |
1,032 |
|
0,455 +1,9i |
0,9638 |

![]()

Благодарность
Выражаю глубокую благодарность моему научному руководителю доктору физикоматематических наук профессору Виктору Ивановичу Буслаеву.
Литература
- Бейкер Дж., Грейвс-Моррис П. Аппроксимации Паде. − М.: Мир, 1986.
- de Montessus de Ballore R. Sur les fractions continues algebriques . − Bull. Soc. Math. France, 1902, v. 30, pp. 28-36.
- Буслаев В.И., Гончар А.А., Суетин С.П., О сходимости подпоследовательностей m-й строки таблицы Паде . − Матем. сб., 1983, т.120, №4, с.540-545.
- Гончар А.А., Полюсы строк таблицы Паде и мероморфное продолжение функций. − Матем. сб., 1981, т. 115 (157), 4, c. 590-613.
- Stahl H. Orthogonal polynomials with complex valued weight function. I,II . − Constr. Ap-prox., 1986, vol. 2, pp. 225-240, 241-251.
- Stahl H. Extremal domains associated with an analytic function. I,II . − Complex Variables Theory Appl., 1985, vol. 4, pp. 325-338, 339-354.
- Stahl H. Diagonal Pade Approximants to Hyperelliptic functions. − Ann. Fac. Sci. Toulouse Math. (6), Spec. Iss. 1996, pp. 121-193.
- Буслаев В.И. О гипотезе Бейкера-Гаммеля-Уиллса в теории аппроксимаций Паде . − Матем. сб., т. 193, №6, 2002, с.25-38.
Информация об авторах
Метрики
Просмотров
Всего: 1129
В прошлом месяце: 4
В текущем месяце: 1
Скачиваний
Всего: 505
В прошлом месяце: 0
В текущем месяце: 1