О задаче формирования портфеля облигаций по вероятностному критерию в модели Кокса-Ингерсолла-Росса

Рассматривается задача формирования портфеля купонных облигаций в случае, когда динамика процентных ставок описывается моделью Кокса-Ингерсолла-Росса. В качестве критерия оптимальности выбрана функция вероятности, что приводит к задаче стохастического программирования с вероятностным критерием. Решение задачи стохастического программирования получено с использованием гладкой аппроксимации функции вероятности и ее производных и метода проекции градиента. Приводится пример расчета оптимальной структуры портфеля.

Введение
 

Облигации являются основой инвестиционного портфеля ключевых институциональных инвесторов, таких как страховые компании и негосударственные пенсионные фонды. Облигация — это долговая ценная бумага, гарантирующая держателю получение фиксированной суммы, называемой номиналом, в момент погашения облигации, а также промежуточных процентных выплат, называемых купонами, если они предусмотрены для конкретной облигации. Облигации позволяют компании их выпустившей — эмитенту — получить финансирование в большем объеме и на более привлекательных условиях, в сравнении с банковскими кредитами, если на облигации этого эмитента будет спрос. В свою очередь, для инвестора — покупателя облигаций —  это способ вложить средства зачастую под более высокую ставку, чем на банковском вкладе, и при этом иметь возможность практически в любой момент времени продать облигацию и получить свои деньги без потери процентного дохода. 

Для бескупонных облигаций и облигаций с фиксированным купоном все будущие выплаты заранее известны владельцу облигации, если пренебречь риском неисполнения обязательств со стороны эмитента. Риск полного или частичного неисполнения обязательств также называется кредитным риском. При этом, даже в отсутствие кредитного риска, облигации нельзя рассматривать как полностью безрисковый инструмент. Причина кроется в колебаниях рыночных цен облигаций во времени вплоть до момента их погашения. Инвестор не может заранее определить цену, по которой он сможет продать или купить облигации в произвольную дату до момента их погашения. Основным фактором, влияющим на рыночные цены уже существующих облигаций является рыночная ставка заимствований, отражающая доходность вложений денежных средств в текущий момент времени. Эта же ставка определяет доходность новых выпусков облигаций на рынке. Рост рыночной ставки означает появление новых выпусков облигаций с более высокой доходностью и, как следствие, к снижению цен уже обращающихся на рынке бумаг. Снижение цен облигаций в свою очередь приводит к росту их доходности (для новых владельцев), что в итоге компенсирует изменение ставок. Напротив, снижение рыночных ставок ведет к росту цен старых выпусков облигаций и снижению их доходности, так как купонные ставки по ним будут предпочтительнее в сравнении с новыми выпусками. Формирование портфеля из облигаций с разным сроком до погашения и разными купонными ставками может помочь инвестору снизить риски существенного снижения цены портфеля при колебаниях ставки. 

Задачам формирования оптимального портфеля ценных бумаг посвящено огромное количество книг и статей. Основополагающие результаты были получены Гарри Марковицем в 1952 году [1]. Он математически сформулировал задачу формирования портфеля ценных бумаг с учетом ожидаемой доходности и риска. Доходность портфеля рассматривалась как случайная величина, зависящая от случайных же доходностей отдельных активов, входящих в портфель. Мерой риска являлась дисперсия доходности итогового портфеля.  

Постановка задачи и результаты Марковица открыли множество вопросов для дальнейшего исследования. Каким образом моделировать доходности активов в портфеле? Каким образом учитывать возможности ребалансировки портфеля, то есть изменения его структуры во времени? Какой критерий оптимальности портфеля или меру риска выбрать? Мера риска в форме дисперсии доходности имеет очевидный недостаток — если отклонения доходности от средней в меньшую сторону нежелательны для инвестора, то отклонения в большую сторону для инвестора выгодны. Минимизация же дисперсии ограничивает отклонения в обе стороны. С течением времени одним из наиболее популярных критериев стал VaR-критерий (value-at-risk), также называемый квантильным критерием [2,3]. Квантильный критерий в задачах формирования оптимального портфеля ценных бумаг отражает либо минимальный уровень дохода, который будет получен с заданной вероятностью, или же максимальный уровень потерь, который будущие потери не превзойдут с той же заданной вероятностью. Схожим по смыслу и подходам к исследованию является вероятностный критерий, который отражает вероятность того, что доходность окажется не меньше заданного уровня, или же что потери не превысят заданный порог. Подробно свойства и взаимосвязь квантильного и вероятностного критериев описаны в [5]. 
 Для моделирования доходностей финансовых активов также разработаны различные подходы. В [4] для моделирования доходностей двух рисковых активов используется равномерное распределение, являющееся наихудшим для вероятностного критерия [5]. В [6] для моделирования цен акций использовался аппарат копул, при этом задача формирования оптимального портфеля не исследовалась. В [7] исследуется оценка VaR-критерия для негауссовского распределения доходностей активов.  

Важно отметить, что наибольшее число исследований посвящено задачам формирования оптимального портфеля акций или производных финансовых инструментов, когда основная часть средств направляется на приобретение рисковых активов  без гарантий дохода и возврата средств, но с более высокой ожидаемой доходностью. При этом предполагается возможность вложения части средств в безрисковый актив. Ставка доходности безрискового актива в целях упрощения, как правило, полагается известной и постоянной. Это допущение становится неадекватным в случае, когда портфель преимущественно или полностью состоит из облигаций. В этом случае необходимо учитывать рисковую природу вложений в облигации, то есть зависимость цен от динамики процентных ставок. Одной из основных моделей процентных ставок является модель Васичека [7], а ее развитием — модель Кокса-Ингерсолла-Росса [8]. 

В [9] представлено решение задачи формирования оптимального портфеля бескупонных облигаций по вероятностному критерию. Однако, рассмотренная в [9] модель имеет ряд существенных ограничений. Во-первых, в портфель облигаций не включались купонные облигации, хотя именно такие бумаги наиболее распространены на рынке. Во-вторых, изменения цен облигаций во времени упрощенно моделировались с помощью многомерного гауссовского вектора.  В-третьих, для решения задачи исходный функционал доходности заменялся на его линейную аппроксимацию. Таким образом, влияние изменений рыночной ставки заимствований учитывалось лишь косвенно (через допущение о возможной зависимости компонент гауссовского вектора), а модель динамики рыночной ставки не учитывалась вовсе. 

В данной статье рассматривается модель портфеля купонных облигаций, упорядоченных по сроку до погашения, в которой все промежуточные выплаты — суммы купонов и номинала при погашении — инвестируются в бумагу с максимальным сроком до погашения, аналогично [9]. Для моделирования процентной ставки и изменений цен облигаций используется модель Кокса-Ингерсолла-Росса. Поскольку цены покупки самой «длинной» облигации в даты промежуточных выплат заранее неизвестны, такой портфель также подвержен рыночному риску. Итоговое количество наиболее длинных облигаций в портфеле на момент погашения заранее неизвестно. Для минимизации негативного влияния рыночного риска рассматривается задача формирования оптимального портфеля облигаций по вероятностному критерию — то есть задача формирования такого портфеля, для которого вероятность превышения заданного уровня итоговым капиталом будет максимальна. 

В первой части статьи приводятся основные допущения модели, описывается процесс динамики  процентной ставки и формула расчета рыночной цены облигации с заданными параметрами. Во второй части статьи описывается модель портфеля облигаций  и формулируется задача стохастического программирования с вероятностным критерием. В третьей части описывается подход к решению задачи стохастического программирования, основанный на гладкой аппроксимации функции вероятности и ее градиента. В четвертой части приводится пример расчетов. 

Теоретическая часть

Перечислим основные допущения, используемые в модели портфеля облигаций: 

1. все ценные бумаги бесконечно делимы, то есть существует возможность купить или продать нецелое количество облигаций;
2. отсутствуют комиссии за сделки и задержки в исполнении сделок;
3. единичная сделка не оказывает влияния на рыночные цены независимо от объема;
4. отсутствуют кредитный и инфраструктурный риски;
5. все выплаты реинвестируются в облигацию с максимальным сроком до погашения;
6. портфель удерживается до погашения всех облигаций;
7. выплаты купонов и номинала облигаций происходят в дискретные моменты времени с заданным шагом;
8. «короткие» продажи запрещены;
9. динамика процентных ставок описывается процессом Кокса-Ингерсолла-Росса (CIR процесс).
    

Допущения 1-3 обеспечивают возможность проведения сделок любого объема на рыночных условиях. Допущение 7 позволяет снизить размерность задачи, а также пренебречь расчетом накопленного купонного дохода по облигации при ее покупке.  
        Модель CIR динамики процентной ставки задается стохастическим дифференциальным уравнением [8]:

 dr = a  ( μ − r   )  dt + r   σdW t    ,(1) 
где  μ   – равновесная (средняя) ставка,    r 0    и   r   – начальная и текущая ставки заимствований,       a   – скорость возвращения к средней ставке,   σ   – коэффициент волатильности,   W t    - винеровский процесс. 

Модель Кокса-Ингерсолла-Росса является примером однофакторной модели, поскольку учитывает лишь один источник неопределенности будущих ставок через винеровский процесс. Как и модель Васичека, обладает свойством возвращения к среднему. Это важное свойство, поскольку оно не допускает ни бесконечного роста процентных ставок, ни снижения ставок ниже уровня, при которым инвестиции становятся невозможными. Отрицательные ставки в рамках модели Кокса-Ингерсолла-Росса невозможны. 
        Модель CIR позволяет аналитически найти цену бескупонной облигации как функцию от текущей процентной ставки, оставшегося срока до погашения облигации и параметров процесса. Для заданной текущей процентной ставки   r ( t  )     цена бескупонной облигации со сроком до погашения   T   вычисляется по формулам: 
 P ( t , T   )  = A  ( t , T   )  e − B  ( t , T   )  r ( t  )      ,(2) 
 A ( t , T   )  = ( 2 he ( a + h   )  ( T − t   )  / 2     2 h + ( a + h   )   ( e h ( T − t   )    − 1   )     )  2 aμ  σ 2       ,(3) 
 B ( t , T   )  = 2 ( e h ( T − t   )    − 1   )   2 h + ( a + h   )   ( e h ( T − t   )    − 1   )       (4) 
 h = a 2  + 2  σ 2      .(5)
Стоимость купонной облигации может быть определена как стоимость портфеля бескупонных облигаций с идентичным денежным потоком, когда бескупонная облигация с заданным сроком погашения «подменяет» в расчете купонную выплату в ту же дату: 
 P ( t , T   )  + ∑ i = [ t  ]  + 1   T  c   P ( t , i   )    .(6)

 
Математическая модель портфеля облигаций

Для модели портфеля облигаций примем следующие обозначения: 
 N   – количество видов облигаций, упорядоченных по сроку погашения;
 
 T N    – горизонт инвестирования (в купонных периодах);
 
 u i    – количество облигаций i-го вида в момент формирования портфеля;
 
 T i    – срок до погашения i-й облигации;
 
 c i    – ставка купона i-й облигации;
 
 K   – первоначальный капитал.

Без ограничения общности положим номинал всех облигаций равным 1.
Цена последней облигации в момент времени t определяется как приведенная стоимость будуших выплат по этой облигации (купонных платежей и номинала) в соответствии с формулой (6): 
 S N  ( t  )  = P  ( t , T N    )  + ∑ i = [ t  ]  + 1   T N   c N    P ( t , i   )    .(7)
Общая сумма поступлений от облигаций i-го вида определяется выражением: 
 ∑ u i   с i  ⋅ I [ j ≤ T i    ]  + u i   ⋅ I [ j = T i    ]    .(8)
Задав все параметры можно рассчитать итоговый капитал инвестора для заданной начальной структуры портфеля:

 C ( u , S   )  = ∑ i = 1  N  ( u i  S N  ( T i   )    + ∑ k = 1  T i   u i  r i   S N  ( k  )       )   = ∑ i = 1  N  u i  S N  ( T i   )    + ∑ i = 1  N  ∑ k = 1  T i   u i  r i   S N  ( k  )           (9)
  
Случайный вектор    S = ( S N  ( 1  )  , S N  ( 2  )  , … , S N  ( T N   )    )     состоит из цен N-й облигации в заданные моменты времени. Первая часть суммы соответствует сумме выплаты номинала по последней облигации, приобретенной как в начальный момент времени так и на средства от погашения остальных облигаций в портфеле в заданные моменты времени, без учета купонных платежей. Второе слагаемое соответствует количеству N-х облигаций, приобретенных на поступившие купонные платежи.

 Сформулируем оптимизационную задачу. В качестве критерия будем использовать функцию вероятности [5]. В данной задаче функцию вероятности определим как функционал, зависящий от вектора u, значение которого равно вероятности того, что итоговый капитал превысит заданный уровень:  
 P ϕ  ( u  )  = P  { C ( u , S   )  ⩾ ϕ   }  = M  [ I [ C ( u , S   )  ⩾ ϕ   ]    ]    .(10)
Получаем задачу максимизации функции вероятности

 P φ  ( u  )  → max u    ,(11)
с ограничениями 
 ∑ i = 1  N  u i   S i  ( 0  )  ⩽ K   ,(12) 
 u i  ⩾ 0 , i = 1  , … , N   .(13)
 
 Задача (11) с ограничениями (12) и (13) является задачей стохастического программирования с вероятностным критерием. Область допустимых стратегий представляет собой многомерный тетраэдр с вершиной в начале координат и ребрами, лежащими на осях координат, а в случае двух видов облигаций в портфеле — треугольник.

Решение задачи стохастического программирования 

Для решения задачи стохастического программирования будем использовать метод проекции градиента. Для оценки градиента будем использовать гладкую аппроксимацию [10] функции вероятности и ее производных. Основная идея аппроксимации – замена разрывной функции Хевисайда в интегральном представлении функции вероятности на сигмоидальную функцию (сигмоиду). Сигмоида является функцией распределения случайной величины, распределенной по логистическому закону с нулевым средним и конечной дисперсией: 

 S θ  ( y  )  = 1 1 + e − θy      ,   (14)
  
где параметр  θ ≫ 0    определяет крутизну кривой в окрестности нуля и точность аппроксимации. 

 Аппроксимация функции вероятности принимает вид:  
 P φ θ  ( u  )  = ∫ G ❑  S θ  ( C ( u , S   )  − φ    )  f ( x  )  dx   = M  [ S θ  ( C ( u , S   )  − φ    )    ]    , (15) 
где    G   — носитель распределения случайного вектора S.

 Введем обозначение для производной сигмоиды:  
 S '  θ  ( x  )  = θ  S θ  ( x  )  ( 1 − S θ   ( x  )    )    .(16)
  
Аппроксимация частных производных по компонентам вектора управления   u i    при   i = 1 , m  ¯      и частной производной по уровню потерь принимают вид:

∂ P φ θ  ( u  )   ∂ u i    = M  [ S '  θ  ( C ( u , S   )  − φ    )  C '  u i   ( u , S   )    ]    , (17) 
 ∂ P φ θ  ( u  )   ∂ φ   = − M   [ S '  θ  ( C ( u , S   )  − φ    )    ]    . (18)
  
В [10-11] доказана поточечная сходимость аппроксимаций функции вероятности и ее производных для любого  i = 1 , m  ¯       при  θ → ∞   :  P φ θ  ( u  )  → P φ  ( u  )  , ∂ P φ θ  ( u  )   ∂ φ   → ∂ P φ  ( u  )   ∂ φ   , ∂ P φ θ  ( u  )   ∂ u i    → ∂ P φ  ( u  )   ∂ u i      . (19)
 
 В исследуемой задаче нельзя в явном виде записать плотность распределения вектора цен облигаций в моменты ее покупки. Более того, размерность вектора цен будет расти при увеличении количества купонных периодов и количества различных облигаций, включаемых в портфель. Высокая размерность вектора случайного вектора затрудняет получение точных оценок функции вероятности и ее производных численными методами интегрирования. 
 Для вычисления приближенных значений функции вероятности и ее производных будем использовать метод Монте-Карло. Для этого необходимо сгенерировать пучок траекторий процесса CIR. Далее для каждой траектории определить значения процентной ставки в моменты получения купонных выплат и погашения облигаций в портфеле. По выборке значений процентной ставки в заданные моменты времени рассчитать стоимость  последней облигации для заданной ставки в эти моменты времени Таким образом, из пучка траекторий получается выборка реализаций случайного вектора S. Значения функции вероятности и ее производных вычисляются как математические ожидания соответствующих функций на полученной выборке.  

 Реализация и пример

Для решения исследуемой задачи разработана программа на языке Python, использующая модули программного комплекса [12]. Входными данными для работы программы являются параметры процесса CIR, сроки облигаций и их купонные ставки. Знание сроков облигаций и купонных ставок позволяет рассчитать денежные потоки от каждой облигации и от портфеля в целом в каждый момент времени. По этим данным можно сформировать функцию итогового капитала по формуле (9), зависящую от случайных цен последней облигации, и функцию ограничений по формуле (12). Построение функций по исходным данным, расчет функции вероятности и ограничений, а также расчет их производных осуществляется автоматически. Отметим, что функция (9) является линейной по компонентам вектора u. 
 Для наглядности и простоты интерпретации результатов рассмотрим пример портфеля облигаций двух видов со сроками до погашения 2 и 5, которые приобретаются при размещении на первичном рынке по цене номинала, то есть по цене 1. Ставку купона по второй облигации положим равной 5% и проанализируем зависимость структуры оптимального портфеля от ставки купона по первой облигации. Зададим следующие параметры CIR-процесса:  
 μ = 5  % , σ = 0.5  , a = 2  , r 0  = 15  % .   

 При заданных параметрах ставка с начального значения 15% будет снижаться и стремиться к равновесному значению 5%, что будет приводить к росту цены второй облигации, ее покупка на промежуточные выплаты будет обходиться дороже, чем в начальный момент времени. Первоначальный капитал положим равным 10, а желаемый уровень итогового капитала определим как  
 φ = 10  ( 1 + 0.06   )  5.    ,

то есть доходность вложений на 5 периодов (например, лет) должна на 1 процентный пункт превышать равновесную ставку 5%.
 Для расчета функции вероятности и ее производных по заданным параметрам сгенерировано 20 000 траекторий CIR-процесса и сформирована выборка реализаций случайного вектора S. Значение параметра  θ   примем равным 5. На рис. 1 представлена зависимость оптимального количества облигаций первого типа в момент формирования портфеля и значения вероятностного критерия. Видно, что с ростом ставки купона по первой облигации вероятность получения капитала не ниже заданного сперва остается неизменной, поскольку эта облигация не включается в портфель, а затем растет. Оптимальная структура портфеля в зависимости от ставки купона предполагает либо вложение всех средств во вторую облигацию, либо только в первую с последующей покупкой второй.  
    
       

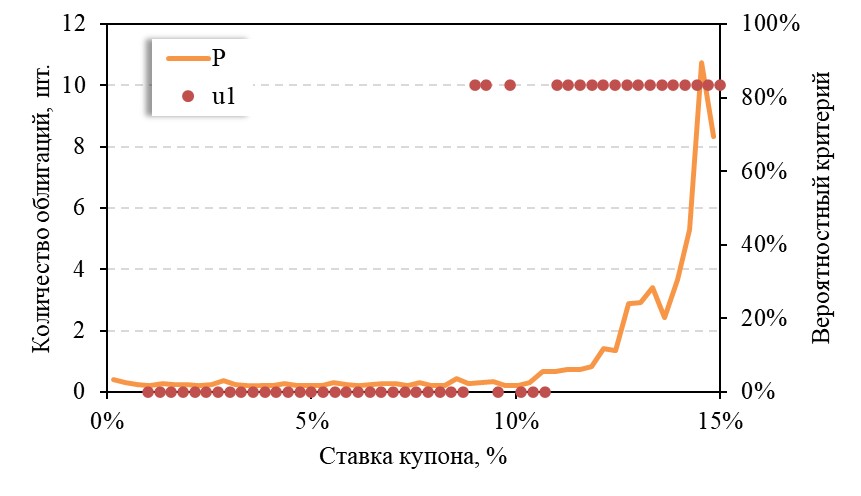
Рис. 1. График зависимости структуры портфеля от ставки купона.
 
        Из приведенного примера следует особенность вероятностного критерия в задаче формирования оптимального портфеля ценных бумаг — оптимальная структура портфеля может не предполагать диверсификации вложений в разные ценные бумаги. Более того, если два портфеля с разной ожидаемой доходностью обеспечивают равную (или очень близкую) вероятность достижения требуемой доходности, то по вероятностному критерию более доходный вариант не окажется предпочтительным. Таким образом, на основе полученных результатов следует продолжить исследование различных постановок задач. Например, можно перейти к задаче максимизации ожидаемой доходности при ограничении на вероятность достижения минимальной требуемой доходности. Для этого могут быть использованы уже разработанные программные модули. Другой вариант может быть связан с использованием функции интегральной квантили (CVaR) в качестве критерия, для которого аналогичные инструменты пока не разработаны. Отметим также, что в случае когда облигации в начальный момент времени приобретаются по рыночной цене, а не номинальной стоимости как при первичной продаже эмитентом, ожидаемые изменения ставки и цены облигации уже будут заложены в ее начальную стоимость, то есть ожидаемая доходность вложений в каждую облигацию при отсутствии кредитного риска будет одинаковой. В этом случае влияние структуры портфеля на значение вероятностного критерия будет слабым и трудно интерпретируемым. 

Заключение
       

В статье исследована модель портфеля облигаций, в котором все промежуточные поступления от купонных выплат и погашения облигаций направляются на покупку облигации с максимальным сроком до погашения. Динамика процентных ставок и цен облигаций моделируется с помощью процесса Кокса-Ингерсолла-Росса. Для такой модели составлена задача стохастического программирования с вероятностным критерием и предложен подход к ее решению. То есть впервые получено решение задачи формирования  портфеля купонных облигаций по вероятностному критерию с учетом особенностей динамики процентных ставок и ценообразования облигаций. Численный пример показывает адекватные изменения в структуре портфеля при изменении ставок купона. Также из примера следует, что использование вероятностного критерия может приводить к отсутствию диверсификации вложений, что на практике представляется нежелательным. Предполагается дальнейшее исследование модели в части учета кредитного риска по облигациям и в части влияния критерия оптимальности на итоговую структуру портфеля.

1. Markowits Harry M. Portfolio Selection // Journal of Finance. 1952. 7. № 1 pp. 71-91.
2. Кибзун А.И., Кузнецов Е.А. Оптимальное управление портфелем ценных бумаг // Автоматика и телемеханика. 2001. № 9. С.101–113.
3. Григорьев П.В., Кан Ю.С. Оптимальное управление по квантильному критерию портфелем ценных бумаг // Автоматика и телемеханика. 2004. № 2. С. 179–197.
4. Игнатов А.Н., Кибзун А.И. Двухшаговая задача формирования портфеля ценных бумаг из двух рисковых активов по вероятностному критерию // Автоматика и телемеханика. 2015. №7. С. 78–100.
5. Кан Ю.С., Кибзун А.И. Задачи стохастического программирования с вероятностными критериями. М.: Физматлит, 2009.
6. Барышева А.Е., Марков А.С., Мицель А.А. Оценка VaR при негауссовом распределении доходностей активов // Российский технологический журнал. 2020. №8(2). С.67-84.
7. Vasicek O. An equilibrium characterization of the term structure // J. Financial Economics. 1977. V. 5. P. 177-188.
8. Cox J., Ingersoll J., Ross S. A Theory of the term structure of interest rate // Econometrica. 1985. V. 53. P. 385-407.
9. Кан Ю.С., Сысуев А.В. О приближенном решении задачи формирования портфеля ценных бумаг с фиксированным доходом // Автоматика и телемеханика. 2010. № 6. С. 130–141.
10. Соболь В.Р., Торишный Р.О. О гладкой аппроксимации вероятностных критериев в задачах стохастического программирования // Тр. СПИИРАН. Т. 19. № 1. 2020. С. 180—217
11. Sobol V., Torishnyi R. Smooth approximation of probability and quantile functions: vector generalization and its applications // Journal of Physics: Conference Series. 1925 012034. 2021. P. 1–10.
12. Торишный Р.О. Программный комплекс для анализа задач стохастического программирования с вероятностным критерием // ВКиТ. 2022. Т. 19. No 5(215). С. 3–12.