Психологическая наука и образование
2003. Том 8. № 4
ISSN: 1814-2052 / 2311-7273 (online)
Учет индивидуальных особенностей мышления при обучении учащихся решению математических задач
Аннотация
Общая информация
Ключевые слова: математическое мышление, решение задач, Пиаже Ж.
Рубрика издания: Психология образования
Для цитаты: Каплунович И.Я., Верзилова Н.И. Учет индивидуальных особенностей мышления при обучении учащихся решению математических задач // Психологическая наука и образование. 2003. Том 8. № 4.
Полный текст
Одним из важнейших показателей эффективности работы и профессионализма педагога является учет индивидуальных особенностей учащихся в процессе обучения (в частности, математике). Различий, по которым должно и можно дифференцировать школьников, достаточно много. Проранжировать их очень трудно (да и невозможно). Тем не менее вряд ли у кого вызовет сомнения тот факт, что одной из важнейших характеристик, на которую должен опираться и которую обязан учитывать преподаватель «гимнастики ума», являются особенности математического мышления учащихся.
Каждый уважающий себя педагог пытается это делать. Однако очень часто его деятельность носит чисто интуитивный, хаотический, характер. Одна из основных причин этого кроется в том, что сеятель «разумного, вечного, доброго» незнаком со структурой математического мышления. Трудно не согласиться с Конфуцием, задавшим более двух с половиной тысяч лет назад совсем не риторический вопрос: «Если ты не знаешь, что ты ищешь, то что ты ищешь?» Действительно, вряд ли можно формировать то, чего не знаешь, развивать феномен, со структурой которого незнаком. Поэтому, занимаясь проблемой развития математического мышления учащихся, прежде всего необходимо ответить на вопрос: а какова его структура?
В науке существует несколько моделей этого психического процесса, описанных в работах известных отечественных и зарубежных психологов (Л. Б. Ительсон, В. А. Крутецкий, Л. К. Максимов, В. Хаекер, Т. Циген). Мы остановили свой выбор на одной из них, базирующейся на исследованиях Ж. Пиаже. Согласно нашим представлениям, психологическая модель структуры математического мышления может быть описана пятью пересекающимися подструктурами, или кластерами.
В зависимости от индивидуальных особенностей любая из них может занимать место доминантной, главной, преобладающей.
Первая из подструктур (назовем ее топологической) помогает нам вычленять в объектах такие математические характеристики, как непрерывно — разрывно, связно — не связно, компактно — не компактно, принадлежит — не принадлежит, внутри — вне, вместе, еди-
ное целое, и оперировать ими. Школьники, у которых доминирует эта подструктура математического мышления, не любят торопиться. Каждое действие они осуществляют очень подробно, стараясь не пропустить в нем ни одного звена. Такие школьники всё проверят, заметят ошибки, они очень логичны и последовательны, их скрупулезность, а отсюда и медлительность порой вызывают раздражение окружающих.
Те, у кого преобладает (доминирует) проективная подструктура, предпочитают рассматривать и изучать любой математический объект с различных точек зрения и позиций, под разным углом, устанавливать соответствие между объектом и его изображением и наоборот (изображением и объектом), искать и находить различные применения и возможности использования предмета в практике, его бытовое назначение и применение, уподоблять его известным объектам. Эти дети поражают нас широтой своего математического мышления, способностью отыскивать и предлагать совершенно неожиданные подходы и аспекты решения.
Сравнивать и оценивать в общем качественном виде (равно — не равно, больше — меньше, ближе — дальше, выше — ниже, над — под, до — после, за) предпочитают те, у кого доминирующей является порядковая подструктура. Вместе с тем для них очень важны форма объектов, их соотношение, направление движения (по или против часовой стрелки, вверх или вниз). Эти юные педанты не позволят нарушить или пропустить ни одного условия, принципа. Действуют они логично, последовательно, по порядку. Работа по алгоритму для них — любимое занятие.
«Метристы» (дети с доминирующей метрической подструктурой) акцентируют свое внимание на количественных характеристиках, «заворожены числом». Главная проблема для них — «сколько?»: какова длина, площадь, расстояние, величина в числовом выражении. Им трудно понять, что ответ может не иметь конкретного количественного значения, они испытывают дискомфорт, если их принуждают к решению в общем (например, буквенном) виде. Для них гораздо приятнее решать задачу по действиям, результатом каждого из которых является число, нежели искать общий принцип, идею.
Наконец, учащиеся с доминирующей алгебраической подструктурой постоянно стремятся к всевозможным комбинациям и манипуляциям, вычленению частей и их сбору в единое целое (единый блок), к сокращению и замене нескольких преобразований одним. Это те самые «торопыги», которые, в противоположность «топологам», не хотят и с огромным трудом заставляют себя подробно прослеживать, записывать, объяснять все шаги решения или обосновывать собственные действия. Эти будущие Остапы Бендеры («великие комбинаторы») думают и делают быстро, способны фонтанировать идеи, предположения и гипотезы решения, но при этом часто и ошибаются.
Доминантная подструктура математического мышления проявляет себя во всех математических действиях, и в зависимости от нее каждый ученик выбирает свой индивидуальный метод решения. Проиллюстрируем это примером решения шестиклассниками с разными доминантными кластерами следующей задачи: «Приходит пастух с 70 быками. Счетчик скота спрашивает его: «Сколько скота приводишь ты из своего стада?» Ему сказано пастухом: «Я привел тебе две трети от трети скота, определи, сколько скота в стаде».
Школьник с доминирующей топологической подструктурой рассматривает все стадо как единое компактное связное целое, внутри которого опять есть единые компактные связные (три) части, а внутри одной из них — 70 быков, составляющих ее неотъемлемую часть.
Графически он интерпретирует ситуацию единой непрерывной линией, внутри которой связно находятся выделенные им части. При этом школьника совершенно не заботит форма линии (отрезок, ломаная, произвольная кривая), что будет очень важно, например, для детей с порядковой доминантой.

70 • 4,5 = 315 (голов).
Дети, у которых наиболее ярко выделена проективная подструктура, проецируют стадо в клетки. Установив соответствие между стадом и клетками и в дальнейшем оперируя графическими заместителями (клетками), они предлагают такое решение:

Школьники, у которых доминирует порядковая подструктура, решают задачу традиционным, обычным способом по действиям.
Дети с доминантной метрической подструктурой («метристы») просто оперируют числами (величинами) — считают:
70 быков — 2/3 от 1/3, значит, 70 • 3/2 = 105 (голов) — 1/3 всего стада, 105 • 3 = 315 (голов).
Учащиеся с ведущей алгебраической подструктурой максимально сокращают («сворачивают») решения и рассуждения и путем логических комбинаций всех данных («частей» условия задачи) составляют уравнение:
х — все стадо, 2/3 • 1/3 • х = 35, 2/9х = 35, х = 315.
Цель обучения математике не только в вооружении учащихся знаниями, умениями и навыками (ЗУН), но и в интеллектуальном развитии, адекватном особенностям математического мышления детей. Не «ломать», а максимально использовать и развивать индивидуальные особенности умственной деятельности школьников — вот в чем заключается дидактическая задача учителя. С этих позиций ЗУНы следует рассматривать как необходимые условия и средство интеллектуального развития детей. Понятно, что далеко не всем учащимся в будущем придется пользоваться логарифмами, составлять уравнения плоскости или сферы, а способность логически рассуждать или доказательно убеждать потребуется каждому. И делать это будет каждый человек не по общей схеме, а в индивидуальной, присущей лично ему манере. Поэтому, подбирая задачи и упражнения к уроку, необходимо наряду с обучающей целью одновременно задаться и вопросом о качестве, способе конструирования рассуждения каждым и, конечно, о той подструктуре мышления, которую посредством этих заданий наиболее удобно и эффективно можно сформировать.
Как показывает наш опыт, продуктивно решать эти проблемы удается на специальных уроках, которые мы называем «уроками одной задачи». Эти уроки интересны тем, что от учащихся не требуется общего, одинакового для всех решения. Каждый может решить задачу тем способом, который ему понятнее, доступнее, убедительнее, а зависит он от доминантной подструктуры математического мышления школьника. В соответствии с ней и помощь учителя, его подсказки разным учащимся должны быть различными.
В этом случае они будут услышаны, восприняты и приняты. Иначе объяснение педагога может оказаться бесполезным, ибо, как утверждал знаменитый И. Гёте: «Каждый слышит только то, что он понимает».
А понимает человек тогда, когда усваивает математические знания или открывает решение в рамках своего кластера, своей доминантной подструктуры мышления.
Психологические исследования показывают, что усвоить иной (не адекватный его подструктуре) способ рассуждения человек может лишь после того, как предварительно овладел своим «родным» (адекватным его кластеру) методом решения проблемы. Отсюда нетрудно сделать вывод о том, что каждую задачу ученик должен сначала решить своим индивидуальным способом и лишь после этого пытаться понять иные методы рассуждений.
Поясним сказанное на примере урока одной задачи по геометрии в IX классе (после вывода формулы нахождения площади треугольника по формуле SD = 1/2 ab • sin а.
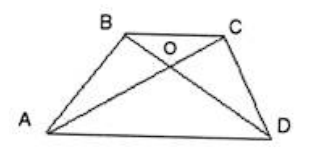
Учащимся предлагается решить задачу: «Трапеция разбита диагоналями на четыре треугольника. Доказать, что треугольники, прилежащие к боковым сторонам, равновелики».
Предварительно класс разбивается на 5 групп (на основе диагностики) по доминантным подструктурам математического мышления: на «топологов», «проективистов», «порядков- цев», «метристов» и «алгебраистов».
Каждой группе предлагается решить предложенную задачу. Роль учителя заключается в том, чтобы в зависимости от доминантного кластера математического мышления детей той или иной группы найти те подсказки, которые окажут им реальную помощь.
Учитывая особенности математического мышления детей с доминантной топологической подструктурой, помощь учителя должна формулироваться им в рамках терминов и понятий типа «внутри», «принадлежит», «часть», «включает», «объединение», «пересечение» (как общее, вместе, связное друг с другом, непрерывно, компактно расположенное). Поэтому естественной подсказкой (вопросом группе «топологов») может быть акцент на использовании принадлежности, включения (внутри) одних треугольников другим, а именно: «Не видите ли вы треугольник, в который включаются ∆АВО и ∆COD?» Обычно этой подсказки оказывается достаточно, чтобы решить задачу.
Если первая подсказка не помогла, то группе предлагается следующая подсказка: площади каких фигур включают в себя площади ∆ABD и ∆ACD? Имеют ли общую площадь ∆ABD и ∆ACD? Что является пересечением ∆ABD и ∆ACD? И т.д.
Обычно «топологи», самостоятельно или используя приведенные подсказки, выстраивают следующее доказательство, опираясь на принадлежность (включение, внутри, связно) одних треугольников другим.
Рассмотрим ∆ABD и ∆ACD. У них общее основание AD и равные высоты на эти основания. Отсюда Sabd = Sacd,
Sabo = Sabd — Saod = Sacd — Saod = Scod.
Поскольку порядковцы ориентируются, прежде всего, на такие отношения как «больше — меньше», «равно», любят действовать последовательно, им предлагаются следующие подсказки.
Диагонали разбили трапецию на несколько треугольников. Установите последовательность величин их площадей от большего к меньшему. Есть ли среди них треугольники с равными величинами площадей? На основании чего вы можете заключить, что площадь каждого последующего треугольника убывает? Попробуйте последовательно заменять площадь трапеции суммой площадей больших треугольников, их суммой площадей маленьких треугольников. Разные дети после разного количества подсказок (кто-то раньше, кто-то позже) приходят примерно к следующему решению:
Sabcd = Sabd + Sbcd, но Sabd = Sacd, значит Sabcd = Sacd + Sbcd.
Далее, последовательно заменяя площади больших треугольников площадями более маленьких, их составляющих, они получают:
Sabo + Sbco + Scod + Saod = (Saod + Scod) + (Sboc + Scod), откуда Sabo = Scod.
Метрическая подструктура акцентирует внимание человека на количественных преобразованиях и позволяет пересчитывать, определять конкретные числовые значения. Естественной подсказкой группе «метристов» является следующая: по известной формуле S∆ = 1/2 ab • sin а вычислите площади ∆АВО и ∆COD, использовав подобие ∆ВОС и ∆AOD.
Решение «метристов»: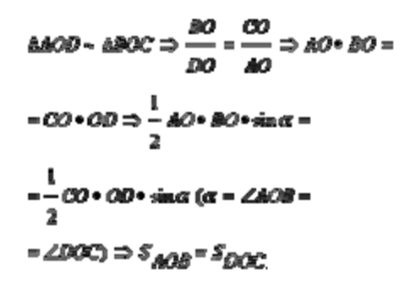
Проективная подструктура позволяет изучать математический объект путем установления соответствия между этим объектом и его различными проекциями. Следовательно, «проективистам» очевидной и полезной будет подсказка, предлагающая заменить («спроецировать») треугольники на одну из сторон — отрезки диагоналей трапеции. После того как учитель предложит этой группе заменить отношение площадей треугольников с одинаковыми высотами (∆АВО и ∆ВОС, ∆ВОС и ∆OCD) отношением оснований, используя подобие треугольников, они легко приходят к следующему решению.
Рассмотрим ∆АВО и ∆ВОС. Для них можно записать:?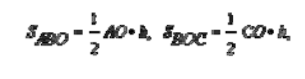
откуда следует, что
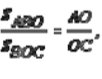
Аналогично получаем равенство:
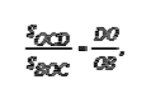
а из подобия ∆ВОС и ∆AOD следует, что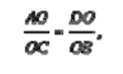
Значит,
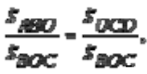
Откуда
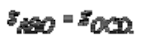
Наконец, алгебраическая подструктура позволяет осуществлять не только прямые, но и обратные операции, легко переключаться с прямых действий на противоположные, заменять несколько операций одной, вычленять части и собирать их в единое целое и т. д. Поэтому эффективными подсказками учителя будут 1) использовать метод от противного или 2) провести через точку О отрезок MN || ВС и воспользоваться ранее доказанным фактом о том, что МО = ON. Такие действия помогают группе с этой доминантной подструктурой решить задачу следующим образом.
1-й способ.
Допустим, что Sabo + Scod, тогда
SABD ï SACD ^ BC || AD, получили противоречие тому, что ABCD — трапеция. Значит, допущение неверно и Sabo = Scod.
2-й способ.
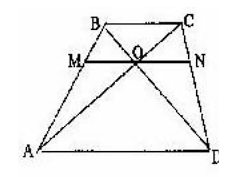
Разобьем рассматриваемые ∆АОВ и ∆COD на части. Для этого проведем
MN || ВС. МО = ON (по ранее доказанному). Получаем, что ∆АОВ и ∆COD состоят из двух треугольников, площади которых равны. Samo = Sdon, Smbo = Socn. Следовательно, Sabo = Scbd.
Каждая группа выступает со своим доказательством. Это очень важный этап урока, так как лишь после того, как школьник усвоил решение, адекватное своему кластеру, он способен осознанно и неформально овладеть иными способами решения, базирующимися на других подструктурах математического мышления. Таким образом, обучение начинает строиться в зоне ближайшего развития, которая рассматривается в двух аспектах.
С одной стороны, нетрадиционном — развитие других, недоминантных подструктур математического мышления, которое происходит при усвоении детьми
других методов решений. С другой — традиционном. Это достигается предложением школьникам решить более сложные задачи с учетом уже решенной.
Например:
Задача № 2.
Докажите, что медианы разбивают треугольник на 6 равновеликих треугольников.
Задача № 3.
Дана трапеция ABCD, ВС || AD, Sboc = S1, Saod = S2. Найдите площадь трапеции.
Коллективное обсуждение в группах приводит детей к решению задач.
Описанный подход к решению математических задач, во-первых, способствует непроизвольному развитию слаборазвитых подструктур мышления, во-вторых, нивелирует боязнь неуспеха, страх перед задачей, в-третьих, повышает самооценку в данном виде деятельности. Наблюдается заметное развитие потенциальных возможностей школьников в математической деятельности (и не только в ней), реализация ими своих потребностей и интересов. Вместе с тем описанный метод обучения решению задач вполне можно считать гуманизированным. Данный метод обучает школьника тому, что он не умеет, не путем многократных упражнений на действия, которые у него «западают» (а потому, естественно, вызывают негативную реакцию и мотивацию), а посредством операций, которые у него получаются, легко выполняются и которые, стало быть, он реализует с удовольствием.
Информация об авторах
Метрики
Просмотров
Всего: 2716
В прошлом месяце: 8
В текущем месяце: 21
Скачиваний
Всего: 1345
В прошлом месяце: 3
В текущем месяце: 9