Психологическая наука и образование
2024. Том 29. № 1. С. 87–98
doi:10.17759/pse.2024290107
ISSN: 1814-2052 / 2311-7273 (online)
Возможности опосредствования решения арифметических задач третьеклассниками: процедура «комплектования»
Аннотация
Представлены материалы исследования, направленного на объективацию типичных затруднений, испытываемых учащимися при выполнении даже простейших расчетов, связанных с согласованными преобразованиями величин. Разработанные нами задачи, решение которых требовало учета «комплектности» величин из условий, предлагались 97 третьеклассникам трех общеобразовательных школ Москвы в форме индивидуальной письменной работы. Из их числа случайным образом были составлены 25 пар, совместно решавших аналогичную задачу в устном собеседовании с экспериментатором. Анализ результатов выявил беспомощность большей части обследованных учащихся в решении подобных задач. Подробное рассмотрение письменных решений и протоколов собеседования позволило охарактеризовать модельные средства, используемые учащимися, как формальные или конструктивные (порционное отмеривание разнородных величин). Показано, что источником трудностей в решении задач, связанных с комплектованием, является отсутствие у большинства детей способов их адекватного модельного опосредствования. В целом подтвердилась актуальность рассмотрения «задачи комплектования» в общей линии развития понятия числа в начальном обучении математике в рамках концепции учебной деятельности В.В. Давыдова.
Общая информация
Ключевые слова: обучение математике, начальная школа, опосредствование, комплексная модель, качество образования
Рубрика издания: Психология образования
Тип материала: научная статья
DOI: https://doi.org/10.17759/pse.2024290107
Получена: 26.07.2023
Принята в печать:
Для цитаты: Лобанова А.Д., Высоцкая Е.В. Возможности опосредствования решения арифметических задач третьеклассниками: процедура «комплектования» // Психологическая наука и образование. 2024. Том 29. № 1. С. 87–98. DOI: 10.17759/pse.2024290107
Полный текст
Введение
«…И вот я сидел и смотрел на них: у мальчика
два кармана, у девочки один карман, – и у меня
в голове стали появляться какие-то проблески…»
Н. Носов. «Витя Малеев в школе и дома»
Актуальность выявления путей оптимизации обучения младших школьников решению задач, требующих координации действий с разнородными величинами, вряд ли может быть переоценена. Теоретический анализ оснований для возникновения соответствующих мыслительных новообразований, начатый еще Ж. Пиаже [14], продолжается и в современных исследованиях [8; 13; 15; 17; 20; 23]. Во многих работах указывается на наличие постоянно воспроизводящихся затруднений детей в решении таких задач. Это, на наш взгляд, подчеркивает объективную сложность конструирования особого типа учебных ситуаций, в основу которых была бы заложена необходимость согласования действий, связанных с изменениями величин.
Существенное продвижение в исследовании специфики этой особой «предметности» математики начальной школы было в свое время достигнуто разработками в области психологии обучения математике [1; 5; 12; 19; 21], опирающимися на содержательно-деятельностное рассмотрение психологических механизмов формирования понятия числа в работах В.В. Давыдова [2; 11]. Задача комплектования стоит особняком среди первых задач курса начальной математики. Она рассматривалась прежде всего как форма сравнения предметных совокупностей, входящая в противоречие с непосредственным подсчетом отдельных предметов, их образующих. Освоение сложных процедур отсчитывания «порций» объектов по образцу и пересчета самих «порций», восходящих к содержанию практико-предметной ситуации комплектования, рассматривалось В.В. Давыдовым как особая учебная задача, решение которой имеет большое значение для полноценного формирования понятия числа в дальнейшем [2, с. 58-66; 3, с. 180-188]. Задача на «опосредствованное» сравнение, необходимое при оценке достаточности количества составляющих для «комплектов», проявляла характер ориентировки, складывающейся у ребенка: «содержательный» (когда сравнение, то есть определение «чего больше?» в наглядно представленных предметных совокупностях было опосредовано комплектом-образцом) или же «формальный» (если сравнение множеств ограничивалось пересчетом отдельных предметов) [11, с. 145-147]. Противоречие «наглядного» и «понятийного» в условиях задач вскрывало определенные дефициты навыков счета, усвоенных первоклассниками.
Исследование потенциала особой предметности задачи комплектования [16; 22] как пропедевтической в общей линии формирования понятия числа у младших школьников может быть актуальным и в настоящее время.
Организация, процедура и методы исследования
Представляемое здесь исследование, соответственно, имело своей целью объективацию типичных затруднений, сохраняющихся у учащихся в решении текстовых арифметических задач, прямо или косвенно связанных с процедурами комплектования и задаваемыми ими отношениями величин. С такими задачами учащиеся начальной школы сталкиваются в третьем–четвертом классе [7]. Для оценки возможностей третьеклассников в выполнении согласованных преобразований величин были составлены две задачи «про кукол и пуговицы», которые требовали от учащихся (среди прочих простых расчетов) отмеривания «комплектующих» для явно или неявно заданного числа комплектов. В первой части обследования проводилась индивидуальная письменная работа – ответ на два простых «прямых» вопроса первой задачи:
Задача 1. Маша шьет кукол, у которых глаза будут из синих пуговиц. К каждому платью она пришьет 3 зеленые пуговицы.
(Вопрос 1) Сколько ей надо будет взять синих пуговиц, если она уже пришила 12 зеленых пуговиц?
(Вопросы 2а и 2б) Если у Маши будет 10 синих пуговиц, сколько она сможет сделать таких кукол, и сколько зеленых пуговиц ей тогда понадобится?
Для второй части обследования (устного собеседования с каждой парой учащихся, работающих совместно) задача была составлена так, чтобы ответы на вопросы не могли быть получены простым повторением образца комплекта пуговиц. Ее новое содержание составила ситуация «нехватки» обеих комплектуемых величин:
Задача 2. Маша придумала шить кукол: их глаза будут из синих пуговиц, а на каждое платье она пришьет три зеленых пуговицы. Она решила сшить восемь таких кукол и отсчитала для них столько пуговиц, сколько нужно. Когда она пришла в школу, в кармане у нее оказалось 14 зеленых пуговиц и 13 синих.
(Вопрос 1) Сколько кукол выйдет теперь у Маши-растеряши?
(Вопрос 2) Сколько пуговиц растеряла Маша, идя в школу?
Объединение учащихся в пары было необходимо для того, чтобы экспериментатор мог зафиксировать развернутый процесс решения задачи и характер использования ими предлагаемого счетного материала, частично озвучиваемый детьми в процессе их обсуждения друг с другом при совместном решении.
В первой части (индивидуальное письменное решение задачи) приняли участие 97 третьеклассников трех общеобразовательных школ города Москвы (43 мальчика и 54 девочки, 9-10 лет). Для второй части (совместное устное решение задачи аналогичного содержания) из их числа было случайным образом выбрано 50 учащихся (всего было проведено 25 собеседований с учащимися, объединенными в пары).
При выполнении индивидуальных заданий первой части учащиеся могли записать свои рассуждения в любой удобной для них форме. Время выполнения заданий не было ограничено. В среднем на индивидуальное решение детям требовалось 10 минут. Для решения второй задачи каждой паре учащихся выдавался общий бланк с условием задачи и счетный материал (фишки синего и зеленого цвета) для совместного использования. Собеседование завершалось, когда учащиеся считали свое решение законченным, и продолжалось от 7 до 17 минут.
В качестве материала для анализа были использованы письменные работы, протоколы и видеозаписи собеседований.
Количественный анализ включал в себя подсчет доли верных ответов и анализ связи успешности решения вопросов письменного задания между собой с помощью таблиц сопряженности. Расчет критерия χ2 (хи-квадрат) производился в статистическом пакете jamovi 2.3.28.
Обсуждение результатов
Общая успешность решения первой задачи составила 54%. Доля (в процентах) учеников, верно ответивших на каждый из вопросов, представлена в табл. 1.
Таблица 1. Успешность индивидуального письменного решения первой задачи третьеклассниками
|
Вопросы первой задачи |
Доля учеников (в процентах), давших верный ответ |
|
Вопрос 1: Сколько нужно синих пуговиц, если использовано 12 зеленых? |
39 |
|
Вопрос 2а: Сколько кукол получится сшить? |
67 |
|
Вопрос 2б: Сколько зеленых пуговиц потребуется, если использовано 10 синих? |
56 |
Подсчет значимости различий между успешностью решения вопроса 1 и вопросов 2а и 2б произведен с использованием таблиц сопряженности. Из анализа следует:
1) значимая прямая связь между правильностью ответов на вопросы 2а и 2б (χ2=47,3, р<0,0001);
2) значимая прямая связь между правильностью ответов на вопрос 1 и 2а (χ2=10,8, р=0,001);
3) нет связи между правильностью ответов на вопрос 1 и 2б (χ2=1,26, р>0,05).
Отметим, что среди 13 детей, которые правильно ответили про кукол во втором вопросе (2а), но не смогли посчитать пуговицы (зеленые, вопрос 2б), не оказалось ни одного, кто правильно ответил бы и на первый вопрос.
Разброс успешности решений позволил выделить пять групп, объединивших тех, кто:
- не решил ничего (21 человек);
- верно ответил на все вопросы (28 человек);
- ответил верно только на вопрос 2а про кукол (13 человек);
- правильно ответил на вопросы 2а и 2б, но не ответил на вопрос 1 (24 человека);
- правильно ответил только на первый вопрос (8 человек).
Другие варианты сочетания верных и неверных решений составили 3 работы из 97.
Значительное число учеников, у которых формально правильные ответы на одни вопросы сочетались с неправильными ответами на другие, заставило нас обратить особое внимание на содержание записей, дополняющих арифметические расчеты. В 68 из 194 решений содержались краткие записи условия, таблицы, в которые дети вписывали количество пуговиц и кукол из условия, и рисунки рядов пуговиц или кукол с пуговицами. О связи успешности решений учащихся с использованием ими определенных средств свидетельствуют данные, приведенные в табл. 2. Успешность решения задач оказалась значимо связана с типом записей, использованных учениками (χ2=22, р<0,001).
Таблица 2. Успешность решений первой задачи для разных вариантов «дополнительных» записей, сделанных третьеклассниками
|
Записи, сопровождающие решения |
Количество верных ответов |
Количество неверных ответов |
«Эффективность» использования записей (доля правильных ответов в процентах)* |
|
Краткая запись условия (9 работ) |
4 |
5 |
44 |
|
Табличная запись (16 работ) |
6 |
10 |
38 |
|
Изображения пуговиц, объединенных в порции (29 работ) |
23 |
6 |
79 |
|
Изображения пуговиц рядами без выделения порций (14 работ) |
1 |
13 |
7 |
|
Ничего из перечисленного (126) |
56 |
70 |
44 |
Примечание. * доля правильных ответов в работах с такой записью.
Краткие записи условия обнаружены в работах шести учащихся: четыре решения оказались верными (рис. 1а), а пять – неверными (рис. 1б, в).
Рис. 1. Примеры кратких записей условия, сопровождающих верное (а) и неверные (б и в) решения
Табличная запись была использована лишь 13 учениками одного из обследованных классов. Очевидно, что ученики, которые составляли таблицы, были обучены именно этому типовому приему представления условий задач. Рис. 2 иллюстрирует примеры как успешного (рис. 2а), так и неуспешного использования ими таких «опор» (рис. 2б).
Рис. 2. Примеры решений с использованием таблицы: а) верное; б) неверное
Все встреченные нами изображения кукол и пуговиц можно было разделить на две группы: те, в которых пуговицы были отчетливо распределены «комплектами» (рисунки кукол с пуговицами, пуговицы, обведенные по парам и тройкам), и те, которые не обнаружили следов «порционного» пересчета (ряды пуговиц по числу их в условии, куклы без пуговиц).
Изображение пуговиц порциями чаще всего сопровождалось верными (рис. 3а) арифметическими действиями и ответами (23 из 29 ответов).
Рис. 3. Примеры изображений порций пуговиц, сопровождающих верное (а) и неверное (б) решения
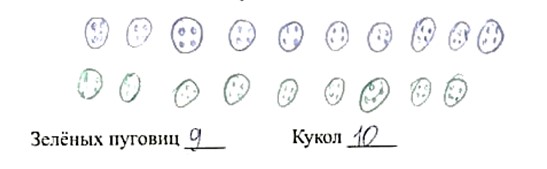
Изображение пуговиц рядами или кучками (рис. 4) встречалось нечасто (14 рисунков). Среди решений, иллюстрированных таким образом, было всего одно правильное (пример: рис. 4а).
Рис. 4. Примеры изображений пуговиц без группировки по порциям, сопровождавшие правильный (а) и неправильный (б) ответы
Во второй части более трети учащихся, работавших парами (36%), не справились ни с одним вопросом второй задачи. При этом на первый вопрос задачи (сколько кукол получится сделать?) ответили 60%, а на второй вопрос (сколько пуговиц было потеряно?) – только 28% учащихся.
Анализ протоколов устного собеседования во второй части позволил выявить три группы учащихся, различающихся по реализуемым «стратегиям» поиска решения и соответственно по успешности решения задачи второй серии.
К первой группе (9 протоколов, 18 учащихся) мы отнесли тех, кто не смог ответить ни на один вопрос (не определили количество кукол, которые можно сшить из оставшихся пуговиц, и не посчитали, сколько пуговиц было потеряно). Все их решения сводились к произвольным манипуляциям с числами, взятыми из условия или полученными по ходу расчетов. Приведем примеры таких решений.
Ученица А.: «9 плюс 8… это 17... это она сшила еще 8 платьев – это 8. А еще 14 плюс 13 – это 27. 27 делить на 3 равно 9».
Ученики М. и Л.:
М. (делит 8 на 4): 2 пуговицы потеряла...
Л.: Не могла она две пуговицы потерять. Тогда бы ей не хватило на восемь кукол. Смысл ей терять две пуговицы?
М.: Может, четыре умножить на…
Л.: На восемь? 32 пуговицы, что ли?
М.: У нее в кармане столько бы не поместилось просто…
Л.: Смешно… Наверное, нужно все-таки восемь разделить на четыре.
М.: Но она же не могла две пуговицы потерять. Смысл ей их брать, если она все равно не сможет из них сшить куклу…
Ученица В. (объясняет, почему она сначала хотела вычесть из трех восемь): Я думала, что там «минус» будет первое действие, потому что… у нее вот было три зеленых пуговки, она решила сшить… А когда они сшивают… они же уменьшаются! Они же на кукле становятся. Ну вот, пишут… «А на каждое платье пришивать три зеленых»!.. А!.. Пришивать – так это «деление»...
Показательно, что при этом дети не обращались к счетному материалу, подготовленному на столах, по своей инициативе: даже если им предлагалось решить задачу с его помощью, они отвечали, что «это только путает». Только одна пара учащихся смогла последовательно построить верное решение для второго вопроса без опоры на работу со счетным материалом, но не справилась с первым, более «легким» вопросом.
Вторая группа включала 9 пар учеников, которые ответили верно на первый вопрос, но не справились со вторым вопросом задачи (о том, сколько пуговиц было потеряно). При обращении к счетному материалу учащиеся этой группы верно отделили порции «пуговиц» и ответили на первый вопрос. Однако затем они считали «не те» пуговицы – например, лишние пуговицы из тех, что не были потеряны, или пуговицы для четырех кукол, которых не получилось сделать, и т.п.: раскладывание и пересчитывание взятого счетного материала приводило их к неверным ответам. Приведем примеры такой работы:
Ученик Я. (выкладывает восемь синих бумажек перед собой): Мы берем восемь кукол (обводит рукой бумажки), и на каждую куклу по два глаза… (отделяет бумажки парами). Получаются четыре куклы.
Ученики Ю. и Л. собирают четыре нужных «комплекта» из 14 зеленых и 13 синих «пуговок» и пересчитывают оставшиеся при этом пуговицы.
Ю.: Все. Она потеряла две зеленых и еще 1-2-3-4-5 (считает пальцем) – пять синих.
Правильному же подсчету числа «потерянных» пуговиц (6 протоколов) способствовало исключительно «порционное» выкладывание заданного (рис. 5). Некоторые ученики начинали с того же формального перебора арифметических действий, но затем все-таки обращались к решению с помощью выданных «пуговок» и получали правильный ответ, который они могли обосновать друг другу и экспериментатору:
Ученики М. и Ф.:
М.: Ну-у… (показывает на условия и читает их). Она решила сшить 8 точно таких же… То есть 8 – это по три и по два (показывает на выложенные «пуговицы»). 24 получается пуговицы, а тут, когда она пришла в школу, у нее оказалось 14, значит… 10. И еще три потеряла… ой… я запутался что-то… (тихо) я никогда такого не делал…
Ф.: У нее было (считает) 16 синих, а потеряла 3…
М.: Она 10 потеряла, осталось 14.
М.: 12… 15… и минус один… 14 (выложено пять троек зеленых «пуговиц» и из последней тройки отодвинута одна «пуговка»). И у нее было 16 синих глаз. Она потеряла 3. (Прикладывают по паре синих «пуговиц» к каждой тройке зеленых – получается 4 «комплекта». Двигают еще одну пару из оставшихся синих «пуговок» к двум зеленым «пуговкам» из неполной тройки.)
М.: То есть 1-2-3-4-5 (пересчитывает «кукол»)…
Ф. (перечитывает вопрос): Вот эта не выйдет! (показывает на последнюю). Потому что там написано: три! Не две и не одна. То есть 1-2-3-4… куклы!
М.: Просто вникнуть надо было!
Рис. 5. Процесс решения задачи с помощью выкладывания «пуговиц» порциями (две синих «пуговицы» для «глаз» и три зеленых – для платья куклы)
Результаты проведенного обследования продемонстрировали ряд особенностей использования третьеклассниками типичных приемов построения решения предложенных нами задач. Число и характер допущенных ошибок свидетельствуют, на наш взгляд, о выраженной беспомощности части обследованных третьеклассников в подборе и выполнении хорошо известных им операций с целыми числами в пределах первых четырех десятков.
Обобщая полученные результаты, следует отметить, что явные различия между успешностью в ответах на первый и второй вопросы письменной части (39% правильных решений против 56%) и в ответах на первый и второй вопрос в устном собеседовании (60% правильных решений против 28%) с очевидностью связаны с тем, что величины, необходимые для расчетов, в соответствующих вопросах были заданы косвенно. Например, в письменном обследовании четверть учащихся (24 третьеклассника) не справились с первой задачей, в которой «вспомогательная» величина (число кукол) была скрыта, но решили вторую, в которой требовалось именно эту величину найти. Показательно и то, что все 13 человек, которым даже верно найденное количество кукол не помогло отсчитать необходимые пуговицы, не справились с таким расчетом при ответе на первый вопрос, где «подсказка» про подсчет кукол отсутствовала.
Разрыв в количестве правильных ответов на вопросы устного собеседования свидетельствует об объективной сложности работы в заданной предметной ситуации: первый вопрос (про кукол) указывал на необходимость «прямого» исчерпывания заданных количеств синих и зеленых пуговиц нужными порциями, тогда как второй вопрос (отсчет потерянных пуговиц) требовал их предварительного «порционного» отмеривания для восьми кукол исключительно лишь в качестве посредника решения.
Среди использованных учениками типовых «вспомогательных» записей эффективным средством показала себя только рисуночная схема пуговиц, сгруппированных порциями для каждой куклы (79% правильных решений). Успешность решения задач с использованием простой и табличной краткой записи практически не отличалась от успешности решения задач вообще без каких-либо пояснений к составленным выражениям и ответам (44% и 38% против 44% соответственно, χ2=0,28, p>0,05). Наличие же нарисованных кукол без пуговиц или рядов пуговиц без видимого разделения их на порции было значимо связано с неверными ответами (χ2=7,26, р<0,01). Это можно рассматривать как косвенное свидетельство содержательности посреднической роли рисуночной схемы в построении решения в отличие от табличной и краткой записи условий, которые можно рассматривать здесь как исключительно «формальные».
Устное собеседование во второй серии позволило нам уточнить особое содержание предметного действия, связанного с использованием рисуночной схемы, дающей значимые преимущества в успешности решения задач. Счетный материал, который предлагался учащимся, сам по себе не гарантировал выполнения им модельных функций в отношении анализа предметной ситуации задачи. Однако он вполне подходил для того, чтобы использовать его в этом качестве, позволяя «материализовать» неявно заданную «третью» величину (число порций пуговиц), от которой впрямую зависело решение. Это и давало решающим потенциальную возможность выполнить адекватное ориентировочное действие (объединение разных пуговиц в комплекты в соответствии с требуемым числом кукол), опосредующее все требуемые расчеты, и принять во внимание как явно, так и неявно заданные условия.
Те третьеклассники (6 пар из 25), которые успешно решили всю задачу, раскладывая счетный материал на порции, по всей видимости, наделяли его требуемой модельной функцией. Неверные же ответы были связаны именно с попытками «напрямую» извлечь готовое решение из подсчетов «пуговиц», разложенных ими на столе случайным образом. Только те учащиеся, которые начинали раскладывать выданные им «пуговицы» порциями, смогли найти и исправить ошибки, сделанные ими в начале, и благодаря этому все-таки справились хотя бы с первым вопросом. Обращение испытуемых к объективно необходимым здесь действиям по согласованному отсчету порций, проявляющим неявно заданное отношение рассчитываемых величин, по всей видимости, и позволяло им преодолеть затруднения «простого пересчета» при решении таких задач.
Выводы
Полученные нами результаты подтверждают наше предположение о важнейшей роли модельных действий, непосредственно связанных с процедурами комплектования, в решении предлагавшихся задач. Именно отсутствие уверенного владения такими действиями заставляет учащихся выбирать «обходные пути» даже в простейших расчетных задачах: их место занимает случайный подбор чисел и операций с ними.
Предложенные нами задачи требовали именно точного подсчета и согласования независимых изменений разнородных величин, увязанных между собой сюжетом (строением предметной ситуации). Средством учета согласования изменений величин здесь является отмеривание каждой из них порциями согласно образцу и определение числа таких порций в соответствии с нужным числом объектов, для которых они предназначены (в нашем случае кукол, для которых требовались пуговицы двух сортов). Определение этой «третьей» величины, явно или неявно присутствующей в условиях задач, играет главную ориентировочную роль в определении порядка действий и использовании арифметических операций при их решении.
Продемонстрированные детьми способы применения как собственных, так и предложенных вспомогательных средств (схем, рисунков, счетного материала) выявили возможные основания беспомощности некоторых учащихся в решении «критических» задач, в которых данные условия не могли быть непосредственно использованы для получения ответа. Проделанные ими вычисления можно квалифицировать как «формальные»; лишь «содержательный» способ подразумевал бы включение вспомогательного материала и действий с ним как «модельных», но для третьеклассников возможность такого его использования не была очевидной. Известные им приемы поиска «нужных» операций по условию (как например, составление таблиц) никак не помогали найти правильный ответ. Модельная же реконструкция предметной ситуации, позволившая бы ученикам спроектировать собственное решение с учетом неявно заданных условий (определить порядок арифметических действий), явно не составляла предмет предшествовавшего обучения.
Необходимо отметить, что попытки рассмотрения типичных детских ошибок в решении простейших расчетных задач закономерно, на наш взгляд, приводят исследователей к анализу «дефицитов» использования «модельных опор» и возможностей их деятельного освоения учащимися начальной школы [9; 10; 11; 19]; отношение к модельным объектам лишь как к «наглядному», иллюстративному материалу подвергалось в свое время содержательной критике [3; 4], но, к сожалению, проявляется в методической поддержке начального обучения до сих пор.
В целом результаты проведенного исследования, как и многих других в этом направлении [6; 19; 20], подтверждают актуальность психолого-дидактического исследования возможностей встраивания в начальный курс математики особого предметно-модельного содержания, востребованного в связи с соизмерением независимых величин в задачах «на комплектование». Значительные перспективы здесь открывают логико-генетический анализ состава действий, непосредственно связанных с освоением учащимися такого учебного материала, и определение структуры и функций необходимого модельного опосредствования в рамках общей линии психологического исследования формирования понятия числа в начальной школе.
Литература
- Александрова Э.И. Математика. 1 класс. Учебник. Книга 1. М.: БИНОМ. Лаборатория знаний, 2019. 160 с.
- Давыдов В.В. Анализ строения счета как предпосылка построения программы по арифметике // Вопросы психологии учебной деятельности младших школьников. М.: АПН РСФСР, 1962. С. 50–184.
- Давыдов В.В. Виды обобщения в обучении. М.: Педагогика, 2000. 480 с.
- Давыдов В.В., Варданян А.У. Учебная деятельность и моделирование. Ереван: Луйс, 1981. 220 с.
- Давыдов В.В., Горбов С.Ф., Микулина Г.Г. Математика. 1 класс. Учебник. ФГОС. М: Просвещение/Бином, 2022. 160 с.
- Лобанова А.Д., Высоцкая Е.В., Янишевская М.А. Встроенная диагностика модельного опосредствования у учащихся начальной школы: задача комплектования // Деятельностная педагогика и педагогическое образование: Сборник докладов участников IX и X Международных конференций ДППО-2021 (г. Воронеж, 10–14 сентября 2021 г.); ДППО-2022 (г. Воронеж, 9–13 сентября 2022 г.) / Под ред. А.В. Боровских. М.: МАКС Пресс, 2022. С. 66–72.
- Математика. 3-й класс. Учебник. В 2 частях. Ч. 2 / М.И. Моро [и др.]. М.: Просвещение, 2023. 112 с.
- Рубцов В.В. Организация совместных действий и развитие интеллекта у детей // Совместная учебная деятельность и развитие детей. Коллективная монография. Глава 3 / Под ред. В.В. Рубцова, И.М. Улановской. М.: ФГБОУ ВО МГППУ, 2021. C. 48–69.
- Чудинова Е.В. Инициативная опора школьников на схемы в самостоятельном решении задач // Психологическая наука и образование. 2021. Том 26. № 2. С. 66–77. DOI:10.17759/pse.2021260206
- Эльконин Б.Д. Современность теории и практики Учебной Деятельности: ключевые вопросы и перспективы // Психологическая наука и образование. 2020. Том 25. № 4. С. 28–39. DOI:10.17759/pse.2020250403
- Эльконин Д.Б., Давыдов В.В. Возрастные возможности усвоения знаний. М.: Просвещение, 1966. 442 с.
- Coles A. Commentary on a special issue: Davydov’s approach in the XXI century // Educational Studies in Mathematics. 2021. 106(3). P. 471–478. DOI:10.1007/s10649-020-10018-9
- Hilton A., Hilton G. Primary school teachers implementing structured mathematics interventions to promote their mathematics knowledge for teaching proportional reasoning // Journal of Mathematics Teacher Education. 2019. 22(6). P. 545–574. DOI:10.1007/s10857-018-9405-7
- Inhelder B., Piaget J. The growth of logical thinking from childhood to adolescence: An essay on the construction of formal operational structures // Developmental Psychology. Psychology Press. 1958. Vol. 22. 356 p. DOI:10.1037/10034-000
- Lamon S.J. Teaching fractions and ratios for understanding: Essential content knowledge and instructional strategies for teachers. Routledge, 2020. 294 p. DOI:10.4324/9780203803165
- Lobanova A., Rekhtman I., Vysotskaya E., Yanishevskaya M. Towards Proportionality within Developmental Instruction Approach: The First Steps // Mathematics and Its Connections to the Arts and Sciences (MACAS) 15 Years of Interdisciplinary Mathematics Education. Mathematics Education in the Digital Era, vol 19. / Michelsen C. et al. (eds.). Springer, Cham, 2022. P. 205–229. DOI:10.1007/978-3-031-10518-0_11
- Lobato J., Ellis A. Developing Essential Understanding of Ratios, Proportions, and Proportional Reasoning for Teaching Mathematics: Grades 6–8. Reston: National Council of Teachers of Mathematics, 2010. 88 p.
- Polotskaia E., Savard A. Some multiplicative structures in elementary education: A view from relational paradigm // Educational Studies in Mathematics. 2021. Vol. 106. P. 447–469. DOI:10.1007/s10649-020-09979-8
- Polotskaia E., Fellus O.O., Cavalcante A., Savard A. Students’ problem solving and transitioning from numerical to relational thinking // Canadian Journal of Science, Mathematics and Technology Education. 2022. Vol. 22(2). P. 341–364. DOI:10.1007/s42330-022-00218-1
- Simon M.A. Developing a concept of multiplication of fractions: building on constructivist and sociocultural theory // Constructing Number: Merging Perspectives from Psychology and Mathematics Education, Research in Mathematics Education / Norton A., Alibali M.W. (eds.). Springer, Cham, 2019. P. 193–212. DOI:10.1007/978-3-030-00491-0_9
- Venenciano L., Polotskaia E., Mellone M., Radford L. An introduction to multiple perspectives on Davydov’s approach in the XXI century // Educational Studies in Mathematics. 2021. Vol. 106. P. 323–326. DOI:10.1007/s10649-021-10040-5
- Vysotskaya E., Lobanova A., Rekhtman I., Yanishevskaya M. The challenge of proportion: does it require rethinking of the measurement paradigm? // Educational Studies in Mathematics. 2021. Vol. 106(3). P. 429–446. DOI:10.1007/s10649-020-09987-8
- Watson A., Jones K., Pratt D. Key ideas in teaching mathematics: Research-based guidance for ages 9-19. Oxford University Press, 272 p.
Информация об авторах
Метрики
Просмотров
Всего: 317
В прошлом месяце: 29
В текущем месяце: 32
Скачиваний
Всего: 217
В прошлом месяце: 18
В текущем месяце: 31