Математические аспекты концепции адаптивного тренажера^*

Представлена концепция адаптивного тренажера, предназначенного для использования в процессе электронного обучения и обеспечивающего выбор заданий с помощью параметрических вероятностных моделей. Данный подход является альтернативой адаптивным технологиям на базе современной теории тестирования (Item Response Theory). Особенностями диагностических методов, используемых при выборе предъявляемых заданий, являются учет временной динамики изменения способности справляться с заданиями и времени, затрачиваемого на выполнение заданий, а также меньшее по сравнению с другими подходами число заданий, которое следует предъявлять во время тренировки.

1. Введение

В последние годы выросла популярность электронного обучения, охватывающего, в широком смысле, практически все формы и способы передачи знаний, умений и навыков с помощью информационных и коммуникационных технологий. Этот подход к обучению имеет как известные преимущества, так и недостатки, наиболее значимые из которых обусловлены отсутствием эффективной адаптации учебного процесса к индивидуальным особенностям и возможностям его участников. Проблемы, связанные с адаптацией такого рода, сложны для решения и наиболее актуальны при обучении неформализуемым умениям и навыкам, включая решение математических, технических, алгоритмических, изобретательских и других близких по характеру задач.

В случае традиционного обучения эти проблемы обычно преодолеваются путем взаимодействия с квалифицированным преподавателем, который, учитывая известные ему особенности своих учеников, формирует для них индивидуальные траектории обучения, контролируя учебный процесс на всех его этапах. Такая работа, как правило, не поддается автоматизации и является своего рода искусством. Следует отметить, что указанное построение индивидуальных траекторий требует в той или иной форме решения диагностических задач, которые обеспечивают выявление особенностей и возможностей обучающихся.

Задача автоматизации адаптивного обучения неформализуемым умениям и навыкам к настоящему времени не имела удовлетворительного решения. Существующие средства организации электронного обучения [1С: Электронное обучение; Ebmodo [Электронный ресурс]; Kats, 2013; Moodle open-source learning; Wolfram Alpha Webservice], включая системы управления обучением и учебным контентом, обходят рассматриваемую проблему, решая более доступные задачи. Причина этого заключается, в первую очередь, в трудностях формализации и отсутствии подходящего математического аппарата.

В этой работе предложен один из подходов к решению данной задачи, опирающийся на ранее разработанную авторами концепцию адаптивного тестирования, основанную на использовании обучаемых структур в форме марковских процессов [2-4; 6; 10; 11]. Данный подход является альтернативой адаптивным технологиям на базе так называемой современной теории тестирования (Item Response Theory – IRT)¹. В ее основе лежит модель Г. Раша [Baker, 2001; Rasch; Wright, 1982], которая предполагает, что вероятность правильного ответа определяется разностью уровня знаний или способностей испытуемого и трудности тестового задания. Применение этих технологий приводит к следующим проблемам:

– «статичности» оценок: игнорированию того факта, что результат тестирования вследствие усталости испытуемых и других факторов может, вообще говоря, существенно изменяться со временем;

– невозможности учета времени, затрачиваемого на выполнение заданий, при построении расчетных оценок;

– необходимости выполнения достаточно большого числа заданий для получения оценок с приемлемой точностью;

– сравнительно сложной для практического использования процедуре оценки надежности результата.

Перечисленные проблемы сделали актуальной разработку новых технологий. Как один из способов решения этой проблемы далее представлена концепция адаптивного тренажера на базе вероятностной модели для обучения неформализуемым умениям и навыкам, необходимым для решения математических и других задач достаточно высокой сложности, требующих владения как стандартной техникой построения рассуждений, так и элементами творческого мышления. Особенностями диагностических методов, используемых при выборе предъявляемых заданий, являются:

− выявление и использование при построении расчетных оценок временной динамики изменения способности справляться с заданиями;

− возможность учета при построении расчетных оценок времени, затрачиваемого на выполнение заданий;

− меньшее по сравнению с другими подходами число заданий, которое следует предъявлять, что ускоряет процесс тестирования;

− развитая техника идентификации параметров моделей.

Указанные возможности обеспечивают преимущества нового подхода перед аналогами. Он наиболее эффективен не при начальном знакомстве с учебным материалом, а в ситуациях, когда требуется привести в систему и упорядочить уже полученные знания, умения и навыки: в частности, при подготовке к экзаменам.

В определенной степени на рассмотренную концепцию повлияли результаты, представленные в работе [Куравский, 2009], где концепция тренажера опирается на возможности нейронных сетей.

2. Концепция адаптивного тренажера

Выбор заданий в процессе тренажа проводится с помощью параметрических математических моделей, описывающихся марковскими случайными процессами с дискретными состояниями и непрерывным временем.

Модели для описания динамики переходов между состояниями с непрерывным временем представляются ориентированными графами, в которых вершины соответствуют состояниям, а дуги соответствуют переходам, для которых выполняются свойства пуассоновских потоков событий. Можно показать, что в этих потоках число событий X, попадающих в любой временной интервал длины τ, начинающийся в момент t, распределено согласно закону Пуассона:

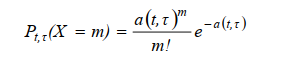
где 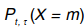– вероятность появления m событий в течение рассматриваемого интервала, 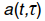– среднее число событий, 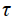попадающих в интервал длины 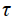, начинающийся в момент времени t. Рассматриваются только стационарные потоки, в которых 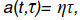, а 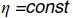есть интенсивность стационарного потока. Упомянутые выше предположения о свойствах потоков событий обычны для прикладных задач, так как эти потоки (или потоки, близкие к ним по свойствам) часто встречаются на практике благодаря предельным теоремам для потоков событий.

Для интерпретации результатов тренажа используются марковские процессы с дискретными состояниями, для которых заданы начальные распределения вероятностей и наблюдаемые частоты пребывания в состояниях 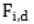в моменты времени 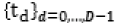, где i – индексы состояний рассматриваемого марковского процесса; D – количество моментов времени, в которые фиксировались частоты 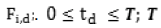– конечный момент времени. Интенсивности переходов между состояниями являются неизвестными (свободными) параметрами. Динамика изменения вероятностей пребывания в состояниях этих процессов определяется системой уравнений Колмогорова в матричной форме:

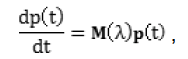
где 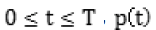представляет вероятности пребывания в состояниях процесса, λ – множество интенсивностей переходов между состояниями, М – матрица интенсивностей переходов между состояниями. Марковские процессы с непрерывным временем и свободными параметрами, идентифицируемые по данным наблюдений, далее называются сетями Маркова.

Для описания того, как вероятности нахождения в заданных состояниях изменяются со временем, применяются сети Маркова, организованные по схеме, которая представлена на рис. 1. Эта схема представляет собой конечную цепь из 2n+2 состояний, в которой переходы из состояния 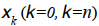возможны только в следующее по порядку состояние x_k+1 или состояние x_k*. Из состояний x₀ и x_n доступны только состояния x₁, x_0* и x_n* соответственно. Из состояния x_k* (k=0,…,n) доступно только состояние x_k . Для сетей указанного типа , матрица М имеет порядок 2n+2 .

Содержательному уровню знаний, умений и навыков, имеющему номер k, ставятся в соответствие состояния x_k и x_k*. Для каждого номера k определяется свое множество заданий соответствующего содержания. Чем правее состояние, тем шире допустимый набор знаний, умений и навыков. Состояниям с большим номером могут (но не обязаны) соответствовать задания, включающие знания, умения и навыки для состояний с меньшим номером. В общем случае, полный набор знаний, умений и навыков соответствует крайнему правому состоянию.

Под учащимся далее понимается человек, проходящий процедуру тренажа. Полагается, что каждый учащийся имеет один из заданных уровней подготовки 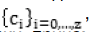, где (z+1) – число уровней подготовки, причем каждому из указанных уровней подготовки (например, высокому, среднему или низкому) ставятся в соответствие задания с определенным уровнем трудности. Каждому содержательному уровню знаний, умений и навыков соответствуют задания всех уровней трудности.

В случае пребывания учащегося в состоянии x_k, предъявляемое ему задание выбирается из множества, сопоставленного этому состоянию, случайным образом. Для каждого задания задается наибольшее допустимое время, отводимое для его выполнения.

Перемещения между состояниями определяются следующими правилами: 

– если учащийся, находясь в состоянии x_k, правильно выполняет полученное задание, не превысив заданных ограничений по времени, он переходит в состояние x_k+1;

– если учащийся, находясь в состоянии x_k, неправильно выполняет полученное задание, не превысив заданных ограничений по времени, он остается в состоянии x_k ;

– если учащийся, находясь в состоянии x_k и выполняя полученное задание, превышает заданные ограничения по времени, он переходит в состояние x_k*;

– если учащийся, находясь в состоянии x_k и выполняя полученное задание, превышает заданные ограничения по времени или неправильно выполняет полученное задание, не превысив заданных ограничений по времени, он остается в состоянии x_k;

– если учащийся, находясь в состоянии x_k*, правильно выполняет полученное задание, не превысив заданных ограничений по времени, он возвращается в состояние x_k .

В начальный момент времени учащийся находится в состоянии x₀. По завершении процедуры тренажа он оказывается в одном из состояний, наилучшим образом соответствующих его уровню знаний, умений и навыков. Тренаж завершается либо при превышении общего лимита времени, отведенного на эту процедуру, либо после успешного выполнения задания в состоянии x_n без превышения лимита времени, отведенного на это задание.

Значения свободных параметров марковских сетей идентифицируются путем сравнения наблюдаемых и прогнозируемых гистограмм, описывающих распределения частот пребывания в состояниях модели, а именно: вычисляются значения, обеспечивающие наилучшее соответствие наблюдаемых и ожидаемых частот попадания в определенное состояние системы в заданные моменты времени. При этом определяется набор интенсивностей λ, обеспечивающий наименьшее значение статистики Пирсона

Доказано, что, при выполнении ряда общих условий, значения указанной статистики x² (λ) ,получаемые при подстановке истинных решений, асимптотически описываются распределением x² с (2n+1)D– l степенями свободы, где l – число идентифицируемых параметров, причем вычисленные значения свободных параметров при увеличении объема выборки сходятся по вероятности к искомому решению. Это позволяет использовать статистику Пирсона для проверки гипотезы о том, что полученный прогноз согласуется с результатами наблюдений.

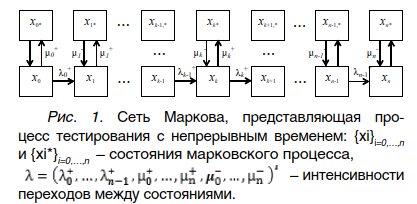
Идентификация марковских моделей с непрерывным временем проводится по выборкам учащихся, отдельно для каждого из рассматриваемых уровней подготовки. Каждому уровню подготовки с_i (i=0,…,z) при этом ставится в соответствие свой уникальный набор оценок параметров модели λ, что позволяет в дальнейшем выявлять значение этого показателя, наилучшим образом согласующегося с наблюдениями.

Для выполнения соответствующей процедуры необходимо задать систему уравнений 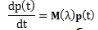, начальные условия p(0), начальное приближение λ^o,, наблюдаемые частоты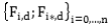пребывания в состояниях модели, шаг интегрирования  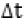 для численного решения системы уравнений и точность оценки. Для решения задачи идентификации авторами разработан специальный численный метод [Kuravsky, 2015]. В результате решения определяется вектор λ, доставляющий минимум функционалу x² (λ).

Зная состояние модели, в котором оказался тестируемый после решения последнего предложенного ему задания в определенный момент времени, и рассчитав с помощью дифференциальных зависимостей, заданных уравнениями Колмогорова, вероятность нахождения в этом состоянии в указанный момент времени для каждого из рассматриваемых уровней подготовки, можно оценить вероятности различных уровней подготовки при условии пребывания в указанном состоянии по формулам Байеса:

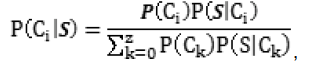
где C₁ – событие, связанное с наличием у тестируемого i-го уровня подготовки (i=0,…,z), s – событие, связанное с нахождением в заданном состоянии модели в указанный момент времени при указанном уровне трудности заданий, P(C₁) – априорная вероятность появления i-го уровня подготовки у тестируемого, 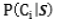– вероятность нахождения в заданном состоянии эталонной модели в указанный момент времени при наличии i-го уровня подготовки, – вероятность i-го уровня подготовки при условии нахождения в заданном состоянии модели в указанный момент времени.

Уровень подготовки, при котором достигается наибольшая условная вероятность,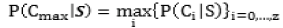 дает искомую оценку. Распределение вероятностей, 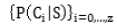, которое является результатом выполнения предъявленной последовательности заданий, позволяет оценить степень надежности полученного решения.

Сети Маркова, структура которых представлена на рис. 1, идентифицируются отдельно для каждого сочетания уровня подготовки и уровня трудности. Поскольку между уровнями подготовки и уровнями трудности здесь полагается взаимно-однозначное соответствие, для z+1 уровня подготовки требуется (z+1) ² идентифицированных сетей.

Трудность задания, предъявляемого учащемуся, соответствует текущей оценке его уровня подготовки. В начальный момент тренажа предъявляется задание с самым низким уровнем трудности и самым низким содержательным уровнем. После того как учащийся, находящийся в некотором состоянии сети Маркова, завершает попытку выполнения очередного задания, вычисляются z+1 указанных выше байесовских оценок вероятностей принадлежности его к рассматриваемым уровням подготовки. При этом используются только те идентифицированные сети Маркова, которые соответствуют уровню трудности последнего предъявленного задания. Если наиболее вероятным оказывается уровень подготовки, не совпадающий с оценкой, сделанной после выполнения предыдущего задания, то учащемуся приписывается этот вновь вычисленный наиболее вероятный уровень подготовки, а сам он переводится в начальное состояние x0 (происходит «сброс состояния»). Для переходов в это начальное состояние целесообразно обеспечить некоторую «инертность», выполняя их только в том случае, если указанная наибольшая вероятность превысит оценку вероятности текущего уровня подготовки не менее чем на заданное пороговое значение. По завершении попыток выполнения заданий самого низкого содержательного уровня «сбросы состояний» не происходят.

Таким образом, процесс тренажа сводится к предъявлению его участникам заданий, требующих для своего решения определенных знаний, умений и навыков при наличии определенного уровня подготовки. Формальная цель тренажа – привести обучающегося в крайнее правое состояние сети Маркова, что соответствует освоению всех знаний, умений и навыков при некотором уровне подготовки. В процессе тренажа используется адаптивный принцип выбора предъявляемых заданий, согласно которому их трудность должна соответствовать текущей оценке уровня подготовки учащихся. Согласно проведенным наблюдениям и результатам современной теории тестирования, такой подход обеспечивает наилучшую дифференциацию учащихся по степени их подготовки.

Задания предъявляются вместе с сопутствующими им комментариями и объяснениями. На первом этапе реализации эти комментарии и объяснения могут быть в виде текстов с рисунками и формулами, которые в последующем можно заменить видеофрагментами.

Как сети Маркова, так и указанные адаптивные переходы остаются скрытыми для учащихся, которые имеют доступ только к предъявляемым им заданиям и не знают всей сопутствующей математической подоплеки.

3. Программная реализация

Программная реализация адаптивного тренажера, выполненная А.С. Панфиловой, представлена в виде информационной интернет-системы, которая предназначена для изучения школьного курса математики. Эта система позволяет настраивать тренировочные материалы, а именно:

– вводить информацию о новых разделах и содержательных уровнях, представляющих собой темы, упорядочиваемые по степени сложности;

– создавать справочные материалы по темам с описанием различных способов решения тренировочных задач, аналогичных представленным;

– вводить задания с выбором различных алгоритмов проверки корректности ответа и указанием их трудности и допустимого времени, отведенного на решение.

В пилотной версии адаптивного тренажера (рис. 2) используются содержательные уровни, определяемые разделом дисциплины, и три уровня подготовки:

– умение выполнять действия по заданному образцу (низкий уровень),

– умение выполнять мыслительные операции, включая сравнение и анализ (средний уровень),

– умение творчески формировать новые способы решения задач из имеющихся правил и предписаний (высокий уровень).

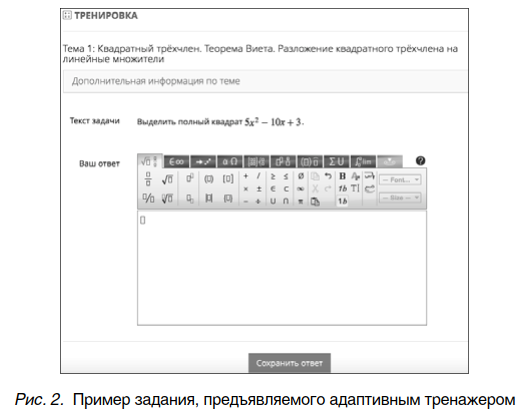
Более высокий содержательный уровень, как правило, требует знаний, умений и навыков, соответствующих предшествующим уровням (т. е. – в указанном смысле – с повышением содержательного уровня происходит накопление знаний, умений и навыков). Каждому сочетанию содержательного уровня и уровня подготовки соответствует свой набор задач, как показано в табл. 1. Количество задач в каждом наборе должно быть достаточным для проведения нескольких сеансов тренажа для одного учащегося.

Таблица 1. Распределение заданий по содержательным уровням и уровням подготовки

Уровень подготовки	Содержательный уровень 0	Содержательный уровень 1	…	Содержательный уровень n
Низкий уровень подготовки (0)	Набор заданий 0.0	Набор заданий 0.1	...	Набор заданий 0.n
Средний уровень подготовки (1)	Набор заданий 1.0	Набор заданий 1.1	…	Набор заданий 1.n
Высокий уровень подготов- ки (2)	Набор заданий 2.0	Набор заданий 2.1	…	Набор заданий 2.n

Программная реализация обеспечивает учет заданий, предъявленных каждому зарегистрированному учащемуся, так чтобы задания, получаемые как во время одного сеанса тренажа, так и во время разных сеансов, не повторялись.

Тренаж начинается с получения задания из набора 0.0. Далее, полагая, что учащийся находится в текущем состоянии x_k , он, согласно представленным выше правилам, получает задания в следующем порядке:

– если учащийся вовремя справляется с очередным заданием и байесовская оценка подтверждает его принадлежность выбранному в данный момент уровню подготовки, то он сдвигается вправо вдоль строки из табл. 1 и получает задание из следующего по порядку набора;

– если учащийся неправильно выполнил задание и байесовская оценка подтверждает его принадлежность выбранному в данный момент уровню подготовки, то он получает задание из того же набора, откуда было взято предыдущее (в протоколе выполнения заданий для этого учащегося делается пометка о неправильном выполнении задания, что в данном случае соответствует продолжению пребывания в состоянии x_k );

– если учащийся превысил лимит времени, отведенного для выполнения очередного задания, и байесовская оценка подтверждает его принадлежность выбранному в данный момент уровню подготовки, то он получает задание из того же набора, откуда было взято предыдущее (в протоколе выполнения заданий для этого учащегося делается пометка о превышении лимита времени, что в данном случае соответствует переходу в состояние x_k* );

– если байесовская оценка не подтверждает принадлежность учащегося выбранному в данный момент уровню подготовки и содержательный уровень предъявленного задания не является самым низким, то происходит «сброс состояния»: учащийся получает очередное задание из набора табл. 1, находящегося на пересечении столбца, соответствующего уровню 0, и строки, соответствующей наиболее вероятному уровню подготовки.

Полагая, что учащийся находится в текущем состоянии x_k* , он, согласно представленным выше правилам, получает задания в следующем порядке:

– если учащийся вовремя справляется с очередным заданием и байесовская оценка подтверждает его принадлежность выбранному в данный момент уровню подготовки, он получает задание из того же набора, откуда было взято предыдущее (в данном случае это соответствует переходу в состояние x_k );

– если учащийся неправильно выполнил задание и байесовская оценка подтверждает его принадлежность выбранному в данный момент уровню подготовки, то он получает задание из того же набора, откуда было взято предыдущее (в протоколе выполнения заданий для этого учащегося делается пометка о неправильном выполнении задания, что в данном случае соответствует дальнейшему пребыванию в состоянии x_k*);

– если учащийся превысил лимит времени, отведенного для выполнения очередного задания, и байесовская оценка подтверждает его принадлежность выбранному в данный момент уровню подготовки, то он получает задание из того же набора, откуда было взято предыдущее (в протоколе выполнения заданий для этого учащегося делается пометка о превышении лимита времени, что в данном случае соответствует дальнейшему пребыванию в состоянии x_k*);

– если байесовская оценка не подтверждает принадлежность учащегося выбранному в данный момент уровню подготовки и содержательный уровень предъявленного задания не является самым низким, то происходит «сброс состояния»: учащийся получает очередное задание из набора табл. 1, находящегося на пересечении столбца, соответствующего уровню 0, и строки, соответствующей наиболее вероятному уровню подготовки.

По завершении попыток выполнения заданий, соответствующих высокому уровню подготовки, учитывая их творческий характер, «сбросы состояний» не выполняются.

Для обеспечения разумной «инертности» переходов, «сброс состояния» выполняется только в том случае, если наибольшая вероятность превысит оценку вероятности текущего уровня подготовки не менее чем на заданное пороговое значение, которое полагается равным 0,05.

Тренаж завершается либо при превышении заданного общего лимита времени, либо после успешного выполнения задания из любой строки последнего столбца табл. 1 без превышения лимита времени, отведенного на это задание.

При идентификации параметров сетей Маркова «сбросов состояния» не происходит: вся процедура тренажа в контрольных группах учащихся проходит на заданиях, соответствующих одному и тому же уровню трудности. Поскольку уровень трудности не меняется, то байесовские оценки при идентификации не вычисляются. Всего требуется идентифицировать 9 эталонных сетей Маркова: каждая сеть определяется сочетанием одного из трех заданных уровней подготовки учащихся и трех соответствующих им уровней трудности заданий. В рассматриваемом случае, когда допускается высокий, средний или низкий уровень подготовки, необходимо автономно идентифицировать:

– сети, представляющие процесс выполнения заданий учащимися с высоким уровнем подготовки для заданий низкого, среднего и высокого уровня трудности;

– сети, представляющие процесс выполнения заданий учащимися со средним уровнем подготовки для заданий низкого, среднего и высокого уровня трудности;

– сети, представляющие процесс выполнения заданий учащимися с низким уровнем подготовки для заданий низкого, среднего и высокого уровня трудности.

При получении очередного задания учащемуся сообщаются темы, определяющие содержательный уровень этого задания.

Для отображения формул, записи ответов учащихся и хранения корректных ответов выбран синтаксис LaTeX и библиотека MathJax, интерпретирующая этот синтаксис и позволяющая сформировать представление уравнений в браузере пользователя. Учащемуся предлагается непосредственно вводить решение в соответствующее поле, поскольку такой формат ответа позволяет избежать угадывания и решения проблемы подбора дистракторов. На рис. 3 представлен редактор формул, позволяющий использовать различные математические символы при записи решения.

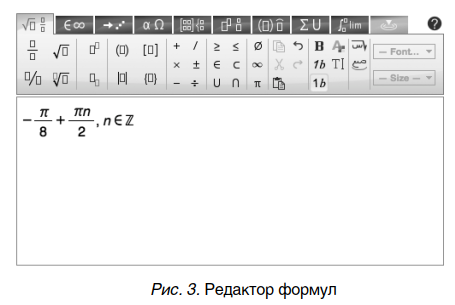
Автоматическая проверка корректности ответов реализуется с использованием API сервиса WolframAlpha [Wolfram Alpha Webservice], поддерживающего синтаксис LaTeX. Для проверки ответов на задания различного типа разработан ряд модулей, использующих методы системы WolframAlpha, и ряд алгоритмов сверки ответов. Разработан функционал, позволяющий администратору проверить корректность интерпретации системой различных вариантов ответов на задания.

Администратору системы доступна информация о результатах тренировок и причинах их завершения в виде графиков, диаграмм и таблиц, а также подробные сведения о каждом тренаже, решениях задач и показателях, на основании которых система принимает решение о параметрах следующего задания.

При реализации системы использовались языки PHP и JavaScript, СУБД MySQL, а также современные технологии, позволившие сделать работу с тренажером комфортной для всех категорий пользователей, а именно:

– адаптивный дизай н (Twitter Bootstrap);

– редактор формул для ввода ответа (Wiris Editor);

– преобразование формул в тексте заданий и справочных материалах (MathJax);

– построение графиков и диаграмм (EasyPieChart);

– экспорт накопленных данных и используемых справочников в формате электронной таблицы Excel;

– асинхронная передача данных (AJAX).

Для пилотной оценки эффективности применения адаптивного тренажера был проведен эксперимент, в котором участвовали две равноценные по составу выборки учащихся ГБОУ города Москвы «Гимназия 1540». Обе выборки включали по 10 человек с различной успеваемостью (от низкой до высокой), причем для каждого представителя одной выборки в другой выборке имелся аналог с теми же самыми учебными результатами. Учащиеся первой выборки, используя адаптивный тренажер, решали задачи по теме «Квадратные уравнения и неравенства». Учащиеся второй выборки с тренажером не работали. По окончании тренировки всем участникам эксперимента была предложена одна и та же контрольная работа по указанной теме, результаты которой оценивались по 100-балльной шкале. Эксперимент показал высокую эффективность адаптивного тренажера (рис. 4): средняя оценка результатов выполнения контрольной работы возросла в 2,85 раза, а стандартное отклонение оценок уменьшилось в 2,4 раза. Поскольку различие в средних значениях высокозначимо по t-критерию Крамера-Уэлча (p<0,00001)¹ , а различие в дисперсиях значимо по F-критерию (p<0,05), то выявленные эффекты могут рассматриваться как статистически достоверные.

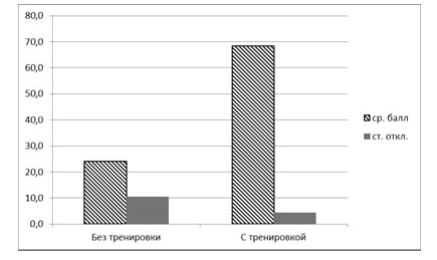
Рис. 4. Средние оценки и стандартные отклонения результатов выполнения контрольной работы для выборок учащихся, использовавших и не использовавших для своей подготовки адаптивный тренажер (результаты работы оценивались по 100-балльной шкале)

4. Основные результаты

1. Разработана концепция адаптивного тренажера, обеспечивающего выбор заданий с помощью параметрических математических моделей, описывающихся марковскими случайными процессами с дискретными состояниями и непрерывным временем.

2. Значения свободных параметров марковских процессов, применяемых для описания работы тренажера, идентифицируются с использованием наблюдаемых и прогнозируемых гистограмм, описывающих распределения частот пребывания в состояниях модели. Идентификация проводится отдельно для каждого из рассматриваемых уровней подготовки.

3. Принадлежность к различным уровням подготовки определяется с помощью байесовских оценок.

4. Программная реализация адаптивного тренажера выполнена в виде информационной интернет-системы с автоматической проверкой корректности ответов с использованием API сервиса WolframAlpha.

5. Особенностями диагностических методов, используемых при выборе предъявляемых заданий, являются: выявление и использование при построении расчетных оценок временной динамики изменения способности справляться с заданиями; возможность учета при построении расчетных оценок времени, затрачиваемого на выполнение заданий; меньшее по сравнению с другими подходами число заданий, которое следует предъявлять, что обеспечивает представленному подходу преимущества перед аналогами.

6. Пилотный эксперимент выявил, что использование адаптивного тренажера привело к статистически значимому улучшению результатов решения математических задач для контрольной выборки учащихся.

 

 

1. В русскоязычной литературе пока нет устоявшего термина для этой технологии тестирования. Существуют и другие варианты ее названия: стохастическая теория тестов, математическая теория измерений, теория ответов на вопросы, теория латентных черт, теория характеристических кривых заданий и т. д.

Финансирование:  работа выполнена при поддержке Российского фонда фундаментальных исследований (проект № 14-06-00191).

1. 1С: Электронное обучение [Электронный ресурс] // URL: http://v8.1c.ru/elo (дата обращения 06.02.2016).
2. Куравский Л.С., Кулик С.Д., Мармалюк П.А., Юрьев Г.А. Патент на полезную модель №118095, Российская Федерация (RU), кл. МПК G 09 B 23/02. «Устройство для моделирования адаптивного тестирования когнитивных способностей испытуемого». / Л.С. Куравский, С.Д. Кулик, П.А. Мармалюк, Г.А. Юрьев (Россия). Заявка № 2012105993/08, 21.02.2012; Зарегистр. 10.07.2012; Опубликовано 10.07.2012 Бюл. № 19; Приоритет от 21.02.2012 (РОСПАТЕНТ).
3. Куравский Л.С., Марголис А.А., Мармалюк П.А., Юрьев Г.А., Думин П.Н. Обучаемые марковские модели в задачах оптимизации порядка предъявления психологических тестов// Нейрокомпьютеры: разработка и применение. 2013. № 4. С. 28–38.
4. Куравский Л.С., Марголис А.А., Мармалюк П.А., Юрьев Г.А., Думин П.Н., Кулик С.Д. Патент на полезную модель №122796, Российская Федерация (RU) кл. МПК G09B 31/07. «Система поддержки принятия решений для психологического и педагогического тестирования». / Л.С. Куравский, А.А. Марголис, П.А. Мармалюк, Г.А. Юрьев, П.Н. Думин, С.Д. Кулик (Россия). Заявка №2012132684/08, 31.07.2012; Опубликовано 10.12.2012, Бюл. №34; Приоритет от 31.07.2012 (РОСПАТЕНТ).
5. Куравский Л.С., Марголис А.А., Юрьев Г.А. Психологический тренинг на основе нейросетевой технологии// Нейрокомпьютеры: разработка и применение. 2009. № 9. С. 20-26.
6. Куравский Л.С., Юрьев Г.А. Использование марковских моделей при обработке результатов тестирования// Вопросы психологии. 2011. № 2. С. 98-107.
7. Baker F.B. The Basics of Item Response Theory // ERIC Clearinghouse on Assessment and Evaluation, University of Maryland, College Park, MD. 2001.
8. Ebmodo [Электронный ресурс] // Connect with students and parents in your paperless classroom. URL: https://www.edmodo.com (дата обращения 03.02.2016).
9. Kats, Y. Learning Management Systems and Instructional Design: Best Practices in Online Education. IGI Global. 2013. ISBN 9781466639317
10. Kuravsky L.S., Marmalyuk P.A., Yuryev G. A. and Dumin P.N. A Numerical Technique for the Identification of Discrete-State Continuous-Time Markov Models // Applied Mathematical Sciences. Vol. 9. 2015. №8. 379–391 с. URL: https://doi.org/10.12988/ams.2015.410882.
11. Kuravsky L.S., Marmalyuk P.A., Yuryev G.A., Dumin P.N. and Panfilova A.S. Probabilistic Modeling of a Testing Procedure// Applied Mathematical Sciences. Vol. 9. 2015. №82. 4053–4066 с. URL: https://doi.org/10.12988/ams.2015.53234
12. Moodle open-source learning platform [Электронный ресурс] // Moodle Pty Ltd. URL:https://moodle.org (дата обращения 03.02.2016).
13. Rasch G. Probabilistic models for some intelligence and attainment tests// Copenhagen, Danish Institute for Educational Research, expanded edition (1980) with foreword and afterword by B.D. Wright. Chicago: The University of Chicago Press. 1960/1980.
14. Wolfram Alpha Webservice API [Электронный ресурс] // Wolfram Alpha LLC - A Wolfram Research Company. URL: http://products.wolframalpha.com/api/documentation.html (дата обращения 21.01.2016).
15. Wright B.D., Masters G.N. Rating scale analysis. Rasch measurements// Chicago: MESA Press. 1982. С. 206

PlumX

Метрики публикации