Работа посвящена численному анализу качества диффузионной аппроксимации управляемой одноканальной системы массового обслуживания в загруженном состоянии. Управление системой задается вероятностью отказа и интенсивностью обработки. Цель исследования - нахождение условий применимости диффузионной аппроксимации к модели управляемого марковского процесса, описывающего состояние системы. Качество аппроксимации характеризуется величиной равномерной метрики, определяющей расстояние между стационарными распределениями в исходной и приближенной модели, а также числовыми показателями, такими как средняя загрузка, среднее время ожидания, доля отклоненных заявок и объем затраченных ресурсов. Аппроксимация оказывается тем точнее, чем с большей вероятностью диффузионный процесс попадает в интервал доступа, т.е. интервал, в котором вероятность отказа меняется от нуля до единицы..
1. ВВЕДЕНИЕ
Современные системы передачи и обработки информации по своей сути являются системами массового обслуживания (СМО), в которых входной поток состоит из однотипных пакетов — небольших порций данных, предусмотренных сетевым протоколом [1,2]. Традиционные методы анализа и оптимизации СМО основаны на использовании марковских процессов с конечным множеством состояний [3,4].
Однако при значительном объеме трафика практическое применение данной методологии становится затруднительным из-за большого числа уравнений, описывающих стационарные вероятности состояний соответствующей СМО. Один из эффективных способов решения проблемы большой размерности, возникающей при оптимизации дискретных марковских процессов, является метод диффузионной аппроксимации [5,6].
Аналогично [7-9] в данной работе рассматривается одноканальная СМО, имеющая конечную очередь, принимающая на вход простейший поток и предусматривающая возможность управления характеристиками доступа и загрузки: вероятность отказа и интенсивность обработки. Однако в отличие от указанных работ далее система будет изучаться в условиях сильной загрузки. Кроме того, управление осуществляется за счет выбора параметров двух линейных функций, определяющих зависимость вероятности отказа и интенсивности обработки от числа заявок в системе. Обе функции отражают естественное требование роста числа отброшенных пакетов и скорости обработки при увеличении загрузки системы. Целью работы является нахождение условий применимости диффузионной аппроксимации к модели управляемого марковского процесса, описывающего число заявок в системе. В работе предлагается диффузионная аппроксимация, основанная на модели стохастического дифференциального уравнения с линейными сносом и диффузией [Alfonsi, 2015]. Устанавливается, что в зависимости от соотношения параметров системы стационарное распределение аппроксимирующего процесса является трехпараметрическим гамма-распределением или гауссовским.
Если назвать интервалом доступа тот промежуток, в котором вероятность отказа как функция состояния меняется в интервале (0,1). Тогда основной результат работы можно сформулировать следующим образом: качество аппроксимации зависит от вероятности попадания диффузионного процесса в интервал доступа. Поэтому если вероятность отказа априори отделена снизу от нуля и сверху от единицы, то диффузионная аппроксимация вполне приемлема для приближенного описания и последующей оптимизации управляемой СМО с интенсивным входным потоком.
2. ОПИСАНИЕ МОДЕЛИ


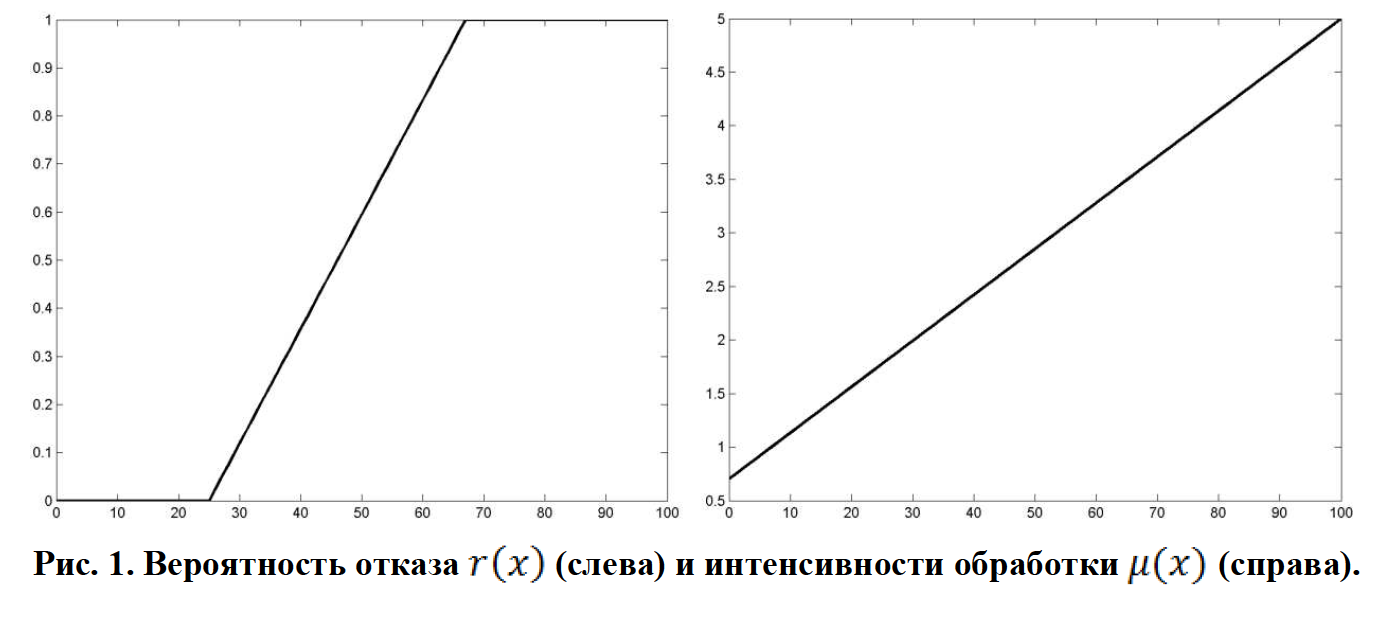
3. МЕТОД ДИФФУЗИОННОЙ АППРОКСИМАЦИИ



4. ХАРАКТЕРИСТИКИ ДИФФУЗИОННОГО ПРОЦЕССА
5. РЕЗУЛЬТАТЫ ЧИСЛЕННОГО ЭКСПЕРИМЕНТА

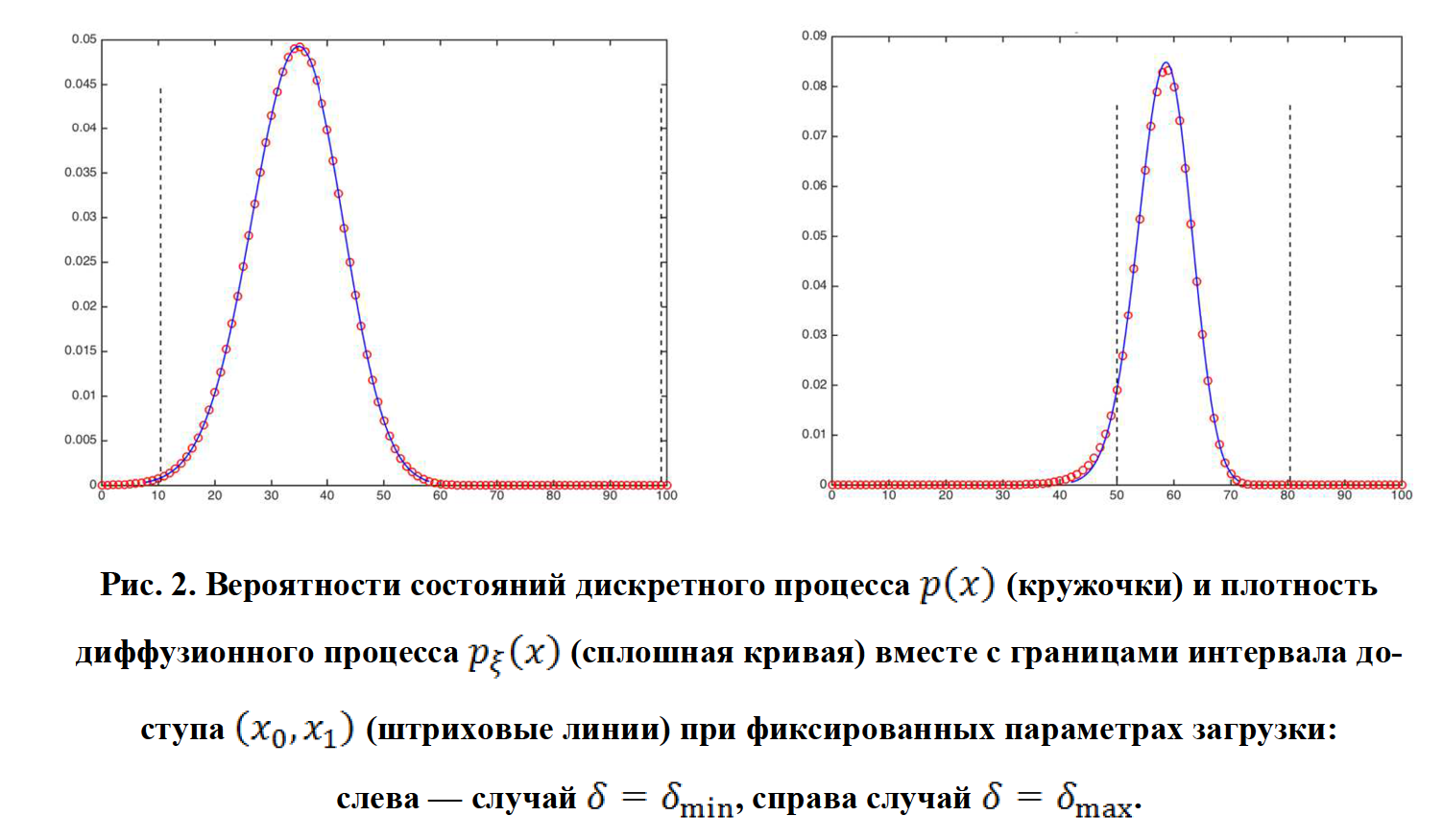
Дальнейшие результаты сравнения при различном объеме очереди N приведены в следующей таблице.
|
|
$тах |
L |
Lf |
W |
W, |
R |
Rf |
M |
|
|
50 |
0.0852 |
28.5406 |
29.0533 |
29.3120 |
26.4121 |
0.3510 |
0.2667 |
1.1 |
1.1 |
|
100 |
0.0485 |
57.9109 |
58.1067 |
50.1537 |
44.5091 |
0.3495 |
0.2667 |
1.1 |
1.1 |
|
500 |
0.0189 |
290.532 |
290.533 |
250.423 |
222.545 |
0.3483 |
0.2667 |
1.1 |
1.1 |
|
1000 |
0.0134 |
581.0667 |
581.0667 |
500.730 |
445.0909 |
0.3482 |
0.2667 |
1.1 |
1.1 |
|
2000 |
0.0094 |
1162.13 |
1162.13 |
1001.34 |
890.1818 |
0.3481 |
0.2667 |
1.1 |
1.1 |
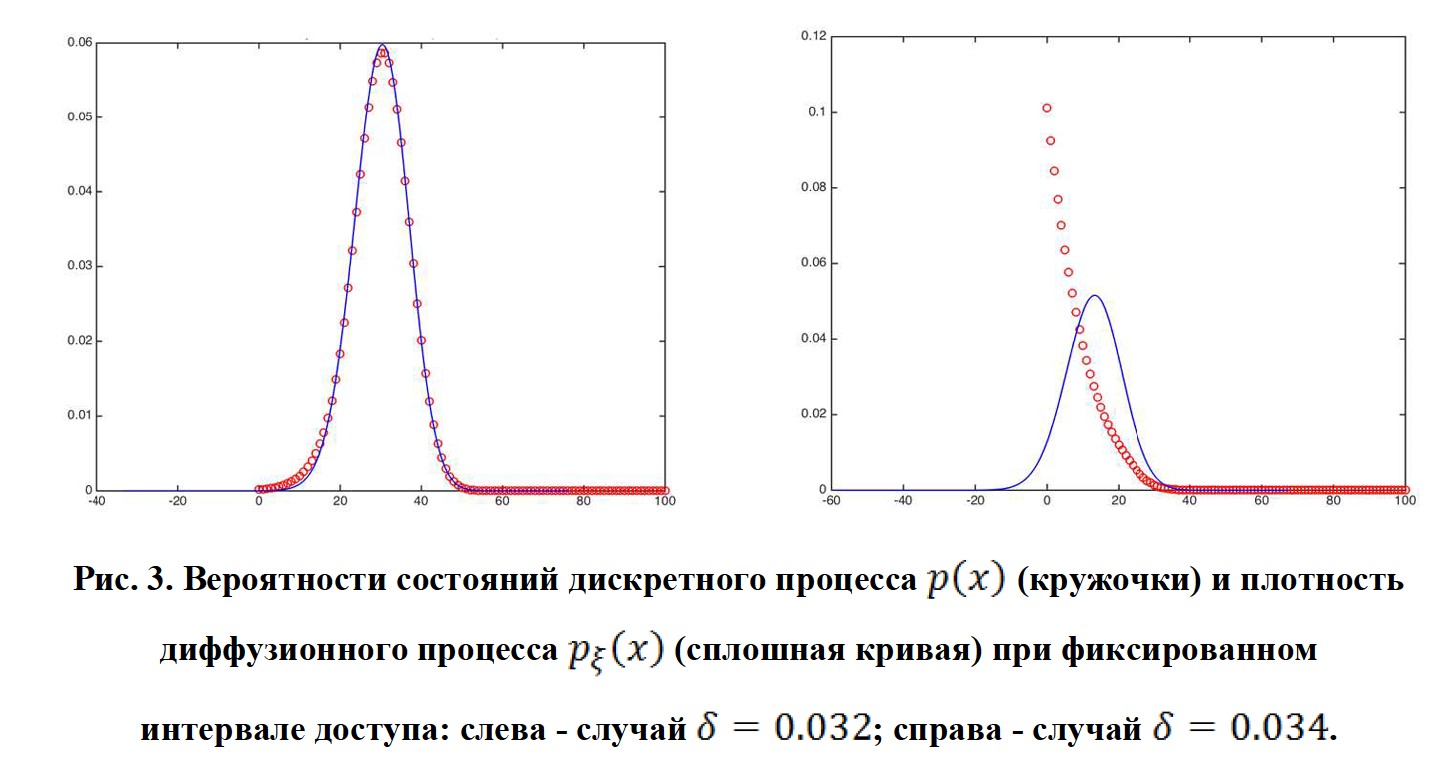

6. ЗАКЛЮЧЕНИЕ
В работе рассмотрена модель одноканальной системы массового обслуживания с управляемыми доступом и загрузкой. Вероятность отклонения и интенсивность обслуживания предполагались линейно зависящими от состояния системы. Предложена диффузионная аппроксимация на базе стохастического дифференциального уравнения с линейными коэффициентами сноса и диффузии. Для трех показателей работы системы (среднее время пребывания, доля отказов, средний объем ресурсов) определена зависимость от управляющих параметров. Численный анализ показал, что качество диффузионной аппроксимации стационарного распределения дискретного марковского процесса зависит от вероятности попадания диффузионного процесса в интервал доступа. Если эта вероятность близка к единице (это характерно для ситуации сильной загрузки), то модель диффузионного процесса можно использовать для приближенного описания управляемой одноканальной системы массового обслуживания.

