Моделирование и анализ данных
2019. Том 9. № 3. С. 4–10
ISSN: 2219-3758 / 2311-9454 (online)
О моделировании свободных движений спутника вокруг Земли
Аннотация
Общая информация
Ключевые слова: Движение спутника, метод малого параметра, аналитические приближения
Рубрика издания: Моделирование
Тип материала: научная статья
Для цитаты: Кондратьева Л.А. О моделировании свободных движений спутника вокруг Земли // Моделирование и анализ данных. 2019. Том 9. № 3. С. 4–10.
Полный текст
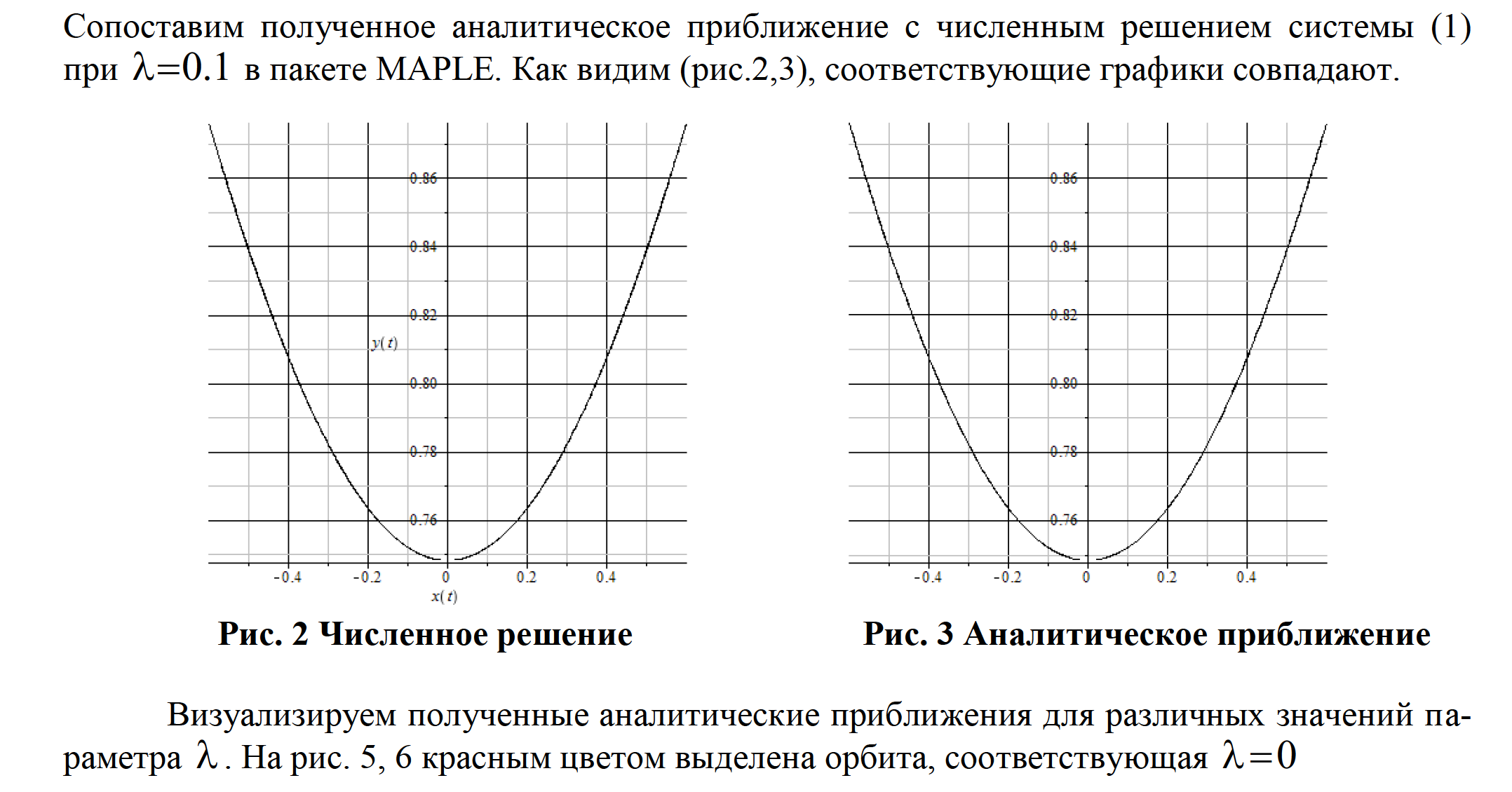
В рамках известной модели Дилиберто-Кайнера-Фройнда ставится задача аналитического определения эволюции свободных орбит спутников при движении вокруг Земли. На основе метода малого параметра предложен алгоритм для отыскания их приближенного представления. Полученные аналитические формулы определяют положение спутника как функции долготы. Приведены результаты аналитических расчетов, которые хорошо согласуются с численными решениями.
ВВЕДЕНИЕ
Анализ движения спутников небесных тел остаётся одной из приоритетных задач нелинейной динамики. Наиболее существенное возмущение орбит спутников Земли связано с отклонением земного поля тяготения от центрального. Как известно, Земля представляет собой «сплюснутый у полюсов шар», у которого полярный радиус на 21 км короче экваториального.
Постоянная, ответственная за сжатие планеты, - один из основных параметров, связанных с запуском искусственных спутников Земли и отслеживании их движения на картах Земной поверхности. Сейчас разработаны новые методы наблюдения ИСЗ, которые позволяют определить положение спутника с точностью ± 2 см. Возникло новое направление небесной механики, позволяющее по движению спутника определять возмущающие силы - гравитационное поле планеты. Обратные задачи динамики успешно используются для решения задач - как геофизики, так и астрофизики.
Напомним, как влияет отклонение земного поля тяготения от сферического на орбиты спутников.
Наиболее сильно оно сказывается на положении плоскости орбиты. Эта плоскость не остается неизменной, а непрерывно поворачивается в пространстве. Если провести перпендикуляр к этой плоскости из центра Земли, то он будет описывать конус вокруг оси симметрии Земли, напоминающий конус, который описывает при вращении ось волчка.
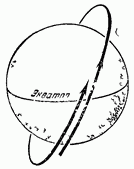
Рис. 1 Смещение орбиты за один виток
Поворачивание плоскости орбиты именуется её прецессией. В результате прецессии, спутник, совершив один оборот, пересекает экватор западнее, чем раньше, даже если предположить, что Земля не вращается (рис.1).
Плоскость полярной орбиты, из соображений симметрии, неподвижна; для круговых орбит, близких к экваториальной, это смещение происходит быстрее всего. Для низких орбит оно составляет 0,6° по экватору за один виток. При этом за один виток спутник смещается на 33,5 км в направлении, перпендикулярном к плоскости орбиты. Возмущение от не сферичности Земли падает по мере увеличения радиуса круговой орбиты.
1. ПОСТАНОВКА ЗАДАЧИ
Мы рассматриваем модель свободного движения спутника Земли, описанную в работе [2] и воспроизведённую в монографии [3]. Нашей целью является задача приближённого аналитического определения эволюции орбит спутника на основе метода малого параметра Пуанкаре и асимптотического метода Крылова-Боголюбова, а также сравнение аналитических расчетов с численными решениями.
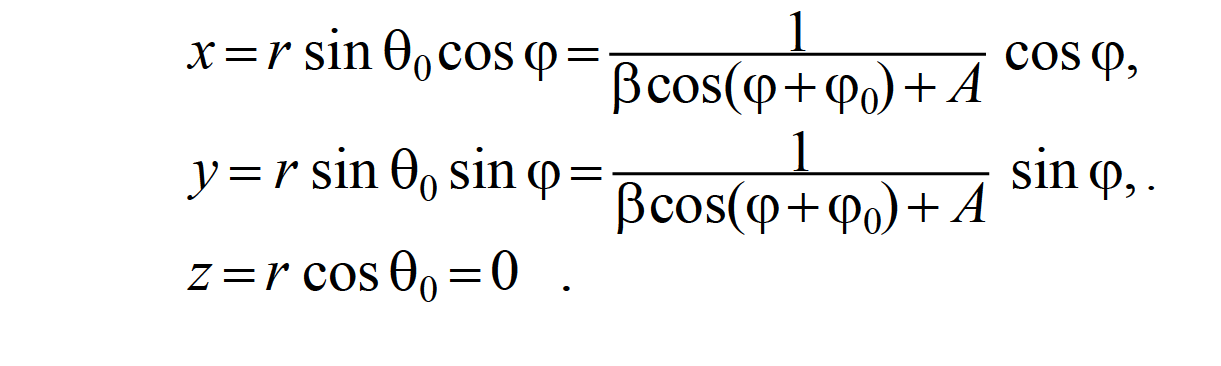
2. МЕТОДЫ МАЛОГО ПАРАМЕТРА И КРЫЛОВА-БОГОЛЮБОВА
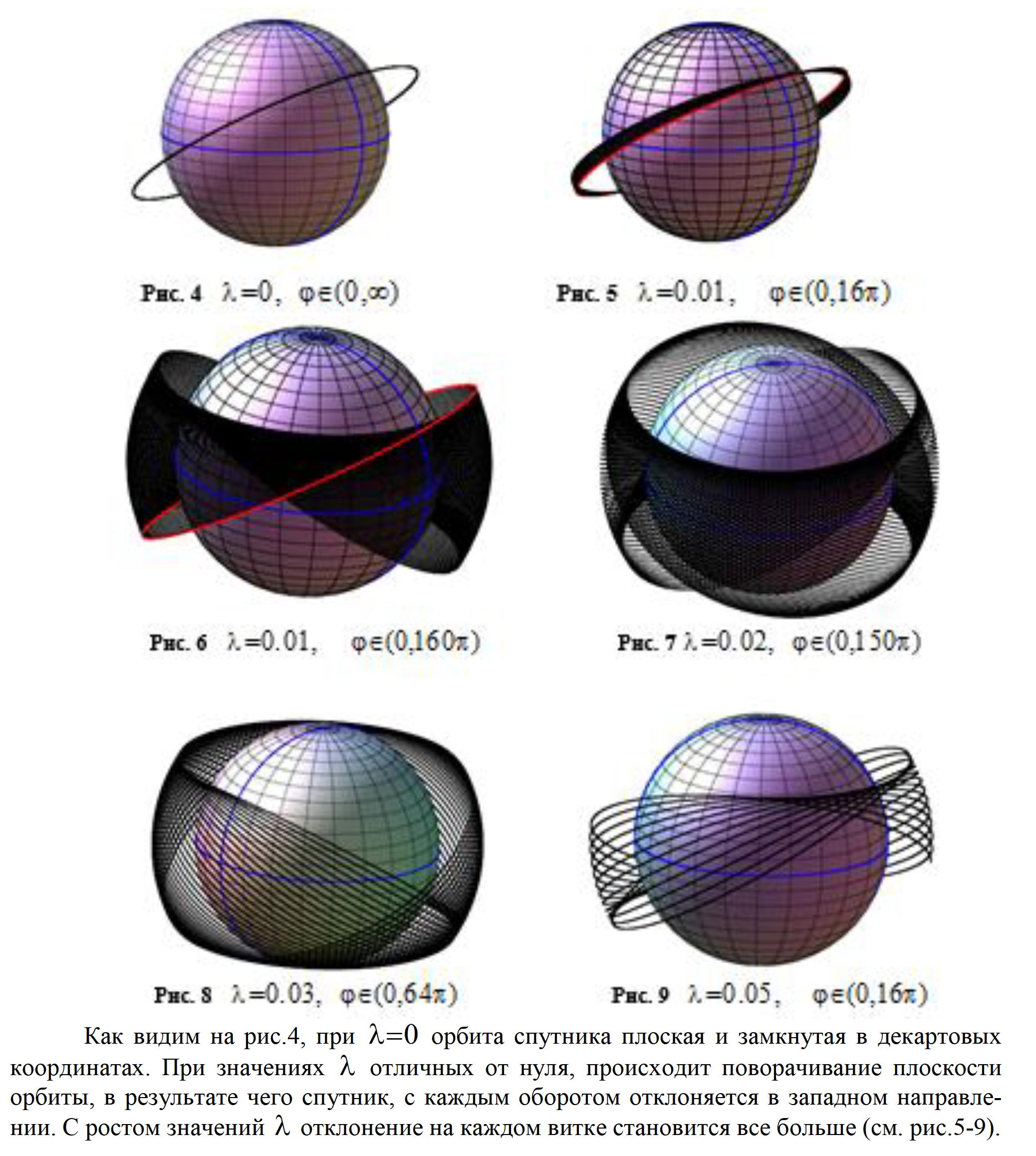
3. АНАЛИЗ ПОЛУЧЕННЫХ РЕЗУЛЬТАТОВ
Литература
-
Боголюбов Н.Н., Митропольский Ю.А. Асимптотические методы в теории нелинейных колебаний. М.: Наука, 1974, 503 с.
-
Diliberto S.P., Kayner W.T., Freund R.J. The application of periodic surface theory to the study of satellite orbits // Astronom. J. 1961. V. 66, № 3, P. 118–128.
-
Митропольский Ю.А., Лыкова О.Б. Интегральные многообразия в нелинейной механике. М.: Наука, 1973, 512 с.
Информация об авторах
Метрики
Просмотров
Всего: 434
В прошлом месяце: 5
В текущем месяце: 1
Скачиваний
Всего: 240
В прошлом месяце: 2
В текущем месяце: 2