Моделирование длительности жизни выдающихся ученых математиков, родившихся в 20 веке в СССР и в странах мира

Выполнено математическое моделирование и проведена сравнительная оценка долголетия, рожденных в 20-м столетии известных ученых-математиков СССР и стран мира, активная жизнь которых длилась в период существования СССР. Для моделирования сформирована выборка статистических данных, на основании которой построены таблицы частот и функция распределения вероятности смерти ученых-математиков, рожденных и работавших в СССР и в странах мира. Моделирование осуществлено с помощью полиномиальных функций инструментом «Регрессия» ППП Excel. Осуществлен сравнение функций распределения вероятности смерти известных ученых-математиков СССР и ученых-математиков, проживавших в разных странах мира в период существования СССР.

Введение

Как известно в геронтологии смерть человека, а соответственно и продолжительность жизни человека, определяется предельной временной точкой процесса старения. Вместе с тем, как показали исследования, на продолжительность жизни человека оказывает влияние кроме генетических факторов также место проживания в горной местности или на равнине, уровень доходов, доступность медицинской помощи, образование, профессия, социально-экономический статус, творческий характер жизни, достигнутый интеллект и др. [1]. Влияние ряда из названных факторов освещены в работах [1-6].

Многолетние научные исследования показывают, что причина долгой жизни обусловлена условиями и образом жизни. Она составляет три четвертых всех процентов и только одна четвертая оставшиеся часть процентов заложены в генах. Полагают, что если человеку будут обеспечены оптимальные жизненные условия, влияющие на долголетие, то он будет иметь возможность максимально увеличить продолжительность жизни в отведенных ему биологией пределах [7]. Очевидно, что годы войн нарушают нормальные жизненные условия и ускоряют старения, а соответственно снижают длительности жизни человека.

Цель настоящей работы направлена на изучение влияния различных факторов на процесс старения у творческих людей Советского Союза, живших в условиях войн и проживших более шестидесяти лет. Исследованию подвергались ученые, которые сформировались и достигли выдающихся научных успехов в области математики. Одновременно сравнивалась продолжительность их жизни с длительностью прожития выдающихся ученых-математиков других стран, которые проживали в период существования СССР.

Как известно опыт последних столетий наглядно показывает, сколь велико значение математики в мировом развитии. Одновременно известно, что для математиков характерен свой особый режим труда, не связанный с временем суток. Дополнительно исследованиями установлено, что высокий интеллект, свойственный выдающимся ученым-математикам, способствует большей продолжительности жизни и долголетию [8, 9].

Родившиеся в начале 20-го века многие выдающиеся математики СССР с первых дней войны принимали участие в защите страны: призывались в армию, записывались в народное ополчение, шли на фронт добровольцами. Нелегкая доля досталась многим из них. Все, чья жизнь была сохранена, как в гражданскую, так в Великую Отечественную войну, продолжили учебу и совершенствовали свои знания, добиваясь в смертельных условиях новых научных результатов мирового уровня. Достижения ученых-математиков в области военной техники являются значимой частью победы в войне.

Необходимо отметить, что в период Великой Отечественной войны техника требовала совершенных математических расчетов. Прежде всего это необходимо было для увеличения скорости полета самолетов не только за счет повышения мощности двигателей, но и выбора оптимального профиля фюзеляжа и крыльев. Решения многих математических вопросов позволило достичь блестящих результатов в совершенствовании боевых самолетов: А. С. Яковлеву и С.А. Лавочкину создать грозные истребители, С. В. Илюшину – неуязвимые штурмовики, А.Н. Туполеву и Н. Н. Поликарпову – мощные бомбардировщики.

Выдающийся советский математик М. В. Келдыш и возглавляемый им коллектив ученых исследовали опасные явления, возникающих при маневрах самолетов, что позволило советской авиационной науке своевременно защитить конструкции скоростных самолетов от появления опасных вибраций.

А. Н. Крылову, чьи труды легли в основу математической теории непотопляемости и качки кораблей, позволившие использовать в нашем Военно-морском флоте корабли с  высокой живучестью.

Теория функции действительного переменного и аксиоматика теории вероятностей академика С. Н. Бернштейна позволила рассчитать таблицы для определения местонахождения судна по радиопеленгам, что дало возможность ускорять штурманские расчеты во много раз.

Член – корреспондент АН СССР Н. Г. Четаев в результате решения сложной математической задачи определил оптимальною крутизну нарезки стволов орудия, что позволило обеспечивать максимальную кучность боя.

Один из крупнейших наших математиков, академик А.Н. Колмогоров, используя свои работы по теории вероятности, разработал теорию минимального рассеивания артиллерийских снарядов.

Приведенные примеры можно продолжить, однако для этого потребуется осветить дела всех выдающихся ученых-математиков СССР, которые представлены в табл. 1 в качестве выборки для проведения исследования. Следует отметить, что выборка построена по данным «Библиографического словаря» [10], которые дополнялись данными о смерти тех ученых в выборке, чья жизнь завершалась после издания словаря.

Таблица 1.  Выборка ученых-математиков СССР, проживших более 60-и лет

К сожалению, имена многих ученых математиков не вошли в данную выборку, так как их жизнь завершилась в годы войны или ранее 60 лет. Страна помнит и ежегодно отдает должное своему народу, которые отдали свою жизнь во имя независимости, свободы и общественных идеалов. В их числе и воины, которые в мирное довоенное время сформировались как ученые математики.

Необходимо отметить огромный вклад, который внесли в создание и развитие математической науки ученые многих других стран. В табл. 2 для сравнения приведена выборка выдающихся ученых-математиков, которые родились и развивали математическую науку во многих странах в период существования СССР. Для формирования выборки использованы статистических данных ученых-математиков, представленные в [11].

Таблица 2. Выборка ученых-математиков народов мира, проживших более 60-и лет

На основании численного состава каждой выборки выдающихся ученых-математиков построена таблица частот смертности. В таблице смертности указаны количество умерших из общего числа ученых, представленных в выборках, за интервал прожития в один год. 

Таблица 3. Таблица смертности ученых, согласно выборок табл. 1 (СССР) и табл. 2 (МИР)

Эта таблица рассматривается как модель процесса вымирания ученых, которые содержатся в рассматриваемых выборках выдающихся математиков. Из таблицы смертности получены коэффициенты смертности, которые представляют дискретные значения относительного количества (частости) смертей или приближенные значения вероятности смерти в заданный год прожития. Под вероятностью смерти понимается вероятность события, что если ученый вступил в определенный возрастной интервал лет, то он доживет только до его верхней границы. На основании значений коэффициентов смертности получены дискретные математические законы —  функции распределения вероятностей. В дальнейшем дискретные законы преобразованы в непрерывные законы распределения.

Таким образом, для более качественного проведения сравнения длительности жизни ученых вместо дискретного времени использованы непрерывное время смерти, а вместо функции распределения вероятности дискретной случайной величины функция распределения вероятности непрерывной случайной величины.

Принятая непрерывная функция распределения позволяет определить вероятности того, что ученый доживёт до некоторого заданного возраста х лет, где х – действительное непрерывное число, характеризующее возраст прожития [12].

В качестве моделей длительности активной жизни ученых математиков в работе построены непрерывные полиномиальные функции распределения вероятности прожития. Область задания в работе ограничена принятым в работе интервалом значений лет прожития, а именно от шестидесяти до ста лет.

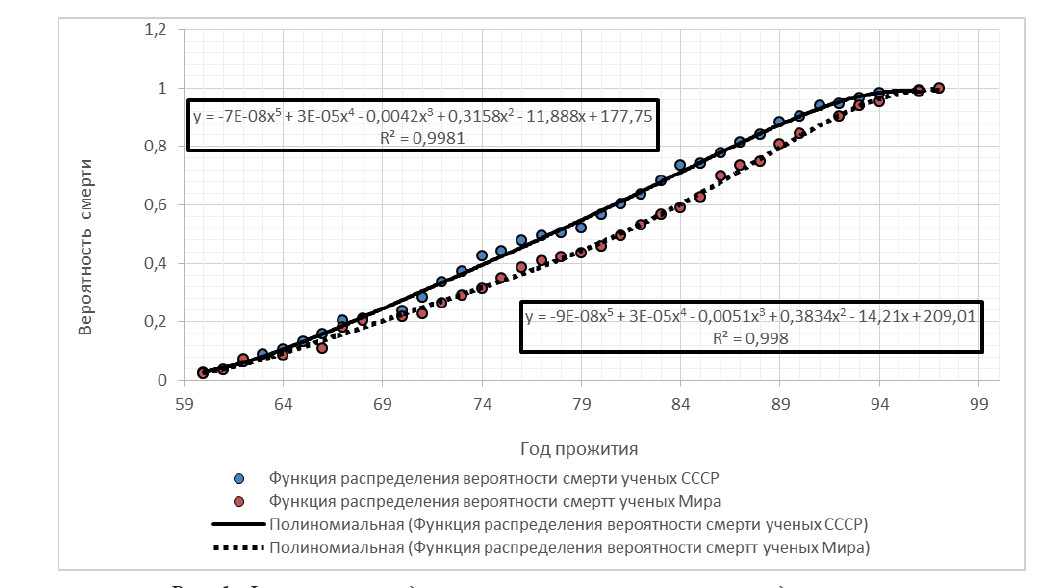
Графики непрерывных функций распределения вероятности смерти ученых математиков, представляющие собой кривые распределения вероятности прожития, ее выражение и коэффициент детерминации, представлен на рис. 1. Функция построена по данным табл.3.  с помощью метода наименьших квадратов.

Рис. 1. Функция распределения вероятности смерти от года прожития

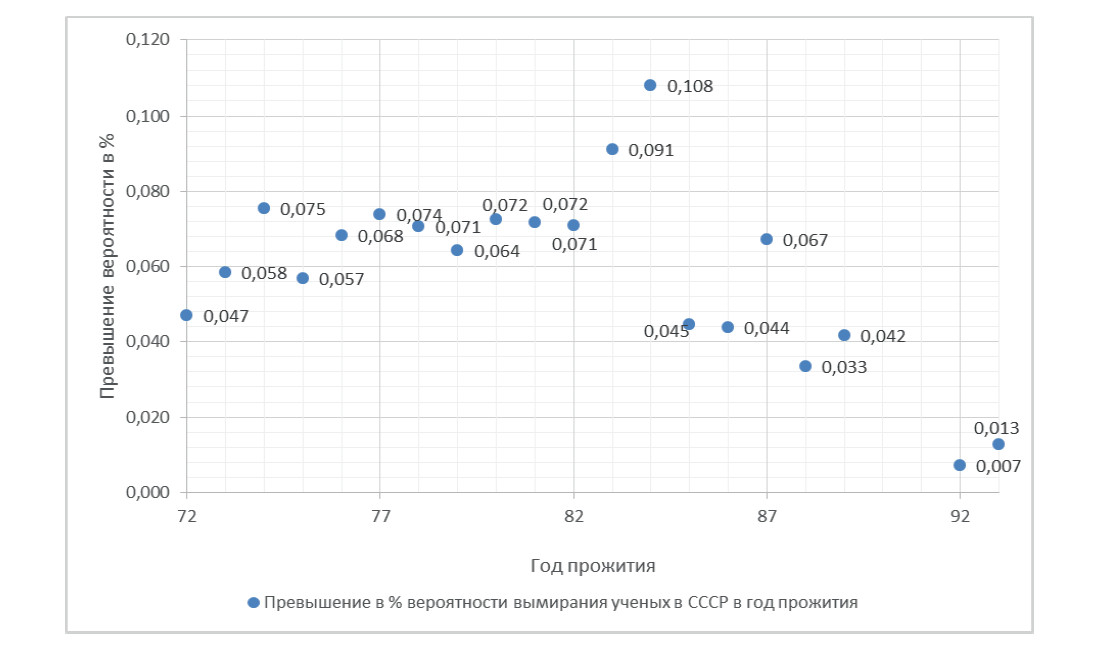
Используя законы распределения вероятности смерти вычислена разность между вероятностями длительности жизни двух коллективов (выборок) ученых, из которых математики СССР проживали в значительно более сложных условиях по сравнению с математиками других стран мира. На рис. 2 представлены превышения вероятностей смерти в процентах.  Из представленных значений на рис. 2 следует, что вероятность смерти в рассматриваемой год прожития от семидесяти до девяноста трех лет у коллектива выдающихся ученых-математиков СССР несколько выше.

Рис. 2. Превышение вероятности смерти ученых-математиков СССР над учеными других стран в %

Наибольшее превышение вероятности смерти возникает в районе 84 лет и составляет до 0,1%. Такое незначительное расхождение можно предположительно объяснить созданием в СССР, даже в тяжелые военные и в послевоенные годы, приемлемых условий для творческой активной жизни выдающихся ученых математиков. Другими словами, условия жизни и работы в военные и послевоенные годы оказали незначительное снижение длительности жизни выдающих ученых-математиков СССР. Что касается влияния самой интеллектуальной деятельности на срок жизни ученых СССР и ученых стран мира, то можно полагать, что она была равнозначной.  

1. Гаврилов Н.А. Гаврилова Н.С. Биология продолжительности жизни / Отв. ред. В.П. Скулачев — 2-е изд., перераб. и доп. М.: Наука, 1991 — 280 с.
2. Анисимов В.Н. Молекулярные и физиологические механизмы старения: [в 2 т.] / 2-е изд., перераб. и доп. СПб: Наука, 2008. Т. 1. — 481 с.; Т.2. — 434 с.
3. Анисимов В.Н. Синдром ускоренного старения при воздействии канцерогенных факторов окружающей среды // Рос. физиол. журн. 2010. Т. 96. № 8. С. 817–833.
4. Пучкова Е.И., Алишев Н.В. Показатели биологического возраста и ускоренное старение у ликвидаторов последствий радиационных аварий // Усп. геронтол. 2011. Т. 24. №1. С. 99–104.
5. Анисимов В.Н., Михальский А.И. Стареет ли Нобелевский лауреат? Математический анализ возраста продолжительности жизни лауреатов Нобелевской премии за 1901–2003 гг. // Усп. геронтол. 2004. Т. 15. С. 14–22.
6. Берёзкин В.Г., Буляница А.Л. О некоторых демографических характеристиках членов Российской академии наук в ХХ в. // Усп. геронтол. 2007. Т. 20. № 1. С. 29–39.
7. Жаринов Г.М., Анисимов В.Н. Продолжительность жизни, долгожительство и некоторые причины смерти у литераторов разных жанров //Усп. геронтол. 2016. Т. 29. №2. С. 210–217.
8. Анисимов В.Н., Жаринов Г.М. Средний возраст смерти и долгожительство мужчин-ученых различных специальностей //Вестн. моск. ун-та. сер.16. Биология. 2016. № 4.12-18.
9. Правила долголетия. Результаты крупнейшего исследования долгожителей: http://belibra.ru/Pravila-dolgolyetiya-Ryezuljjtaty-krupnyeyishyego-isslyedovaniya-dolgozhityelyeyi.html (дата обращения: 12.10.2021).
10. Бородин А.И., Бугай А.С. Биографический словарь деятелей в области математики. / Пер. с укр. — К.: Радянська школа, 1979 — 680 с.
11. Collected Works in Mathematics and Statistics: https://www.mscs.dal.ca/~dilcher/collwks.html#top (дата обращения: 13.09.2021).
12. Герасименко П.В. Сравнительный анализ активной жизни выдающихся ученых-математиков, рожденных в разные столетия. // Известия Петербургского университета путей сообщения. – СПб.: ПГУПС, 2022. – Т. 19. – Вып. 1. – С. 105-115.