Введение
Объективная оценка эффективности работы пилотов важна для оценки рисков, связанных с информационно-управляющим полем (ИУП) кабины экипажа воздушного судна, оптимизации ИУП и обучения экипажей. Одной из критических проблем при этом является разработка критериев оценки. Данные, основанные на характеристиках действий экипажей, могут быть использованы для объективной оценки эффективности обучения и навыков, приобретенных в его результате. Таким образом, актуальна разработка методов компьютеризированной диагностики, которые можно применять в ходе подбора летного состава для оценки уровня полученных знаний, способностей и навыков. Эти методы помогут улучшить объективность, информативность и точность оценок, а также обеспечить стандартизацию и автоматизацию измерений. Особое значение имеют разработка и анализ новых подходов, которые могут применяться для оценки уровня обучения и психофизиологического состояния пилотов. При этом основным направлением является диагностика по результатам работы на современных тренажерах и стендах, где возможно воспроизведение особых условий работы пилотов.
Под риском понимается мера количества опасности, измеряемой в форме экспертного значения сочетания двух величин — нормированной частоты или меры возможности случайного появления опасных событий и возможного обобщенного ущерба от этих событий [ГОСТ Р ИСО/МЭК, 2011]. Классический подход к количественной оценке рисков пилотирования основывается на оценке вероятности ошибок экипажа, значение которой изменяется в зависимости от различных условий и обстоятельств.
Анализ концепций и технологий, используемых на сегодняшний день для снижения рисков и тяжести последствий авиационных инцидентов, показывает существенный интерес профессионального сообщества к различным аспектам проблемы безопасности полетов. С усложнением авиационной техники и ростом числа перелетов становится возможным формирование концепций предотвращения инцидентов, построенных на базе математических моделей с использованием детализированной информации как о параметрах пилотирования воздушных судов, так и о состоянии пилотов, диспетчеров и других членов экипажа.
Важно отметить, что подходы к оценке рисков, требующие использования многочисленных и трудно идентифицируемых параметров летательных аппаратов и их систем, не имеют перспектив практического применения, поскольку погрешности оценки указанных параметров, а также, как правило, неопределенная степень чувствительности результата оценки к варьированию этих параметров делают данные подходы предельно ненадежными. Вопросы структурной устойчивости моделей оценки рисков обычно даже не рассматриваются.
Большие проблемы на практике создают расчетные модели, требующие детализации оценки рисков по подсистемам летательного аппарата. Поскольку при решении задачи необходимо рассматривать большое количество взаимодействующих систем, это приводит к перебору многочисленных вариантов поведения сложной технической системы, что неприемлемо усложняет анализ.
Подходы, опирающиеся на статистический анализ больших выборок, включая данные о выходе из строя отдельных систем, позволяют выявлять тенденции, но не дают возможности делать определенный прогноз в конкретной практической ситуации, что существенно ограничивает возможности применения.
Кроме того, переход от одного типа летательного аппарата к другому требует для большинства рассмотренных подходов практически полной переделки всей расчетной модели.
К сожалению, практически все разработанные ранее методы имеют один и более из перечисленных недостатков.
Если исходить из критериев простоты практического применения, отсутствия привязки расчетной модели к конкретному типу летательного аппарата (универсальности) и отсутствия необходимости детально исследовать трудоемкие проблемы чувствительности и структурной устойчивости расчетных моделей, то модели оценки рисков пилотирования целесообразно строить на непосредственном анализе измеряемых параметров полета и интегральных оценках фрагментов полетов в целом, без детализации по параметрам (недостатки такой детализации рассмотрены в последующем разделе), а также данных видеооку- лографии, позволяющих надежно оценивать влияние ИУП кабины экипажа на эффективность пилотирования. Один из вариантов такого подхода рассмотрен в этой работе.
К настоящему времени получено определенное количество результатов, связанных с выявлением аномально выполненных летных упражнений [1; 2; 5; 7—13; 15—16; 31—33; 37; 39, 40]. В подавляющем большинстве случаев рассматриваются только параметры траектории воздушного судна. Существенные ограничения, ограничивающие применение указанных результатов на практике, рассмотрены в [28-30]. Следует отметить, что одним из основных недостатков является применение традиционных метрик для сравнения фрагментов полетов, поскольку эти метрики не обеспечили решение исследуемой и связанных с ней задач.
В связи с тем, что один из наиболее популярных, но наименее эффективных простых методов оценки качества пилотирования заключается в проверке того, находятся ли определенные параметры в заданных пределах критических значений для указанных режимов полета, неизбежны комментарии на эту тему. Валидность такого подхода лучше всего пояснить с помощью следующей аналогии: он выглядит, как попытка оценить качество вождения автомобиля количеством столкновений с забором вдоль дороги, игнорируя при этом всю остальную информацию о движении автомобиля. Очевидно, что эффективность и уместность таких оценок не выдерживает критики.
Существующие проблемы преодолеваются с помощью методов [28-30]. Далее представлены способы оценки навыков с использованием полученных экспериментально релевантных данных о пилотировании. В результате их применения определяются классы навыков с использованием параметров полетов, выявляемых в процессе выполнения упражнений. Под параметрами полетов далее понимаются измеряемые характеристики, определяющие движение и состояние систем летательного аппарата.
Чтобы анализировать данные о пилотировании, необходима специализированная база данных, в которой собраны паттерны их деятельности, характеризующие выполнение упражнений пилотами с различным уровнем подготовки. Под паттерном понимается представление определенного фрагмента анализируемой деятельности, называемого упражнением, с помощью набора релевантных параметров. Эти паттерны соотносятся с одним из распознаваемых уровней сформированности навыков.
Собранные в базе данные должны включать в себя параметры выполнения упражнений, а также соответствующие комментарии, содержащие экспертные оценки из различных источников, включая различные типы тренажеров и стендов, системы виртуальной реальности, а также результаты реальной работы. Комментарии экспертов должны выявлять слабые стороны работы экипажей, охватывая информацию о типичных ошибках в терминах параметров деятельности и советы инструктору о том, как исправить указанные недостатки.
Общее допущение для рассматриваемых подходов заключается в том, что действия, выполняемые разными стилями и с разным качеством, а также упражнения разных типов отделяются друг от друга в многомерном пространстве, сформированном в метриках вейв- лет-представлений различных вариантов работы экипажей или в метрике правдоподобия траекторий собственных значений для преобразований параметров деятельности. Это утверждение обосновывается результатами вычислительных экспериментов, использующих релевантные эмпирические данные. Общий метод, вытекающий из этого заключения, опирается на выбор паттернов.
Данные подходы могут быть использованы для поддержки процесса обучения пилотов, формирования инструкторских оценок, а также для обеспечения автоматической оценки качества пилотирования в режиме реального времени. Эти средства анализа существенно отличаются от вероятностных методов, применяемых при управлении системами, прогнозировании технических неисправностей, мониторинге состояния и поддержке управляющих действий пилотов [Красильщиков, 2011].
Оценка рисков человеческого фактора при пилотировании воздушного судна
Поскольку под риском понимается мера количества опасности, то модель рисков человеческого фактора при пилотировании воздушного судна (ВС) фактически представляет собой модель оценки рисков. Разработанная модель оценки рисков человеческого фактора, связанных с ИУП кабины экипажа воздушного судна, представлена на рис. 1. Эта модель построена на сравнениях представлений оцениваемых действий экипажей с сопоставимыми представлениями действий различных типов и качества исполнения, образующих репрезентативную выборку и содержащихся в заранее сформированной специализированной базе данных.
Риск представляется вероятностными оценками, которые строятся в результате последовательного применения метода главных компонентов, многомерного шкалирования и кластерного анализа к трем типам характеристик:
— параметрам полета и состояния систем воздушного судна;
— траекториям движения глаз;
— временным рядам первичных показателей глазодвигательной активности (ГДА), что приводит к формированию кластеров фрагментов полетов различных типов и качества исполнения, включая аномальные.
Обобщенный дискриминантный анализ обеспечивает вычисление вероятностного профиля принадлежности к целевым кластерам, на основе которого строится итоговое заключение.
Ключевым элементом используемого подхода являются три новые метрики, обеспечивающие значимую дискриминацию фрагментов полетов различных типов и качества исполнения, а именно: евклидова метрика и метрика Кохонена для вейвлет-представле- ний различных вариантов работы экипажей, а также метрика правдоподобия траекторий собственных значений для преобразований параметров деятельности, — без применения которых многомерное шкалирование и кластерный анализ не дали бы желаемый результат.
Выполняется детализация вкладов параметров полета и состояния систем воздушного судна в различия фрагментов полетов в заданной метрике, результаты которой используются при содержательном анализе причин выявляемой аномальности.
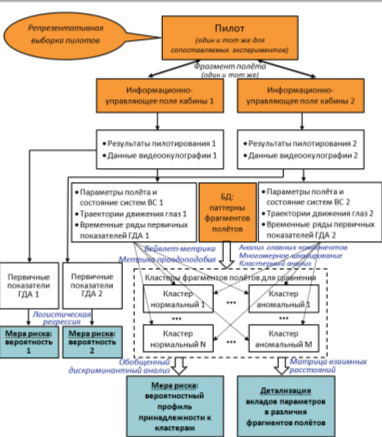
воздушного судна, при пилотировании воздушного судна
В качестве упрощенного альтернативного подхода, вероятность риска также может оцениваться по первичным показателям ГДА, используя логистическую регрессию.
Анализ параметров деятельности экипажа, представленных с помощью дискретных вейвлет-преобразований их временных рядов
Полагается, что работа экипажа представлена набором временных рядов, описывающих динамику параметров технической системы, а также, если возможно, состояние пилотов. Основные этапы рассматриваемого анализа и их взаимные связи приведены на рис. 2.
Можно выделить следующие цели данного анализа:
— обеспечение оценки результатов текущей деятельности путем ее сравнения с паттернами, предварительно собранными в соответствующей базе данных;
— распознавание аномальной деятельности и выявление параметров, характеризующих ошибки пилота, с целью определения источников аномальности.
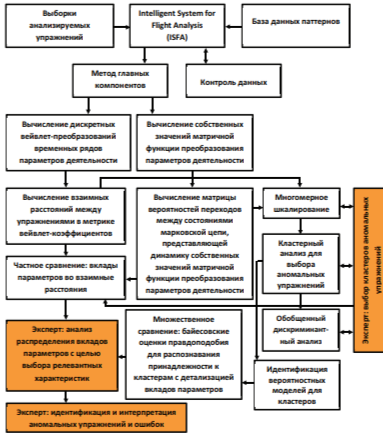
Рис. 2. Основные этапы анализа и связи между ними (действия экспертов выделены цветом)
На этапе предварительной обработки выбираются временные интервалы для сравнения упражнений и проводится нормализация данных.
Избыточная информация исключается с помощью метода главных компонентов [René Vidal, Yi, 2016; Xiangyu Kong, Changhua, 2017]. Для этого рассчитываются матрицы взаимных корреляций временных рядов, решается алгебраическая задача собственных значений и определяется, до какой степени можно уменьшить размерность собственного подпространства исследуемых параметров, так чтобы оно содержало достаточно представительную часть изменчивости наблюдаемых параметров. По каждому из выбранных собственных направлений этого подпространства (главному компоненту) по одной из самых высоких компонентных нагрузок выбирается представитель из числа регистрируемых параметров (переход в базис главных компонентов нецелесообразен из-за неопределенности содержательной интерпретации главных компонентов и — в ряде прикладных задач — из-за отсутствия точной синхронизации исследуемых процессов для различных упражнений во времени). Цель этого этапа — выявить относительно независимые характеристики, заменяющие группы существенно коррелирующих параметров лишь одним характерным представителем, чтобы избежать на последующих этапах искажений, обусловленных комбинированным воздействием сильно зависимых характеристик.
Временные ряды, характеризующие исследуемые процессы, заменяются на ряды вейвлет-коэффициентов, полученных в результате кратномасштабного анализа [Neal, 2010]. При этом исходные процессы как функции времени заменяются интегральными характеристиками временных интервалов, которые относятся к области определения этих функций, что позволяет обеспечить значительное сокращение (примерно на порядок величины) количества коэффициентов, необходимых для правильного представления анализируемых процессов. Благодаря правилам соотнесения вейвлет-коэффициентов с фрагментами временных рядов, которые применяются в кратномасштабном анализе, преодолеваются трудности, связанные с необходимостью точной синхронизации процессов, относящихся к различным упражнениям одного типа, поскольку наиболее значимые коэффициенты, относящиеся к более продолжительным временным интервалам, практически нечувствительны к умеренным сдвигам во времени.
Для исследуемых упражнений далее следует либо вычислить матрицу взаимных расстояний между вейвлет-представлениями различных вариантов работы экипажей в евклидовой метрике и метрике Кохонена, либо применить подход, при котором в метрике правдоподобия траекторий собственных значений рассчитываются аналогичные матрицы, связанные с наблюдаемыми фрагментами деятельности. Матрицы взаимных расстояний, вычисленные для всех рассматриваемых параметров, складываются, в результате чего получается общая матрица взаимных расстояний между исследуемыми упражнениями. При анализе аномально выполненных упражнений вычисляются относительные вклады параметров деятельности в элементы матриц взаимных расстояний, что позволяет определить параметры, характеризующие ошибки пилота, с целью выявления причин аномальности.
Для анализа взаимного расположения упражнений в пространстве приемлемой размерности, после расчета матрицы взаимных расстояний выполняется многомерное шкалирование [3,38]. Вычисленное распределение анализируемых упражнений в построенном пространстве многомерного шкалирования далее используется для определения расстояний между упражнениям при формировании диагностических выводов. Размерность пространства шкалирования определяется по критерию достаточной дифференциации выборок упражнений, относящихся к различным распознаваемым классам. Выполнение этого этапа обеспечивает последующее разделение в пространстве шкалирования упражнений различных типов и нормальных/аномальных результатов деятельности.
Для выявления кластеров, представляющих различные типы упражнений и классы навыков пилотов, в полученном пространстве шкалирования для паттернов выполняется кластерный анализ. Полученные результаты позволяют создать классификационные правила для разделения различных уровней качества выполнения упражнений, а также их типов в пространстве шкалирования; при этом различия между кластерами различных вариантов выполнения одних и тех же упражнений объясняются тем, что их реализация обусловлена индивидуальными навыками.
Для описания вероятностной динамики каждого класса навыков пилотов с целью прогнозирования его поведения, для каждого кластера паттернов, применяя процедуру идентификации, создаются вероятностные модели, представленные марковскими случайными процессами с дискретными состояниями и непрерывным временем [6; 19—26; 34].
Вычисление расстояний до центров кластеров паттернов или до ближайших паттернов основываются на результатах выполнения последовательности контрольных упражнений. Если объем выборок паттернов достаточно велик, расстояния определяются до центров кластеров паттернов, определённых, опираясь на полученные ранее данные многомерного шкалирования. Если выборки паттернов небольшие, то определяется ближайший паттерн, который можно найти двумя способами: или непосредственно путем вычисления паттерна, ближайшего в метрике вейвлет-представлений, или путем определения ближайшего паттерна в полученном пространстве шкалирования.
Доступны три способа определения класса навыков:
— прямое сравнение анализируемых упражнений с паттернами деятельности из базы данных в метрике вейвлет-представлений, связанной с наблюдаемыми упражнениями (этот способ рассматривается как основной), а также
— вероятностные оценки распознавания класса навыков с помощью обобщенного дискриминантного анализа, используя выборочные функции распределения расстояний упражнений до центров кластеров в пространстве шкалирования (этот способ рассматривается как вспомогательный), и
— байесовские оценки правдоподобия (выбор класса навыков с помощью вероятностного профиля пребывания в диапазонах параметров деятельности — этот способ также рассматривается как вспомогательный).
При этом эксперт отвечает за:
— выбор кластеров аномальных упражнений;
— анализ баланса вкладов параметров при сравнении упражнений с целью выбора релевантных параметров для дальнейшего исследования,
— выявление и интерпретацию аномалий и ошибок.
Необходимые вычисления обеспечивает Intelligent System for Flight Analysis (ISFA) [Куравский] — система, в которой разработанные методы реализованы в среде графического программирования LabVIEW [Bress Thomas, 2013].
Евклидова метрика вейвлет-представлений различных вариантов работы экипажей и метрика правдоподобия траекторий собственных значений для преобразований параметров деятельности детально рассмотрены в [28-30]. Описание метрики Кохонена, разработанной после публикации этих работ, представлено в следующем разделе.
Пример практического применения рассматриваемого подхода, демонстрирующий автоматическую оценку рисков пилотирования в режиме реального времени, представлен в Приложении.
Метрика Кохонена в пространстве вейвлет-коэффициентов
Расчет значений метрики Кохонена в пространстве вейвлет-коэффициентов выполняется с помощью самоорганизующихся карт признаков Кохонена (карт Кохонена) [Faure, 2017; Kohonen, 2001]. Каждому параметру действий экипажа требуется своя карта Кохонена. На входные слои этих структур подаются вейвлет-коэффициенты, представляющие параметры действий экипажей. Выходные слои (топологические карты) образуют прямоугольные матрицы, состоящие из элементов на радиальных базисных функциях (рис. 3). Для каждого элемента обучающей выборки определяется нейрон, ближайший к нему в евклидовой метрике («выигравший» нейрон). Затем, взяв взвешенную сумму прежнего центра «выигравшего» нейрона и соответствующего элемента обучающей выборки, параметры «выигравшего» нейрона и нейронов из его окрестности корректируются так, чтобы они в большей степени стали похожи на входной элемент, причем реализуемый «сдвиг» центров нейронов делается достаточно малым. В процессе обучения указанная окрестность сжимается до нуля. В результате последовательности таких коррекций определенные области топологической карты итерационно «сдвигаются» к определенным элементам обучающей выборки, при этом близкие входные данные обеспечивают «выигрыш» близко расположенных элементов топологических карт. Таким образом, самоорганизующиеся карты Кохонена учатся «понимать» структуру входных данных. Концепция этих карт построена на аналогии с ассоциативными свойствами человеческого мозга.
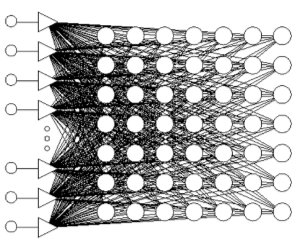
Рис. 3. Входной и выходной слои самоорганизующейся карты Кохонена
Взаимные расстояния между вейвлет-преобразованиями пар исследуемых процессов, представляющих различные действия экипажей, определяются как средние значения двух следующих разностей:
— между расстоянием карты Кохонена от представления первого процесса до его «выигравшего» нейрона и расстоянием карты Кохонена от представления второго процесса до вычисленного «выигрышного» нейрона первого процесса, и, наоборот,
— между расстоянием карты Кохонена от представления второго процесса до его «выигравшего» нейрона и расстоянием карты Кохонена от представления первого процесса до вычисленного «выигрышного» нейрона второго процесса.
Общее взаимное расстояние является суммой соответствующих расстояний для всех параметров действий экипажей. Поэтому, как и в случае евклидовой метрики в пространстве вейвлет-коэффициентов, могут быть вычислены оценки относительных вкладов параметров действий в элементы матриц взаимных расстояний.
Пример, иллюстрирующий эффективность использования трех рассматриваемых метрик при сравнении фрагментов полетов разных типов, обсуждается в следующем разделе.
Сравнение рассматриваемых метрик на примере прикладной задачи
Чтобы проиллюстрировать эффективность применения трех рассматриваемых метрик, ниже представлен анализ 34 летных упражнений пяти типов: «восстановление из сложного пространственного положения», «сдвиг ветра», «заход на посадку с одним двигателем», «отказ двигателя при взлете» и «полет по кругу», — выполненных на универсальном стенде прототипирования Государственного НИИ авиационных систем (ГосНИИАС) (рис. 4). Матрицы взаимных расстояний, вычисленные с помощью евклидовой метрики и метрики Кохонена в пространстве вейвлет-коэффициентов, показывают хорошо выраженные различия между упражнениями разных типов (рис. 5 a, c). Эта же матрица, вычисленная в метрике правдоподобия, также показывает эти различия, однако они не столь явно выражены (рис. 5 b).

Рис. 4. Универсальный стенд прототипирования кабины экипажа Государственного НИИ авиационных систем
Диаграммы рассеяния летных упражнений, полученные в результате многомерного шкалирования, представлены на рис. 6. Для количественной оценки качества дискриминации между рассматриваемыми типами упражнений может быть использована статистика Уилкса (L-статистика). Ее значения лежат в интервале от 0 до 1, причем близкие к нулю значения свидетельствуют о хорошей дискриминации, а близкие к единице — об ее отсутствии. Поскольку описание распределения статистики Уилкса, которое доступно в настоящее время, не является достаточно точным и полным, для оценки значимости дискриминации используется хорошо изученное F-отношение (называемое в данном контексте ассоциированной F-статистикой). Значения статистики Уилкса при этом пересчитываются в значения F-статистики, которая используется для проверки гипотезы о совпадении центроидов исследуемых типов упражнений.
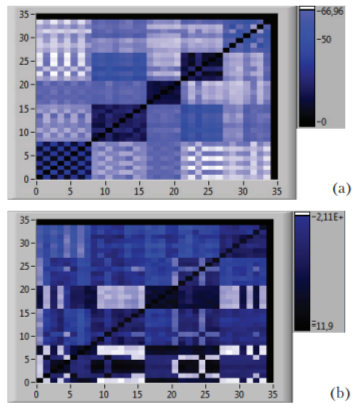
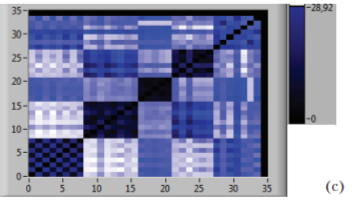
Рис. 5. Матрицы взаимных расстояний для 34 летных упражнений пяти типов, вычисленные с помощью: (a) евклидовой метрики в пространстве вейвлет-коэффициентов; (b) метрики правдоподобия; (c) метрики Кохонена в пространстве вейвлет-коэффициентов
Значения указанных статистик, показанные в табл. 1, подтверждают, что евклидова метрика и метрика Кохонена обеспечивают высокозначимую дискриминацию между упражнениями различных типов, в то время как метрика правдоподобия приводит к достаточно значимой дискриминации в целом. Линейный дискриминантный анализ Фишера показывает несколько меньшее количество неправильных решений в случае метрики Кохонена. В целом, несмотря на совершенно разные способы построения, евклидова метрика и метрика Кохонена в данной задаче дают примерно одинаковые результаты.
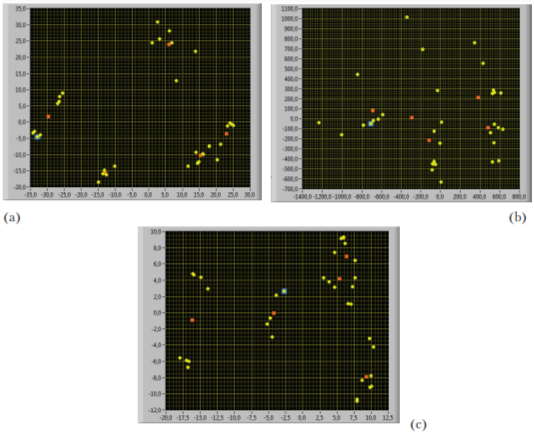
многомерного шкалирования в случае: (a) евклидовой метрики в пространстве
вейвлет-коэффициентов; (b) метрики правдоподобия; (c) метрики Кохонена в пространстве
вейвлет-коэффициентов
Таблица 1
евклидовой метрики, метрики правдоподобия и метрики Кохонена: статистика Уилкса и ассоциированная F-статистика
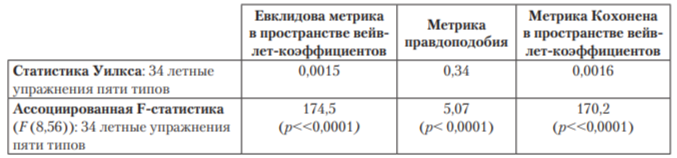
Учитывая существенно различную природу построенных метрик, разумно не выбирать одну или две из них, а использовать их одновременно, сопоставляя полученные результаты.
Упрощенный подход: оценка вероятности риска принятия неправильного решения по первичным показателям ГДА с помощью логистической регрессии
Оценка вероятности риска принятия неправильного решения однозначно (как дополнение до единицы) связана с вероятностью принятия правильного решения, приводящего к устранению критической ситуации. Оценка этого показателя выполняется в два этапа:
— идентифицируется зависимость этой вероятности от некоторого параметра, доступного для оценок по экспериментальным данным;
— проводятся измерения с целью оценок указанного параметра с помощью айтрекера.
В качестве такого параметра далее рассматривается продолжительность принятия решения.
Будем полагать, что R = tr0 + t, где R — продолжительность критической ситуации, tr0 — продолжительность считывания и обработки пилотом информации с индикаторов, t — продолжительность принятия решения.
Полагаем, что при достаточно большом времени для вероятности принять правильное решение адекватна модель Г. Раша [Kuravsky, 2015а], представленная логистической функцией (рис. 7):
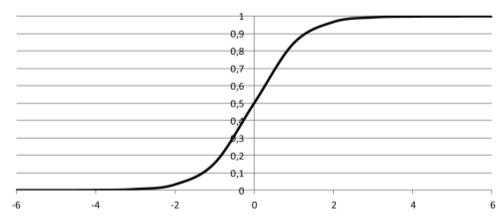
Рис. 7. Модель Г. Раша, представленная логистической функцией

где L — значение в шкале логитов, r — вероятность правильного выполнения задания. В случае оценки трудности этот параметр характеризует возможность выполнения определенного задания для всего множества субъектов, а в случае оценки способностей — результаты определенного субъекта для всего множества допустимых заданий. Статистические приближения указанных величин получаются после замены в приведенной формуле вероятности r на ее выборочные оценки.
Похожая логистическая функция (рис. 8) используется для представления зависимости способности принять правильное решение C(t) от продолжительности обдумывания решения t: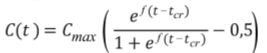
Величина tcr представляет индивидуальные особенности пилотов.
Далее полагаем, что величины t и tcr безразмерны и измеряются в логитах:

Матрицы правильности принятия решений имеют вид (единица представляет правильное решение, а 0 — неправильное).





Значения величины q можно перебирать в разумном диапазоне, выбирая уровень, при котором будет достигнуто приемлемое увеличение вероятности принятия правильного решения для заданных трудностей заданий (ситуаций).
Продолжительность считывания и обработки информации с индикаторов tr0 в первом приближении можно оценивать как сумму продолжительностей фиксаций взора в течение критической ситуации с верхней границей в 320 мс (т. е. фиксации, продолжительности которых превышают 320 мс, учитываются как фиксации с продолжительностью 320 мс). Как показывают эксперименты, индивидуальные особенности пилотов на данную характеристику влияют достаточно слабо.
Пример логистической регрессии для оценки риска по одному из первичных показателей ГДА приведен на рис. 9. Исследуемым показателем ГДА являлось время, потраченное на обдумывание ситуации, планирование действий и принятие решений, оцениваемое по продолжительности фиксаций взора в процессе считывания и интерпретации показаний индикаторов (когда взгляд направлен на приборы, а не на окно кабины). Параметры логистической регрессии идентифицировались методом максимального правдоподобия.
Основные результаты и выводы
1. Разработана модель рисков человеческого фактора при пилотировании воздушного судна. Эта модель построена на сравнениях представлений оцениваемых действий экипажей с сопоставимыми представлениями действий различных типов и качества исполнения, образующих репрезентативную выборку и содержащихся в заранее сформированной специализированной базе данных. Риск представляется вероятностными оценками, которые строятся в результате последовательного применения метода главных компонентов, многомерного шкалирования и кластерного анализа к трем типам характеристик: параметрам полета и состояния систем воздушного судна, траекториям движения глаз и временным рядам первичных показателей глазодвигательной активности, — что приводит к формированию кластеров фрагментов полетов различных типов и качества исполнения, включая аномальные. Дискриминантный анализ обеспечивает вычисление вероятностного профиля принадлежности к целевым кластерам, на основе которого строится итоговое заключение.
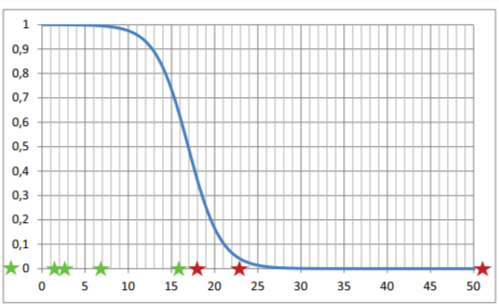
Рис. 9. Логистическая регрессия для оценки вероятности принятия правильного решения по продолжительности фиксаций взора в процессе считывания и интерпретации показаний индикаторов (зеленые звездочки соответствуют успешно выполненным упражнениям, а красные — неудачным попыткам; по оси абсцисс отложен исследуемый показатель)
2. Ключевым элементом представленного подхода являются три новые метрики, применяемые для сравнений действий экипажей и обеспечивающие значимую дискриминацию фрагментов полетов различных типов и качества исполнения, а именно: евклидова метрика и метрика Кохонена для вейвлет-представлений различных вариантов работы экипажей, а также метрика правдоподобия траекторий собственных значений для преобразований параметров деятельности, — без применения, которых многомерное шкалирование и кластерный анализ не дали бы желаемый результат. Учитывая различную природу трёх применяемых метрик, целесообразно использовать их параллельно, сопоставляя полученные результаты.
3. Выполняется детализация вкладов параметров полета и состояния систем воздушного судна в различия фрагментов полетов в заданной метрике, результаты которой используются при содержательном анализе причин выявляемой аномальности.
4. В качестве упрощенного альтернативного подхода, вероятность риска оценивается по первичным показателям глазодвигательной активности, используя логистическую регрессию.
5. Полученные результаты позволяют создать классификационные правила для разделения различных уровней качества выполнения упражнений, а также их типов в пространстве шкалирования, при этом различия между кластерами различных вариантов выполнения одних и тех же упражнений объясняются тем, что их реализация обусловлена индивидуальными навыками.
6. Оценка рисков пилотирования сводится к определению вероятностей принадлежности к целевым кластерам, связанным с типами упражнений и качеством пилотирования.
7. При достаточной скорости вычислений, рассмотренный анализ полетных данных в автоматическом режиме может быть выполнен в реальном времени.