Эрлангенская программа Клейна и геометрия треугольника

В данной статье сопоставляются геометрия треугольника и Эрлангенская программа Ф. Клейна, в результате чего выявляется ошибочность распространенной трактовки планиметрии Евклида как учения об инвариантах группы движений плоскости. Автор рассматривает один из возможных способов устранения данной ошибки с помощью построения иной группы преобразований. В статье излагаются необходимые сведения, относящиеся к геометрии циклоидальных кривых и геометрии треугольника. Большой объѐм статьи потребовал ее разбиения на две части.

1. ВВЕДЕНИЕ

Сущность математики является предметом тысячелетних споров. В полемическом задоре часто высказываются самые крайние точки зрения. Достаточно ярким примером является жаркий диспут между И. В. Арнольдом и Ю. И. Маниным [1]. Согласно утверждению Манина математика - это всего лишь отрасль лингвистики, занимающаяся в целом бессодержательными грамматическими упражнениями. Напротив, по мнению Арнольда, математику следует считать частью физики, то есть экспериментальной наукой [2].

Любой исследователь, опирающийся на исторические факты, должен признать, что, несмотря на полемические преувеличения, содержащиеся в словах В. И. Арнольда, он значительно ближе к истине, чем его оппонент. Доказательством могут стать факты, раскрывающие место математики в древних обществах, методы и цели исследований Демокрита и Архимеда, наконец, вся история математики семнадцатого, восемнадцатого и девятнадцатого века, теснейшим образом связанная с историей механики и физики.

Несомненно, математические объекты в определённом смысле реальны, хотя форма их существования весьма специфична.Реальность существования математических объектов состоит в независимости их свойств от субъективных мнений, как отдельных людей, так и любых человеческих сообществ. Реальный же объект не может быть полностью описан даже очень сложной и глубокой теорией, поскольку он, по известному выражению известного мыслителя, неисчерпаем[3].Непосредственно для математических объектов одним из подтверждений этого мнения является первая теорема Гёделя о неполноте. Можно считать, что каждая теория - это всего лишь одна из возможных, но всегда неполных, точек зрения на изучаемый объект.

Что касается характера изучаемых в математике объектов, они, несомненно, обладают различной степенью важности и уникальности. А. Н. Тюрин в предисловии к книге Феликса Клейна [4] следующим образом излагает мысли этого выдающегося учёного о математике: «Ткань математики широко и свободно разбегается листами отдельных теорий. Но есть объекты, в которых сходятся несколько листов, - своеобразные точки ветвления. Именно о таких объектах и следует говорить как об уникальных.

Высокая степень обобщённости математических теорий, как бы, нивелирует значение исторически исходных математических объектов. Однако жизнь постоянно подтверждает фундаментальность именно этих понятий, образов и представлений.К ним можно отнести натуральные числа, числовую прямую, плоскость и трёхмерное пространство. В определённом смысле именно они доступны для чувственного восприятия и экспериментального изучения, а, значит, являются неотъемлемой базой любого математического исследования.

Евклидова плоскость - важнейший для математики объект.Этот факт обусловлен множеством причин как математического, так и общекультурного порядка. Прежде всего, реально существуют и играют важную роль в человеческой жизни многочисленные чувственные прообразы плоскости, такие как водная, а часто и земная поверхность, натянутая ткань и т. д. Освоение пространства, связанное со становлением любой личности, во многом привязано к плоскости. При этом речь идёт как о движении человека по поверхностям, близким к плоскости, так и об изобразительной деятельности, знакомой каждому ребёнку. При этом и трёхмерное пространство и размещённые в нём тела вкладываются рисовальщиком в плоскость.

Евклидова плоскость, вернее её конечные куски, обозримы. По этой причине плоскость можно считать окном в платоновский мир совершенных идей. На ней (а, точнее, на её пусть и несовершенном аналоге - листе бумаги) можно начертить чертёж, приказать себе: «Смотри!- - и увидеть взаимосвязь, существующую между фигурами. Возможно, это обстоятельство и привело к созданию первой научной дедуктивной теории - геометрии Евклида (мы преимущественно будем говорить о планиметрии). Эта теория увязывает и объясняет большое количество различных фактов по принципу, сходному с принципом причинности. Недаром геометрия Евклида в течение тысячелетий служила образцом построения научной теории.Простота же доказательств сделала знакомство с ней одним из основных методов целенаправленного развития интеллекта европейского типа (теперь, возможно, более уместно говорить о староевропейском типе).

А. Н. Колмогоров постоянно подчёркивал связь математики с реальным миром, а также практическое значение математики [5]. Он отмечал, что «связи математики с техникой имеют характер применения уже созданных математических теорий к техническим проблемам. С этой точки зрения геометрия Евклида имеет непреходящее значение. Не только в технике, но и в быту всегда будут использоваться формулы для вычисления длин, площадей и объёмов. Многочисленные методы измерений, применяемые в геодезии, географии, астрономии, баллистике и т. д., основаны на евклидовой геометрии и тригонометрии.

Размеры и форма материальных предметов, а, следовательно, и их геометрические свойства исключительно важны в машиностроении и архитектуре. Все вопросы, связанные с построением изображений, в таких видах человеческой деятельности как живопись, черчение и картография, основываются на евклидовой геометрии. Механика и геометрия всегда были неразделимы. Кристаллография основывается на геометрическом фундаменте. И этот список можно легко продолжить.

На возражение, состоящее в том, что, например, кристаллография потребовала новых геометрических идей, можно ответить, что эти идеи всё же лежат в русле теории, изложенной Евклидом, и что «коллеги из другого колледжа (как назвал греческих математиков Литтлвуд [6]) смогли бы эти идеи понять.

Несмотря на огромную прикладную значимость геометрии Евклида, в чисто математическом плане она в настоящее время почти выпала из сферы интересов ведущих учёных. Так известный математик М. М. Посников на конференции, посвящённой проблемам философии и истории математики, утверждал, что евклидова геометрия как наука закончилась 2500 лет назад. Мы считаем, что это утверждение неверно, и постараемся обосновать свою точку зрения.

Геометрия Евклида является первой из математических теорий, изучающих плоскость, нона данный момент далеко не единственной такой теорией.Однако все более поздние теории, описывающие плоскость, зародились в её недрах и генетически теснейшим образом с ней связаны.

Книга Рене Декарта «Геометрия указала геометрам по новое направление. Итогом развития метода координат и реализации картезианской программы стали аналитическая геометрия, математический анализ функций одной переменной, дифференциальная геометрия. Каждая из этих взаимосвязанных теорий позволяет глубже понять геометрию плоскости.

В частности на основе методов Декарта возникла теория плоских кривых.Сейчас эта теория также считается далёкой от магистральных направлений современной математики, стремящейся к максимальной общности своих положений.А ведь именно теория плоских кривых стала зародышем алгебраической геометрии. Следует упомянуть и тот факт, что теория плоских кривых и сейчас не потеряла своего значения и может быть полезна для решения современных проблем математики. Чтобы убедиться в этом, достаточно ознакомиться с работой [7].

Дифференциальная геометрия теснейшим образом связана с теорией дифференциальных уравнений. Клейн следующим образом комментирует геометрические аспекты этой теории: «Сами дифференциальные уравнения представляют собой в дифференциальной геометрии выдающийся объект геометрических исследований; при этом можно говорить как о геометрическом смысле самого дифференциального уравнения, так в частности о том, каков геометрический смысл интеграции дифференциального уравнения [8]. Такой подход кардинально расширяет взгляд на геометрию плоскости, одновременно в корне меняя методы её изучения.

Отметим ещё и тот факт, что такой важнейший объект математики как поле комплексных чисел прочно привязан к плоскости. Видимо, уже Леонард Эйлер, задолго до Карла Фридриха Гаусса, ясно понимал это обстоятельство. История развития Клейном и Анри Пуанкаре теории автоморфных функций даёт впечатляющий пример роли геометрических идей в других областях математики. Кроме того, Клейн и Пуанкаре показали, что геометрия Лобачевского не только не противоречит геометрии Евклида, но и может быть успешно «смоделирована с помощью последней.

В каждой из перечисленных теорий речь по-прежнему идёт всё о той же плоскости. Хотя богатство содержания резко возрастает с увеличением числа новых теорий, вне схем и абстракций геометрия плоскости является единой. Однако на практике геометрия плоскости парадоксальным образом распадается на ряд специализированных разделов, которые постепенно теряют между собой непосредственную связь. Специалист по теории дифференциальных уравнений может не только не знать многих теорем геометрии треугольника, но и отзываться о них с известным пренебрежением. В то же время есть и иная точка зрения, состоящая в том, что подлинное познание объекта должно соединить все известные факты, какими бы разнородными они ни были.

Тем не менее, среди математиков весьма распространено мнение, что евклидова геометрия сыграла роль почвы, из которой выросли более общие теории, но при этом полностью потеряла своё значение в рамках математики, как развивающейся науки. На самом же деле внутренняя проблематика евклидовой геометрии стимулировала развитие математики даже и в двадцатом веке.

Значение внутренних проблем элементарной геометрии для развития математики в целом можно более объективно оценить, если вспомнить историю возникновения неевклидовых геометрий.Проблемы, связанные с пятым постулатом «Начал тысячелетиями захватывали математиков, пока не привели к открытию новых математических миров. В том же ключе можно рассматривать и работы Давида Гильберта по основаниям геометрии,оказавшие значительное влияние на развитие математической логики.

Следует вспомнить и неотъемлемую часть геометрии Евклида - задачи на построение. Эти задачи играли заметную роль в математике девятнадцатого века. Прежде всего, нельзя обойти вниманием первое открытие Гаусса, связанное с доказательством возможности построения циркулем и линейкой правильных многоугольников, число сторон которых выражается простыми числами Ферма.Последствия этого открытия для математики в целом чрезвычайно значительны.

Наоборот, идеи, возникшие в конце восемнадцатого и в начале девятнадцатого века за пределами геометрии, позволили не только развить новые геометрические теории, но и окончательно решить трудные проблемы классической геометрии. Так исследования Жозефа Луи Лагранжа и Эвариста Галуа, связанные с задачей решения алгебраических уравнений, ознаменовали возникновение теории групп. Соединение этой теории и идей проективной геометрии, также выросшей из геометрии Евклида, привело к созданию теории геометрических преобразований, общий смысл которой сформулирован в Эрлангенской программе Клейна. На этом же пути была решена проблема, связанная с разрешимостью задач на построение циркулем и линейкой.

Следует упомянуть также и раздел современной геометрии, использующий как новейшие математические теории, так и элементарные методы евклидовой геометрии. Речь идёт о геометрии в целом, разработанной, прежде всего, отечественной школой математиков, в том числе Б. Н. Делоне, А. Д. Александровым, А. В. Погореловым и Н. В. Ефимовым [9].

Как ни удивительно, но и геометрия Евклида в собственном смысле слова продолжала развиваться и в после греческий период, несмотря на возникновение новых теорий. К этому приложили руку математики всех калибров. Среди великих следует назвать Эйлера (прямая Эйлера, окружность девяти точек), Гаусса (прямая Гаусса), Якоба Штейнера (теорема об огибающей прямых Симсона, эллипс Штейнера, развитие теории геометрических построений).В то же время математики девятнадцатого века Фейербах и Морлей, открывшие теоремы Фейербаха и Морлея, известны только этими результатами.

В двадцатом веке едва ли не экспоненциально продолжалось накопление новых фактов. В первую очередь речь идёт о геометрии треугольника.Так или иначе, энтузиасты классической евклидовой геометрии и в наше время регулярно получают новые результаты, чаще всего укладывающиеся в рамки геометрии треугольника. Недаром в начале двадцатого века возник раздел планиметрии, называемый «новой геометрией треугольника [10].

В этой связи хочется упомянуть исследования Евгения Дмитриевича Куланина, который является одним из лучших специалистов по геометрии треугольника. Математические снобы могут усмехнуться, полагая, что проблемы такого рода находятся слишком далеко от модных направлений математики и слишком просты для них. Думается, что это не совсем так.

В геометрии треугольника поражает удивительное богатство содержания. С треугольником связаны сотни объектов, некоторые из которых мы упомянём, выбирая почти наугад:

• замечательные точки (например, общеизвестные точки пересечения медиан, биссектрис, высот, срединных перпендикуляров, и куда менее знаменитые точки Брокара, Лемуана, Торричелли, Фейербаха и т. д.);

• замечательные прямые (прямая Эйлера, бесконечное число прямых Симсона и т. д.);

• замечательные треугольники, порождаемые исходным треугольником (треугольник Наполеона, треугольник Морлея и т. д.);

• замечательные окружности (вписанная, описанная, вневписанные окружности, окружность Эйлера и т. д.);

• замечательные кривые (кривая Штейнера, являющаяся огибающей прямых Симсона, различные коники и кубики).

Охватить соответствующую проблематику с наскока невозможно. Знать геометрию треугольника может лишь специалист высокого уровня, каковым и является Е. Д. Куланин. Тут невольно вспоминаются слова Вольтера о том, что каждый должен возделывать свой сад.

Продолжая мысль Вольтера, сравним садовника и космонавта. Садовник, конечно, может обрести широкую известность, например, если он Иван Мичурин или Лютер Бербанк. Но слава к нему может прийти только в зрелые годы. И как же мало знаменитых садовников. А космонавтам честь, хвала и слава в молодые годы. Они ступали на другие планеты, на которых рядовые люди побывать не смогут. Они видели иные, неизвестные человечеству миры, безмерно холодные, безмерно горячие, лишённые жизни. Но вот вопрос. Будут ли нужны кому-нибудь эти миры, если на земле не останется садов? Элементарная геометрия - это тот сад, в который может войти каждый, если хватит упорства и трудолюбия. А тропа из этого сада ведёт на космодром.

Многолетнее общение с Куланиным помогло автору настоящей статьи составить некоторое представление о геометрии треугольника и заставило задуматься о причинах необыкновенной насыщенности этого раздела евклидовой геометрии. Кроме того, автору пришлось с удивлением обнаружить курьёзное, на его взгляд, утверждение, связанное с Эрлангенской программой Клейна и имеющее отношение к евклидовой геометрии вообще и геометрии треугольника в частности.

Данная статья является попыткой разобраться в этом вопросе.Попутно автор стремиться показать, сколь сложные конструкции на плоскости порождаются выбором обычного треугольника. При этом мы имеем в виду следующее. Пусть на плоскости выбраны три точки, не лежащие на одной прямой, а, значит, определяющие некоторый треугольник. Если построить некоторые из замечательных объектов перечисленных выше (все построить невозможно), возникнет некая порождаемая треугольником структура. Оценить её сложность читатель может самостоятельно.

Ниже используются некоторые факты геометрии треугольника, теории плоских кривых и теории геометрических преобразований. Для замкнутости изложения все теоремы доказываются в статье (начиная с параграфа 4).

2. ГЕОМЕТРИЯ ЕВКЛИДА В ЭРЛАНГЕНСКОЙ ПРОГРАММЕ КЛЕЙНА

Суть Эрлангенской программы Клейна коротко и ясно изложена в статье, первоначально напечатанной в Большой Советской Энциклопедии. В дальнейшем она перепечатывалась в Математической Энциклопедии [11] и Математическом энциклопедическом словаре. Таким образом, её содержание можно считать общепризнанной точкой зрения на Эрлангенскую программу. По этой причине ниже мы приведём данную статью полностью.

«ЭРЛАНГЕНСКАЯ ПРОГРАММА — единая точка зрения на различные геометрии (напр., евклидову, аффинную, проективную), сформулированная впервые Ф. Клейном (F. Klein) на лекции, прочитанной в 1872 в ун-те г. Эрланген (Германия) и напечатанной в том же году под назв. «Сравнительное обозрение новейших геометрических исследований (см. сб. «Об основаниях геометрии, М., 1956, с. 399—434).

Сущность Э. п. состоит в следующем. Евклидова геометрия рассматривает те свойства фигур, к-рые не меняются при движениях; равные фигуры определяются как фигуры, к-рые можно перевести одну в другую движением. Но вместо движений можно выбрать к.-н. иную совокупность геометрич. преобразований и объявить «равными» фигуры, получающиеся одна из другой с помощью преобразований этой совокупности; при этом приходят к иной «геометрии, изучающей свойства фигур, не меняющиеся при рассматриваемых преобразованиях. Введённое «равенство» должно удовлетворять следующим трём естественным условиям: 1) каждая фигура F «равна» сама себе; 2) если фигура F «равна» фигуре F', то и F' «равна» F; 3) если фигура F «равна» F', a F' «равна» F", то и F «равна» F". Соответственно этому приходится накладывать на совокупность преобразований следующие три требования: 1) в совокупность должно входить тождественное преобразование, оставляющее всякую фигуру на месте; 2) наряду с каждым преобразованием П, переводящим фигуру F в F', в совокупность должно входить «обратное» преобразование П₁, переводящее F' в F ; 3) с двумя преобразованиями П₁ и П₂, переводящих соответственно F в F' и F' в F", в совокупность должно входить произведение П₂П₁ этих преобразований переводящее F в F" (П₂П₁ состоит в том, что сначала производится П₁, а затем П₂). Требования 1), 2) и 3) означают, что рассматриваемая совокупность является группой преобразований. Теория, к-рая изучает свойства фигур, сохраняющиеся при всех преобразованиях данной группы наз. геометрией этой группы.

Выбирая по-разному группы преобразований, получают разные геометрии. Так, принимая за основу группу движений, приходят к обычной (евклидовой) геометрии; заменяя движения аффинными или проективным преобразованиями, — к аффинной или соответственно к проективной геометрии. Основываясь на идеях А. Кэли (A. Cayley), Ф. Клейн показал, что принятие за основу группы проективных преобразований, переводящих в себя нек-рый круг (или произвольное конич. сечение), приводит к неевклидовой геометрии Лобачевского. Ф. Клейн ввёл в рассмотрение довольно широкий круг других геометрий, определяемых подобным же образом.

Э. п. не охватывает нек-рых важных разделов геометрии, напр. риманову геометрию. Однако Э. п. Имела для дальнейшего развития геометрии существенное стимулирующее значение».

Итак, относительно геометрии Евклида мы можем извлечь из соответствующего текста два положения.

1. Приняв за основу группу движений плоскости (то есть группу преобразований, сохраняющих расстояния), мы приходим к евклидовой геометрии.

2. Евклидова геометрия изучает свойства фигур, сохраняющиеся при всех движениях плоскости.

Очевидно, что при подобной интерпретации евклидова геометрия превращается в набор тавтологий типа «А тождественно А-,поскольку любому здравомыслящему человеку ясно, что два равных треугольника обладают одинаковыми свойствами или, что то же самое, геометрические свойства треугольника при его перемещениях не изменяются.

В замечательной книге И. М. Яглома [12] цитируется определение геометрии, данное в классическом учебнике А. П. Киселёва: «наука, рассматривающая свойства геометрических фигур, называется геометрией-. Далее для обоснования мнения, что евклидова геометрия связана с группой движений, автор начинает критиковать расплывчатое понятие «свойство». При этом он задаётся вопросом, почему геометрия не рассматривает расстояние от вершин треугольника до края доски, хотя любому сколько-нибудь вменяемому человеку ясно, что речь идёт о свойствах именно треугольника, присущих ему как таковому, а не о привходящих обстоятельствах, связанных с учебным процессом. Не обязан же учитель географии, повесивший на доску карту мира, оговариваться, что бугорок, на доске рядом с картой не является величайшей вершиной мира.

Закончив обсуждение данного вопроса, И. М. Яглом переходит к изложению интереснейших точек зрения и методов решения геометрических задач. Геометрические преобразования прекрасно при этом работают, а вдумчивый читатель размышляет о свойствах именно треугольников, а не об окрестностях школы или дома, где он читает книгу.

Вряд ли кто-нибудь будет оспаривать тот факт, что теоремы, описывающие разнообразные свойства треугольников должны быть отнесены к евклидовой планиметрии. Приведём примеры общеизвестных теорем, доказательство которых разбирают школьники только что приступившие к изучению курса геометрии.

Начнём с теоремы о медианах. Три медианы треугольника пересекаются в одной точке и делятся точкой пересечения в отношении два к одному. Каждому человеку, понявшему доказательство ясно, что теорема верна для всех треугольников. Согласно концепции Клейна должна существовать группа преобразований, которая преобразует любой треугольник в любой, но при этом описанное в теореме свойство сохраняется. Такая группа преобразований очевидно существует. Однако это отнюдь не движения плоскости, а аффинные преобразования.

Напомним, что аффинным преобразованием называется преобразование плоскости, при котором каждая прямая переходит в прямую. При аффинном преобразовании сохраняется отношение отрезков, лежащих на одной прямой. Наконец, что особенно важно для нас, существует единственное аффинное преобразование, переводящее три произвольные точки А, В, С, не лежащие на одной прямой в произвольные точки А1, В1, С1, также не лежащие на одной прямой [13].

Таким образом, в геометрии треугольника имеются теоремы, которые описывают свойства треугольника инвариантные относительно группы аффинных преобразований. Все их можно доказать для правильного треугольника, а затем перенести на другие треугольники.

Однако, как известно каждому, в планиметрии есть и теоремы иного характера. В этом легко убедиться, если после теоремы о медианах вспомнить теорему о биссектрисах треугольника. Три биссектрисы треугольника пересекаются в одной точке. Очевидно, что точка пересечения биссектрис равноудалена от сторон треугольника и, по этой причине, является центром вписанной в треугольник окружности.

Утверждение о том, что в треугольник можно вписать окружность не относится к аффинной геометрии. Дело в том, что при аффинных преобразованиях окружность переходит в эллипс. Если правильный треугольник отобразить на треугольник произвольной формы, вписанная в правильный треугольник окружность перейдёт в так называемый эллипс Штейнера.

Описанная вокруг треугольника окружность также преобразуется в эллипс, который гомотетичен эллипсу Штейнера, вписанному в данный треугольник. Однако эллипсы это всё же не окружности.

Сделаем предварительный вывод. Геометрия треугольника, составляющая часть евклидовой геометрии плоскости, включает в себя как теоремы, описывающие инварианты аффинной группы преобразований, так и теоремы о свойствах присущих всем треугольникам, но инвариантами аффинной группы не являющимися.

Вернёмся теперь к описанным вокруг треугольников окружностям и попытаемся найти группу, которая переводит треугольники произвольной формы друг в друга, но сохраняет описанную окружность, не превращая её в эллипс. Для этой цели мы используем модель геометрии Лобачевского, разработанную Клейном.

Кратко изложим суть данной конструкции, поскольку она связана с ещё одним разделом математики, потерявшим свою былую популярность - проективной геометрией. Как указывается в [14], «ранее проективная геометрия была одним из центральных предметов в университетской программе.В наши дни роль проективной геометрии стала скромнее; не каждый студент, специализирующийся по математике, знаком с теоремами Паппа или Дезарга.

Проективную плоскость можно представить себе либо как расширение обычной евклидовой плоскости, возникающее после введения бесконечно удалённых точек, либо как пучок прямых в трёхмерном пространстве.

Первая точка зрения позволяет сохранять ощущение связи между традиционной евклидовой плоскостью и объемлющей её плоскостью проективной. При этом удаётся проследить как общие моменты, так и отличия между функционированием фигур и линий на евклидовой плоскости и их аналогами на плоскости проективной.

Вторая точка зрения удобна для введения и использования проективных преобразований в аналитической форме. Это связано с тем обстоятельством, что линейные преобразования трёхмерного пространства порождают проективные преобразования.

Здесь, однако, необходимо сделать следующие уточнения. Пусть задана евклидова плоскость π и точка О, не лежащая на ней. Пучок прямых с центром в этой точке взаимно однозначно отображается на проективную плоскость, являющуюся расширением евклидовой плоскости π. Если прямая α не параллельна плоскости π, то ей соответствует собственная (евклидова) точка А, являющаяся пересечением α и π. Если же прямая параллельна плоскости π, то ей соответствует одна из бесконечно удалённых точек проективной плоскости.

Сделаем первый шаг к созданию проективной системы координат. Зададим в трёхмерном пространстве декартову систему координат с центром в точке О. Рассмотрим теперь вектор αс координатами (а₁; а₂; а₃), исходящий из точки О. Он определяет некоторую прямую нашего пучка, соответствующую одной из точек проективной плоскости. На роль проективных координат соответствующей точки можно взять координаты (а₁; а₂; а₃).

Ясно, однако, что выбор вектора ане является однозначным. На эту роль можно взять и вектор λα, где λ - любое действительное число, не равное нулю. Таким образом, проективные координаты определяются неоднозначно. Это обстоятельство несколько затрудняет введение на проективной плоскости структуры алгебраического типа (аналога базиса линейного пространства).

Теперь выберем три любые прямые, принадлежащие пучку, но не лежащие в одной плоскости, и три соответствующих этим прямым вектора е₁, е₂, е₃. Тогда эта тройка векторов является базисом трёхмерного векторного пространства.Этим выбором мы устанавливаем взаимно однозначное соответствие между точками проективной плоскости и всеми линейными комбинациями векторов базиса. Однако этого мало. Вектора λ₁е₁, λ₂е₂, λ₃е₃ также образуют аналогичный базис, но в общем случае их линейные комбинации будут определять прямые пучка, не соответствующие прямым определяемым исходным базисом. Этого нужно избежать.

Фактически мы убедились, что трёх прямых нам недостаточно. Произвольным образом выберем четыре прямые, любые три из которых не лежат в одной плоскости. Пусть их направления определяются векторами е₁, е₂, е₃, е₄. В силу линейной зависимости этих векторов существуют неравные нулю коэффициенты, для которых λ₁е₁ + λ₂е₂ + λ₃е₃ + λ₄е₄ = 0. Более того, эти коэффициенты определяются с точностью до общего множителя.

Таким образом, выбор четырёх прямых пучка определяет на выбранных прямых четыре вектора  f₁ = λ₁е₁, f₂ = λ₂е₂, f₃ = λ₃е₃, f₄ = λ₄е₄, таких, что f₁ + f₂ + f₃ + f₄ = 0, длина которых определяется с точностью до ненулевого множителя λ.

Это обстоятельство позволяет определить проективное преобразование следующим образом. Кроме упомянутых выше четырёх прямых пучка выберем ещё четыре прямых, направления которых определяются векторами p₁, p₂, p₃, p₄.Тогда соответствующее линейное преобразование, переводящее вектора первого базиса в вектора второго, порождает взаимно однозначное отображение множества прямых пучка на себя. Но это и есть проективное преобразование плоскости.

Отметим, что наши не слишком строгие рассуждения подвели нас к формулировке важного свойства проективных преобразований плоскости. Оно состоит в том, что для любой упорядоченнойчетвёрки точек общего положения на проективной плоскости существует проективное преобразование, переводящее её в любой другую упорядоченную четвёрку точек общего положения.

Кэли и Клейном был установлен тот факт, что в рамках проективной схемы можно реализовать модель плоскости Лобачевского. Делается это так. На проективной плоскости выберем кривую второго порядка, которую назовём абсолютом. Внутренняя часть абсолютаи будет моделировать плоскость Лобачевского. Прежде чем двигаться дальше, поясним, что внешнюю часть кривой второго порядка на проективной плоскости заметают касательные к этой кривой.Группой движений при этом выступает подгруппа проективных преобразований, переводящих абсолют в себя. Рассмотрим вопрос о существовании подобных проективных преобразований и об их свойствах.

Как известно, уравнение а₁₁x² + а₁₂xy + а₂₂y² + b₁x + b₂y + c = 0 задаёт в декартовых координатах кривую второго порядка. Зададим на этой плоскости пять точек, никакие четыре из которых не лежат на одной прямой. Подставим их координаты этих точек в уравнение кривой второго порядка и получим систему из пяти линейных уравнений относительно неизвестных а₁₁, а₁₂, а₂₂, b₁, b₂, c. Эта система с точностью до множителя определяет неизвестные коэффициенты, а, значит, и единственную кривую второго порядка, проходящую через эти точки.

Поскольку проективное преобразование определяется четвёркой точек общего положения, а кривая второго порядка определяется пятью точками, возникает определённая проблема.

Эта проблема состоит в том, что для однозначной фиксации кривой второго порядка необходимо пять условий, а для фиксации проективного преобразования достаточно указать четыре точки. Таким образом, нужно указать пять геометрических объектов, связанных с кривой второго порядка, таких, чтобы ими определялись только четыре точки на плоскости.

Для решения данной проблемы можно использовать тот факт, что касательные к кривым второго порядка при проективном преобразовании переходят в касательные. Кроме того, если на кривой второго порядка зафиксирована точка и задана прямая, которая является касательной в этой точке, то этот факт может быть выражен аналитически. Соответствующее выражение может быть получено с помощью дифференцирования общего уравнения кривой второго порядка и последующей подстановки заранее заданных координат точки касания и производной. Очевидно, что будет получено линейное уравнение относительно неизвестных а₁₁, а₁₂, а₂₂, b₁, b₂, которое в системе линейных уравнений может заменить условие прохождения кривой через некоторую точку плоскости. Таким образом, в системе линейных уравнений условие прохождения кривой второго порядка через точку можно заменить на условие касания этой кривой и определённой прямой.

Зададим на кривой второго порядка два комплекта, каждый из которых содержит по три точки и по две касательных к этой кривой, проведенные в первых двух точках. Пусть первый набор содержит точки А₁, В₁, С₁ и касательные l_a1, l_b1, пересекающиеся в точке D₁, а второй набор - точки А₂, В₂, С₂ и касательные l_a2, l_b2, пересекающиеся в точке D₂.

Рассмотрим проективное преобразование, переводящее четвёрку точек А₁, В₁, С₁, D₁ в четвёрку точек А₂, В₂, С₂, D₂. Очевидно, что это преобразование переводит кривую второго порядка в себя. Кроме того, группа преобразований, переводящих кривую второго порядка в себя, позволяет любые три точки на этой кривой перевести в три другие точки на этой кривой. Наконец, отметим, что прямые при проективном преобразовании переходят в прямые.

Снова вернёмся к геометрии треугольника. Рассмотрим модель Клейна геометрии Лобачевского, у которой в качестве абсолюта взята окружность. Группа проективных преобразований, переводящих окружность-абсолют в себя, может перевести любые три точки А₁, В₁, С₁ на окружности любые три точки А₂, В₂, С₂ на той же окружности. Дополнив эту группу преобразованиями подобия, мы получим группу преобразований, переводящую произвольный треугольник и описанную вокруг него окружность в любой другой треугольник, сохраняя описанную окружность.

Итак, выяснилось, что к геометрии треугольника имеет отношение подгруппа группы проективных преобразований, к тому же связанная с неевклидовой геометрией.

По этому поводу сделаем следующее замечание. Доказательство того факта, что вокруг каждого треугольника можно описать окружность элементарно. Тем не менее, проведём его. Пусть задан треугольник АВС. Множеством точек равноудалённых от вершин А и В является прямая n (срединный перпендикуляр к отрезку АВ), а множеством точек равноудалённых от вершин В и С является прямая m (срединный перпендикуляр к отрезку ВС). Прямые n и m не являются параллельными, так как угол АВС меньше 180°. Таким образом, прямые n и m пересекаются в некоторой точке О, равноудалённой от вершин треугольника АВС.

Нельзя отрицать, что в доказательство основано на использовании евклидовой метрики. Однако никакого движения совмещающего два треугольника произвольной формы, а тем более переводящего одну описанную окружность в другую, не существует.

Более того, найденная нами группа проективных преобразований, сохраняя описанные окружности, к сожалению, искажает вписанные в треугольник окружности. Поясним это обстоятельство. При этом будем считать, что модель Пуанкаре геометрии Лобачевского более известна, чем модель Клейна, поскольку модель Пуанкаре связана с дробно-линейной функцией и конформными отображениями и изучается в курсе теории функций комплексного переменного.

В модели Пуанкаре также имеется окружность-абсолют. Однако прямыми являются дуги окружностей, лежащие внутри круга, ограниченного абсолютом, и ортогональные ему. Не ортогональные абсолюту дуги соответствуют эквидистантам. Окружности, изнутри касающиеся абсолюта, соответствуют орициклам. А окружности, целиком лежащие внутри абсолюта, являются окружностями геометрии Лобачевского. Используя этот факт, покажем, что окружностями в модели Клейна являются эллипсы.

В книге [15] описывается преобразование, переводящее модели Пуанкаре и Клейна друг в друга. При этом используется теорема о стереографической проекции (преобразовании проектирующем сферу, лежащую на плоскости, на эту плоскость из верхней точки сферы).Доказательство этой теоремы можно найти, например, в [16].

Эта теорема утверждает, что стереографическая проекция преобразует окружности, лежащие на сфере, в прямые или окружности, лежащие на плоскости. При этом стереографическая проекция сохраняет углы между кривыми.

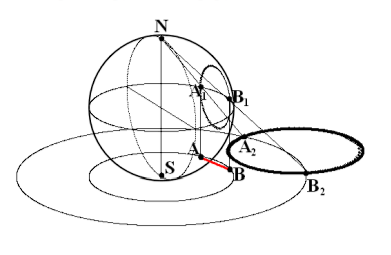
Пусть сфера касается окружности в точке S, а проектирование производится из диаметрально противоположной ей точки N (можно называть точки S и N полюсами сферы). Рассмотрим линию большого круга, параллельную плоскости (назовём её экватором). Тогда экватор и его внутренняя часть (см. чертеж) могут быть взаимно однозначно отображены на плоскость в две окружности с центром S. Одно из изображений - стереографическая проекция (она переводит точки А₁ и B₁ в точки А₂ и B₂), а второе - ортогональная проекция пространства на плоскость (она переводит точки А₁ и B₁ в точки А и В). И стереографическую проекцию, и проекцию ортогональную можно ограничить только на нижнюю полусферу. Соответствующие отображения обозначим через Ω и П.

Отметим также, что если окружность, лежащая на сфере, является пересечением этой сферы и некоторой вертикальной плоскости, то проекцией П она отображается в хорду абсолюта модели Клейна. Кроме того, эта окружность ортогональна экватору и по этой причине стереографической проекцией Ω отображается в окружность ортогональную абсолюту модели Пуанкаре.

Внутри малой окружности реализуем модель Клейна, а внутри большой - модель Пуанкаре. Легко видеть, что между двумя этими моделями есть связь. Так, например, модель Пуанкаре отображается на модель Клейна взаимно однозначным отображением Ω^-1П. Согласно только что сделанному нами замечанию при этом отображении прямые модели Клейна переходят в прямые модели Пуанкаре.

Кроме всего прочего, построенное нами отображение представляет собой изометрию[17]. Таким образом, оно переводит окружности Лобачевского из модели Пуанкаре в окружности Лобачевского из модели Клейна. Но, как уже указывалось выше, окружности Лобачевского из модели Пуанкаре является окружностями в обычном евклидовом смысле. Отображением Q^-1 они переносятся на сферу также в виде окружностей. Наконец отображение П превращает их в эллипсы. Исключением является тот случай, когда исходная окружность из модели Пуанкаре имеет общий центр с абсолютом. Легко понять, что соответствующая ей окружность из модели Клейна также является окружностью концентрической абсолюту.

Теперь мы можем показать, что группа проективных преобразований, сохранющих описанные окружности треугольника, превращает вписанные окружности в эллипсы. В абсолют модели Клейна впишем правильный треугольник, в который, в свою очередь, впишем окружность. Она будет одновременно окружностью Лобачевского из модели Клейна. Однако при любом преобразовании из нашей группы, окружность Лобачевского-Клейна перестаёт быть концентричной абсолюту, а, значит, переходит в эллипс.

Подведём предварительные итоги.

1. Согласно Эрлангенской программе Клейна теория, которая изучает свойства фигур, сохраняющиеся при всех преобразованиях данной группы называется геометрией этой группы.

2. Согласно ей же евклидова геометрия (в том числе и планиметрия) определяется группой движений, то есть группой преобразований, оставляющих евклидовы расстояния неизменными.

3. Естественное утверждение, что геометрия треугольника является разделом евклидовой геометрии, противоречит предыдущему положению.

4. В геометрии треугольника есть теоремы, описывающие некоторые свойства треугольника как инварианты аффинной группы преобразований.

5. В геометрии треугольника есть теоремы (теорема об описанной окружности), описывающие некоторые свойства треугольника как инварианты проективной группы преобразований, переводящей некоторую окружность в себя.

6. Однако та же самая проективная группа преобразований не обеспечивает инвариантность сходных утверждений (теорема о вписанной окружности).

3. ОБСУЖДЕНИЕ ПРИЧИН НЕПРАВИЛЬНОЙ ТРАКТОВКИ ЕВКЛИДОВОЙ ПЛАНИМЕТРИИ НА ОСНОВЕ ЭРЛАНГЕНСКОЙ ПРОГРАММЫ КЛЕЙНА

На примере простейших теорем из школьного курса геометрии мы только что показали, что неверно следующее утверждение: «Приняв за основу группу движений плоскости, мы приходим к евклидовой геометрии. Тем не менее, оно встречается в математической литературе, даже справочной. Постараемся понять причины этого недоразумения.

Прежде всего, следует отметить тот факт, что Эрлангенская программа Клейна только отчасти открывала новое направление исследований.Во многом же она наоборот подводила итог развития ряда геометрических теорий, выросших из евклидовой геометрии. Б. Л. Лаптев и Б. А. Розенфельд [18] выделяют три основных направления в развитии геометрии XIX века.

1. Совершенствование геометрических методов изучения обычного пространства (видимо, подразумевается трёхмерное евклидово пространство, отчасти отождествляемое с физическим пространством, или, по крайней мере, с пространством ньютоновской физики).

2. Расширение представлений о пространстве (неевклидовы геометрии, проективная геометрия, многомерные пространства, римановы пространства, топология многомерных многообразий).

3. Проникновение в геометрию алгебраических методов.

Первое из направлений упомянутыми авторами рассматривается как в значительной степени исчерпанное. Дальнейшее развитие геометрии сосредоточено на двух других направлениях.

Несомненно, что Эрлангенская программа Клейна затрагивает каждое из трёх направлений. И в той части (и части весьма значительной), где она была связана с первым направлением, Эрлангенская программа Клейна закрывала проблематику, связанную с «обычным пространством. Но именно в этой области и лежит представление о евклидовой геометрии как теории инвариантов группы движений.

Интенсивная творческая работа ведущих математиков ушла из этой области в сферу новых идей. Возможно, как раз по этой причине математическое сообщество не слишком углублялось в этот достаточно частный и периферийный для магистрального развития математики вопрос.

Тем не менее, одного этого замечания недостаточно для объяснения неправильной трактовки евклидовой планиметрии на основе Эрлангенской программы Клейна. По всей видимости, существовал целый комплекс подсознательных установок, заставивших принять неверное положение как очевидное и истинное. Попытаемся рассмотреть некоторые из них.

Прежде всего, следует вспомнить начавшуюся с момента выхода в свет «ГеометрииДекарта борьбу между геометрамисинтетического склада и аналитиками. К первым в XIX веке можно отнести Понселе (согласно его теории проективные свойства фигур - инварианты проектирований и сечений),Шаля (он следовал синтетической традиции Монжа, но использовал и алгебраические соотношения, включая использование мнимых чисел) и Штейнера (он являлся наиболее принципиальным противником алгебраических методов). Аналитические методы решения геометрических задач развивали Плюккер и Мёбиус [18].

В настоящее время развиваемые упомянутыми математиками методы можно рассматривать как взаимодополняющие, но сами они часто очень активно противостояли чуждым им методам. Например, Штейнер категорически отвергал применение методов алгебры и анализа в геометрии. С его точки зрения геометр должен постигать свою науку, созерцая воображаемые образы.

Клейн, описывая вклад Штейнера в математику [23], признаёт его выдающиеся достижения, но не может скрыть своей явной антипатии к выходцу из народной среды, недостаточно светскому для официальных кругов. Но и в рамках математики у Штейнера были затруднения при общении с некоторыми объектами. Клейн отмечает: «Однако, прежде всего, ему не доставало умения обращаться с мнимыми величинами. Он никогда не мог смириться с ними и употреблял такие выражения как «призрак или «царство теней геометрии.

Впрочем, и в наше время борьба между геометрией и алгеброй продолжается. Недаром же Герман Вейль сказал, что в душе каждого математика ангел геометрии борется с демоном алгебры. Почему Вейль связал геометрию с добрым и светлым началом, а алгебру с тёмным и злым? Алгебраические вычисления являются весьма мощным методом решения задач.Однако вычислитель достигает результата с однойпотерей - часто он не понимает причин, по которым математический факт именно таков, как он есть.Но и отказаться от вычислений, как показывает пример Штейнера, невозможно.

Так или иначе, метод Декарта привёл к революции в области математики. Вычисления превратились в локомотив, двигающий эту науку семимильными шагами. Именно метод координат позволил привести в геометрию алгебру, чтобы не созерцать и усматривать, а вычислять.

Координаты же представляют собой расстояния со знаком. Таким образом, мощный вычислительный подход основывается на использовании расстояний. А понятие расстояния является базовым для описания группы движений. Здесь, возможно, кроется одна из причин отмеченной нами ошибки. На подсознательном уровне могла возникнуть неверная импликация: любая теорема планиметрии может быть доказана с помощью вычислений, связанных с расстояниями, следовательно, планиметрия изучает инварианты группы движений. Это неверно, но этот вопрос для математики уже стал периферийным.

В очередной раз повторимся: ошибка могла возникнуть только по причине того, что речь шла не о магистральных путях математики, а о второстепенных для математического сообщества вопросах. Девятнадцатый век - это и век математических революций, и век закрытия ряда проблем, остававшихся тысячелетиями нерешёнными (квадратура круга, трисекция угла, удвоение куба, проблема пятого постулата Евклида). Не удивительно, что не только многие старые теории уходили в тень, но и новые направления, едва возникнув, тут же теряли свою актуальность.

Назовём некоторые прорывные области математики девятнадцатого века, не претендуя на полноту и систематичность.

• Создание геометрии Лобачевского и поток геометрических теорий, полностью видоизменивших геометрию (проективная геометрия, неевклидовы пространства, многомерные пространства, создание векторных методов изучения пространства, невиданный прогресс дифференциальной геометрии, выделение алгебраической геометрии).

• Создание теории групп и решение неразрешимых ранее проблем, поставленных ещё греками.

• Возникновение современной алгебры, в корне отличной от алгебры, связанной с решением уравнений.

• Развитие новых методов в теории чисел.

• Развитие новых методов в теории вероятностей (например, цепи Маркова).

• Всестороннее развитие анализа, включая его обоснование.

• Создание топологических методов.

• Создание математической логики.

• Создание теории множеств Кантора.

• Проникновение идей теории множеств, теории групп и топологии во все области математики.

• Создание физических теорий, имеющих глубокое математическое содержание (теория электромагнетизма, статистическая физика, специальная теория относительности в варианте Лоренца-Пуанкаре).

Не удивительно, что крупные математики девятнадцатого века считали себя одновременно и философами. Им пришлось осмысливать тот невероятный прогресс своей науки, который достигался их усилиями и на их глазах.

Интересно на этом впечатляющем фоне рассмотреть возникновение геометрии Н. И. Лобачевского. Она, несомненно, витала в воздухе. Варианты её построения кроме Лобачевского имели Я. Бояи и Гаусс. У них были такие знаменитые предшественники как Омар Хайям и Ламберт, который высказал идею об осуществлении особой геометрии на мнимой сфере [24]. Но Гаусс даже не пытался опубликовать свои разработки в этой области, а Лобачевский был не только не понят, но и безжалостно осмеян. Прискорбно, что в активном неприятии Лобачевского участвовал первый крупный отечественный математик М. Б. Остроградский. Пригретый Лобачевским итальянец Больцани, которому учёный диктовал свою «Пангеометрию, назвал её бредом сумасшедшего [25].

Даже теорию множеств большинство математиков встретило с восторгом, хотя именно она поколебала всё, на первый взгляд, стройное здание математики. Почему же с таким трудом в математику пришла геометрия Лобачевского? Дело в том, что она перевернула представление о внутренних связях математики и реального мира.

После того, как были признаны непротиворечивыми две необычайно близких системы аксиом (они отличались лишь одной аксиомой), возникли два непохожих друг на друга геометрических мира. Тем самым, геометрия Лобачевского опровергла мнение Канта об априорном, не зависящем от опыта характере геометрических понятий. По словам Гаусса, геометрия приблизилась к механике, науке экспериментальной.

Поток геометрических исследований девятнадцатого века, внешне крайне разнородный, вылился в неожиданный результат. Оказалось, что геометрий бесконечно много. Раньше это обстоятельство уже давало о себе знать. Существовали сферическая геометрия и тригонометрия. Однако они не воспринимались как новые геометрические теории, поскольку сфера вложена в трёхмерное евклидово пространство. Ситуация изменилась, когда Гаусс создал внутреннюю геометрию поверхностей.

Отметим, что рядом с математическими исследованиями возникали и многочисленные мистические фантазии на геометрические темы. Так психолог и физиолог Густав Теодор Фехнер придумал двухмерные существа, подобные теням. Хорошо известна в наше время книга английского священника Эдвина Эбботта «Флатландия, описывающая плоскую страну, населённую плоскими людьми.

При современном изложении геометрическую теорию Гаусса охотно дополняют идеями этих фантастов: «Представим себе двумерное живое существо, обладающее достаточным интеллектом для того, чтобы производить точные измерения на поверхности, где оно обитает, но лишённое возможности представить себе третье измерение [6]. Цель плоского существа изучить геометрию своего плоского пространства. Не вдаваясь в подробности, констатируем, что подход Гаусса уже создал бесчисленные геометрии, связанные с отдельными поверхностями. На этом пути была получена интерпретация геометрии Лобачевского на псевдосфере, созданная Бельтрами и доказавшая непротиворечивость геометрии Лобачев- ского.Риман далеко продвинул подход Гаусса, введя в математику понятие многообразия, то есть множества объектов, с которым связана непрерывная система координат. Тем самым им были рассмотрены многомерные аналоги физического пространства, в которых вводилась метрика.

Гельмгольц поставил вопрос о возможности движения в таких пространствах, ибо ис- покон веков пространство - это поле, предназначенное для перемещения чего-либо. Его не совсем корректные рассуждения сделал вполне строгими Софус Ли, основываясь на разработанной им теории непрерывных групп.

Итак, в девятнадцатом веке была создана совершенно новая концепция пространства, которая содержала в себе и обобщенное понимание движения, связывая его с группами геометрических преобразований.

Эрлангенская программа Клейна была одним из этапов соответствующего процесса. Дадим обширную цитату из статьи «Теория групп и геометрия великого математика уже двадцатого века Эли Картана [26]. Интересно, что и он допускает ту же неточность в отношении геометрии Евклида.

«Как известно, основная идея Клейна может быть связана с наиболее древними понятиями науки. Элементарная геометрия изучает свойства фигур, которые не зависят от их частного положения в пространстве. Прошло немало столетий прежде, чем эта несколько неопределенная формулировка была переведена на точный язык: свойства, изучаемые элементарной геометрией, являются теми, которые остаются инвариантными относительно некоторой совокупности преобразований, образующей группу движений. Аксиома, по которой две фигуры, равные третьей, равны между собой, в несколько отвлеченной форме и выражает свойство движений образовывать группу. Проективная геометрия, являвшаяся сначала одной из глав элементарной геометрии и превратившаяся, при дальнейшем развитии в самостоятельную научную дисциплину, с точки зрения Клейна есть изучение свойств фигур, инвариантных относительно некоторой совокупности преобразований (проективных преобразований), образующих группу.

Вообще всякая группа непрерывных преобразований определяет самостоятельную геометрию. Эта геометрия, если рассматривать переменные, преобразуемые группой, как величины, определяющие точку пространства соответствующего числа измерений, изучает свойства фигур, инвариантные относительно преобразований группы G, причем эти последние играют такую же роль, как движения в евклидовой геометрии или проективные преобразования в геометрии проективной. Группа G называется фундаментальной группой данной геометрии. Таким образом, получается аффинная геометрия, конформная или анал- лагматическая геометрия, геометрия Лагерра (см. [8]), эрмитова(см. [8]) и т. д.

Для удобства выражения присоединяют к слову «пространство эпитет, характеризующий фундаментальную группу изучаемой геометрии; так, говорят: евклидово пространство, проективное пространство и т. д.

Все так называемые пространства Клейна являются однородными в том смысле, что их свойства инвариантны относительно преобразований соответствующей фундаментальной группы: эта группа служит, в некотором смысле, мерой однородности пространства. Пространство вполне однородное ± это такое пространство, фундаментальная группа которого является бесконечной группой всех непрерывных преобразований: это ± топологическое пространство; геометрические свойства фигур здесь сравнительно мало разнообразны; они становятся уже более примечательными, если за фундаментальную группу принять бесконечную группу всех непрерывных дифференцируемых преобразований.

Картан даёт очень ясную картину того понимания геометрических структур, которое достигается в Эрлангенской программе: топологическое пространство и группа непрерывных преобразований, то есть фундаментальная группа.

Фундаментальная группа является группой, аналогичной группе евклидовых движений. С точки зрения обитателя реального трёхмерного пространства движение есть перемещение предмета из одного места в другое. Понятие фундаментальной группы даёт несколько иной акцент понятию движения. Пусть в пространстве задано некоторое множество точек, называемое фигурой. Например, пусть на евклидовой плоскости выделен один единственный треугольник. Применим к фигуре все преобразования входящие в фундаментальную группу, тогда будут получены все эквивалентные исходной фигуре образы. В случае нашего примера с помощью движений будут «очерчены все треугольники, равные исходному во всех возможных положениях.

Таким образом, фундаментальная группа в понимании Картана задаёт отношение эквивалентности для фигур. При этом фигуры являются эквивалентными между собой и не имеют никаких отличий. Откуда же могут взяться инварианты? Для разъяснения обратимся к проективной геометрии. Действие группы проективных преобразований происходит на фоне уже существующей группы движений. Конфигурации, возникающие при проективных преобразованиях эквивалентны между собой, но с точки зрения евклидова пространства, которое всё же всегда присутствует в проективном пространстве, они различны. Именно здесь появляется возможность получения инвариантов. Например, таковым является двойное или сложное отношение четырёх точек, лежащих на одной прямой. У евклидовых же движений такого фона нет. И нет его только у евклидовой геометрии.

Рассмотрим одну из интерпретаций планиметрии Лобачевского, принадлежащих Кэли (абсолютом является произвольная кривая второго порядка, фундаментальной группой - подгруппа проективных преобразований, переводящих абсолют в себя), Клейну (отличие от интерпретации Кэли в том, что абсолютом является окружность) или Пуанкаре (абсолютом является окружность, фундаментальной группой - группа конформных преобразований, переводящих внутренность абсолюта в себя). Все они имеют тот же самый фон - евклидову плоскость.

По этой причине даже то действие, которое мы назвали чуть выше «очерчиваниемфигур, может рассматриваться, как некое геометрическое исследование. Например, в модели Пуанкаре необходимо показать, что прямые являются дугами окружностей, ортогональных к абсолюту, а окружности - окружностями, лежащими внутри абсолюта. В этой части геометрия Лобачевского может рассматриваться как поиск инвариантов фундаментальной группы. Но как только мы перейдём к геометрии треугольника на плоскости Лобачевского, ситуация изменится, поскольку не все треугольники равны друг другу. В этом смысле мы видим, что определение Клейна сужает реальное содержание, по крайней мере, таких геометрических теорий как геометрия Евклида и геометрия Лобачевского. Тут уместно вспомнить слова Гёте: «Суха, мой друг, теория везде, а древо жизни пышно зеленеет.

Видимо, теперь можно назвать ещё одну причину неправильной трактовки геометрии Евклида. Она состоит в некотором пренебрежении (в чём-то вполне естественном) к многообразию простых и достаточно конкретных фактов.

В заключение этого раздела отметим, что можно рассматривать геометрические пространства преимущественно с алгебраических позиций. Такую возможность предоставляет использование координат. Например, Кэли разрабатывал проективную геометрию аналитически [18].

В этом случае возникает несколько иной подход к поиску инвариантов, основанный не столько на выявлении свойств тех или иных образов в духе Штейнера, сколько на выявление числовых инвариантов. Элементарным примером является теория инвариантов, связанная с одним из разделов аналитической геометрии на плоскости, а именно с общей теорией линий второго порядка [27].

Обсуждение вычислительной линии можно было бы продолжить, упомянув тензорный анализ или теорию инвариантов, но мы ограничимся цитатой, взятой из статьи Эли Картана «Роль Франции в развитии математики [28]. В ней хорошо показана важность сохранения в математике традиционного геометрического содержания, сохраняющего эту науку живой.

«Гастон Дарбу (1847 - 1917) был одновременно специалистом по анализу и геометрии. Я оставлю в стороне его исследования по анализу, несмотря на их большое значение, и на то, что в некоторых из них он был предшественником важных открытий. Своей славой Дарбу обязан, прежде всего, своим трудам по геометрии. Дарбу не относился ни к тем геометрам, которые отказываются от чистой красоты геометрии для того, чтобы заменить ее аналитическими выкладками, ни к тем специалистам по анализу, которые сводят геометрию к последовательности вычислений и которые не интересуются их геометрическим смыслом. В этом смысле он был продолжателем Монжа, соединявшего очень умелое использование анализа с очень тонкой и очень развитой геометрической интуицией. Его методы всегда отличались редким изяществом и совершенным образом сочетались с особенностями рассматриваемых случаев.

В частности живая математика (таково название одной из книг Я. И. Перельмана) должна быть связана со всем родом человеческим, должна служить ему, в том числе и обогащая знаниями, делая всех умнее. Пусть для этого понадобится всего-навсего теорема о средней линии треугольника. При этом сообщество математиков-профессионалов не должно превращаться в секту высокомерных и презирающих всё и вся сектантов, служителей искусству для искусства.

Увы, такая тенденция есть. Высказывание Манина, открывающее нашу статью, хотя бы частично подтверждает это. Для ознакомления с экстремистскими взглядами (уже в значительной степени обрушившими математическое образование, и не только во Франции) предлагаем читателю прочитать введение к книге [29].

Мы же переходим к рассмотрению «архаичных вопросов, связанных с геометрией треугольника. Начинаем при этом с изложения элементарной, но наш взгляд весьма красивой теории циклоидальных кривых. При этом, хотя нам не понадобится весь арсенал теорем, из- ложенныйдалее, мы излагаем эти вопросы подробно, считая их достаточно интересными сами по себе. Далее будут доказаны некоторые теоремы геометрии треугольника, после чего будет построена группа, преобразующая произвольные треугольники друг в друга.

4. КАРДИОИДА

В наших дальнейших построениях важную роль будут играть кривые образованные следующим образом. Пусть у нас имеются лекала двух плоских кривых. Закрепим одно из лекал на плоскости, а второе приложим к нему и будем катить по первому лекалу без проскальзывания. Если на втором лекале закреплено перо, оно будет вычерчивать некую линию. Наиболее известным примером подобной кривой является циклоида. При её построении роль первого лекала играет прямая линия, роль второго - окружность, а перо закреплено непосредственно на катящемся ободе.

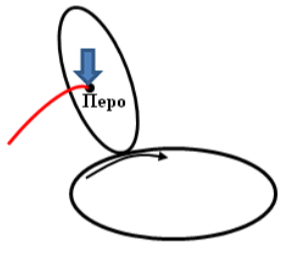
На примере циклоиды укажем на два обстоятельства, характерных для всех кривых, получаемых с помощью качения. Пусть точка А, лежащая на окружности и на которую окружность опирается в исходный момент, при повороте на угол φ перейдёт в положение А₁. Окружность при этом будет опираться на точку В. Тогда математически точное определение качения без проскальзывания состоит в том, что длина отрезка АВ равна длине дуги А₁В. Таким образом, соприкоснувшиеся при качении дуги обеих кривых имеют равную длину.

Второе обстоятельство таково. Пусть перо, вычерчивающее, кривую находится в точке Р, а окружность опирается на точку В. Тогда точка В в данный момент неподвижна, а, значит, мгновенное движение катящейся окружности является вращением этой окружности вокруг точки В. Из этого следует, что мгновенная скорость точки Р (как, впрочем, и всех остальных точек) перпендикулярна отрезку соединяющему эту точку с центром вращения, то есть она перпендикулярна отрезку ВР. Но это означает, что касательная к циклоиде перпендикулярна отрезку ВР.

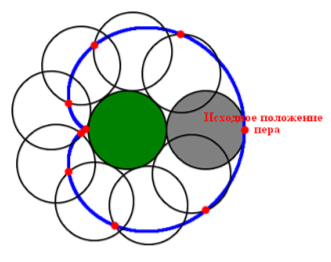
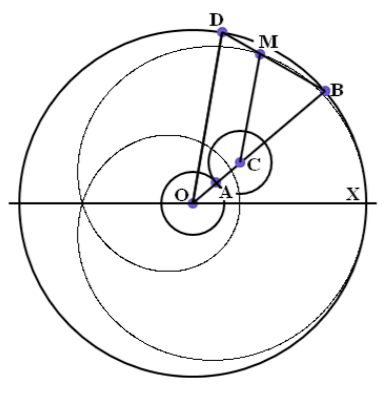
Если закрепить окружность и катить по ней равную ей окружность с пером на ободе, будет построена одна бесконечного числа улиток Паскаля, за сходство сердцем названная кардиоидой.

Изучим некоторые свойства кардиоиды, которые дальнейшем перенесём не только на улитки Паскаля, но и на более широкий круг кривых, образованных качением одной окружности по другой. При этом будем считать исходным положением катящейся окружности и пера то, которое указано на рисунке.

Кардиоида, как и прочие улитки Паскаля, является благодарным предметом для исследователя. Все доказательства её свойств основаны на простейших теоремах элементарной геометрии.

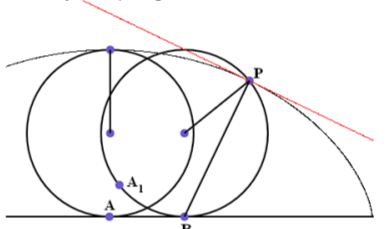
Теорема 1. Пусть точки В и D движутся по окружности радиуса 3r с постоянными скоростями, причём скорость точки D в два раза больше скорости точки В. Точка М,которая отсекает треть хорды BD (ВМ = 1/3 BD) описывает кардиоиду, а любая хорда BD является касательной к этой кардиоиде.

Доказательство. Кардиоида построена с помощью неподвижной окружности радиуса r с центром О и катящейся окружности радиуса r с центром С. Пусть ∠ ВОХ = u. Выберем точку D так, чтобы ∠ BOD = u Соприкоснувшиеся при качении дуги обеих окружностей имеют длину ru. Из исходного положения Х перо переместилось в точку М. При этом горизонтальная линия ОХ перешла в линию ОВ, а перо же за счёт качения отклонилось от этой линии на угол u, то есть ∠ ВСМ = u. Треугольники OBD и СВМ являются равнобедренными и имеют углы при вершинах равные u. Значит у них равны и углы при основании, то есть . Из этого следует, что точка М лежит на хорде BD. Из подобия названных треугольников следует, что ВМ = 1/3 BD.

Далее ∠ ВАМ = u/2, как вписанный в окружность и опирающийся на дугу, соответствующую центральному углу u. Таким образом, треугольник МАВ является прямоугольным, то есть хорда BD перпендикулярна отрезку АМ, исходящему из неподвижный в данный момент точки А. Как указано выше, это означает, что хорда BD является касательной к этой кардиоиде в точке М. Теорема доказана.

Теорема позволяет без всяких проблем получить параметрические уравнения кардиоиды. Точка В имеет координаты (3r*cosu; 3г*sinu), а точка D - координаты (3r*cos2u; 3г*sin2u). Из теоремы следует, что отрезки с концами, имеющими соответствующие координаты, являются огибающими кардиоиды. Координаты точки М вычисляются по формулам, которые и являются нужными уравнениями:

Приведём простую компьютерную программу на языке SmallBasic, которая иллюстрирует правильность наших результатов и строит на экране и кардиоиду и её огибающие.

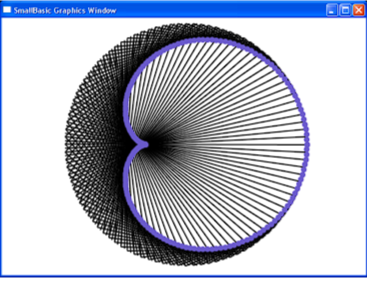
pi = Math.Pi

x0 = 320

y0 = 220

r = 70

'Огибающие

For u = 0 To 2*pi Step pi/100

xb = x0 + 3*r*Math.Cos(u)

yb = y0 - 3*r*Math.Sin(u)

xd = x0 + 3*r*Math.Cos(2*u)

yd = y0 - 3*r*Math.Sin(2*u)

GraphicsWindow.DrawLine(xb,yb,xd,yd)

EndFor

'Кардиоида

For u = 0 To 2*pi Step pi/100

xb = x0 + 3*r*Math.Cos(u)

yb = y0 - 3*r*Math.Sin(u)

xd = x0 + 3*r*Math.Cos(2*u)

yd = y0 - 3*r*Math.Sin(2*u)

x = xb + (xd - xb)/3

y = yb + (yd - yb)/3

GraphicsWindow.FillEllipse(x - 5,y - 5,10,10)

EndFor

Отметим в полном смысле очевидную особенность кардиоиды, которая будет важна в дальнейшем. Речь идёт о наличии у кардиоиды точки излома, называемой в дифференциальной геометрии точкой возврата (кривая входит в эту точку и тут же уходит из неё в обратном направлении).

Дадим два определения, следуя [19]. «Подэрой данной кривой относительно какой- либо точки плоскости называется новая кривая, представляющая собой геометрическое место оснований перпендикуляров, опущенных из этой точки на касательные к заданной кривой.

Пусть заданы некоторая кривая, называемая базисом конхоиды; точка на плоскости, называемая полюсом конхоиды, и фиксированное число а. Тогда конхоидой называется множество точек, лежащих на прямых, проходящих через полюс, и удалѐнных от точки пересечения с базисом на расстояние а.

Теорема 2. Кардиоида является подэрой некоторой окружности относительно точки возврата.

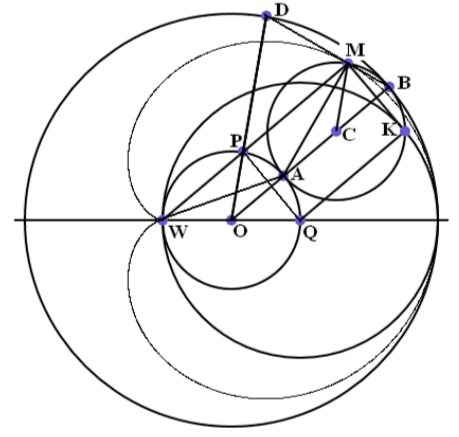
Доказательство. Будем использовать все обозначения, принятые в доказательстве теоремы 1. Построим окружность радиуса 2r, с центром Q, являющимся пересечением горизонтальной прямой и неподвижной окружности. Построенная нами окружность проходит через точку возврата W и касается кардиоиды в начальной точке её построения. Именно для этой окружности кардиоида и является подэрой. Чтобы доказать этот факт, соединим точку М, лежащую на кардиоиде, с точкой возврата W.

Рассмотрим треугольники AOW и АСМ.

Они равны, поскольку эти треугольники являются равнобедренными с боковой стороной r, и имеют внешний угол при вершине, равный u. Углы при основании у них равны u/2.

Из этого следует, что треугольник AWM также является равнобедренным, а угол при вершине у него равен π - u. Значит, и у него углы при основании равны u/2. Но ∠ MWO = ∠ AWO + ∠ AWM = u/2 + u/2 = u. Таким образом, прямая WM параллельна прямой ОВ.

Прямая WM пересекает неподвижную окружность в некоторой точке Р. Поскольку ∠ MWO = ∠ PWO = u, дуга, на которую опирается ∠ MWO, вписанный в неподвижную окружность, имеет угловую меру 2u. Таким образом, точка Р лежит и на прямой OD. Из этого факта мы можем сделать следующий вывод: четырёхугольник ОРМС является параллелограммом, поскольку параллельность прямых OD и СМ, а также прямых WM и ОВ мы установили ранее. Значит, длина отрезков РМ и ОС одинакова и равна 2r.

Далее, ∠ WPO является прямым, так как опирается на диаметр неподвижной окружности. Проведём радиус QK окружности, построенной нами в начале доказательства, параллельный прямой WM. Он будет перпендикулярен прямой QP, а поскольку РМ = QK = 2r, четырёхугольник QPMK является прямоугольником. Прямая МК перпендикулярна радиусу QK, а, значит, является касательной к окружности с центром в точке Q и радиусом 2r.

Итак, точка кардиоиды М является основанием перпендикуляра, опущенного из точки возврата W на касательную МК к соответствующей окружности. Теорема доказана.

Попутно нами получен ещё один результат, который просто нужно заметить.

Теорема 3. Кардиоида является огибающей окружностей, центры которых лежат на неподвижной окружности, а сами они проходят через точку возврата.

Доказательство. Из равенства треугольников AOW и АСМ следует, что AW = АМ. Кроме того, отрезок АМ перпендикулярен касательной к кардиоиде BD. Теорема доказана.

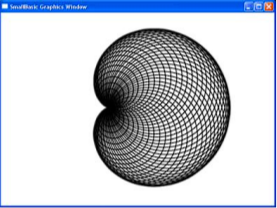
Используя эту теорему, приведём программу на языке SmallBasic, которая строит на экране и кардиоиду как огибающую соответствующих окружностей.

pi = Math.Pi

x0 = 320

y0 = 220

r = 70

For u = 0 To 2*pi Step pi/30

xx = x0 + r* Math.Cos(u)

yy = y0 — r* Math.Sin(u)

rr=Math.SquareRoot(Math.Power(x0-r-xx,2)+Math.Power(y0-yy,2))

GraphicsWindow.DrawEllipse(xx - rr,yy - rr, 2*rr, 2*rr)

EndFor

Теорема 4. Кардиоида является конхоидой, базисом которой является неподвижная окружность, полюсом - точка возврата, а расстояние от базиса до точек кардиоиды равно 2r.

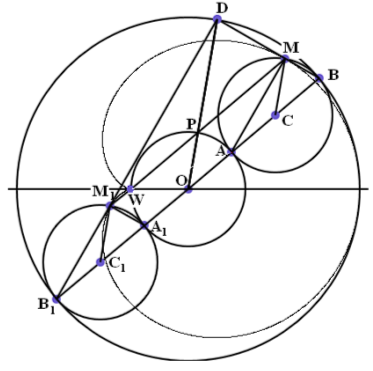
Доказательство. Мы рассматривали положение катящейся окружности в момент, когда линия центров ОС наклонена к горизонтали под углом u. Дополним нашу картину изображением катящейся окружности, соответствующей наклону линии центров ОС₁ под углом л + u. Очевидно, что точки О, А, С, В и соответствующие им точки второго положения А₁, С₁, B₁ расположены на одной прямой.

Как мы уже доказали, прямая WW параллельна прямой ОС. Точно также прямая Wi параллельна прямой ОС₁, а, значит, прямые WМ и WM₁ как параллельные одной прямой совпадают.

Далее, в теореме 2 было доказано, что РМ = 2r. Точно

также РМ₁ = 2r. Но тем самым мы как раз и установили, что выполняется условие доказываемой теоремы. Таким образом, кардиоида является конхоидой неподвижной окружности.

Что касается точки D₁, то она определяется углом 2-(л - u) или 2u после отбрасывания полного оборота. А, значит, точка D₁ совпадает с точкой D. Но это значит, что касательные к кардиоиде BD и BD1 перпендикулярны друг другу, так как угол BDB₁ опирается на диаметр ВВ₁. Таким образом, верна следующая

Теорема 5. Касательные к кардиоиде, проведённые через концы хорды данной кардиоиды, проходящей через точку возврата перпендикулярны между собой. Геометрическим местом вершин соответствующих прямых углов является окружность с центром О и радиусом 3r.

Сделаем ещё несколько замечаний, которые связаны со стандартными формами описания кривых, принятыми в дифференциальной геометрии.

Используя тот факт, что кардиоида является конхоидой неподвижной окружности, выведем её уравнение в полярных координатах. За полюс полярной системы координат примем точку возврата кардиоиды W. Поскольку угол MWT равен u, длина отрезка WP очевидно равна 2т cosu. Длина же отрезка WM, являющаяся расстоянием от полюса W до точки М, лежащей на кардиоиде, равна 2т(1 + cosu). Таким образом, уравнение кардиоиды в полярных координатах имеет вид ρ = 2·r·(1+cosu).

Перейдем от полярных координат к декартовым, имея ввиду, что  и . В результате получим, что уравнение кардиоиды имеет вид:

(x² + y² - 2rx)² - 4r²(x² + y²) = 0.

Значит, кардиоида является кривой четвёртого порядка, то есть, кроме всего прочего, она принадлежит к классу алгебраических кривых.

Практически все наши результаты, полученные для кардиоиды, без труда переносятся на улитки Паскаля.

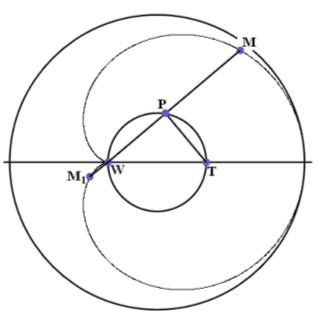
Однако прежде, чем переходить к изучению улиток Паскаля, рассмотрим два важных и взаимосвязанных понятия дифференциальной геометрии. Речь идёт об эволютах и эвольвентах. Разъясним, что представляет собой эвольвента. При этом мы используем механический образ, избегая точных математических определений. Нам понадобятся белая бумага, карандаш, нитка, чайная чашка и фотоаппарат. Для того, чтобы объяснить, что изображает фотография, процитируем книгу [19]: «Эвольвенту заданной кривой можно вычертить непрерывным движением. Для этой цели изготовляется шаблон заданной кривой. В какой-либо точке её закрепляется конец нерастяжимой нити, которую обвёртывают вокруг кривой, а на другом её конце закрепляют чертящее остриё. Если теперь развёртывать нить, оставляя её всегда в натянутом состоянии, то острие вычертит эвольвенту. На фотографии строится эвольвента окружности.

Рассмотрим процесс построения эвольвенты более внимательно. При её построении нить «стекает с абриса кривой. Предположим, что в одной из точек она может зацепиться за гвоздик, а может и не зацепиться. Как мы узнаем о том, что произошло с нитью? Мы будем следить за движением карандаша, который либо продолжит вычерчивать эвольвенту (нить не зацепилась), либо начнёт вычерчивать окружность (нить зацепилась). Но на фиксацию данного факта нужно время. Непосредственно же в момент осуществления того или другого варианта невозможно узнать, что произошло. Таким образом, движение карандаша по эвольвенте и по окружности неразличимы в течение очень го промежутка времени.

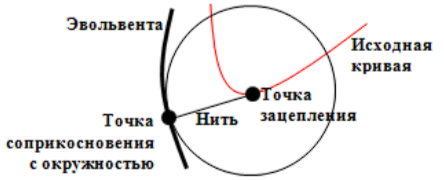
Если вдуматься в ситуацию, получается, что эвольвента и соответствующая окружность соприкасаются. Значит, у них общая касательная. А, кроме того, на малом участке дуга эвольвенты мало отличается от дуги окружности. Окружность как бы моделирует изгиб кривой. По этой причине радиус окружности называется радиусом кривизны кривой.

И ещё очень важно то, что касательная к окружности (а, значит, и касательная к эвольвенте) перпендикулярна радиусу, то есть перпендикулярна к нити. А поскольку наши рассуждения применимы к любой точке эвольвенты, мы можем утверждать, что нить при вычерчивании эвольвенты, является нормалью к ней. Таким образом, касательные к исходной кривой являются нормалями к эвольвенте. Это означает, что зная эвольвенту, можно восстановить исходную кривую. Её принято называть эволютой. По заданной эвольвенте можно построить эволюту как огибающую нормалей.

Отметим ещё и следующий факт. Центры окружностей, моделирующих изгибы эвольвенты в каждой её точке, лежат на эволюте и полностью её заметают. Каждый из этих центров называется центром кривизны соответствующей кривой в определённой точке. Таким образом, эволюта кривой является множествомили, как говорили когда-то, геометрическим местом центров её (то есть исходной кривой) кривизны.

Теперь обратимся к задаче о построении эволюты кардиоиды, то есть к построению огибающей нормалей кардиоиды.

Теорема 6. Эволютой кардиоиды является также кардиоида, гомотетичная исходной относительно центра неподвижной окружности с коэффициентом, равным -1/3.

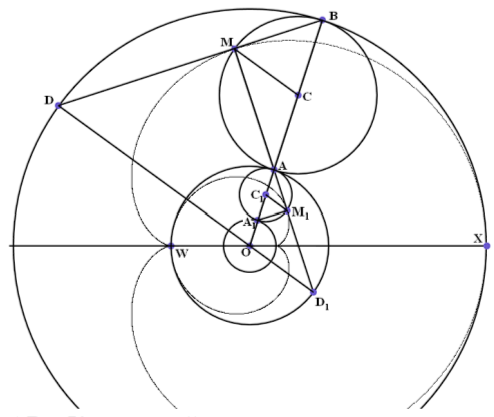
Доказательство. Дополним чертёж, использованный при доказательстве теоремы 1. Пусть, как и прежде, углы ХОВ и ВСМ равны u. Тогда, как мы уже знаем, угол XOD равен 2u, а отрезок АМ перпендикулярен хорде BD. Наконец, угол МСА равен π - u.

Продлим отрезок МА до второй точки пересечения с неподвижной окружностью. Обозначим её через D₁. Поскольку подвижная и неподвижная окружности равны, легко понять, что угол AOD₁ равен углу МСА, то есть равен π - u. Но и угол WOA также равен π - u.

Таким образом, нормаль к исходной кардиоиде отсекает от неподвижной окружности дугу AD₁. Концы этой дуги определяются углами π - u и 2*(π - u), если вести отсчёт от точки W.

Но согласно теореме 1 хорды, стягивающие такие дуги, являются касательными к некой кардиоиде.

Очевидно, что размеры этой кардиоиды в три раза меньше чем у исходной, поскольку исходная кардиоида огибается хордами окружности с радиусом в три раза большим, чем у неподвижной. Расположение малой кардиоиды, которая является эволютой исходной кардиоиды таково, что можно установить гомотетию относительно центра неподвижной окружности. Именно об этой гомотетии и говорится в условии доказываемой теоремы. Теорема доказана.

Естественно, что малая кардиоида может быть построена с помощью качения одной окружности по другой. Их радиус в три раза меньше, чем в исходной процедуре. Это обстоятельство показано на чертеже. Но следует иметь ввиду, что соответствие точек М и М₁ не является гомотетией. Кроме того, большая кардиоида возникает при качении большой окружности против часовой стрелки, а малая - при качении малой окружности по часовой стрелке.

Таким образом, на чертеже поймано только мгновение, после которого окружности с центрами С и С₁ покатятся в разные стороны. Тем не менее, наша конструкция позволяет доказать теорему.

5. УЛИТКИ ПАСКАЛЯ

Прежде всего, отметим, что улитки Паскаля названы не в честь знаменитого Блеза, а в честь его отца Этьена. Они, как и кардиоида, возникают в результате качения по неподвижной окружности равной ей подвижной окружности. Однако перо при этом не обязательно расположено на ободе. Оно может быть прикреплено к внутренней части спицы катящегося колеса, а также и к удлиненной спице, выходящей за пределы колеса.

Чтобы наглядно показать эти возможности опять ненадолго обратимся к процедуре построения циклоиды.

Циклоида одна, а удлинённых и укороченных циклоид бесконечно много. Каждая из них определяется одним параметром. Пусть радиус катящейся окружности равен r, а расстояние от центра этой окружности до пера равно r₁. Тогда на роль такого параметра естественно выбрать отношение k = r₁/r. Если k = 1, мы получаем обычную циклоиду.

Улитки Паскаля возникают аналогичным образом. Опять по закреплённой окружности катится равная ей окружность. Однако перо закреплено не обязательно на ободе, а на спице. Расстояние r1 от пера до центра катящейся окружности определяется тем же параметром k = r₁/r.

Теорема 7. Пусть точки В и D движутся по окружности радиуса 2r + r₁ с постоянными скоростями, причём скорость точки D в два раза больше скорости точки В. Точка М, которая отсекает постоянную часть хорды BD (ВМ = (r₁/(2r+r₁))BD) описывает одну из улиток Паскаля.

Однако в случае, когда k неравно 1, хорда BD уже не является касательной к соответствующей улитке Паскаля.

Доказательство. Чертёж, используемый при доказательстве данной теоремы, мало отличается от чертежа, используемого в доказательстве теоремы 1, как и рассуждения. Улитка Паскаля строится с помощью неподвижной окружности радиуса r с центром О и катящейся окружности радиуса r с центром С. Перо М удалено от С на расстояние r₁. Как и раньше ∠ ВОХ = ∠ ВСМ = ∠ ВОD = u. Равнобедренные треугольники ОВD и СВМ подобны, поскольку ∠ ВСМ = ∠ ВОD. Значит, у них равны и углы при основании, и точка М лежит на хорде ВD. Из подобия названных треугольников следует, что ВМ = (r₁/(2r+r₁))BD.

Кроме того, очевидно, что в случае, когда k неравно 1, и точка М не лежит на ободе катящейся окружности, отрезки АМ и ВD не перпендикулярны. Теорема доказана.

Мы не накладывали никаких ограничений на параметр k = r₁/r. В частности этот параметр может быть отрицательным. Пусть k - положительное число. Сравним две улитки, которые соответствуют двум значениям параметра: k и -k. На чертеже видно, что при втором значении рисуется точно такая же улитка Паскаля, но симметрично отражённая относительно вертикали.

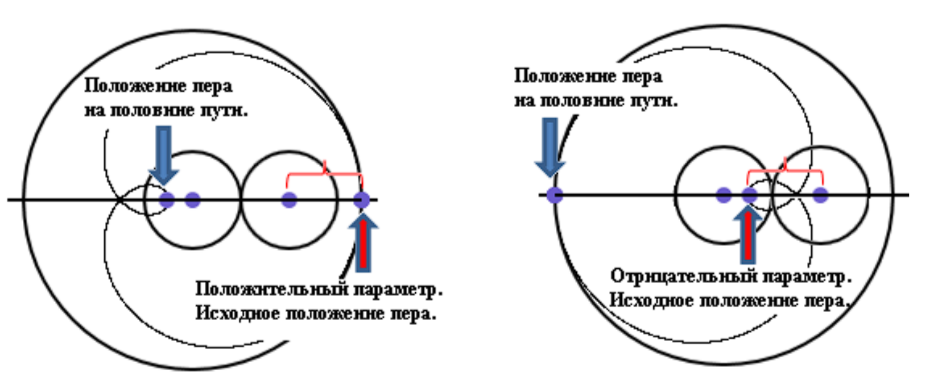
Таким образом, отрицательные значения не приводят к появлению новых по форме улиток Паскаля. Достаточно ограничиться только положительными значениями параметра k. Сразу отметим, что величина при изменении k от нуля доплюс бесконечности монотонно возрастает от нуля до 1.

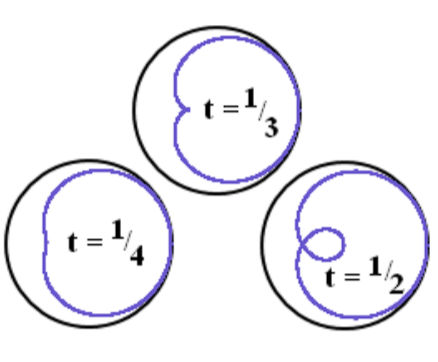
Теперь, используя теорему 7, можно описать процедуру построения улиток Паскаля без процедуры качения одного круга по другому. Рассмотрим окружность, на которой выделим исходную точку Х. Пусть из точки Х в одном направлении начинают равномерно двигаться точки В и D так, чтобы угловая скорость точки D была в два раза выше, чем у точки В. Тогда множество точек М хорды BD, определяемых условием ВМ = t*BD, образует улитку Паскаля.

Параметр t определяет улитку Паскаля однозначно. Кроме того, в отличие от процедуры качения, при которой улитки растут с ростом параметра k, с помощью параметра t, все наши кривые привязаны к одной исходной окружности и как бы вписаны в неё.

Теперь можно получить параметрические уравнения улитки Паскаля, определяемой параметром t. Точка В имеет координаты (г*cosu; г*sinu), а точка D - координаты (r*cos2u; г*sin2u). Координаты точки М вычисляются по формулам, которые и являются нужными уравнениями:

х_м = r*cos u + t*r*(cos 2u – cos u);
у_м = r*sin u + t*r*(sin 2u – sin u).

Теперь мы имеем возможность более подробно заняться изучением формы улиток Паскаля.

Прежде всего, констатируем факт, который можно установить экспериментально, используя компьютерную программу для построения улиток Паскаля с различными значениями параметра t.

pi = Math.Pi

x0 = 320

y0 = 220

r = 200

GraphicsWindow.DrawEllipse(x0-r,y0-r,2*r,2*r)

t = .5

For u = 0 To 2*pi Step pi/1000

xb = x0 + r* Math.Cos(u)

yb = y0 - r* Math.Sin(u)

xd = x0 + r* Math.Cos(2*u)

yd = y0 - r* Math.Sin(2*u)

xm = xb + t*(xd - xb)

ym = yb + t*(yd - yb)

GraphicsWindow.FillEllipse(xm-1,ym-1,2,2)

EndFor

Улитка Паскаля может иметь узловую точку (то есть точку самопересечения), а может её и не иметь. Своеобразной границей между двумя типами улиток является кардиоида, у которой узел вырождается в точку возврата.

Теперь мы можем описать улитки Паскаля как нечто единое с новой точки зрения, но для этого нам придётся стрелять из пушки по воробьям, поскольку мы для геометрических целей используем одно из важных понятий топологии - гомотопию.

Согласно [20] гомотопией называется семейство отображений h_t : X → Y, индексированных действительными числами t из единичного отрезка I, если непрерывно отображение H (x, t) = h_t (x) . Отображения h₀ и h₁ называются начальным и конечным отображениями гомотопии. Если пространство Х является подпространством пространства Y, то гомотопия осуществляет деформацию пространства Х в пространстве Y.

В нашем случае параметрические формулы улиток Паскаля осуществляют вложение окружности в плоскость, а вся совокупность таких вложений (то есть гомотопия) является деформацией окружности в плоскости. Начальным отображением гомотопии, как легко видеть, является недеформированная окружность, конечным окружность, уложенная в виде двойной петли. Таким образом, улитки Паскаля можно рассматривать как фазы деформации окружности в двойную петлю.

Поскольку речь идёт не о каких-либо абстрактных пространствах, а об объектах имеющих аналоги в быту, каждый может провести эксперимент, реализующий данную деформацию. При этом ему невольно придётся сдвинуться из сферы геометрии в область топологии, так как окружность утеряет свои правильные геометрические формы.

В отличие от несовершенного реального мира улитки Паскаля реализуют геометрически идеальный переход от одинарной окружности к двойной петле. Можно назвать этот переход каноническим.

При этом соответствующие точки деформируемой окружности движутся по прямым. Эти прямые нам уже хорошо известны и являются касательными к кардиоиде.

Следующим шагом в изучении улиток Паскаля является решение вопроса о местоположении узла. Как мы знаем, узел есть только у тех улиток, у которых перо находится за пределами катящейся окружности. Речь идёт о том случае, когда r₁>r или, что то же самое, когда k>1.

Когда же возникает узел? Он возникает в тот момент, когда перо, покинувшее начальное положение, вновь касается горизонтали, на которой лежит центр неподвижной окружности. Рассмотрим этот момент попристальней. В соответствующий момент центр катящейся окружности С удалён от точки касания U (эта точка как раз и является узлом) на расстояние r₁. Предположим, что точка А прошла за это время дугу, соответствующую центральному углу равному u. Тогда, как мы знаем, угол A₁CU (то есть угол между линией центров ОС и радиусом, на котором лежит перо) также равен u. Отсюда сразу следует, что ∠ UCA = ∠ UOA = π - u. Значит, треугольник UOC равнобедренный, то есть OU = UC = r₁. Итак, мы установили тот факт, что узел улитки Паскаля при k>1 смещён от центра неподвижной окружности на расстояние r₁ влево.

Хотя при k<1 не существует ни узла, ни точки возврата, назовем точку U, отстоящую от центра неподвижной окружности на расстояние r₁ влево, особой точкой для улитки Паскаля. В случае кардиоиды особая точка лежит на неподвижной окружности, в случае узла - вне его, и при его отсутствии - внутри.

Обоснованность подобного определения основана на следующем факте. Несмотря на то, что хорда BD не является касательной к улитке Паскаля, верно обобщение теоремы 3.

Теорема 8. Улитка Паскаля является огибающей окружностей, центры которых лежат на неподвижной окружности, а сами они проходят через особую точку данной кривой. Доказательство. Окружность с центром в точке А и радиусом АМ очевидным образом должна касаться улитки Паскаля. Однако вся проблема в том, проходят ли подобные окружности через одну точку, и если проходят, то, что это за точка. Легко догадаться, что окружности проходят через особую точку для улитки Паскаля.

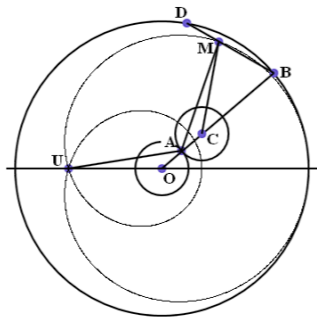
Доказать этот факт очень просто. Как мы знаем, МС = OU = п, ОА = ОС = r и, наконец, ∠ AOU = ∠ АСМ = π - u. Таким образом, треугольники АСМ и АОU равны, а, значит, АМ = AU, то есть окружность с центром в точке А соприкосновения подвижной и неподвижной окружностей, проходящая через соответствующую точку М улитки Паскаля проходит и через особую точку улитки U. Теорема доказана.

Продемонстрируем эту теорему с помощью двух компьютерных программ. Первая из них строит и семейство окружностей, и улитку Паскаля.

pi = Math.Pi

x0 = 320

y0 = 220

r = 30

k=3.5

r1 = k*r

GraphicsWindow.FillEllipse(x0-r1-5,y0-5,10,10)

For u = 0 To 2*pi Step pi/20

xa = x0+r* Math.Cos(u)

ya = y0-r* Math.Sin(u)

ra=Math.SquareRoot((x0-r1-xa)*(x0-r1-xa)+(y0-ya)*(y0-ya))

GraphicsWindow.DrawEllipse(xa-ra,ya-ra,2*ra,2*ra)

EndFor

For u=0 To 2*pi Step pi/1000

xc = x0 + 2*r* Math.Cos(u)

yc = y0 - 2*r* Math.Sin(u)

x = xc + r1* Math.Cos(2*u)

y = yc - r1* Math.Sin(2*u)

GraphicsWindow.FillEllipse(x-2,y-2,4,4)

EndFor

Вторая программа строит только семейства окружностей для трёх случаев: точка на границе, точка вне неподвижной окружности, точка внутри.

r = 40

x0 = 150

ug = 1

r1 = r

Окружности()

x0 = 320

ug = -1

r1 = r+20

Окружности()

x0 = 500

ug = 4

r1 = r - 20

Окружности()

Sub Окружности

xu = x0 + r1*Math.Cos(ug)

yu = y0 - r1*Math.Sin(ug)

For u=0 To 2* Math.Pi Step Math.Pi/20

xx = x0 + r*Math.Cos(u)

yy = y0 - r*Math.Sin(u)

rr = Math.SquareRoot((xu - xx)*(xu - xx)+(yu - yy)*(yu - yy))

GraphicsWindow.DrawEllipse(xx - rr,yy - rr,2*rr,2*rr) EndFor

EndSub

Поскольку к данному моменту уже становится очевидным то обстоятельство, что теория улиток Паскаля обобщает теоремы о кардиоиде, сделаем одно замечание. Оно связано с нашим, во всех отношениях несовременным, стилем изложения. Если кардиоида является одной из улиток Паскаля, нужно ли предварять разговор о более общем понятии разбором чего-то частного? Ответим на этот вопрос так - это дело вкуса и во многом связано с отношением автора к педагогическим проблемам. Они не менее важны, чем проблемы чисто математические. Теория же циклоидальных кривых, кроме всего прочего, является прекрасным мостом, связывающим элементарную геометрию с геометрией дифференциальной.

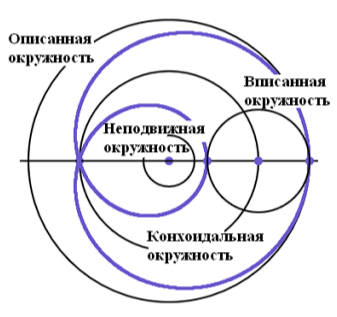
По этой причине продолжим наш экскурс и рассмотрим улитку Паскаля как подэру и конхоиду. Но сначала дадим названия некоторым окружностям, связанным с улитками Паскаля, а также расширим наш терминологический запас. Это позволит нам более компактно сформулировать последующие теоремы.

Если улитка Паскаля будет построена известным нам способом при фиксированных параметрах r и r₁, то окружность радиуса 2r*r₁ концентричную неподвижной окружности, назовём описанной вокруг улитки Паскаля (об этом мы уже говорили выше). Окружность, концентричную неподвижной окружности и имеющую радиус r₁ назовём конхоидальной. О третьей окружности придётся говорить подробнее. Мы выбрали определённый способ построения, отправляясь от горизонтальной прямой (более корректно было бы называть эту прямую осью симметрии улитки Паскаля). Начальная точка улитки Паскаля соответствует углу, равному нулю. Точку, соответствует углу л, назовём срединной точкой улитки Паскаля. Окружность, построенную как на диаметре на отрезке, соединяющем начальную и срединную точки улитки Паскаля, назовём вписанной в улитку. Отрезок, проходящий через особую точку и соединяющий две точки на улитке Паскаля, назовём диаметром этой кривой.

Теорема 9. Пусть точка М на улитке Паскаля определяется углом u, а точка М₁ - углом u+π. Тогда отрезок ММ₁ является диаметром улитки и наклонён к горизонтали под тем же углом u.

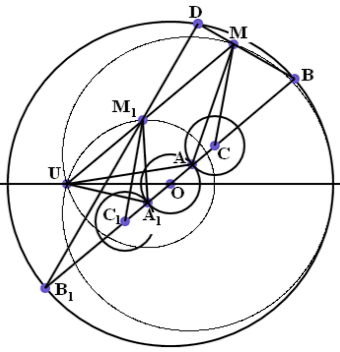
Доказательство. При доказательстве теоремы 7 мы использовали тот факт, что треугольники АСМ и AOU равны. По этой причине равны и их высоты опущенные на стороны АО и АС (эти стороны лежат на одной прямой ОС). Таким образом, точки U и М удалены от прямой ОС на одинаковое расстояние. Значит, прямая UM параллельна прямой ОС. Аналогичное рассуждение показывает, что равны и треугольники А₁С₁М₁ и A₁OU. Из чего следует, что прямая UM₁ тоже параллельна прямой ОС. Точки U, М и М₁ лежат на одной прямой, наклонённой под углом u. Теорема доказана.

Теорема 10. Улитка Паскаля является конхоидой относительно конхоидальной окружности и своей особой точки с расстоянием r.

Доказательство. Мы уже доказали, что параллельны пары прямых СМ и СМ₁, а также СС₁ и ММ₁. Прямая OD также параллельна СМ. Таким образом, четырёхугольник СС₁М₁М является параллелограммом. Прямая OD проходит через середину стороны СС₁ и параллельно сторонам СМ и С₁М₁. Тем самым, точка К её пересечения со стороной ММ₁ является серединой этой стороны. Кроме того, ОК = СМ = r₁ и С₁О = М₁К = КМ = r. Это значит, что точка К лежит на конхоидальной окружности, а улитка Паскаля является конхоидой этой сти относительно точки U с расстоянием r. Теорема доказана.

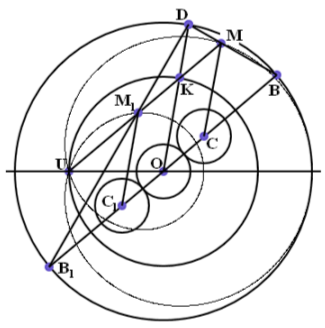
Между прочим, отметим, что, как и в случае кардиоиды, точки D и D₁ совпадают, но взаимно перпендикулярные хорды описанной окружности BD и B₁D уже не являются касательными к улитке Паскаля.

Теорема 11. Улитка Паскаля является подэрой относительно вписанной окружности и особой точки.

Доказательство. Построим вписанную окружность и проведём её радиус WP, наклонённый под углом u к горизонтали. Будем иметь ввиду, что прямые UM, ОВ и WP параллельны.

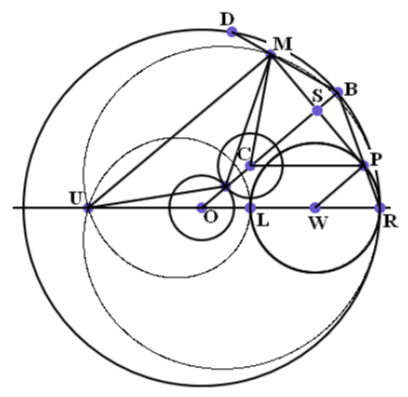
Поскольку по построению СО = WP = 2r, четырёхугольник COWP является параллелограммом. Значит, СР = OW = OR - WR = 2r + r₁ - 2r = r₁. Соединим точки М и P. Треугольники МСS и PCS равны, поскольку у них есть общая сторона CS, CM = CP = r₁ и ∠ MCS = ∠ PCS = u. Из этого следует, что ∠ MSC = ∠ PSC = 90°, то есть отрезки MP и ОВ перпендикулярны. Но тогда отрезок MP перпендикулярен и WP, то есть прямая MP касается вписанной окружности. Прямая MP перпендикулярна и к отрезку UM, то есть точка M является основанием перпендикуляра, опущенного на касательную к вписанной окружности из особой точки. Теорема доказана.

Уравнение улитки Паскаля в полярных координатах выводится с помощью теоремы 10, абсолютно аналогично случаю кардиоиды. Естественно, за полюс полярной системы координат в этом случае мы принимаем особую точку улитки Паскаля. Не вдаваясь в подробности, получаем, что уравнение улитки Паскаля в полярных координатах имеет вид ρ = 2·r·(k + cosu), где в наших привычных обозначениях k = r₁/r.

И снова по аналогии с кардиоидой без введения каких-либо новых соображений, переходя от полярных координат к декартовым, получаем, что улитка Паскаля является алгебраической кривой четвёртого порядка.

6. ЭПИЦИКЛОИДЫ

Улитки Паскаля являются частным видом, так называемых циклоидальные кривых. Циклоидальные кривые образуются при качении без скольжения одного круга по другому, в том числе и по внутреннему ободу. При этом круги могут иметь разный диаметр. Если вычерчивающее перо находится на ободе катящегося круга, то в случае внешнего соприкосновения кругов кривая называется эпициклоидой, а в случае внутреннего соприкосновения - гипоциклоидой. По аналогии с циклоидой могут рассматриваться удлинённые и укороченные эпициклоиды и гипоциклоиды. Они, в свою очередь называются трохоидами. При этом используются термины - эпитрохоиды и гипотрохоиды.

Кардиоида является эпициклоидой (перо на ободе) в случае, когда неподвижная и катящаяся окружности равны. Улитки Паскаля также были определены нами, как эпитрохоиды, когда неподвижная и катящаяся окружности равны. Неудивительно, что теория циклоидальных кривых строится во многом по аналогии с теорией улиток Паскаля.

Начнём с эпициклоид (ещё раз подчеркнём, что при их вычерчивании перо находится на ободе катящегося круга). Важнейшим параметром, определяющим их форму, является отношение радиусов неподвижного и катящегося круга. Обозначим эти радиусы как r₀ и r₁, а отношение r₁/r₀ - через k₁. Это число будет принимать у нас любые положительные действительные значения. Таким образом, каждая из эпициклоид не только соответствует некому числу, но и, как мы увидим в дальнейшем, как бы его изображает.

Форма эпициклоид в общих чертах может быть установлена уже на уровне предварительного размышления, а для некоторых значений параметра k₁ легко её усмотреть во всех деталях. Например, пусть k₁ = 1/n, где n - натуральное число, большее, чем единица. Тогда катящееся колесо обойдёт неподвижное n раз. При этом перо n раз коснётся неподвижной окружности. Кривая, соединяющая точки двух последовательных касаний, имеет форму близкую к арке циклоиды. Итак, в рассматриваемом случае на неподвижную окружность опираются n равных арок. При этом вершина арки удалена от неподвижной окружности на расстояние 2r₀/n.

В более сложных случаях, пожалуй, не лишне дополнить размышление непосредственным созерцанием кривой. В книгах [21] и [22], изданных в начале шестидесятых годов прошлого века есть разделы, посвящённые замечательным кривым. В частности там рассказывается о приёмах построения различных кривых на листе бумаги. При этом от читателя, пожелавшего воспользоваться рекомендациями авторов, требуются определённые чертёжные навыки и, что особенно важно, немалая толика терпения. Не обсуждая плюсы и минусы современных технологий, предоставляемых компьютером, отметим, что написав одну программу можно за короткое время увидеть на экране сотни кривых.

В тексте программы, основанной на имитации качения круга по кругу и предназначенной для построения эпициклоид, следует менять только значения натуральных чисел m и n, задающих параметр k₁ в виде дроби m/n.

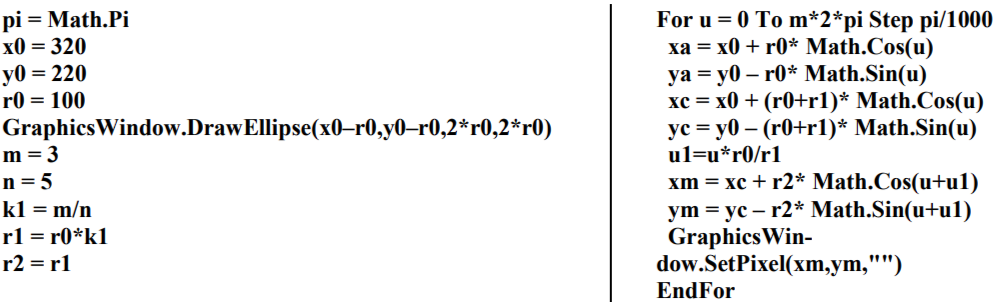
Продемонстрируем несколько эпициклоид, сопроводив их изображения комментариями. Но предварительно докажем теорему, которая является прямым обобщением теоремы 1. Она, кроме всего прочего, поможет лучше понять нашу программу.

Теорема 12. Пусть точки В и D движутся по окружности радиуса r₀+2r₁ с постоянными скоростями, причём скорость точки D в 1 + 1/k₁ раз больше скорости точки В. Точка М, определяемая условием , описывает эпициклоиду, а любая хорда BD является касательной к этой эпициклоиде.

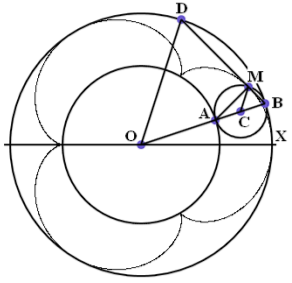
Доказательство. Эпициклоида строится с помощью неподвижной окружности радиуса r₀ с центром О и катящейся окружности радиуса r₁ с центром С (r₁ = k₁*r₀). Пусть ∠ ВОХ = u. Тогда длина дуги неподвижной окружности, по которой прокатилась подвижная окружность, равна r₀*u. Такова же и длина дуги подвижной окружности, пришедшей в соприкосновение с неподвижной. Центральный угол, опирающийся на эту дугу, равен u₁ = u*r₀/r₁ Выберем точку D так, чтобы ∠ BОD = u₁.

Итак, соприкоснувшиеся при качении дуги обеих окружностей имеют длину r₀*u. Из исходного положения Х перо переместилось в точку М. При этом горизонтальная линия ОХ перешла в линию ОВ, а перо же за счёт качения отклонилось от этой линии на угол u₁, то есть ∠ ВСМ = u₁. Треугольники ОBD и СВМ являются равнобедренными и имеют углы при вершинах равные u₁. Значит у них равны и углы при основании, то есть ∠ СВМ = ∠ ОBD = π-u₁/2. Из этого следует, что точка М лежит на хорде BD. Из подобия названных треугольников следует, что ВМ = k₁/(1+2k₁)*BD.

Далее ∠ АМВ является прямым, так как вписан в катящуюся окружность и опирается на её диаметр. Таким образом, треугольник МАВ является прямоугольным, то есть хорда BD перпендикулярна отрезку АМ, исходящему из неподвижный в данный момент точки А. Это означает, что хорда BD является касательной к этой эпициклоиде в точке М. Теорема доказана.

Теперь вернёмся к изучению внешнего вида эпициклоид и их сопоставлению с положительными действительными числами. При этом будет уместно вспомнить о существовании такого древнего феномена, как узелковая письменность. В наше время узелковая письменность продолжает привлекать внимание, возможно, в несколько экзотической форме. Например, можно сослаться на эзотерический язык программирования Quipu, созданный на основе узелковой письменности Инков. Для нас важно, что узелки позволяют очень естественно фиксировать натуральные числа. Если кроме верёвки использовать стержень, то числу n будет соответствовать узел, n раз обёрнутый вокруг стержня.

Рассмотрим эпициклоиду, соответствующую k₁ = n. Для того чтобы перо, изначально максимально удалённое от неподвижной окружности, подвижная окружность должна сделать полный оборот. При этом она n раз обогнёт неподвижную окружность, то есть опишет узелковую петлю, соответствующую числу n. При этом перо только однажды коснётся неподвижной окружности. Можно сказать, что вокруг неподвижной окружности n раз обогнётся одна единственная арка циклоиды, основания которой сойдутся в одной точке. В частности кардиоида, соответствующая числу 1, представляет собой одинарную арку.

 

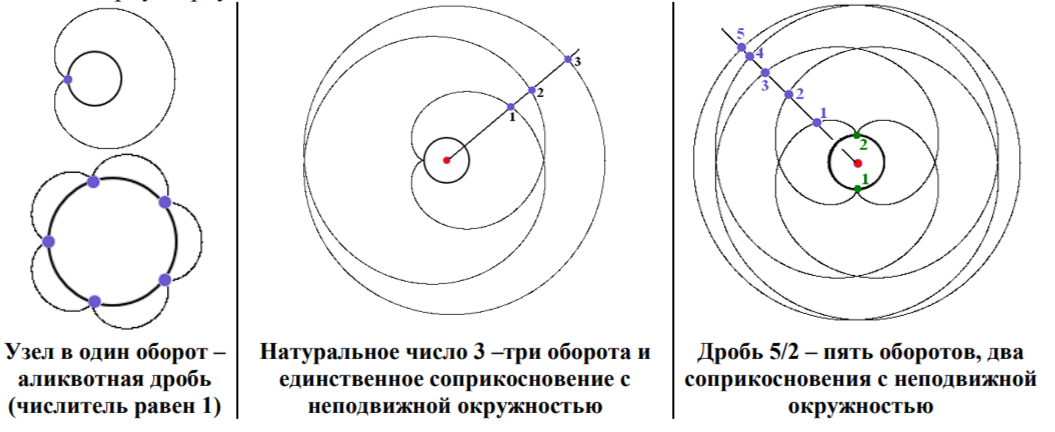
Наши уравнения используют два исходных параметра: r₀ и k₁. Убедимся, что с их помощью легко построить любые эпициклоиды, связанные с общей неподвижной окружностью, не используя имитацию процесса качения как раньше. Применим уравнения в программе построения двух эпициклоид.

Предварительно отметим, что получить замкнутую кривую удастся только при рациональном значении k₁=m/n. При этом значение параметра u должно меняться от нуля до 2π*m.

Теорема 13. Пусть точки В и D движутся по окружности радиуса r с постоянными скоростями, причём скорость точки D в q раз больше скорости точки В. Точка М, определяемая условием ВМ = 1/(1+q)*BD, описывает эпициклоиду, а любая хорда BD является касательной к этой эпициклоиде.

Эта теорема обобщает теорему 1, относящуюся к кардиоиде, на случай любых эпициклоид. Проиллюстрируем теорему с помощью программы.

Теперь обобщим теорему 6.

Теорема 14. Эволютой эпициклоиды является также эпициклоида, гомотетичная исходной относительно центра неподвижной окружности с коэффициентом, равным -(1/1+2k₁), где k₁=r₁/r₀.

Доказательство. Будем использовать привычные уже обозначения. Например, точка А – точка касания неподвижной и подвижной окружностей, точкам М лежит на эпициклоиде, ∠ BOX = u, ∠ XOD = q*u, где q=1+1/k₁. К данному моменту мы знаем, что отрезки MC и OD параллельны и что MA - нормаль к эпициклоиде.

Используем в своих рассуждениях следующий факт: две соприкасающиеся окружности с радиусами r₀ и r₁ гомотетичны относительно точки касания. Это следует из подобия двух прямоугольных треугольников АМВ и АD₁Р. Кроме того, ясно, что коэффициент гомотетии равен -(r₁/r₀)=-k₁.

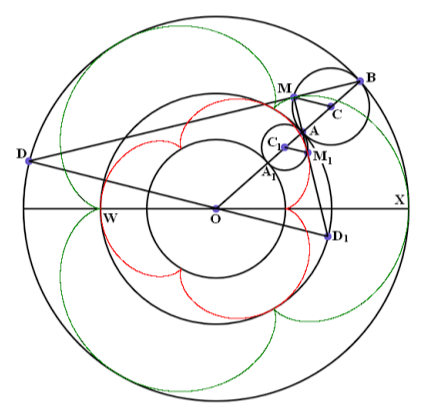
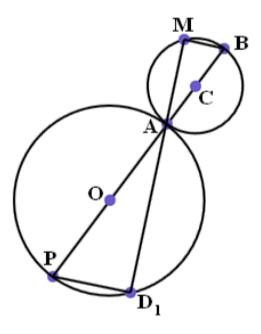
Продолжим нормаль МА до пересечения с неподвижной окружностью во второй точке D1. Тогда, используя сказанное выше, мы получим, что отрезок ОD₁ параллелен отрезку СМ, а, значит, и отрезку ОD. Таким образом, точки D, О и D₁ лежат на одной прямой. Из этого следует, что при кинематической интерпретации построения эпициклоиды (точка В движется с единичной скоростью, точка D движется со скоростью q) точки D и D₁ имеют одинаковую угловую скорость. То же самое можно сказать и об угловых
скоростях точек А и В.

Это означает, что точка М₁ на хорде АD₁ (AM₁=1/(1+q)*AD₁) по теореме 13 вычерчивает эпициклоиду, вписанную в неподвижную окружность. Очевидно, что коэффициент подобия малой и большой эпициклоид равен отношению

Взаимное расположение этих эпициклоид, можно установить с помощью следующих соображений. До этого мы рассматривали процесс движения точек В и D, начиная с момента их совмещения. Теперь же мы установили факт движения точек с нужными угловыми скоростями, но в момент, когда они находятся на некотором расстоянии друг от друга. Никакой проблемы здесь нет. Поскольку точки движутся по кругу в одном направлении с разными скоростями, более быстрая точка D₁ догонит точку А. С этого момента мы попадаем в знакомую нам ситуацию.

Вопрос в том, когда точки А и D₁ совместятся. Решение его достаточно просто. Соответствующие точки совместятся, когда эпициклоида коснётся неподвижной окружности, то есть в верхней точке арки. Но поскольку точка М₁, вычерчивающая малую эпициклоиду гомотетична точке М относительно точки А, Точка М₁ попадёт на неподвижную окружность одновременно с точкой М, вычерчивающей исходную эпициклоиду, то есть в опорной точке арки этой кривой. Таким образом, вершины арок эволюты совпадают с точками излома исходной эпициклоиды. Теорема доказана.

7. ЭПИТРОХОИДЫ

В отношении к эпициклоидам эпитрохоиды занимают то же место, которое улитки Паскаля занимают в отношении кардиоиды.

Теорема 15. Пусть точки В и D движутся по окружности радиуса r₀ + r₁ +r₂ с постоянными скоростями (r₁ = k₁*r₀, r₂ = k₂*r₁). Если скорость точки D в q=1+1/k₁ раз больше скорости точки В, то точка М, которая отсекает r постоянную часть хорды BD (ВМ = r₂/(r₀ + r₁ +r₂)*BD) описывает эпитрохоиду.

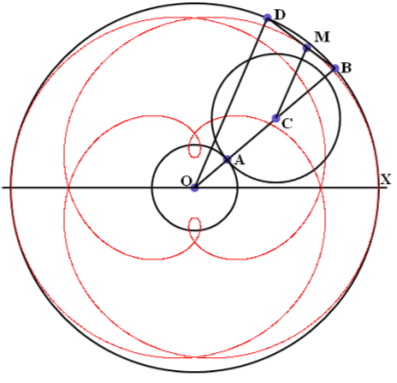
Доказательство. Будем использовать неподвижную окружность с радиусом r₀ и подвижную окружность с радиусом r₁, причём перо отстоит от её центра на расстояние r₂. Очевидно, что возникающая кривая вписана в окружность радиуса r = r₀ + r₁ + r₂, а сам процесс качения такой же как и при построении эпициклоиды.

Отличие только в том, отрезки СВ, СМ и OD либо длиннее, либо короче, чем радиус подвижной окружности. Однако подобие треугольников BOD и ВСМ имеет место и в этом случае, что и доказывает теорему.

Величина r₂/r₀ + r₁ + r₂ при изменении r₂ от нуля до бесконечности меняется от нуля до единицы.

Из этого следует

Теорема 16. Пусть точки В и D движутся по окружности с неравными постоянными скоростями. Тогда каждая из точек М, делящих хорду BD в постоянном отношении описывает свою эпитрохоиду.

Пусть скорости точек В и D и относятся как натуральные числа m и n. Тогда в своих крайних положениях на хорде BD точка М на конце В делает m оборотов, а на конце D - n оборотов. По аналогии с рассуждениями, проведёнными в отношении улиток Паскаля, можно прийти к заключению, что соответствующие эпитрохоиды реализуют геометрически идеальный переход от m-кратной петли к n-кратной петле. Продемонстрируем это обстоятельство с помощью программы.

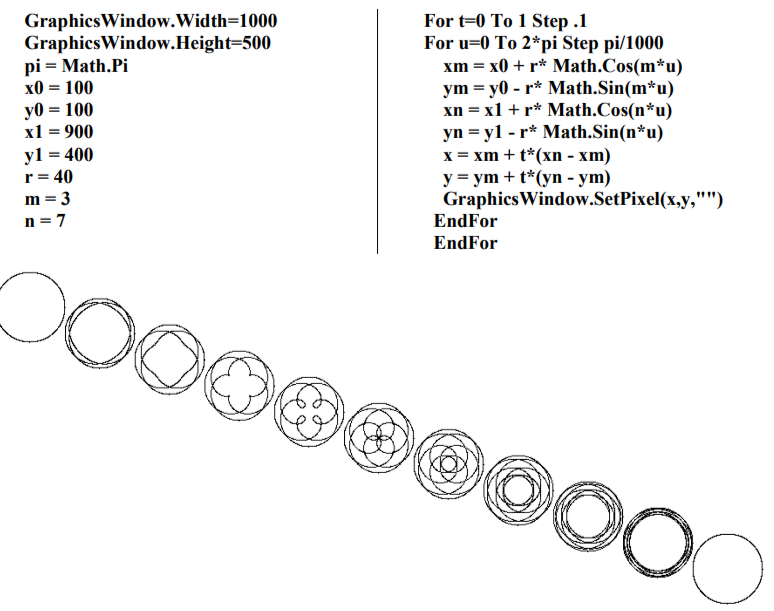
Продолжение данной статьи будет начато с изучения гипоциклоид, среди которых важнейшее значение для нас будет играть кривая Штейнера. Как известно, эта кривая является важным объектом в геометрии треугольника - она является огибающей прямых Симсона. С её помощью и будет строиться группа преобразований, элементы которой позволяют переводить произвольный треугольник в любой другой.

1. В.И. Арнольд. Что такое математика? М., Изд. МЦНМО. 2004.
2. В.И. Арнольд. Экспериментальная математика? М., Фазис. 2005.
3. В.И. Ленин. Материализм и эмпириокритицизм. М., Госполитиздат. 1950.
4. Ф.Клейн. Лекции об икосаэдре и решении уравнений пятой степени. М., Наука, 1989.
5. А.Н. Колмогоров. Математика в еѐ историческом развитии. М., Изд. ЛКИ. 2007.
6. Г.С. М. Кокстер. Введение в геометрию. М., Наука, 1966.
7. В.И. Арнольд. Астроидальная геометрия гипоциклоид и гессианова топология гипербо­лических многочленов. М., Изд. МЦНМО. 2001.
8. Ф. Клейн. Высшая геометрия. М. – Л. Гос. объединенное научно-техническое изд. 1939.
9. История отечественной математики. Том 3. Киев, Наукова думка. 1968.
10. С. И. Зетель. Новая геометрия треугольника. М., Учпедгиз. 1962.
11. Математическая энциклопедия. Том 5. М., Советская энциклопедия. 1985.
12. И.М. Яглом. Геометрические преобразования. Том 1. М., Гос. изд. технико­теоретической лит. 1955.
13. И.М. Яглом, В. Г. Ашкинузе. Идеи и методы аффинной и проективной геометрии. Часть М., Гос. уч.-пед. изд. Министерства просвещения РСФСР. 1962.
14. В.Ю. Овсиенко, С. Л. Табачников. Проективная дифференциальная геометрия. М., Изд. МЦНМО. 2008.
15. И.М. Яглом. Геометрические преобразования. Том 2. М., Гос. изд. технико­теоретической лит. 1956.
16. Б.А. Розенфельд. Аполлоний Пергский. М., Изд. МЦНМО. 2004.
17. В.В. Прасолов. Геометрия Лобачевского. М., Изд. МЦНМО. 2004.
18. Математика XIX века: Геометрия. Теория аналитических функций. М., Наука, 1981.
19. А.А. Савѐлов. Плоские кривые: Систематика, свойства, применения. М., Книжный дом «Либроком¬, 2010.
20. Ху Сы-Цзян. Теория гомотопий. М., Едиториал УРСС, 2004.
21. М.Я. Выготский. Справочник по высшей математике. М., Гос. изд. физ.-мат. лит. 1962.
22. А.П. Доморяд. Математические игры и развлечения. М., Гос. изд. физ.-мат. лит. 1961.
23. Ф. Клейн. Лекции о развитии математики в XIX столетии. Т. 1. М.; Наука. 1989.
24. Хрестоматия по истории математики. Арифметика и алгебра. Теория чисел. Геометрия. М., Просвещение, 1976.
25. В. Ф. Каган. Лобачевский. М. – Л., Изд. АН СССР, 1944.
26. Об основаниях геометрии. Сборник классических работ по геометрии Лобачевского и развитию его идей. М., Гос. изд. технико-теоретической литературы, 1956.
27. С. В. Бахвалов, Л. И. Бабушкин, В. П. Иваницкая. Аналитическая геометрия. М., Учпед­гиз, 1962.
28. М.А. Акивис, Б. А. Розенфельд. Эли Картан. М., Изд. МЦНМО. 2007.
29. Ж. Дьедонне. Линейная алгебра и элементарная геометрия. М., Наука, 1972.