Эрландская программа Клейна и геометрия треугольник (часть вторая)

В данной статье сопоставляются геометрия треугольника и Эрлангенская программа Ф. Клейна, в результате чего выявляется ошибочность распространённой трактовки планиметрии Евклида как учения об инвариантах группы движений плоскости. Автор рассматривает один из возможных способов устранения данной ошибки с помощью построения иной группы преобразований. В статье излагаются необходимые сведения, относящиеся к геометрии циклоидальных кривых и геометрии треугольника. Большой объём статьи потребовал её разбиения на две части.

8. ГИПОЦИКЛОИДЫ

Гипоциклоиды возникают при качении подвижной окружности по внутреннему ободу неподвижной окружности. При этом перо находится непосредственно на ободе подвижной окружности.

При переходе от изучения эпициклоид к изучению гипоциклоид проявляется одно интересное обстоятельство. Процесс порождения эпициклоид и гипоциклоид определяется нами как результат некой кинематической процедуры, которая может быть воспроизведена в реальном мире. Как физическое действо он предстаёт перед наблюдателем в предельно конкретном виде. При этом вычерчивание эпициклоиды обнаруживает значительное сходство с вычерчиванием гипоциклоиды - и там, и там происходит качение кругов друг по другу. Однако и имеющиеся отличия весьма значительны. В частности это проявляется в форме, которую имеют эпициклоиды и гипоциклоиды.

Но, как мы скоро увидим, математическое описание и тех, и других кривых сходно. Для получения гипоциклоид достаточно допустить использование отрицательных параметров. В результате появляется возможность детального анализа двух процессов, отличающихся на физическом уровне. При этом мы можем сделать упор на созерцание геометрических образов. Целью же нашего созерцания является объяснение тождественности аналитического описания двух различных процессов. По крайней мере, с педагогической точки зрения такие размышления могут быть весьма полезными.

По этому поводу следует дать небольшой исторический комментарий. Подобно тому, как неевклидова геометрия, можно сказать, самочинно вошла в математику, не обращая ни малейшего внимания на предшествующие её появлению взгляды и теории, иррациональные, отрицательные и мнимые числа заставили признать себя, хотя их выталкивало из математики чуть ли не всё учёное сообщество. Иррациональные числа принесли с собой кризис пифагорейской философии, но их появление привело к созданию теории Евдокса, повторённой только в девятнадцатом веке. Что же касается отрицательных и мнимых чисел, то они окончательно получили гражданство в математике в том же веке.

И хотя Даламбер и Лазарь Карно отрицали объективное существование отрицательных величин [1], формулы Кардано и Эйлера своей незыблемой эффективностью заставляли расширить понятие числа, признав недавних изгоев полноправными числами.

Особый интерес представляет использование отрицательных и мнимых чисел в геометрии. Штейнер их избегал, как только мог, что в целом ему навредило, а Ламберт сумел предсказать осуществление новой геометрии на сфере мнимого радиуса. Однако до работ Бельтрами никому и в голову не могло прийти, что такая сфера может существовать в трёхмерном пространстве в виде реальной поверхности. Именно по этой причине хотелось бы обратить внимание на то, что элементарная по своим методам теория циклоидальных кривых позволяет проследить один из вариантов «самовольного» вхождения отрицательных чисел в геометрию, приводящий к единой теории.

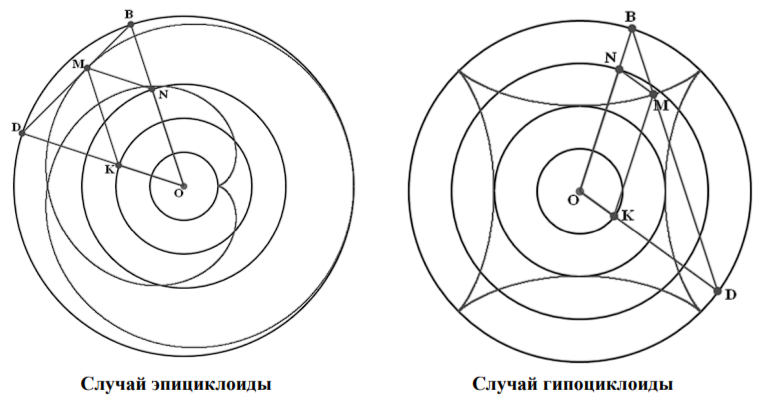
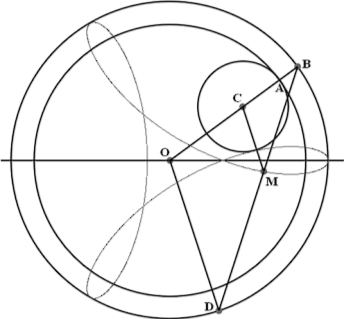
Приступая к изучению гипоциклоид, мы по мере возможности сохраним обозначения из первой части статьи. Прежде всего, речь идёт о том, что r₀ - радиус неподвижной окружности и r₁ - радиус подвижной окружности, где r₁ = k₁*r₀. Кроме того, мы сохраним на чертежах обозначение важных точек: О - центр неподвижной окружности, С - подвижной, А - точка их соприкосновения.

Для того, чтобы сходства и различия в построении эпициклоид и гипоциклоид проявились особенно наглядно расположим рядом чертежи, связанные с построением кардиоиды и кривой Штейнера (k₁=1/3).

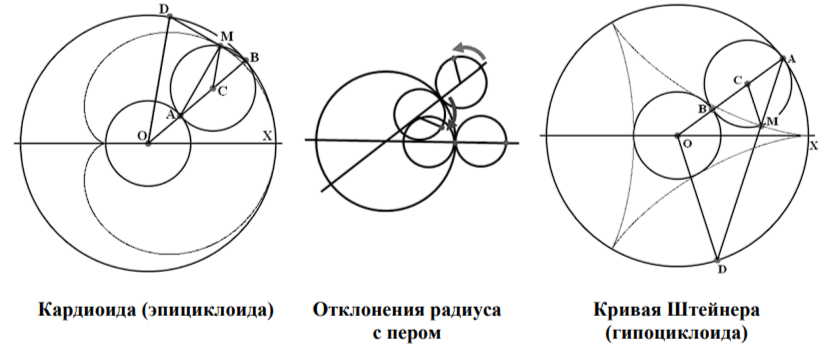
На чертеже показано главное различие, возникающее при построении эпициклоид и гипоциклоид. При построении эпициклоиды радиус подвижной окружности с пером вращается в том же направлении, что и линия центров подвижной и неподвижной окружностей. При построении гипоциклоиды радиус подвижной окружности с пером вращается в противоположном направлении от направления вращения линии центров подвижной и неподвижной окружностей. Тут мы видим первую причину появления знака минус. Действительно, важнейшая интерпретация положительных и отрицательных величин основывается на использование противоположных направлений. Мы ещё вернёмся к этому вопросу, а пока докажем очередную теорему.

Теорема 17. Пусть точка A движется по неподвижной окружности с постоянной единичной угловой скоростью, а точка D в противоположном направлении со скоростью 1-1/k₁, тогда точка М (АМ = k₁*АD) вычерчивает гипоциклоиду.

Доказательство. Несмотря на то, что почти всё доказательство является повторением доказательства аналогичной теоремы об эпициклоидах, приведём его полностью. Гипоциклоида строится с помощью неподвижной окружности радиуса r₀ с центром О и подвижной окружности радиуса r₁ с центром С (r₁ = k₁*r₀). При этом качение осуществляется по внутренней стороне обода.

Пусть линия центров ОС, на которой лежит точка А, движется против часовой стрелки и ∠ АОХ = u. Длина дуги неподвижной окружности, по которой прокатилась подвижная окружность, равна r₀*u. Такова же и длина дуги подвижной окружности, пришедшей в соприкосновение с неподвижной. Центральный угол, опирающийся на эту дугу, равен u₁ = u*r₀/r₁ = u/k₁

Выберем точку D так, чтобы ∠ AОD = u - u₁. Пусть из исходного положения Х перо переместится в точку М. Мы уже установили, что радиус СМ вращается по часовой стрелке. При этом горизонтальная линия ОХ переходит в линию ОА, а перо же за счёт качения отклонилось от этой линии на угол u₁, то есть ∠ АСМ = u - u₁. Треугольники ОAD и СВМ являются равнобедренными и имеют углы при вершинах равные u₁. Значит у них равны и углы при основании, то есть ∠ САМ = ∠ ОAD = (π-u₁)/2. Из этого следует, что точка М лежит на хорде AD. Из подобия названных треугольников следует, что АМ = r₁/r₀*AD = k₁*AD. Теорема доказана.

Как и в случае эпициклоид, мы можем получить параметрические уравнения гипоциклоид. Точка А имеет координаты (r₀*cos u; r₀*sin u), а точка D - координаты (r₀*cos(1-1/k₁)u; r₀*sin(1-1/k₁)u). Координаты точки М вычисляются по формулам, которые и являются нужными уравнениями:

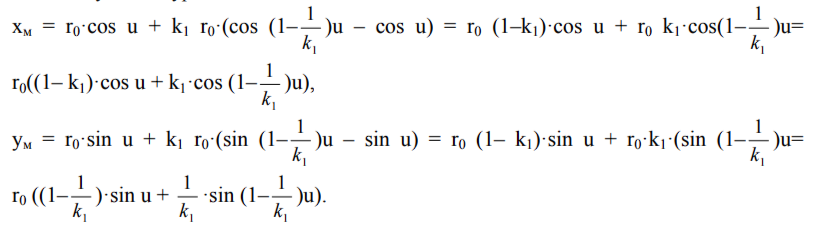
Окончательно получаем:

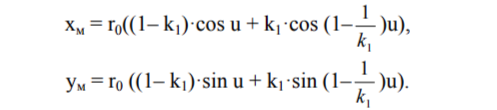
Как и для эпициклоид, наши уравнения, используя два исходных параметра r₀ и k₁, позволяют построить любые гипоциклоиды, связанные с общей для них неподвижной окружностью. При этом нет необходимости проводить имитацию процесса качения.

Применим уравнения в программе построения гипоциклоиды. Для получения замкнутой кривой следует использовать рациональные значения параметра k₁ = m/n. При этом значение угла u должно меняться от нуля до 2π*m.

Теперь заменим параметр k₁ на отношение скоростей точек, движущихся по этой окружности. Обозначим это число, как и раньше, через q (q = 1-1/k₁). Из этого равенства получаем, что k₁ = -(1/(q-1)) = 1/(1-q). Это то число, которое определяет положение точки М на хорде.

Теорема 18. Пусть точки А и D движутся по окружности радиуса r₀ с постоянными угловыми скоростями в разные стороны, причём модуль скорости точки D в q раз больше скорости точки А. Точка М, определяемая условием АМ = 1/(1-q)*AD, описывает гипоциклоиду, а любая хорда AD является нормалью к этой гипоциклоиде.

Теорема эта практически является переформулированной теоремой 17. Если же её сравнить с аналогичной теоремой 13, связанной с эпициклоидами, мы видим ещё одно существенное различие между эпициклоидами и гипоциклоидами. Оно, конечно же, проявилось уже в момент сопоставления чертежей, связанных с построением кардиоиды и кривой Штейнера.

И там, и там движутся две точки, соединяющая их хорда делится в постоянном отношении и точка деления вычерчивает циклоидальную кривую. Но в случае эпициклоид точки В и D движутся по окружности радиуса r₀ + 2r₁, а хорда BD является касательной к соответствующей кривой. В то же время в случае гипоциклоид точки А и D движутся по неподвижной окружности радиуса r₀, а хорда AD является нормалью к соответствующей кривой, поскольку проходит через неподвижную точку А соприкосновения неподвижной и подвижной окружностей. Точки А и В при этом меняются ролями.

Для нас в дальнейшем будет особенно важен вопрос, состоящий в нахождении и описании семейств прямых, являющихся огибающими гипоциклоид. Для эпициклоид он уже решён. В случае же гипоциклоид роль касательных играют нормали. По этой причине необходимо продолжить исследование этих кривых.

В процессе исследования мы будем использовать кинематические методы. Прежде всего вспомним кинематическую теорему Эйлера: произвольное мгновенное движение твёрдого тела в любой момент времени может быть представлено как сумма двух мгновенных движений: одного мгновенно-поступательного и одного мгновенно-вращательного [2].

Пусть на плоскости выделено семейство параллельных прямых. Зададим центр вращения О и начнём вращать плоскость с постоянной угловой скоростью. Каждая прямая из выделенного семейства будет двигаться как аналог твёрдого тела. Чистое вращение будет осуществлять только та прямая, которая проходит через центр вращения. Остальные прямые семейства будут по теореме Эйлера сочетать в своём перемещении и вращательное, и поступательное движение. Однако поступательное движение не изменяет направления прямой. По этой причине на это направление влияет только вращательная составляющая. И с этой точки зрения можно рассматривать движение всех прямых семейства как вращение с постоянной угловой скоростью. Поступательной составляющей мы просто будем пренебрегать.

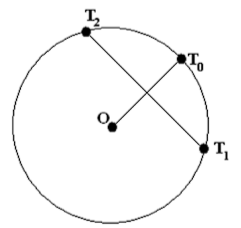
Исходя из этого соображения, можно утверждать, что если одна прямая вращается (в нашем понимании) с постоянной угловой скоростью, а вторая движется так, что всегда образует с первой прямой постоянный угол, то она также вращается с той же угловой скоростью. В частности это имеет место для перпендикулярных прямых.

Рассмотрим окружность с центром О, по которой движутся две точки Т₁ и Т₂ с угловыми скоростями 1 и q (скорость q может быть и отрицательной). В момент старта точки совмещены. Если точка Т₁ замела в процессе движения дугу, имеющую угловую меру u, то точка Т₂ заметёт дугу, имеющую угловую меру q^u. Опустим из центра окружности О перпендикуляр на хорду Т₁Т₂ и продлим его до пересечения с окружностью в точке Т₀. Радиус ОТ0 делит дугу Т₁Т₂ пополам, следовательно, точка Т₀ замела в процессе движения дугу, имеющую угловую меру (1+q)/2*u. Таким образом, её угловая скорость равна среднему арифметическому скоростей точек Т₁ и Т₂. Такова же скорость вращения радиуса ОТ₀.

Наши предыдущие рассуждения позволяют сделать заключение, что перпендикулярная этому радиусу хорда Т₁Т₂ вращается с той же угловой скоростью.

Теперь мы можем выяснить, как ведут себя касательные к гипоциклоидам, а затем по аналогии описать поведение нормалей к эпициклоидам. Это дополнение в чём-то прояснит теорему об эволютах к эпициклоидам и позволит доказать теорем теорему об эволютах к гипоциклоидам.

Теорема 19. Пусть точки А и D движутся по окружности радиуса r₀ с постоянными угловыми скоростями в разные стороны, причём модуль скорости точки D в q (q - положительно) раз больше скорости точки А. Точка М, определяемая условием АМ = 1/(1+q)*AD, описывает гипоциклоиду. Точка В является пересечением линии центров подвижной и неподвижной окружностей с окружностью радиуса r₀-2r₁. Прямая ВМ является касательной к гипоциклоиде и по мере перемещения точки В (с той же угловой скоростью, что и А) вращается с угловой скоростью (1-q)/2.

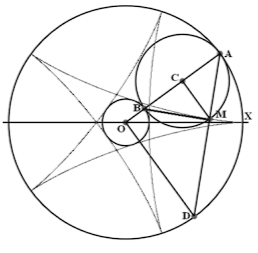
Доказательство. Исходно нам заданы два параметра: радиус неподвижной окружности r0 и отношение q скорости точки D к скорости точки A. Как и выше q = 1-1/k₁, то есть k₁ = 1/(1+q). Кроме того, r₁ = k₁*r₀. 

Таким образом, процесс качения двух окружностей полностью определён, и уже доказано, что точка М описывает гипоциклоиду. Отрезок ВМ является диаметром подвижной окружности. Угол АМВ, опирающийся на этот диаметр является прямым, следовательно прямая ВМ перпендикулярна к нормали AD. Тем самым она является касательной к гипоциклоиде. Предыдущие рассуждения показали, что перпендикулярные друг к другу прямые AD и ВМ вращаются с одинаковой угловой скоростью (1-q)/2. Теорема доказана.

Понятно, что аналогичная теорема может быть сформулирована и для эпициклоид, тем более, что она нами уже доказана.

Теорема 20. Пусть точки В и D движутся по окружности радиуса r₀ - 2*г₁ с постоянными угловыми скоростями в одну сторону, причём модуль скорости точки D в q раз больше скорости точки В. Точка М, определяемая условием ВМ = 1/(1+q)BD, описывает эпициклоиду. Прямая ВМ является касательной к эпициклоиде и по мере перемещения точки В вращается с угловой скоростью (1+q)/2.

Тот факт, что величины r₀ и q могут иметь произвольные значения позволяет переформулировать две последние теоремы в новом виде.

Теорема 21. Пусть по окружности с постоянной угловой скоростью (для определённости равной единице) движется точка, через которую проходит прямая, вращающаяся также с постоянной угловой скоростью ω. Тогда огибающей следов, оставляемых этой прямой, является либо эпициклоида (ω > 0,5), вписанная в эту окружность, либо гипоциклоида (ω < 0,5), описанная вокруг окружности.

Доказательство. Поскольку в теореме одновременно рассматриваются и эпициклоиды, и гипоциклоиды, есть необходимость введения некоторых обобщающих терминов, которые позволят сделать рассуждения более компактными и ясными. Нечто подобное мы уже делали при изучении улиток Паскаля.

В результате качения подвижного круга по ободу неподвижного он заметает кольцо, одной из границ которого является обод неподвижного круга. Вторую границу назовём свободной окружностью (этот термин не является общепринятым). Как эпициклоиды, так и гипоциклоиды находятся внутри этого кольца, которое мы назовём несущим. Отличие случая эпициклоид от случая гипоциклоид состоит в том, что для первых свободная окружность является внешней границей несущего кольца, а для вторых - внутренней. Мгновенный же центр вращения касательной и в том, и в другом случае скользит по свободной окружности.

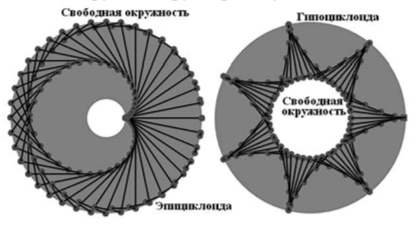
Что касается доказательства теоремы, то оно состоит в том, что по угловой скорости ω восстанавливается параметр q. Действительно, полагая, что q имеет знак, который определяет характер кривой: при q > 0 - эпициклоида, при q < 0 - гипоциклоида, мы можем приравнять угловую скорость ω и величину (1+q)/2, чтобы определить знак параметра q. Поскольку q = 2ω - 1, если ω > 0,5, то q > 0, если же ω < 0,5, то q < 0.

Если q > 0, то q = 1 + 1/k₁ и радиус свободной окружности равен r₀ + 2r₁. Если же q < 0, то -q = 1 - 1/k₁ и радиус свободной окружности равен r₀ - 2r₁. И в том и в другом случае все важные параметры (k₁, r₀, и r₁) восстанавливаются и позволяют воспроизвести процесс построения кривой с помощью качения подвижного круга по неподвижному кругу. При этом семейство касательных к кривой ведёт себя как указано в доказываемой теореме: мгновенный центр вращения касательных движется по окружности с единичной скоростью, а сами касательные вращаются со скоростью ω. Теорема доказана.

Приведём текст программы, производящей построение следов прямой, движущейся так, как указано в теореме 21.

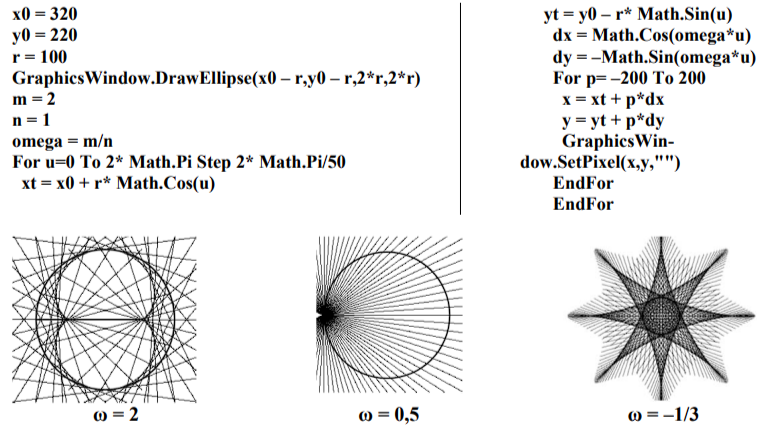
Отметим случай, когда ω = 0,5. Все прямые, полученные при таком вращении проходят через одну точку. Этот факт желательно объяснить на уровне физического воспроизведения процесса построения кривой с помощью качения. И тут выявляется пробел в наших предыдущих рассуждениях. Попытаемся более пристально рассмотреть процесс возникновения циклоидальных кривых. При этом отметим, что теорема 21 помогла нам написать программу построения огибающих, а программа в свою очередь помогла выявить пробел в доказательстве.

Прежде всего, при рассмотрении эпициклоид мы использовали положительные значения параметра k₁, а, значит, q = 1+1/k₁ заведомо больше единицы. Следовательно, пробел в нашем рассуждении приходится на интервал значений q от нуля до единицы. Займёмся его изучением. Поскольку k₁ = 1/(q-1), значения величины k₁ отрицательны (при q = 1 можно условно считать, что k₁ равно минус бесконечности). На отрезке [0; 1] функция k₁ = 1/(q-1) монотонно убывает, и, значит, k₁∈[-∞;-1]. Снова отрицательные величины самовольно врываются в описание физического процесса качения. Необходимо дать правильную интерпретацию их появлению.

Мы достаточно хорошо представляем себе, как происходит построение циклоидальных кривых, когда q∈[1;+∞] и когда q∈[-∞;0]. Если q∈[1;+∞], вычисления показывают, что k1 > 0, и соприкосновение окружностей при качении внешнее. Если q∈[-∞;0], вычисления показывают, что -1 < k₁ < 0, и соприкосновение окружностей при качении внутреннее. Поскольку переход из одной ситуации в другую происходит при k₁ = 0, можно дать следующую геометрическую интерпретацию.

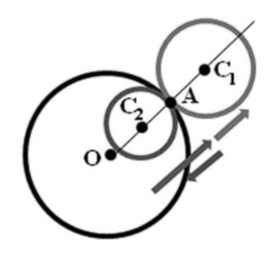
Будем считать, что параметр k₁ принимает любые действительные значения. В этом случае следует признать, что и радиус подвижной окружности может принимать отрицательные значения. Дадим этой возможности следующее геометрическое истолкование. Пусть на плоскости расположены две соприкасающиеся окружности. Одна из них называется неподвижной, а другая - подвижной. Подвижная окружность может либо целиком лежать вне неподвижной, либо целиком лежать внутри этой окружности.

Пусть О - центр неподвижной окружности, С - центр подвижной окружности и А - точка касания этих окружностей. Рассмотрим два вектора ОА и АС и положим, что величина k₁ определяется условием АС = k₁ОА. Такое определение этой величины позволяет ей на законных основаниях принимать отрицательные значения.

Если теперь менять k₁ от некоторого положительного значения к отрицательному, то вектор АС₁ сначала станет нулевым, а потом поменяет направление, а, следовательно, и знак. При этом внешнее касание перейдёт во внутреннее.

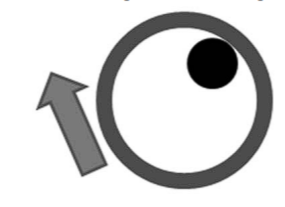
Однако процесс изменения величины k₁ на этом останавливать не обязательно. Когда k1 примет значение -1, неподвижная и подвижная окружности совпадут и качение будет невозможно. Перо останется неподвижным. Это как раз тот самый случай (ω = 0,5), который заставил нас проводить наши рассуждения.

Далее неподвижная окружность станет больше неподвижной и целиком охватит её. Физически эта ситуация вполне допустима. Частично (поскольку полноценного вращения нет) она реализуется, когда на вбитом в стену гвозде раскачивается баранка.

Именно этот случай качения соответствует значениям величины q от нуля до единицы, и, что то же самое, значениям величины k₁ меньше -1.

Итак, наиболее удобным способом единого описания всех трёх ситуаций качения подвижной окружности по неподвижной является использование любых действительных значений для величины k₁.

Поскольку последний случай, при физическом воспроизведении отличающийся от первых двух, то хотя он и выявлен нами, но не рассмотрен в деталях, необходимо и для него получить аналог теорем 12 и 17. При этом первым становится предположение о том, что в случае «баранки» будет вычерчиваться гипоциклоида, ведь значения величины k₁ отрицательны.

Однако достаточно простое рассуждение разрушает эту иллюзию. Пусть q∈[0;1], тогда по свободной окружности в контексте теоремы 13 в одном направлении движутся две точки со скоростями 1 и q. Сторонний наблюдатель не знает, что для нас более быстрая точка имеет скорость 1. Он предположит, что единичную скорость имеет как раз более медленная точка. Это заставит его сделать вывод, что вычерчивается эпициклоида. Это рассуждение можно положить в основу доказательства соответствующей теоремы, но мы пойдём путём подробного рассмотрения кинематики движущейся баранки.

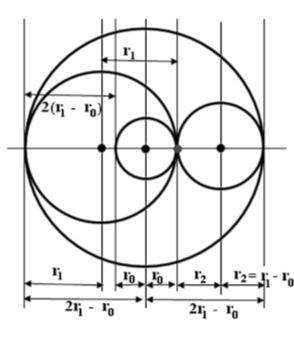
Пусть вокруг неподвижной окружности радиуса r0 катится, охватывая её окружность большего радиуса r₁ (будем считать, что оба радиуса положительны). Процесс качения однозначно определяет свободную окружность радиуса r = 2r₁ - r₀.

Неподвижная окружность радиуса r₀ и свободная окружность являются границами кольца, внутри которого находится вычерчиваемая кривая. Если предположить, что эта линия является эпициклоидой, то из наших предыдущих теорем следует, что такую же эпициклоиду вычертит и перо, связанное с ещё одной окружностью. Эта окружность катится по внешней стороне неподвижной окружности и заметает то же самое кольцо. Радиус этой окружности, как видно из чертежа, равен r₂ = r₁ - r₀. На том же чертеже показано исходное положение пера на двух окружностях.

Итак, наша задача состоит в том, чтобы доказать, что качение «обхватывающей баранки» радиуса r₁ и внешнее качение окружности радиуса r₂ (назовём её внешней) приводит к построению одной и той же эпициклоиды. При этом как всегда будем считать, что r₁ = k₁*r₀, и, значит, r₂ = r₀*(k₁ - 1). По нашему исходному предположению k₁ > 1.

Пусть из исходного положения баранка перекатилась по дуге неподвижной окружности, имеющей угловую меру u. Тогда перо относительно линии центров баранки и неподвижной окружности повернётся на угол u₁ = u*r₀/r₁ = u/k₁. Для внешней окружности выберем такую скорость качения, при которой перо повернётся на такой же угол u₁. Это означает, что внешняя окружность прокатится по дуге длины u₁*r₂ = u/k₁*r₀*(k₁-1). Таким образом, угловая мера соответствующей дуги на неподвижной окружности равна u₂ = u₁*r₁/r0 = u*(1-1/k₁) = u-u₁. Но из этого следует, что радиус внешней окружности С_внешнМ, на котором расположено перо, параллелен линии центров неподвижной окружности и баранки ОС_{баранки}.

Точно так же угол наклона радиуса баранки С_{баранки}М, на котором расположено перо, равен u-u₁. Следовательно, этот радиус параллелен линии центров неподвижной и внешней окружностей ОС_внешн.

Мы некорректно использовали одну и ту же букву M для обозначения перьев на баранке и внешней окружности, поскольку на самом деле эти перья совпадают. Действительно, через точку Свнешн проведём прямую параллельную ОС_{баранки}, а через точку С_{баранки} - прямую параллельную ОС_внешн. Точка их пересечения М очевидно совпадает и с одним, и с другим пером. Более того, поскольку ОС_внешнМС_{баранки} параллелограмм, точка М является точкой пересечения баранки и внешней окружности.

Отметим, что в исходном положении центры баранки и внешней окружности максимально удалены друг от друга, тем не менее, они касаются друг друга внешним образом. При их свободном перемещении внутри кольца возможно и внутреннее касание. Во всех прочих положениях баранка и внешняя окружность имеют две точки пересечения. Сразу возникает вопрос, по какой траектории движется вторая точка пересечения. Но об этом поговорим позже.

Таким образом, мы доказали, что и с помощью баранки, и с помощью внешней окружности вычерчивается одна и та же кривая. Но, поскольку внешняя окружность, как нам известно, связана с эпициклоидой, то установлен и тип этой кривой. Полученные нами результаты позволяют написать программу, воспроизводящую данный процесс. А программа даст нам возможность рассмотреть процесс качения сразу двух окружностей более пристально.

Кроме построения эпициклоиды программа должна воспроизвести хотя бы один кадр качения баранки и внешней окружности. Она также должна выделить точки их соприкосновения с неподвижной и свободной окружностями и начертить важные прямые, соединяющие выделенные точки.

Теорема 22. Пусть по неподвижной окружности радиуса r₀ без проскальзывания катятся баранка радиуса r₁ (r₁ = k₁r₀; r₁ > r₀) и внешняя окружность радиуса r₂ = r₁ - r₀. При этом качение происходит так, что центр баранки движется с единичной угловой скоростью, а центр внешней окружности - с угловой скоростью 1 - 1/k₁. Тогда одна из точек пересечения баранки и внешней окружности вычерчивает эпициклоиду, касательная к которой проходит через точки касания баранки и внешней окружности со свободной окружностью, а нормаль - через точки их касания с неподвижной окружностью.

Доказательство. Факт вычерчивания эпициклоиды нами уже установлен ранее. Остаётся доказать утверждения о касательной и нормали. Это легко сделать, исползуя чертёж, построенный нашей последней программой.

Как доказано выше, ОС_внешнМС_{баранки} является параллелограммом. Из этого следует, что углы при вершинах равнобедренных треугольников В_внешнС_внешнМ и В_внешнОВ_{баранки} равны. Значит, равны и углы при основаниях, то есть отрезки В_внешнМ и В_внешнВ_{баранки} лежат на одной прямой.

Угол А_{баранки}МВ_{баранки} опирается на диаметр баранки, следовательно, является прямым. Угол А_внешнМВ_внешн опирается на диаметр внешней окружности, следовательно, также является прямым. Значит, точки А_{баранки}, А_внешн и М лежат на одной прямой. Кроме того, как мы знаем, через мгновенные центры вращения катящихся окружностей А_{баранки} и А_внешн проходят нормали к эпициклоиде. Наконец, эти нормали (вернее одна нормаль, поскольку они сливаются воедино) перпендикулярны прямой В_{баранки}В_внешн. Таким образом, она является касательной к эпициклоиде. Теорема доказана.

Отметим, что мы легко могли бы получить отношения, в которых точка М делит как отрезок В_{баранки}В_внешн, так и отрезок А_{баранки}А_внешн. Однако мы предоставляем сделать это читателю.

К данному моменту мы установили, что переход к баранкам (k₁ < -1) не привёл к появлению новых кривых. Тем не менее, он позволил установить новые факты об уже известных нам циклоидальных кривых.

Вкратце коснёмся вопроса о второй точке пересечения баранки и внешней окружности. Осуществляя их качение по условию, указанному в теореме 22, будем вычислять координаты точек пересечения двух соответствующих окружностей. Для этого решается система двух уравнений второго порядка, а именно система, состоящая из уравнений этих окружностей. Для её решения из одного уравнения вычитается другое, что приводит к линейному уравнению. Это уравнение описывает прямую, проходящую через точки пересечения окружностей, и позволяет получить квадратное уравнение относительно переменной х после исключения переменной у. Именно таков смысл вычислений, производимый в предлагаемой ниже программе, которая строит траектории обеих точек пересечения баранки и внешней окружности.

Конкретный вариант, использованный в программе, позволяет убедиться, что вторая точка пересечения баранки и внешней окружности описывает траекторию с циклоидальными кривыми никак не связанную, хотя первая точка вычерчивает хорошо нам знакомую кардиоиду. Соответствующую кривую можно назвать сопряжённой к эпициклоиде. В случае кардиоиды мы видим, что сопряжённая линия имеет каплеобразную форму. Возможно, что перед нами некий новый вид кривых. По крайней мере, их желательно исследовать, что мы и предоставляем читателю, поскольку подобное исследование очень далеко увело бы нас от целей данной статьи.

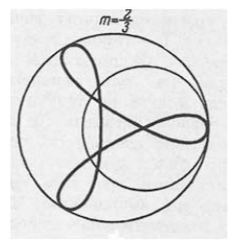
Вернёмся к гипоциклоидам и сделаем одно вполне естественное наблюдение. Оно состоит в следующем. При значениях параметра k₁, в интервале от нуля до -1/2, мы имеем ясную картину построения гипоциклоиды. В то же время при значениях параметра k₁, в интервале от -1/2 до -1, такой чёткой картины нет. К тому же подвижная окружность получает некоторые свойства баранки, только охватывает она не неподвижную окружность, а круг, ограниченный свободной окружностью. В книге [3] на странице 112 сообщается, что при m > 1/2 (m играет роль k₁ без знака) вместо точек возврата у гипоциклоиды возникают узловые точки. Это утверждение иллюстрируется рисунком.

На самом деле это утверждение ошибочно. Оказывается, что здесь действительно возникает своеобразный эффект баранки, которая нового не создаёт, а только повторяет нечто известное. При этом имеет место полная аналогия с теоремой 22.

Теорема 23. Пусть по внутреннему ободу неподвижной окружности радиуса r₀ без проскальзывания катятся две окружности радиуса r₁ (r₁ = k₁r₀; 1 > k₁ > 0,5) и окружность радиуса r₂ = r₀ - r₁. При этом качение происходит так, что центр первой окружности движется с единичной угловой скоростью, а центр второй окружности - с угловой скоростью 1 - 1/ k₁ (эта скорость отрицательна). Тогда одна из точек пересечения двух катящихся окружностей вычерчивает гипоциклоиду. Касательная к ней проходит через точки соприкосновения двух движущихся окружностей со свободной окружностью, а нормаль - через точки их соприкосновения с неподвижной окружностью.

Доказательство. Факт вычерчивания гипоциклоиды пером второй окружности нами уже установлен ранее. Нужно доказать, что и перо первой окружности вычерчивает ту же кривую, а также утверждения о касательной и нормали. Поскольку формулировка теорем 22 и 23 практически одинакова, их доказательства также мало отличаются друг от друга. По этой причине мы приводим соответствующий чертёж и отмечаем, что выбор угловых скоростей, сделанный нами обеспечивает параллельность прямых ОС₁ и С₂М, а также прямых ОС₂ и С₁М. Это и обстоятельство является основой доказательства теоремы.

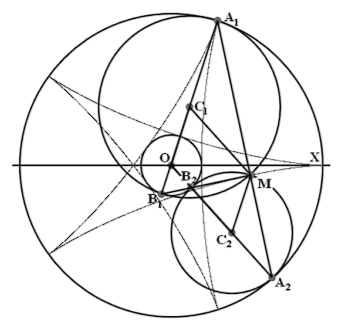
Теоремы 22 и 23 можно было бы объединить в одну, но вместо этого мы сформулируем общее для эпициклоид и гипоциклоид обобщение теоремы 14.

Теорема 24. Эволютой как эпициклоиды, так и гипоциклоиды является точно такая же кривая, для эпициклоид вписанная в неподвижную окружность, а для гипоциклоид описанная вокруг неподвижной окружности.

Доказательство. В теоремах 22 и 23 фактически доказано, что нормаль эпициклоид и гипоциклоид вращается вокруг точки, движущейся с единичной скоростью по неподвижной окружности с тою же угловой скоростью, что и касательная. Из теоремы 21 следует нужное нам утверждение. Теорема доказана.

Приведём в качестве иллюстрации небольшую программу.

Вернёмся к вопросу о том, что циклоидальные кривые можно рассматривать как образное представление действительных чисел. Здесь мы встретились с неожиданным ограничением. «Баранки» не вносят ничего нового в класс этих кривых. По этой причине термин «перициклоиды» [3, стр. 111] либо является излишним, либо может характеризовать только конкретный способ построения кривой. Об этом обстоятельстве без обоснования говорится в [4].

Итак, при образном представлении действительных чисел речь может идти только о числах в пределах от -2 до +∞ . Начнём с рассмотрения этих крайних случаев.

Если k₁ = -0,5, то q = -1. Это означает, что точки В и D движутся из исходного положения с равными скоростями в противоположных направлениях, то есть хорда Bd всегда остаётся вертикальной. Кроме того, точка М является серединой этой хорды, а, значит, скользит по горизонтальному диаметру. Таким образом, соответствующая гипоциклоида является отрезком. Впрочем, это утверждение не совсем точно. Правильнее было бы назвать её окружностью, сплющенной в отрезок, поскольку точка М пробегает по горизонтальному диаметру два раза. Подробнее мы вернёмся к этому вопросу при изучении трохоид.

Теперь поговорим о случае k₁ = +х. Зафиксируем неподвижную окружность, а радиус подвижной будем неограниченно увеличивать, увеличивая k₁. В итоге подвижная окружность превратится в прямую, которую мы и будем воспринимать, как окружность бесконечного радиуса.

Наших рассуждений, основанных на не слишком строгих, интуитивных основаниях, тем не менее, достаточно для построения хотя бы небольшого фрагмента соответствующей кривой. Как целое, она, по понятным причинам должна походить на спираль Архимеда и удаляться от центра неподвижной окружности сколь угодно далеко во всех направлениях.

Приведём соответствующую программу, которая построит нашу кривую. Однако ещё до построения мы можем отметить одно важное обстоятельство. Дело в том, что мы можем понять, что за кривую мы строим. Более того, мы уже встречались с ней в первой части статьи. Дело в том, что качение прямой по неподвижной окружности без проскальзывания эквивалентно сматыванию натянутой нити с окружности. Как мы знаем, эта процедура приводит к построению эвольвенты окружности. Добавим ещё, что после разрезания нити, намотанной на окружность, её можно сматывать в разные стороны.

Теперь обсудим внешний вид гипоциклоид. При этом вспомним, что эпициклоиды, соответствующие параметру k₁ = m/n состоят из n арок, огибающих неподвижную окружность m раз. Особенно наглядно это проявляется в случае, когда m < n. Арки не имеют непомерной длины, то есть не обкручиваются вокруг неподвижной окружности по нескольку раз.

Для гипоциклоид имеет место то же самое строение. Только арки находятся внутри неподвижной окружности. Более того, можно провести аналогию между гипоциклоидами и правильными звёздчатыми многоугольниками, вписанными в окружность. Каждая такая звезда определяется числом лучей (для гипоциклоиды - арок) и количеством обходов вокруг центра неподвижной окружности. Других гипоциклоид не существует.

Итак, на настоящий момент мы достаточно хорошо представляем себе, как выглядят эпициклоиды и гипоциклоиды. Кроме того, мы знаем, что ряд свойств этих кривых, изучаемых в рамках дифференциальной геометрии, может быть получен с помощью методов элементарной геометрии и достаточно простых соображений, связанных с кинематикой. Речь идёт о построении касательных, нормалей и эволют. Именно по этой причине мы и считаем, что изучение подобных кривых является прекрасным введением в более сложную геометрическую проблематику.

Вспомним также о том, что каждая из эпи- и гипоциклоид связана с числом k₁ из интервала [- 2; ∞] и по этой причине может рассматриваться как зримый образ соответствующего действительного числа. При этом кривые, соответствующие иррациональным числам, имеют достаточно простую структуру - арки, обвивающие неподвижную окружность (для эпициклоид). В то же время, поскольку процесс построения «иррациональных» эпициклоид никогда не может завершиться, мы имеем дело с достаточно необычными объектами. Но рассмотрение таких объектов на ранних стадиях изучения высшей математики весьма полезно по ряду причин. Укажем только на их связь с фундаментальными фактами классической механики, например с теоремой Пуанкаре о возвращении: «почти всякая движущаяся точка
 многократно возвращается к своему исходному положению. Это - один из немногих общих выводов о характере движения» [5].

Теперь, оставляя тему представления вещественных чисел эпи- и гипоциклоидами, попытаемся соединить воедино некую совокупность этих кривых. Сразу оговоримся, что можно было бы создать соответствующую конструкцию, включающую все кривые, но мы ограничимся эпициклоидами, соответствующими отрезку k₁∈[1;2].

Рассмотрим прямой круговой цилиндр, во все горизонтальные сечения которого следующим образом впишем эпициклоиды. Выберем одну из вертикальных образующих цилиндра и отобразим на неё отрезок [1; 2]. Теперь любому горизонтальному сечению соответствует параметр k₁∈[1;2]. Каждая точка выбранной образующей станет исходной точкой для построения эпициклоиды по способу, описанному в теореме 13 с параметром k₁, соответствующим данному сечению. Например, в нижнее основание цилиндра будет вписана кардиоида. В результате из совокупности всех эпициклоид мы получим нечто среднее между поверхностью и телом.

Все сечения порождены сходным механическим процессом, скорости в котором непрерывно меняются при переходе от сечения к сечению, то есть в вертикальном направлении между кривыми существуют непрерывные маршруты, одним из которых является выбранная нами образующая. С другой стороны «рациональным» эпициклоидам соответствуют замкнутые кривые конечной длины, а «иррациональным» - плотно заполняющие кольцевые области.

Все два вида этих сечений основательно перемешаны, так же как перемешаны на числовой прямой рациональные и иррациональные числа. Предоставляем читателю возможность более подробно изучить соответствующий объект.

Мы же возвращаемся к классическим результатам теории циклоидальных кривых и займёмся уравнениями эпициклоид и гипоциклоид. Нашей непосредственной целью является вывод уравнения, одновременно описывающего оба вида кривых. При этом мы попытаемся показать, что работа с уравнениями не обязательно сводится к цепочке формальных преобразований. Она может быть вполне осмысленной, если исследователь ясно понимает геометрический (или кинематический) смысл уравнения или отдельных его членов. Демонстрация этого обстоятельства может иметь значительный педагогический эффект.

Прежде всего, сопоставим полученные на данный момент уравнения эпициклоид и гипоциклоид.

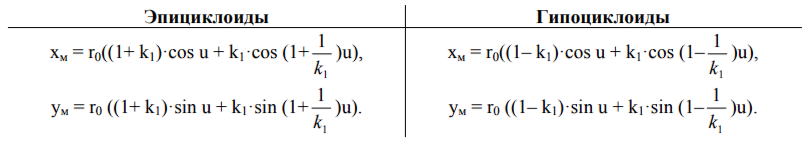
Сходство не может не бросаться в глаза. Однако замена параметра k₁ в уравнениях эпициклоид на -k₁ приводит к уравнениям, в которых в правой части стоят не суммы, а разности. Вроде бы, мелочь, но она всё портит. Придётся с ней разбираться. В этом нам поможет теорема, установленная Франсуа [3, стр 116]. Сразу отметим, что приведённая в книге А. А. Савёлова формулировка не верна. Как мы увидим позднее, при произвольном выборе длин сторон шарнирного параллелограмма и при произвольном выборе угловых скоростей, четвёртая вершина вычерчивает либо эпитрохоиду, либо гипотрохоиду. Сейчас же мы сформулируем теорему для случая эпициклоид и гипоциклоид. 

Теорема 25. Можно подобрать угловую скорость q, чтобы две стороны ON и OK шарнирного параллелограмма вращались равномерно с угловыми скоростями 1 и q, а четвёртая вершина М описывала либо эпициклоиду (q > 0), либо гипоциклоиду (q < 0).

Доказательство. Для доказательства используем наши уравнения. При этом будем иметь в виду, что уравнения вида x = r*cosω*u и y = r*sinω*u описывают движение точки по окружности радиуса r с постоянной угловой скоростью ω. Таким образом, каждую пару уравнений можно рассматривать как уравнение эпициклоиды или гипоциклоиды, либо как описание координат вершины М шарнирного параллелограмма.

При этом точка N движется с единичной угловой скоростью по окружности радиуса r_b = (1 ± k₁)-r₀, а точка К - со скорость q по окружности радиуса r_m = k₁r₀. Продемонстрируем это утверждение на соответствующих чертежах, отдельно для эпициклоид и циклоид. При этом за исходные параметры мы будем брать величины k1 и ro. Соответствующие же радиусы r_b и r_m будут вычисляться с помощью величин k₁ и r₀. Кроме того, ясно, что q = 1 ± 1/k₁, в зависимости от направления вращения.

Теперь мы можем опираться на теоремы 13 и 17. Заодно отметим, что в теоремах 22 и 23 речь фактически уже шла о соответствующих параллелограммах, но там они появлялись в связи с качением окружностей и в довольно сложном контексте. В теореме же Франсуа всё предельно просто. Как мы знаем, отрезок ОВ и лежащий на нём отрезок ON вращаются с единичной угловой скоростью. Отрезок OD и лежащий на нём отрезок OK вращаются с угловой скоростью q.

Хорда BD проходит через точку М циклоидальной кривой, причём BM/BD = 1/(1±q). Ниже мы рассмотрим только случай эпициклоиды, поскольку в случае гипоциклоиды доказательство проводится аналогичным образом. Итак, поскольку

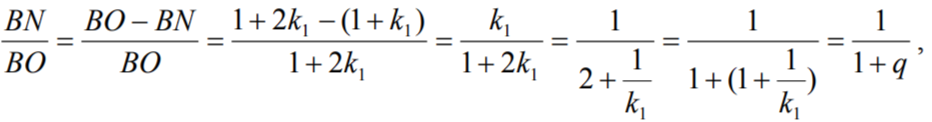
треугольники BMN и BDO подобны, а, следовательно, отрезок MN параллелен отрезку ОК. Точно также отрезок МК параллелен отрезку ON. В результате мы установили, что четырёхугольник ONMK является параллелограммом.

Теперь предположим, что нам исходно заданы два параметра rb и rm, а именно длины сторон параллелограмма. Тогда из уравнений rb = (1 ± k1)-r0, и rm = krr0 находим r0 и k1, а, значит, и q. После этого мы убеждаемся, что наш шарнирный параллелограмм позволяет построить нужную кривую. Теорема доказана.

Используя уравнения циклоидальных кривых, мы пришли к теореме Франсуа. Теперь мы с помощью этой теоремы сделаем некоторые выводы об этих уравнениях.

В теореме говорится только о длине сторон шарнирного параллелограмма и их угловых скоростях. Начальное положение этих сторон может быть выбрано любым. Вне зависимости от этого будет построена вполне определённая циклоидальная кривая. Исходные же углы наклона сторон влияют только на поворот кривой вокруг центра неподвижной окружности. Действительно, поскольку стороны параллелограмма вращаются с различными скоростями, рано или поздно они догонят друг друга, вопреки злопыхательским утверждениям Зенона Элейского. Этот момент определит тот или иной угол поворота кривой.

Таким образом, уравнения

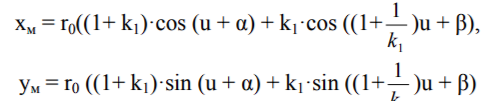
являются уравнениями эпициклоиды, повёрнутой на некоторый угол. Пусть, например, а = 0, а ß = п, тогда уравнения принимают вид

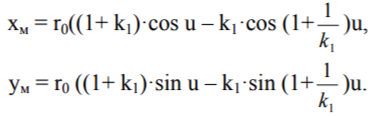
Теперь замена параметра k1 на -k1 переводит уравнения эпициклоиды в уравнения гипоциклоиды.

Метод Франсуа позволяет перейти к описанию эпициклоид и гипоциклоид с помощью комплексных чисел [3, стр. 116]. Действительно, вращение стержня длины s с угловой скоростью ю на комплексной плоскости описывается уравнением z = s • e^ωti. Из этого следует, что в соответствии с теоремой Франсуа уравнение z = s1е^ti + s2^qti при соответствующем выборе параметра q описывает эпи- или гипоциклоиду. Это обстоятельство позволяет конформно отображать внутренность окружности на внутреннюю область, ограниченную эпициклоидами, соответствующими целым числам, и внешнюю область, ограниченную гипоциклоидами, соответствующими аликвотным дробям (то есть вида 1/n).

Отметим также, что подобная форма описания циклоидальных кривых позволяет получить обобщение, предложенное Беллерманом [3, стр. 116], которое приводит к так называемым циклоидам высших порядков. При этом рассматривается сумма нескольких вращающихся с постоянными, но различными угловыми скоростями векторов-стержней. Общее уравнение имеет вид . Циклоиды высших порядков также связаны с конформными отображениями.

Возможно и обобщение, приводящее к пространственным кривым. В многомерном пространстве выбираем несколько двумерных плоскостей, проходящих через начало координат, и начинаем вращать в каждой из них радиус-вектора. Суммарный вектор вычерчивает пространственную кривую.

9. ГИПОТРОХОИДЫ

Перейдём к изучению удлинённых и укороченных гипотрохоид. Так же, как и в разделе, посвящённом гипоциклоидам, мы будем возвращаться и к эпитрохоидам. Особое наше внимание привлечёт различие в форме удлинённых и укороченных трохоид, поскольку именно оно играет важную роль при построении упомянутых выше конформных отображений.

Теорема 26. Пусть точки В и D движутся по окружности радиуса r0 - r1 +r2 с постоянными скоростями в разные стороны (r1 = к1-г0; k1 < 0,5; г2 = к2-г1). Если скорость точки Вравна единице, а скорость точки D равна q = 1 - 1/k1 (эта скорость отрицательна), то точка М, такая, что ВМ = r2/(r0-r1+r2)BD вычерчивает гипотрохоиду.

Доказательство. Точно так же, как гипоциклоида в теореме 17, гипотрохоида строится с помощью неподвижной окружности радиуса г0 с центром О и подвижной окружности радиуса г1 с центром С (г1 = к1r0) пером, удалённым от центра подвижной окружности на расстояние г2. При этом качение осуществляется по внутренней стороне обода.

Пусть линия центров ОС, на которой лежат точки А и В, движется против часовой стрелки и имеет угол наклона u. Длина дуги неподвижной окружности, по которой прокатилась подвижная окружность, равна г0*и. Такова же и длина дуги подвижной окружности, пришедшей в соприкосновение с неподвижной. Центральный угол, опирающийся на эту дугу, равен u1 = u*r0/r1 = u/k1.

Выберем точку D так, чтобы ∠ BoD = u - u1. Пусть из исходного положения на горизонтали перо переместится в точку М. Как показано в теореме 17, ∠ ВСМ = u - u1. Треугольники OBD и СВМ являются равнобедренными и имеют углы при вершинах равные u1. Значит, у них равны и углы при основании, то есть ∠ СВМ = ∠ OBD = (П-u1)/2 . Из этого следует, что точка М лежит на хорде BD. Из подобия названных треугольников следует, что ВМ = r2/(r0-r1+r2). Теорема доказана.

Теперь, используя теоремы 15 и 26 выведем уравнения эпи- и гипотрохоид. Вывод делается аналогично тому, как это уже было проведено для эпи- и гипоциклоид.

Параметрические уравнения эпитрохоиды с параметрами г1 = к1r0, г2 = к2r1, q=1+1/k1, r2 г = г0 + г1 + г2 и t = r2/(r0+r1+r2) имеют вид:

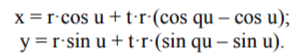
Раскрыв скобки и вводя новые обозначения для коэффициентов при cos u и cos qu (с1 = r-t*г; c2 = t*r), получим уравнения в виде:

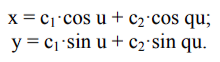
Параметрические уравнения гипотрохоиды с параметрами r1 = k1*r0, r2 = k2*r1, q = 1-1/k1, r = r0-r1+r2 и t = r2/(r0-r1+r2) имеют вид точно такой же вид и приводятся к тем же окончательным уравнениям. Итак, мы установили, что эпи- и гипотрохоиды описываются уравнениями вида:

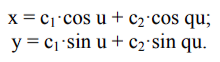
Таким образом, общая теорема Франсуа может быть сформулирована следующим образом.

Теорема 28. Если стороны On (длина стороны с1) и OK (длина стороны с2) шарнирного параллелограмма вращались равномерно с угловыми скоростями 1 и q, то четвёртая вершина М описывает либо эпитрохоиду (q > 0), либо гипотрохоиду (q < 0).

Сразу отметим, что поскольку с1 = r - t-r и c2 = t-r, то с1 + с2 = г, то есть кривая вписана в окружность радиуса с1 + с2. Очевидно, характер кривой зависит не от самих значений с1 и с2, а от их отношения. Действительно, если пропорционально изменить длину сторон параллелограмма, то будет вычерчена гомотетичная кривая. Таким образом, коэффициенты с1 и с2 в уравнениях можно пропорционально изменять. В частности можно привести уравнения к виду:

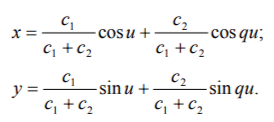
Теперь нам нужно разобраться в том, какие кривые получаются при различных значениях с1 и с2. В последних уравнениях r = 1, а, значит, t = c2/(c1+c2).

Далее, как мы знаем, значение параметра t, позволяющее построить эпи- или гипоциклоиду равно либо 1/(1+q) для положительных q (случай эпициклоиды), либо 1/(1-q) для отрицательных q (случай гипоциклоиды).

В принципе данный результат аналитическим путём мы могли получить уже давно. Для этого достаточно было использовать параметрические уравнения трохоид и теоремы 13 и 18. Однако мы стараемся обрисовать ситуацию более детально. И хотим показать, где возможно, геометрические и кинематические механизмы, связанные с возникновением циклоидальных кривых.

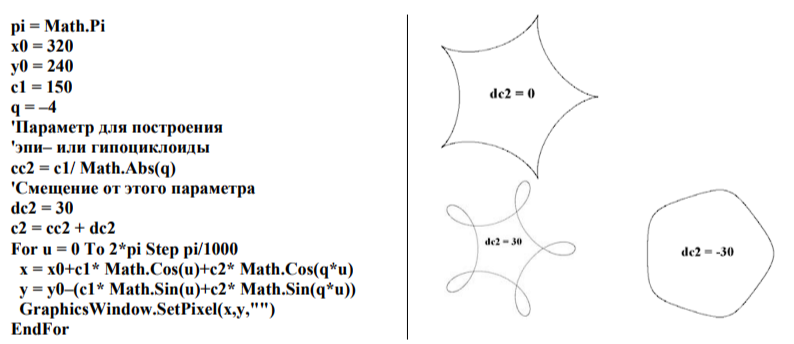
Продемонстрируем наши выводы с помощью очередной программы. В ней мы вычислим значение параметра с2, дающего эпи- или гипоциклоиду, и сохраним это значение в переменной сс2. Параметр dc2 (добавка к с2) служит для получения отклонения коэффициента с2 от этого важного значения. При dc2 > 0 величина с2 растёт, строится удлинённая эпитрохоида. При dc2 < 0 с2 убывает, и строится укороченная эпитрохоида. Для гипотрохоид все вычисления и результаты построений аналогичны.

 

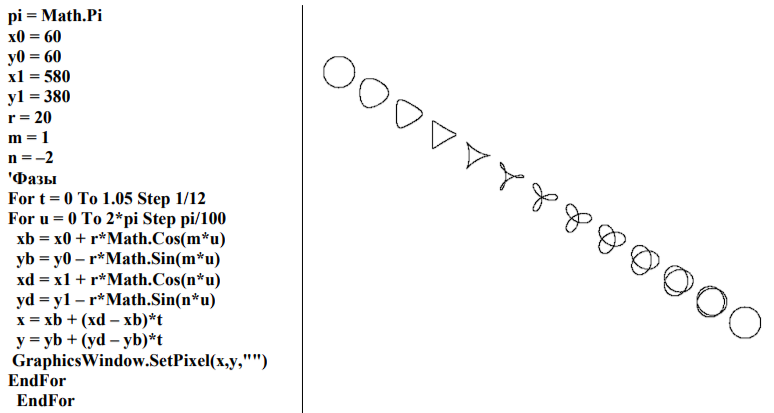
Определённый интерес представляет вопрос об образовании различных семейств циклоидальных кривых. Мы уже рассматривали в связи с теоремой 16 семейство эпитрохоид, являющихся следами гомотопического перетекания одинарной петли-окружности в n- разовую петлю-окружность. Аналогичное семейство можно построить и для гипотрохоид. В этом случае, однако, у исходной и конечной петель направления обхода будут иметь противоположные направления. Простая программа демонстрирует переход m-разовой петли-окружности в n-разовую при условии, что m положительно, а n отрицательно.

Мы видим, как укороченные эпициклоиды становятся элементами визуализации сеток соответствующих конформных отображений. Отметим, что они не пересекаются друг с другом.

Если же рассмотреть функцию w = c*q*z+c*z^q при любых значениях переменной z, то она переводит любую окружность вида |z| = const в семейство эпитрохоид. Но, естественно, что удлинённые эпитрохоиды не только обладают точками самопересечений, но и пересекают другие кривые.

Той же самой программой, сделав верхний предел изменения переменной r больше единицы, можно построить подобное расширенное семейство. На чертеже показан случай для q = 2. Таким образом, семейство строится с помощью функции w = 2*z+z² и состоит из улиток Паскаля.

Пусть теперь q является отрицательным целым числом. Функция w = c • |q| • z + c • z^q уже не является аналитической внутри круга |z| < 1. Более того, в случае |q| > 1 в нуле она имеет кратный полюс [8]. Изменим функцию так, чтобы она, как и прежде отображала окружности в гипотрохоиды, но при этом имела бы простой полюс.

Для этого заставим стороны параллелограмма вращаться в противоположных направлениях. Точнее, сторона, которая вращалась с угловой скоростью 1, теперь будет вращаться с угловой скоростью -1, а сторона, которая вращалась с угловой скоростью q, теперь будет вращаться с угловой скоростью -q (напомним, что q < 0). Ясно, что кривая по методу Франсуа будет построена та же самая. Зато теперь мы можем использовать функцию с простым полюсом w = -(c*q)/z+c*z^-q. И в этом случае [7, глава II, теорема 3] функция осуществляет конформное отображение круга |z| ≤ 1 на внешность гипоциклоиды.

Последняя из наших программ при минимальной модификации позволяет строить соответствующие семейства гипотрохоид. Пока эти гипотрохоиды являются укороченными, они не пересекаются и заполняют внешнюю область гипоциклоиды.

 

Теперь перейдём к рассмотрению конкретных видов гипоциклоид и гипотрохоид. Начнём с очень простого, но интересного случая q = -1. Будем пользоваться теми же обозначениями, которые использовались в теореме 26. Поскольку радиусы ОВ и Öd вращаются в противоположных направлениях с одинаковой угловой скоростью, точки В и D всё время симметричны относительно горизонтальной прямой, проходящей через центр вращения. Таким образом, хорда BD всегда перпендикулярна к горизонтали.

Точки, которые делят эту хорду в постоянном отношении, вычерчивают гипоциклоиды. Каждая из них является сжатой окружностью, а сама гипоциклоида представляет собой эллипс, сжатый в горизонтальный диаметр.

Функция, которая осуществляет конформное отображение круга |z| < 1 на внешность гипоциклоиды, то есть на плоскость с удалённым отрезком, задаётся формулой w = z+1/z Нетрудно видеть, что с точностью до множителя 1/2 перед нами функция Жуковского. Разберёмся, для чего введён этот множитель.

Дело в том, что без него функция w = z+1/z переводит точку z = 1 в точку w = 2. То есть гипоциклоида представляет собой отрезок [-2; 2]. Добавление же этого множителя подстраивает гипоциклоиду-отрезок так, чтобы она стала вписанной в окружность единичного радиуса.

Если подобную подгонку сделать и для всех других гипоциклоид, то уравнение w = q/z+z², где q - натуральное число, следует заменить на уравнение w = (q/z+z^q)/(q+1).

Далее мы рассмотрим две наиболее известные гипоциклоиды. Одной из них является астроида (q = -3), а второй - кривая Штейнера (q = -2), которая особенно важна для нас.

Согласно теореме 21 астроида является огибающей некоторого семейства прямых, которое можно описать следующим образом: точка Т движется по окружности постоянной угловой скоростью против часовой стрелки, а прямая, проходящая через точку Т, вращается с такой же угловой скоростью по часовой стрелке.

Теорема 29. Астроида является огибающей отрезков постоянной длины, концы которых скользят по двум взаимно перпендикулярным прямым.

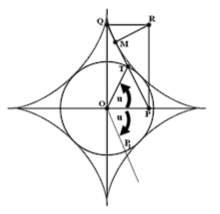
Доказательство. Пусть радиус ОТ, имеющий длину г, вращается против часовой стрелки, а прямая ОР1 вращается по часовой стрелке с такой же угловой скоростью. Тогда прямая ТР, которая параллельна прямой ОР1, является касательной к астроиде. Очевидно, что треугольник ТОР является равнобедренным. Точно также равнобедренным является и треугольник TOQ (отрезок TQ является продолжением отрезка ТР). Значит, ТР = TQ = ОТ = г, а, следовательно, PQ имеет постоянную длину, равную 2r. Теорема доказана.

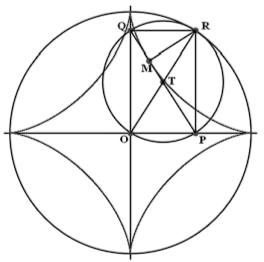
Следуя [3], рассмотрим способ построения астроиды с помощью, так называемых, кардановых кругов. Первый и больший из них имеет радиус 2r. К тому же он разделён на четыре части двумя перпендикулярными диаметрами. Второй круг имеет радиус r и катится по внутреннему ободу первого круга. Пересекаясь с диаметрами, он в каждом своём положении задаёт точки Р и Q из теоремы 29. Как мы знаем, прямая PQ является касательной к астроиде.

Одна из точек малого карданова круга вычерчивает астроиду, двигаясь вдоль касательной ортогонально радиусу, проходящему через неподвижную в данный момент точку R. Таким образом, ею может быть только точка М, которая является основанием перпендикуляра, опущенного из точки R мгновенного соприкосновения кардановых окружностей на касательную PQ.

Поскольку при качении малого карданова круга естественным образом возникает прямоугольник OQRP, то можно сказать, что астроида является геометрическим местом оснований перпендикуляров Rm, опущенных из точки R на диагональ PQ.

10. КРИВАЯ ШТЕЙНЕРА

Кривая Штейнера является нашей главной целью. Именно с её помощью будет построена соответствующая группа преобразований.

Кривая Штейнера возникает при качении подвижной окружности по внутреннему ободу неподвижной окружности. При этом радиус подвижной окружности в три раза меньше радиуса неподвижной окружности. Легко понять, что кривая Штейнера состоит из трёх арок. Она похожа на греческую букву дельта и, по этой причине, её порой называют дельтоидой.

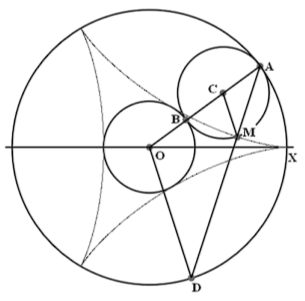
Согласно теореме 19 кривая Штейнера может быть построена следующим образом. Пусть точки А и D движутся по окружности радиуса r0 с постоянными угловыми скоростями в разные стороны, причём модуль скорости точки D в два раза больше скорости точки А. Точка М, определяемая условием АМ = 3 Ad, описывает дельтоиду.

Если угол АОХ равен u, то будем говорить, что точка А определяется углом u. Рассмотрим кроме точки А ещё и точку А1, которая определяется углом u + п. Назовём точки А и А1 связанными, а отрезок АА1 - диаметром кривой Штейнера.

Наконец вспомним, что согласно теореме 21 кривую Штейнера можно построить как огибающую некоторого семейства прямых. Пусть по окружности радиуса 1/3*r0 с постоянной угловой скоростью ω1 движется точка, через которую проходит прямая, вращающаяся также с постоянной угловой скоростью ω2. Тогда в случае, когда ω2/ω1 = -1/2 огибающей следов, оставляемых этой прямой, является кривая Штейнера, описанная вокруг окружности радиуса 1/3*r0 (речь идёт о свободной окружности).

Теперь у нас есть возможность сформулировать интересную теорему о кривой Штейнера.

Теорема 30. Любой из диаметров кривой Штейнера касается этой кривой и имеет постоянную длину, равную удвоенному диаметру катящейся окружности. Касательные, проведённые через концы диаметра, перпендикулярны друг другу, а точка их пересечения лежит на окружности радиуса 1/3*r0.

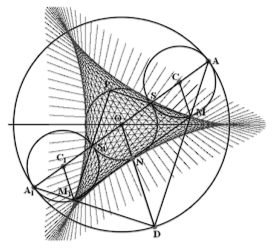
Доказательство. Пусть точка А определяется углом u, а связанная с ней точка А1 - углом u + п. Тогда точки D и D1, по теореме 19 соответствующие точкам А и А1, определяются углами -2u и -2u + 2п, то есть D и D1 совпадают. Поскольку отрезок АА1 является диаметром неподвижной окружности, угол ADA1 - прямой.

Поскольку АМ = 1/3AD, так же как и АМ1 = 1/3A1D1, то подобны пары треугольников OAD и САМ, а так же ОА1D и СА1М1. Из этого следует, что отрезки СМ и С1М1 параллельны и равны. Таким образом, четырёхугольник МСС1М1 является параллелограммом. Значит, диаметр кривой Штейнера ММ1 параллелен отрезку АА1 и равен двум диаметрам катящейся окружности.

Кроме того, диаметр кривой Штейнера ММ1 наклонён к горизонтали под углом u (в силу параллельности отрезку АА1) и проходит через точку N, лежащую на пересечении свободной окружности и отрезка OD, который наклонён к горизонтали под углом -2u. Получается, что любой из диаметров кривой Штейнера лежит на прямой NM, причём точка N движется с угловой скоростью -2, а прямая NM вращается с угловой скоростью 1. По теореме 21 получается, что диаметры кривой Штейнера касаются этой кривой.

Теперь проведём в точках М и М1 касательные к кривой Штейнера. Поскольку AD - нормаль к этой кривой, то отрезок MS, соединяющий точку М на кривой с точкой S пересечения катящейся окружности с отрезком АА1 является касательной. Действительно, угол SMA опирается на диаметр катящейся окружности и является прямым, то есть AD и MS перпендикулярны.

Точно также отрезок MS1, соединяющий точку М1 на кривой Штейнера с точкой S1 пересечения катящейся окружности в новом её положении с отрезком АА1 является касательной.

Поскольку отрезки AD и AD1 перпендикулярны, перпендикулярны друг другу и касательные MS и MS1. А поскольку они исходят из концов диаметра SS1 свободной окружности, то пересекаются в некой точке Р, лежащей на этой же окружности. Теорема доказана.

Видимо, тот факт, что кривая Штейнера является огибающей своих диаметров, привёл к появлению так называемой задачи об иголке [9]. Ограничимся цитатой из соответствующей статьи. «Задача об иголке состоит в определении минимальной площади фигуры на плоскости, в которой единичный отрезок, «иглу», можно развернуть на 180 градусов, вернув его в исходное положение с обращённой ориентацией. Такое возможно проделать в круге радиуса 1/2. Другой пример - фигура, ограниченная дельтоидой... Оказывается, что можно построить фигуру с произвольно малой площадью».

Вернёмся к доказательству последней теоремы. Очевидно, что упоминаемая там точка N, лежащая на свободной окружности, является серединой диаметра кривой Штейнера. Таким образом, середина диаметров кривой Штейнера вычерчивает свободную окружность.

Возникает вопрос, какие кривые вычерчивают другие точки, делящие диаметр в постоянном отношении. Мы можем с большой вероятностью успеха предположить, что речь идёт о гипотрохоидах, связанных с кривой Штейнера. К тому же нам желательно рассмотреть их внешний вид и изучить те особенности, которыми они обладают.

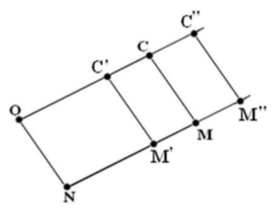
Снова вернёмся к доказательству последней теоремы. Для построения кривой Штейнера используется параллелограмм OCMN (см. теорему 28).

Если выбрать на отрезке точку М', которая делит отрезок ММ1, а, значит, и отрезок MN, в заданном отношении M'N/MN<1, то параллелограмм OC'M'N позволит построить удлинённую гипотрохоиду. В случае M''N/MN>1 параллелограмм OC''M''N позволит построить укороченную гипотрохоиду. При этом способе построения укороченные гипотрохоиды будут целиком охватывать кривую Штейнера, удлинённые будут расположены в её внутренней части.

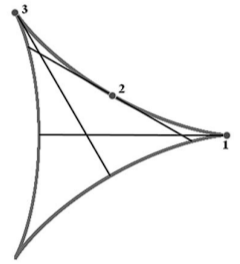
Более того, рассмотрим качение диаметра по одной из арок кривой Штейнера. Нас интересует положение точки касания в различных фазах движения. В начальной фазе точка касания находится на правом конце отрезка (фаза 1). Далее она постепенно перемещается вдоль катящегося отрезка (фаза 2), пока не достигнет левого конца (фаза 3).

Таким образом, точка касания проходит вдоль всего отрезка и делит его во всех возможных отношениях. По этой причине любая удлинённая гипотрохоида, определяемая фиксированным отношением v = M'N/MN<1, касается каждой арки кривой Штейнера. На самом деле при полном цикле проката диаметра по кривой Штейнера он меняет ориентацию и касается каждой арки кривой ещё раз в точках, определяемых отношением 1 - v. Из этого следует, что удлинённая гипотрохоида похожа на листок клевера, но является кривой с самопересечениями.

Продемонстрируем наши рассуждения с помощью программы.

Отметим, что возникшее семейство кривых можно трактовать как гомотопическое преобразование кривой Штейнера в себя. При этом траекториями точек служат диаметры этой кривой, а фазами преобразования являются удлинённые гипотрохоиды, одной из которых является «тройная» окружность. Это преобразование, конечно, можно распространить и на укороченные гипотрохоиды.

Теперь изучим вопрос о форме подэр (напомним, что подэра - это геометрическое место оснований перпендикуляров, опущенных из точки на касательные к заданной кривой».) кривой Штейнера относительно произвольных точек плоскости. Начнём мы, однако, с внутренних точек кривой Штейнера.

Важными фактами, связанными с рассматриваемым вопросом, является то, что через любую внутреннюю точку области, ограниченной кривой Штейнера, можно провести

• три касательные к кривой Штейнера;

• три нормали к кривой Штейнера.

Продемонстрируем правильность этих утверждений с помощью рассуждений качественного характера. Три диаметра кривой Штейнера АА1, ВВ1 и СС1, исходящие из делят внутреннюю область на криволинейные треугольники. В частности можно говорить о треугольниках АА1В и АА1С, ВВ1А и ВВ1С, СС1А и СС1В. Назовём их базовыми.

Ещё раз рассмотрим процесс перекатывания диаметра по арке кривой Штейнера из положения АА1 в положение ВВ1. Обозначим концы движущегося диаметра через Т и Р. Тогда Т непрерывно переходит из положения А1 в положение В, а Р - из положения А в В1. Кроме того точка касания диаметра М переходит по арке из положения А в положение В.

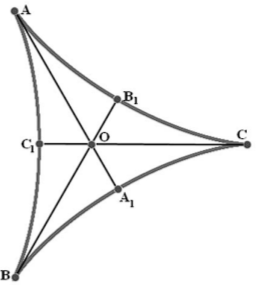
Своеобразная трансверсаль МТ при движении целиком заметает криволинейный треугольник АА1В, а трансверсаль МР - криволинейный треугольник АВ1В. Иными словами через каждую точку криволинейного треугольника АА1В можно провести касательную к арке АВ кривой Штейнера. Через каждую точку криволинейного треугольника АВ1В также можно провести касательную к арке АВ, которая отличается от предыдущей касательной.

Итак, с каждым базовым треугольником связана касательная к одной из арок кривой Штейнера. Кроме того, каждая точка внутри дельтоиды накрыта тремя базовыми треугольниками, поскольку любая пара треугольников с общим диаметром накрывает соответствующую область, но точка может попасть только в один треугольник из пары. В итоге становится ясно, что через любую внутреннюю точку области, ограниченной кривой Штейнера, можно провести три касательные к кривой Штейнера.

Отметим, что в общем положении две касательные проведены к одной арке, и одна - к другой. К третьей арке касательную провести нельзя.

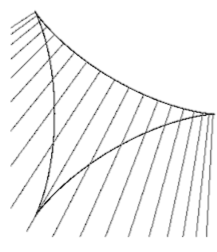
Перейдём к случаю нормалей. Здесь всё очень просто. Если двигать нормаль по одной из арок дельтоиды, то она, перемещаясь непрерывно, заметёт все внутренние точки соответствующей области без перекрытий. Таким образом, из каждой внутренней точки можно провести одну нормаль к каждой из трёх арок кривой Штейнера.

Теперь мы можем представить себе, как выглядит подэра кривой Штейнера относительно внутренней точки. Три касательные, проходящие через эту точку, обеспечивают тройное прохождение через неё подэры. Три нормали, проходящие через эту же точку, обеспечивают троекратное касание подэры и кривой Штейнера. Таким образом, можно предположить, что подэра кривой Штейнера похожа на деформированную трёхлепестковую розу Гранди (уравнение в полярных координатах р = a*sin3φ).

Чтобы в полной мере убедиться в этом построим подэры кривой Штейнера на экране. Для этого сначала проведём несложные вычисления, основанные на теореме 21. Пусть точка (xs; ys) сдвинулась вдоль окружности радиуса r0 с центром (x0; y0) на угол u. Прямая, проходящая через эту точку, повернулась на угол -u/2. Значит, направляющий единичный вектор этой прямой имеет координаты (cos(-u/2) ; sin(-u/2)), а прямая (касательная к кривой Штейнера) имеет уравнение q(x - xs) = p(y - ys) или qx - py = qxs - pys = c1.

Прямая, проходящая через произвольную точку (xt; yt), перпендикулярно касательной имеет уравнение p(x - xt ) = -q(y - yt ) или px + qy = pxt + qyt = c2. Соответствующая система уравнений всегда имеет решение, которое можно найти по правилу Крамера:

Теперь мы можем написать программу и построить подэры кривой Штейнера относительно различных точек. Эти же уравнения, задающие подэру параметрически, позволяют получить и её алгебраическое уравнение, поскольку она является алгебраической кривой. 

Теперь мы, наконец, переходим к геометрии треугольника.

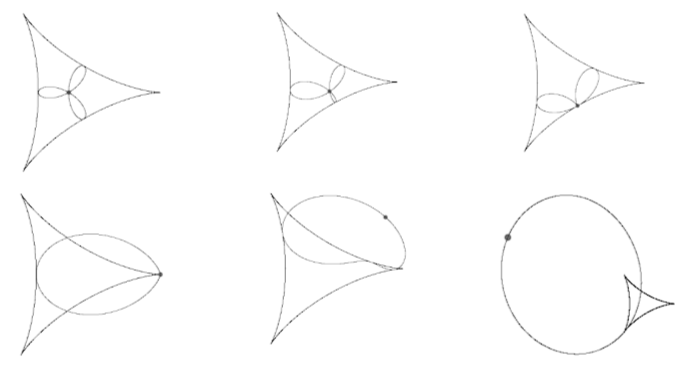
Теперь мы, наконец, переходим к геометрии треугольника.

11. НЕКОТОРЫЕ СВЕДЕНИЯ ИЗ ГЕОМЕТРИИ ТРЕУГОЛЬНИКА

Согласно Большой Советской Энциклопедии «треугольник прямолинейный, часть плоскости, ограниченная тремя отрезками прямых (стороны треугольника), имеющими попарно по одному общему концу (вершины треугольника)». Уже это определение показывает, что можно понимать термин «треугольник» по-разному. Данное определение аналогично определению круга, поскольку оно объединяет границу фигуры и внутреннюю область. Но можно понимать термин «треугольник» по аналогии с окружностью, акцентируя внимание на сторонах треугольника.

Что же касается сторон треугольника, то можно, как это делалось выше, называть сторонами треугольника отрезки, а можно и прямые, на которых эти отрезки лежат. В этом случае при обращении к методу координат появляется ещё одна точка зрения на треугольник. Каждая из сторон треугольника описывается линейной формой Li = aix + biy + ci, которая приравнивается к нулю. Произведение всех трёх линейных форм L1*L2*L3, приравненное к нулю, описывает совокупность всех сторон треугольника, то есть треугольник как таковой. И в данном контексте треугольник может рассматриваться как частный случай кривой третьего порядка. Более того, совокупность уравнений вида L1-L2-L3 = const порождает семейство кривых того же порядка, о котором можно сказать, что оно связано с данным треугольником. И это сразу указывает на то, что треугольник, ой, как не прост.

Однако далее мы будем придерживаться, условно говоря, школьной точки зрения на треугольник. Здесь философская рефлексия неуместна. Достаточно иметь перед собой привычный образ той геометрической фигуры, у которой есть три вершины, три угла и три стороны. При этом каждой вершине треугольника соответствует противоположная сторона.

Кроме того, с любым треугольником связаны следующие линии (по три линии каждого типа), почти всегда связывающие вершины с противоположными сторонами.

1. Медианы - отрезки, соединяющие вершины треугольника с серединами противоположных сторон. Три медианы треугольника пересекаются в одной точке называемой центроидом, которая является центром тяжести треугольника. Мы будем обозначать её буквой G.

2. Высоты - перпендикуляры, опущенные из вершин треугольника на противоположные стороны. Три высоты треугольника пересекаются в одной точке. Мы будем обозначать её буквой Н и называть ортоцентром.

3. Биссектрисы трёх углов треугольника пересекаются в одной точке, которая является центром вписанной окружности. Мы будем обозначать эту точку буквой I.

4. Срединные перпендикуляры к сторонам треугольника (именно они не проходят через вершины) пересекаются в одной точке, которая является центром описанной окружности. Мы будем обозначать эту точку буквой О.

Теперь мы переходим к фактам, выходящим за пределы школьного курса планиметрии.

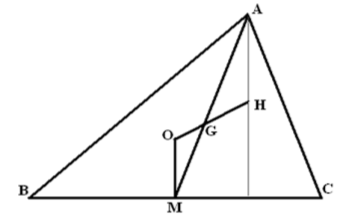
Прямая Эйлера. Три точки О, G и H лежат на одной прямой, называемой прямой Эйлера. Докажем этот факт, следуя [10]. На прямой OG выберем точку Н (пока мы о ней ничего достоверно не знаем, но обозначаем её так в надежде на будущее), которая удовлетворяет условию HG = 2*OG. Поскольку центроид делит медиану в том же отношении (AG = 2*MG), треугольники OGM и HGA подобны. Следовательно, отрезок АН параллелен отрезку ОМ. Таким образом, отрезок АН перпендикулярен стороне АВ, и точка Н лежит на высоте. Если провести аналогичные рассуждения и для двух других медиан, мы получим, что та же точка Н лежит на каждой из высот. Фактически мы доказали, что высоты треугольника пересекаются в одной точке, а точки О, G и H лежат на одной прямой.

Ортоцентр и описанная окружность. Те свойства ортоцентра, о которых мы сейчас расскажем, понадобятся нам в дальнейшем при доказательстве важных для нас теорем. Ортоцентр напрямую не связан с какими-либо окружностями. Тем не менее, оказывается, что окружность, симметричная относительно стороны треугольника описанной вокруг данного треугольника окружности, проходит через ортоцентр.

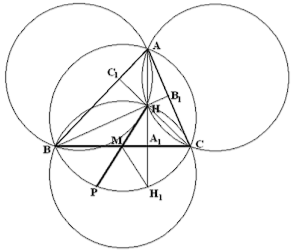
Более того, поскольку у треугольника три стороны, то и окружностей, симметричных относительно сторон, также три. И все они проходят через точку Н.

Действительно, угловая мера угла А треугольника АВС равна половине угловой меры дуги ВРС. Дополнительная к ней дуга ВНС имеет угловую меру 2п - 2 ∠ А. Но ∠ ВНС также равен меру 2п - 2 ∠ А, поскольку это угол между высотами треугольника АВС, опущенными на стороны угла А. Если симметрично отобразить описанную окружность относительно стороны ВС, то дуга ВРС перейдёт в дугу ВНС, а угол ВНС будет опираться на дугу с угловой мерой 2п - 2 ∠ А. Из этого следует, что точка Н лежит на любой из трёх симметричных окружностей.

Далее отметим, что симметрично отображённый относительно стороны ВС (и любой другой стороны треугольника) ортоцентр Н попадает в точку Н1, лежащую на описанной окружности. Наконец, очевидно, что фигура, состоящая из двух дуг ВНС и ВРС, обладает центральной симметрией относительно точки М, являющейся серединой стороны ВС. Из этого следует, что если продолжить отрезок НМ до пересечения с дугой ВРС, то точка М будет серединой отрезка НР.

Окружность Эйлера или окружность девяти точек. Середины трёх сторон треугольника, основания высот и середины отрезков, соединяющих вершины с ортоцентром, лежат на одной окружности.

Поскольку мы имеем дело с большим количеством точек, то будем широко использовать для их обозначения индексы: вершины треугольника обозначены через А1, А2 и А3. Середины сторон обозначены через G1, G2 и G3 (буква G выбрана, поскольку имеется связь этих точек с центроидом). Основания высот обозначены через Н1, Н2 и Н3. Середины отрезков, соединяющих вершины с ортоцентром обозначены через Т1, Т2 и Т3. Центр окружности Эйлера и её проекции на стороны обозначены через С, С1, С2 и С3. Наконец, точки пересечения описанной окружности с отрезками HG1, HG2 и HG3, о которых упоминалось выше, обозначены через Р1, Р2 и Р3.

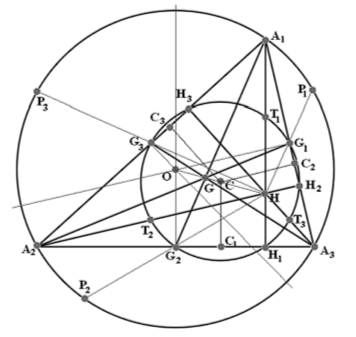
Доказательство теоремы об окружности Эйлера будет не длиннее описания обозначений. Подвергнем плоскость гомотетии с коэффициентом 1/2.

Тогда вершины треугольника А1, А2 и А3 перейдут в точки Т1, Т2 и Т3. Описанная же окружность перейдёт в окружность, проходящую через точки Т1, Т2 и Т3, ность Эйлера. Точки Р1, Р2 и Р3 перейдут в точки G1, G2 и G3, поскольку точка Gi является серединой отрезка HPí. Значит, окружность Эйлера проходит через середины сторон. Наконец, срединные перпендикуляры перейдут в прямые СС1, СС2 и СС3. При этом точки С1, С2 и С3 являются серединами отрезков H1G1, H2G2 и H3G3, ввиду чего точка С - центр окружности Эйлера, равноудалена и от середин сторон, и от оснований высот. Следовательно, окружность Эйлера проходит и через основания высот. Отметим ещё и тот факт, что центр окружности Эйлера лежит на прямой Эйлера.

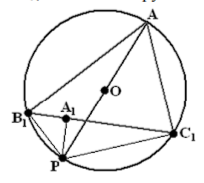
Прямые Симсона. Если выбрать на описанной окружности произвольную точку Р, то основания A1,B1 и C1 перпендикуляров, опущенных на стороны треугольника АВС лежат на одной прямой, называемой прямой Симсона. Каждой точке на описанной окружности соответствует своя прямая Симсона.

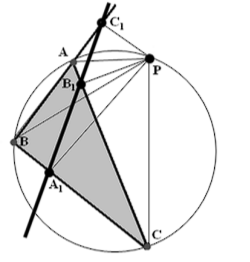
Задача состоит в том, чтобы доказать, что угол AB1C1 равен углу СВ1А1. Тем самым будет показано, что точки A1,B1 и C1 лежат на одной прямой. Рассмотрим четырехугольник AB1PC1. Вокруг него можно описать окружность. Значит углы AB1C1 и АРС1 опираются на общую дугу и равны между собой. Из точек A1 и B1 отрезок РС виден под прямым углом. Следовательно, эти четыре точки лежат на одной окружности. По этой причине углы A1B1C и A1PC, опирающиеся на одну дугу, равны. Если мы сумеем доказать, что угол АРС1 равен углу A1PC, то теорема будет доказана.

Углы при вершинах C1 и A1 четырехугольника BC1PA1 прямые, значит, углы при вершинах В и Р составляют в сумме развернутый угол, т.е. ∠C1PA1 = π - ∠ABA1. Углы АВС и АРС опираются на дополняющие друг друга дуги окружности, следовательно, они составляют в сумме развернутый угол, ∠ АРС = π - ∠ABA1. Итак, ∠C1PA1 = ∠ АРС. Теперь, вычитая из каждого из этих углов угол АРА1, получим углы АРС1 и А1РС. Таким образом, эти углы равны между собой. Теорема доказана.

Легко понять, что прямыми Симсона являются и высоты треугольника (точка Р совпадает с одной из вершин треугольника), и его стороны (точка P деаметрально противоположна одной из вершин треугольника).

Теорема Штейнера о прямых Симсона. Огибающей прямых Симсона является кривая Штейнера. Доказательство теоремы будет проведено по схеме, намеченной в книге [11], но более подробно. Отметим, что в указанной книге широко используются кинематические соображения, что в значительной степени соответствует стилю нашей статьи.

Кстати, по ходу доказательства будет передоказана предшествующая теорема о прямых Симсона, но уже кинематическим методом. Предваряя последующие рассуждения отметим, что прямые Симсона вращаются со скоростью -ω/2 вокруг точки, движущейся по окружности Эйлера со скоростью ω.

Но прежде чем приступать к доказательству основного результата, докажем небольшую лемму, имеющую кинематический смысл. Пусть две равных окружности у1 (нижняя) и Y2 (верхняя) пересекаются в точках Н и В, и пусть дуга НМ1В, как и аналогичная дуга окружности у2, имеет угловую меру а. Пусть прямые НМ1 и ВМ1 пересекаются с окружностью y2 в точках М2 и N соответственно. Тогда дуги М1В окружности у1 и М2В окружности y2 равны.

Действительно, поскольку угол НМ1В опирается на дугу с угловой мерой 2п - а, он равен п - a/2. Отсюда следует, что ∠ ВМ1М2 = a/2, так же как и ∠HM2B, который опирается на дугу окружности у2, имеющую угловую меру а. Из этого следует, что треугольник M2NM1 является равнобедренным, то есть хорды М1В и М2В равны между собой, как и стянутые ими дуги.

Кинематический же смысл леммы таков. Пусть исходя из точки В по окружности Y1 с угловой скоростью ю движется точка М1, а по окружности Y2 с угловой скоростью -ω движется точка М2. Тогда точки Н, М1 и М2 всегда находятся на одной прямой.

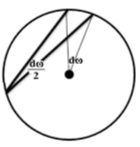
Отметим и ещё одну деталь. Хотя точка М1 движется с угловой скоростью ю, прямая НМ1 вращается с угловой скоростью -ω, поскольку угол, вписанный в окружность в два раза меньше центрального угла.

Перейдём к доказательству теоремы Штейнера. Пусть треугольник АВС вписан в окружность y, а по этой окружности с угловой скоростью ю движется точка М. Симметрично отразим окружность y относительно каждой из сторон нашего треугольника и получим три окружности Y1, Y2 и Y3, которые проходят че- »m-Mi-m, рез ортоцентр треугольника Н. Симметричные образы точки М, а именно М1, М2 и М3, будут двигаться по соответствующим окружностям с угловыми скоростями, равными -ω.

Если точка М совпадает с вершиной треугольника В, то очевидно, что точки М1 и М3 совпадают с этой вершиной, а точка М2 лежит на высоте, исходящей из В. Значит, точки Н, М1, М2 и М3 в данный момент лежат на одной прямой. По лемме точки Н, М1, и М3 так и будут оставаться на одной прямой при движении точки М.

Рассмотрев прохождение точки М через вершины А и С, мы убедимся, что все четыре точки Н, М1, М2 и М3 всегда будут располагаться на одной прямой, которая вращается вокруг ортоцентра с угловой скоростью -ω/2.

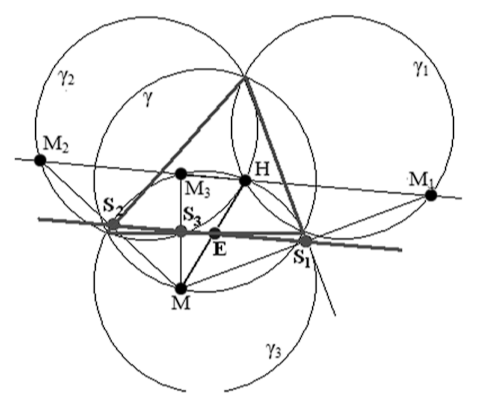
Считая основаниями треугольников стороны, параллельные прямой НМ1, рассмотрим теперь средние линии треугольников ММ1Н, МНМ3 и ММ3М2. Очевидно, что все они лежат на прямой, параллельной к НМ1. Следовательно, середины отрезков МН, ММ1, ММ2 и ММ3 лежат на одной прямой. Обозначим эти точки соответственно как E, S1, S2 и S3.

Очевидно, что точки S1, S2 и S3 являются основаниями перпендикуляров, опущенных из точки М на стороны треугольника АВС. Таким образом, мы повторно доказали, как и обещали, что эти точки задают прямую Симсона.

Теперь рассмотрим точку Е - середину отрезка МН. При гомотетичном преобразовании плоскости относительно ортоцентра с коэффициентом 1/2 точка М перейдёт в точку Е, которая, как мы уже знаем лежит на окружности Эйлера.

При движении точки М по описанной окружности с угловой скоростью ю точка Е движется по окружности Эйлера с тою же угловой скоростью. Через неё проходит прямая Симсона, параллельная прямой НМ1, вращающейся с угловой скоростью -ω/2. Таким образом, семейство прямых Симсона можно построить методом, описанным в теореме 21. При угловой скорости точки Е, равной ю, и угловой скорости вращения прямой Симсона, равной -ω/2, это семейство должно огибать кривую Штейнера, описанную вокруг окружности Эйлера. Теорема доказана.

12. ПОСТРОЕНИЕ ГРУППЫ ПРЕОБРАЗОВАНИЙ, СВЯЗАННОЙ С ГЕОМЕТРИЕЙ ТРЕУГОЛЬНИКА

Теорема Штейнера даёт возможность построить группу преобразований, которая, несомненно, имеет прямую связь с геометрией треугольника. Прежде чем строить её обсудим вопрос о связи треугольника и соответствующей ему кривой Штейнера. Итак, треугольник с помощью своих прямых Симсона порождает кривую Штейнера. Его стороны и высоты при этом являются касательными соответствующей кривой. Будем говорить, что данный треугольник вложен в кривую Штейнера.

Сейчас мы покажем, что в кривую Штейнера можно вложить треугольник любой формы, то есть треугольник подобный любому другому произвольно выбранному треугольнику. Вообще это обстоятельство почти очевидно, но мы в силу его важности для нас рассмотрим достаточно подробно.

Зафиксируем на плоскости окружность y и выберем два произвольных треугольника. Форма треугольника, которая у подобных треугольников одинакова, определяется двумя параметрами - двумя углами. Впишем в окружность y треугольники, подобные выбранным, и построим для каждого из них кривую Штейнера. Очевидно, что эти кривые будут конгруэнтны, поскольку равны их окружности Эйлера, вписанные в каждую из кривых Штейнера. Совместив две кривые Штейнера, мы вложим оба треугольника в одну дельтоиду. Можно провести эту процедуру практически, нарисовав соответствующие треугольники и кривые на двух кальках и наложив их друг на друга.

Однако подобные действия можно провести и с одним треугольником. Пусть на двух кальках нарисованы две кривые Штейнера, порождённые одинаковыми треугольниками. Ясно, что совместить кривые Штейнера на кальках можно несколькими способами. Число возможных вариантов равно шести, поскольку кривая Штейнера совмещается сама с собой либо при повороте на 120°, либо при зеркальной симметрии относительно касательной, проходящей через излом кривой.

Как истолковать это обстоятельство? Дело в том, что треугольник можно воспринимать не только как фигуру, подобную реальному предмету, но и более абстрактно, например, как упорядоченную тройку действительных чисел, задающую длины сторон. Тогда один треугольник со сторонами a, b и c превращается в шесть треугольников, а именно в {a, b, c }, {b, c, a }, {c, a, b }, -{a, b, c }, -{b, c, a }, -{c, a, b }, где знак минус указывает на смену ориентации треугольника на евклидовой плоскости. Подобное неоднозначное понимание треугольника можно усмотреть уже в одной из реконструкций доказательства Фалеса теоремы о равнобедренном треугольнике.

Сделаем следующее замечание по поводу описания треугольников, вложенных в кривую Штейнера. Построение кривой Штейнера по методу, описанному в теореме 21, мы обычно начинаем с того момента, когда точка, движущаяся по окружности находится на горизонтальном радиус-векторе, направленном вправо, а прямая, вращающаяся вокруг этой точки, горизонтальна. Естественно считать, что в этот начальный момент угол ω = 0. Далее радиус-вектор начинает вращаться против часовой стрелки, а прямая - по часовой. При этом положение каждой касательной к кривой Штейнера можно «проиндексировать» углом ю. В результате каждая может быть однозначно описана индексом. По этой причине мы можем сопоставить каждому треугольнику, вложенному в кривую Штейнера тройку действительных чисел, каждое из которых принадлежит отрезку [0; 2*п). На этот раз тройка является неупорядоченной.

Итак, кривая Штейнера содержит в себе треугольники всех форм. Естественно допустить, что группа преобразований, которую мы строим, будет связанна именно с кривой Штейнера. Продолжая построение группы, мы попытаемся сопоставить каждому треугольнику некоторую точку на плоскости.

Пусть некоторый треугольник вложен в кривую Штейнера. Тогда его ортоцентр лежит внутри области, ограниченной этой кривой, поскольку три касательных к кривой Штейнера можно провести только через внутренние точки. Этими касательными являются три высоты треугольника.

Теперь займёмся построением треугольника, ортоцентр которого является внутренней точкой области, ограниченной кривой Штейнера. Как мы знаем, диаметры кривой Штейнера, одновременно являющиеся касательными к ней, полностью заметают внутренность дельтоиды. По этой причине вместо того, чтобы выбирать произвольную точку Н внутри кривой Штейнера, мы выберем произвольный диаметр кривой Штейнера, лежащий на прямой L, касающейся этой кривой. Затем на этом диаметре выберем произвольную точку Н. Очевидно, что таким образом можно выбрать любую внутреннюю точку области, ограниченной кривой Штейнера.

Теперь наша задача состоит в том, чтобы построить треугольник, вложенный в кривую Штейнера, ортоцентр которого совпадает с точкой Н, а одна из высот - с проходящей через эту точку касательной L.

Мы знаем, что вписанная в кривую Штейнера окружность y является окружностью Эйлера искомого треугольника. Окружность y и касательная L обязательно имеют две общие точки U1 и U2, которые сливаются в одну только в том случае, когда диаметр касается окружности y. Это следует из метода построения кривой Штейнера, описанного в теореме 21.

Теперь подчеркнём два обстоятельства, которые нам нужно будет иметь в виду. Прежде всего, одна из двух упомянутых точек U2 является серединой диаметра кривой Штейнера. Кроме того, при качении диаметра вдоль окружности y точка пересечения касательных, проходящих через концы диаметра, пробегает по всей окружности y. Таким образом, через любую точку окружности y проходят две взаимно перпендикулярных касательных к кривой Штейнера.

Итак, на прямой L лежат две важные точки будущего треугольника. Одна из них должна стать основанием его высоты, а вторая - будет лежать посредине между ортоцентром и вершиной, из которой опущена высота L. Именно эта (вторая) роль будет предоставлена середине диаметра D1D2 точке U2.

Теперь мы можем описать процедуру построения искомого треугольника АВС. Поскольку нам известны ортоцентр Н и окружность Эйлера y с центром Z, мы можем гомотетией относительно Н с коэффициентом 2 получить окружность £, в которую будет вписан треугольник АВС.

Вершины В и С мы получим как точки пересечения перпендикуляра к диаметру D1D2 в точке U1 с окружностью Ç. Поясним, почему такое пересечение всегда имеет место. Крайними положениями ортоцентра Н являются концы диаметра D1 и D2. Гомотетические образы окружности Эйлера в свою очередь являются крайними положениями описанной окружности. Их центры F1 и F2 являются концами отрезка, параллельного диаметру D1D2 и имеющего такую же длину. По этой причине два крайних варианта описанных окружностей касаются и друг друга и перпендикуляра к диаметру, восстановленного из точки U1. Касание происходит в точке F3, диаметрально противоположной на окружности Эйлера середине диаметра точке U2. Все остальные описанные окружности, соответствующие промежуточным положениям ортоцентра Н на диаметре заведомо пересекаются с перпендикуляром U2U3.

Перейдём к построению третьей вершины треугольника. Вершина А является точкой пересечения прямой L с описанной окружностью. Однако, поскольку прямая и окружность пересекаются в двух точках, нужно разобраться, какую из них следует выбрать. Поскольку точка Н лежит на диаметре кривой Штейнера, то при гомотетии точки U1 и U2 переходят в точки пересечения прямой L с описанной окружностью Ç. Точкой А назовём гомотетический образ точки U2, а гомотетический образ точки U1 обозначим через Р.

Итак, треугольник построен. Однако нам необходимо доказать, что точка Н является его ортоцентром. Отметим то обстоятельство, что различные расположения точки Н относительно отрезка U1U2 создают различные конфигурации для искомого треугольника АВС. Однако доказательство того, что Н при данном способе построения является ортоцентром, не меняется. По этой причине мы приводим на чертеже две конфигурации (первая - Н правее отрезка U1U2; вторая - Н внутри отрезка U1U2), но доказательство проводим только для первого случая.

Поскольку точка U1 при гомотетии с центром в Н и коэффициентом 2 переходит в точку Р, отрезки HU1 и U1P равны. На прямой ВС выделим точку N, такую, чтобы отрезки ВU1 и U1N были равны. Треугольники ANB и СРН являются равнобедренными. Более того, половины их углов при вершине - углы РАВ и РСВ, опираются на дугу РВ, а, значит, равны между собой. Таким образом, треугольники ANB и СРН подобны.

Треугольник АНТ по этой причине является прямоугольным. Действительно, ∠ ВСН + ∠ АНТ = 90° как острые углы треугольника СН1Н. Кроме того, ∠ НАВ = ∠ ВСН. Следовательно, прямая АВ является высотой треугольника АНС. Но его высотой является и прямая СВ. Таким образом, точка В является ортоцентром треугольника АНС. По этой причине третьей высотой этого треугольника является прямая ВН. То есть прямая НВ перпендикулярна АС.

Но это означает, что в треугольнике АВС две высоты АР и НВ пересекаются в точке Н, и эта точка является ортоцентром треугольника АВС.

По поводу случая, когда диаметр касается окружности Y, и точки U1 и U2 сливаются, нет необходимости говорить много, поскольку доказательство существования треугольника полностью сохраняет свою силу. Ограничимся лишь тем, что приведём чертёж, соответствующий этому случаю. Отличие лишь в том, что угол АСВ опирается на дугу АВ, а угол ВАН является углом между касательной и хордой, а, значит, тоже равен половине той же дуги АВ.

Наконец, отметим, что в случаях, когда Н находится на самой кривой Штейнера, треугольник АВС вырождается в отрезок. Это обстоятельство вытекает из наших рассуждений, посвящённых доказательству пересечения перпендикуляра к диаметру D1D2, восстановленному из точки U1, с окружностью £.

Кроме всего прочего понятно, что поскольку одна из высот и одна из сторон треугольника АВС являются касательными к кривой Штейнера, то и все его стороны и высоты также являются касательными к ней. Это следует из того, что, кривая Штейнера, образованная прямыми Симсона треугольника АВС, должна совпадать с исходной кривой Штейнера.

Оформим доказанное нами свойство кривой Штейнера как теорему.

Теорема 31. Каждая точка, находящаяся внутри кривой Штейнера, является ортоцентром некоторого треугольника, высоты и стороны которого касаются данной кривой. Среди этих треугольников можно найти треугольник любой формы, то есть треугольник подобный любому произвольно выбранному треугольнику.

Опираясь на этот факт, можно построить группу преобразований, переводящую любой треугольник в любой другой.

Построение группы можно провести исходя из следующих соображений. С точки зрения топологии внутренние точки области, ограниченной кривой Штейнера, гомеоморфны внутренней части единичного круга, а для внутренности круга существует, тесно связанная с геометрией группа автоморфизмов.

Речь, естественно, идёт о группе дробно-линейных преобразований. Эта группа соответствует группе движений плоскости Лобачевского, реализованной в модели Пуанкаре. В первой части нашей статьи мы из других соображений отмечали возможную связь между геометрией треугольника и группой преобразований геометрии Лобачевского. Сейчас же мы со значительно большим основанием можем говорить о том, что группа дробно-линейных преобразований позволяет переводить любые треугольники евклидовой плоскости друг в друга.

Понятно, что мы рассматриваем единичный круг на комплексной плоскости. Выбранный нами гомеоморфизм сопоставляет каждому треугольнику комплексное число, по модулю меньшее единицы.

Действие группы дробно-линейных преобразований сохраняется при любом выборе этого гомеоморфизма между внутренними областями кривой Штейнера и единичного круга. Тем не менее, этот выбор влияет на восприятие множества евклидовых треугольников, поскольку при разных гомеоморфизмах множества треугольников различным образом группируются в совокупности, которые соответствуют таким фигурам геометрии Лобачевского, как прямые, окружности, орициклы и эквидистанты.

По-видимому, наиболее естественным гомеоморфизмом между внутренними точками кривой Штейнера и внутренностью круга в этом случае должно было бы стать конформное их отображение друг на друга. По теореме Римана такое отображение существует, но его построение является достаточно сложной задачей. По этой причине мы можем использовать рассмотренную нами выше неаналитическую функцию w = 2z + z². Однако в любом случае при нашем подходе преобразование треугольников друг в друга производится группой дробно-линейных преобразований.

В целом данный вопрос выходит за рамки нашей статьи, и по этой причине мы пока откладываем его рассмотрение. В то же время нам необходимо сделать определённые выводы.

Прежде всего, отметим, что теорема Штейнера и связанные с ней дополнительные построения позволяют утверждать, что каждый треугольник порождает на плоскости сложную структуру, содержащую точки, прямые, кривые и новые треугольники. При этом эта структура в определённом смысле содержит любой из возможных треугольников, то есть каждый треугольник в известном смысле уже содержит в себе всю геометрию треугольника.

Кроме того, достаточно естественной группой преобразований, действующей на этой структуре, является группа движений геометрии Лобачевского. Конечно, ничего особенно удивительного в этом обстоятельстве нет, поскольку геометрии Лобачевского имеет модель в рамках планиметрии Евклида. Как известно, эта модель эквивалентна модели Пуанкаре, но построена в чисто геометрическом духе, как геометрия окружностей.

Тем не менее, тот факт, что геометрию треугольника можно связать с группой иной, хотя и тесно связанной с евклидовой геометрией, является весьма значимым. Далее мы коснёмся ещё ряда вопросов, связанных с теоремой Штейнера и покажем ещё ряд, порождаемых ею объектов.

13. ОРТОПОЛ И КРИВАЯ ШТЕЙНЕРА

Прямую связь с нашей тематикой имеет также и такое малоизвестное понятие как ортопол. Термин включает в себя части слов «ортогональность» и «полюс». Обоснованность такого названия можно усмотреть в определении ортопола.

Пусть задан треугольник АВС и прямая L. Из вершин треугольника опустим на прямую L перпендикуляры и обозначим их основания через А1, В1 и С1 соответственно. Из точки А1 восстановим перпендикуляр к стороне ВС, из точки В1 - перпендикуляр к стороне АС, и, наконец, из точки С1 - перпендикуляр к стороне АВ. Тогда эти три перпендикуляра пересекутся в одной точке, называемой ортополом прямой L относительно треугольника АВС.

Ортопол упоминается в статье [12]. В частности там указано, что существование ортопола следует из теоремы Штейнера об ортологичных треугольниках. Эта теорема доказывается в книге [13]. В следующих двух абзацах приведём её формулировку и доказательство, почти дословно взяв его из [13] и не делая своих пояснений. При этом значение термина «ортологичность» треугольников соответствует ситуации, описанной в теореме.

Теорема Штейнера об ортологичности. Если перпендикуляры из вершин треугольника A1B1C1 на стороны треугольника ABC пересекаются в одной точке, то перпендикуляры из вершин треугольника АВС на стороны треугольника А1В1С1 пересекаются также в одной точке.

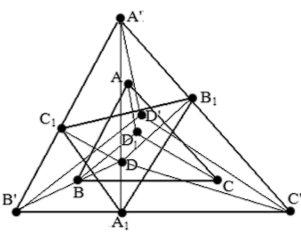
Положим, что перпендикуляры из вершин треугольника A1B1C1 на стороны треугольника ABC пересекаются в точке D. Проведя через А1, В1, С1 прямые, параллельные сторонам треугольника АВС получим треугольник A'B'C' - пусть D' есть, точка изогонально сопряженная с точкой D относительно этого треугольника. Так как треугольник A1B1C1 есть подэрный треугольник точки D относительно A'B'C', то прямые A'D', B'D' и C'D' перпендикулярны к сторонам его; но треугольники АВС и A'B'C' гомотетичны; поэтому перпендикуляры из A, B и C на стороны треугольника А1В1С1 как прямые соответственные с A'D', B'D' и C'D', пересекаются в одной точке D'.

К сожалению, мы не имеем возможности говорить о подэрных (в современной терминологии - педальных) треугольниках и изогональном сопряжении точек. Ограничимся тем, что процитируем рассуждение из [12] выводящее теорему об ортополе из теоремы Штейнера:

«В случае ортопола проекции вершин треугольника АВС на прямую L - точки А1, В1, С1 - можно считать вершинами вырожденного треугольника, а параллельные перпендикуляры - пересекающимися в бесконечно удалённой точке».

Теперь объясним, по какой причине мы начали разговор об ортополе. Прежде всего, отметим, что в определении ортопола и прямых Симсона есть нечто общее, но, так сказать, с точностью до наоборот. В одном случае проведение перпендикуляров к сторонам треугольника позволяет получить точку, в другом - прямую. Эта ассоциация, естественно, могла бы оказаться случайной, но между ортополом и прямыми Симсона существует вполне реальная связь.

Рассмотрим совокупность точек ортопола семейства параллельных прямых. Легко понять, что она образует прямую, перпендикулярную ко всем прямым семейства. И, оказывается, эта прямая является одной из прямых Симсона.

Поскольку мы решили обойтись без использования понятия об изогональном сопряжении точек, мы дадим другое доказательство теоремы об ортополе, дополненной последним утверждением предыдущего абзаца.

При этом мы всё же используем ещё одно понятие элементарной геометрии, речь идёт о радикальной оси двух окружностей [14].

В школьном курсе геометрии доказывается следующая теорема: пусть две прямые l1 и l2 проходят через точку М и пересекают окружность s в точках А1, В1 и А2, В2 соответственно, тогда произведение длин отрезков МА1-МВ1 равно произведению МА2-МВ2. Тем самым, указанное произведение не зависит от выбора прямой, проходящей через точку М. Его называют степенью точки М относительно окружности s. Если считать отрезки МА и МВ направленными, то степень точки приобретает знак. Для точек, лежащих внутри окружности, она будет отрицательной, а для точек вне окружности - положительной.

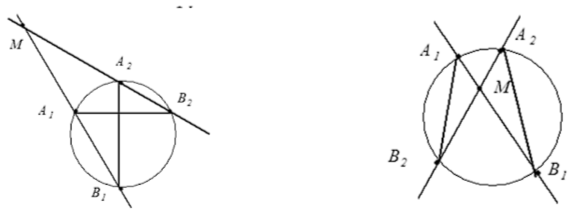
Теорема о радикальной оси. Пусть на плоскости заданы две неконцентрических окружности, тогда геометрическое место точек плоскости, имеющих равные степени относительно каждой из окружностей, является прямой линией, перпендикулярной линии центров данных окружностей. Эту прямую называют радикальной осью двух окружностей.

Доказательство. Выберем систему координат на плоскости так, чтобы ее начало совпадало с центром одной из окружностей, а ось абсцисс совпадала с линией центров.

Используя координаты точек, приведенные на чертеже, получаем, что МО1² = 1₁² = x² + y² и МО₂² = I₂² = (x - a)² + y². Легко понять, что степени точки М относительно этих окружностей соответственно равны S₁ = l₁² - r₁² = x² + y² - r₁² и S₂= I₂² — r₂² = (x — a)² + y² - r₂². Приравнивая эти выражения, получаем алгебраическое уравнение x² + y² - r₁² = (x - a)² + y² - r₂². После раскрытия скобок, квадраты координат х и у сокращаются. Более того, координата у исчезает из уравнения совсем. Таким образом, х является постоянной величиной x = (a²+r₁²-r₂²)/2*a. Перед нами ни что иное, как уравнение вертикальной прямой на координатной плоскости. Итак, радикальная ось является прямой, которая перпендикулярна оси х, то есть линии центров двух окружностей.

Из доказанной теоремы следует, что радикальная ось двух пересекающихся окружностей проходит через точки пересечения этих окружностей, поскольку они имеют нулевые степени.

Теорема об ортополе. Пусть на плоскости заданы треугольник АВС и прямая L. Из вершин треугольника опустим на прямую L перпендикуляры и обозначим их основания через R, Q и P соответственно. Из точки R восстановим перпендикуляр к стороне ВС, из точки Q — перпендикуляр к стороне АС, и, наконец, из точки P — перпендикуляр к стороне АВ. Тогда эти три перпендикуляра пересекутся в одной точке, называемой ортополом прямой L относительно треугольника АВС.

Доказательство (с использованием традиционных понятий евклидовой планиметрии). Мы уже говорили о том, что если существует точка ортопола некоторой прямой L на плоскости, то точки ортопола существуют и у всех параллельных L прямых. По этой причине теорему об ортополе достаточно доказать для всех прямых, проходящих через некоторую точку плоскости, например, через вершину А треугольника АВС. В этом случае точка R, упомянутая в формулировке теоремы, будет совпадать с точкой А для всех прямых пучка с центром в точке А.

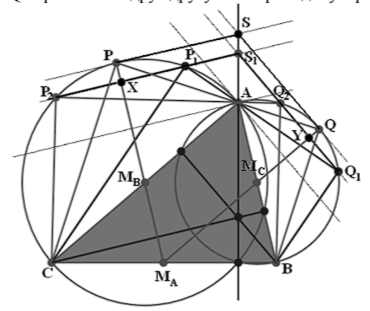
Пусть точки МА, МВ и МС - середины сторон треугольника АВС. На сторонах АВ и АС как на диаметрах построим окружности yB и УС. Затем проведём две средние линии треугольника АВС - МАМВ и МАМС. Они параллельны сторонам АВ и АС соответственно. Пусть Р и Q точки их пересечения с окружностями yC и уВ, лежащие в одной полуплоскости с вершиной А относительно прямой ВС.

Пусть стороны АВ, ВС и СА имеют длины c, a и b соответственно. Длина отрезка МАМВ равна с/2, МВР = b/2, МАМС = b/2 и MCQ = с/2. Таким образом, МАР = MAQ, то есть треугольник МAРQ является равнобедренным.

Углы РМAQ, РМВА и AМСQ равны между собой, как углы с соответственно параллельными сторонами. Следовательно, углы при основании равнобедренных треугольников МAРQ, МВРА и МСAQ также равны. Из этого вытекает, что прямые PQ, РА и AQ совпадают между собой. Значит, отрезок PQ проходит через точку А.

Далее поскольку треугольники СРА и BQA являются прямоугольными, прямые СР и BQ параллельны друг другу как перпендикуляры к прямой PQ.

Проведём через точку P касательную к окружности уС, а через точку Q касательную к окружности уВ. Обозначим точку их пересечения через S. Прямоугольные треугольники МAРS и MAQS имеют общую гипотенузу МА8 и по равному катету МАР и MAQ. Следовательно, они равны, как равны и их катеты РS и QS. Степень точки S относительно окружности yC равна РS2, а степень точки S относительно окружности YB равна QS2, то есть эти степени равны, и точка S лежит на радикальной оси окружностей yC и уВ. Но очевидно, что эта ось совпадает с высотой треугольника АВС, опущенной из вершины А.

Теперь легко понять, что точка S является точкой ортопола прямой PQ относительно треугольника АВС. И для этой прямой доказано, что точка ортопола существует. Перейдём к доказательству существования ортопола для других прямых пучка с центром в точке А.

Проведём произвольную хорду Р1Р2 окружности уС, перпендикулярную прямой РМА, проходящей через центр уС. Очевидно, что дуги Р1Р и Р2Р равны. Проведём прямую Р1А до пересечения с окружностью YB в точке Q1 и прямую Р2А до пересечения с окружностью YВ в точке Q2. Поскольку равные вертикальные углы РАР1 и QAQ1 опираются на дуги РР1 и QQ1, то эти дуги имеют равные угловые меры, так же как и дуги РР2 и QQ2. Значит, дуги QQ1 и QQ2 равны. По этой причине прямая Q1Q2 перпендикулярна к прямой МАQ.

Кроме того, прямые ВР1 и CQ1 параллельны, так как образуют с параллельными прямыми ВР и CQ равные углы. Одновременно прямые ВР1 и CQ1 перпендикулярны к прямой Р^1. По той же причине прямые ВР2 и CQ2 параллельны между собой и перпендикулярны к прямой P2Q2.

Пусть точка S1 является точкой пересечения прямых Р^1 и ₽2Q2. Если она лежит на прямой As - высоте треугольника АВС, то она представляет собой ортопол сразу двух прямых, Р1Q1 и Р2Q2.

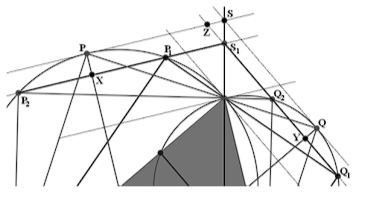
Обозначим угол РМВР1 через ф, а углы треугольника АВС через а, ß и y соответственно. Далее, пусть точки Х и Y являются серединами хорд Р1Р2 и Q1Q2 соответственно. Тогда длина отрезка РХ равна b/2(1 - cosφ), а длина отрезка QY равна c/2(1-cosφ)

Обозначим точку пересечения прямых Р1Р2 и AS через Si. Через точку S1 проведём прямую параллельную прямой PS. В результате возникнет треугольник SS1Z. Поскольку его стороны перпендикулярны сторонам треугольника АВС, угол SZS1 равен а, угол ZSS1 равен ß и угол SS1Z равен y. В предыдущем абзаце мы фактически установили, что высота h1 этого треугольника, опущенная из вершины S1 равна b/2(1 - cosф). Обозначим высоту через h2 высоту, опущенную из вершины S. Вычислим её длину.

Пусть k - коэффициент подобия треугольников АВС и ZSS1 (k = АВ : ZS). Тогда удвоенная площадь треугольника АВС может быть выражена двумя способами: с*k*h1 = b*k*h2. Отсюда следует, что h2 = (c*h1)/b = c/2*(1-cosф) Но, как мы видели, это длина отрезка YQ. Значит, прямая, проходящая через точку S1 параллельно прямой SQ, удалена от неё на такое же расстояние, как и прямая Q1Q2. Эти прямые совпадают, и, следовательно, прямые Р1Р2 и Q1Q2 пересекаются в точке S1, лежащей на прямой AS. Итак, теорема об ортополе доказана с помощью традиционных понятий евклидовой планиметрии.

Теорема 32. Пусть на плоскости заданы треугольник АВС и прямая L. При этом прямая L1, проходящая через точку ортопола перпендикулярно прямой L, является прямой Симсона треугольника АВС.

Доказательство. Чтобы сделать доказательство более обозримым начнём с напоминания простых фактов школьной геометрии и на их основе проведём простые вычисления. Кроме того, ещё раз вспомним о принятых нами в предыдущем доказательстве обозначениях.

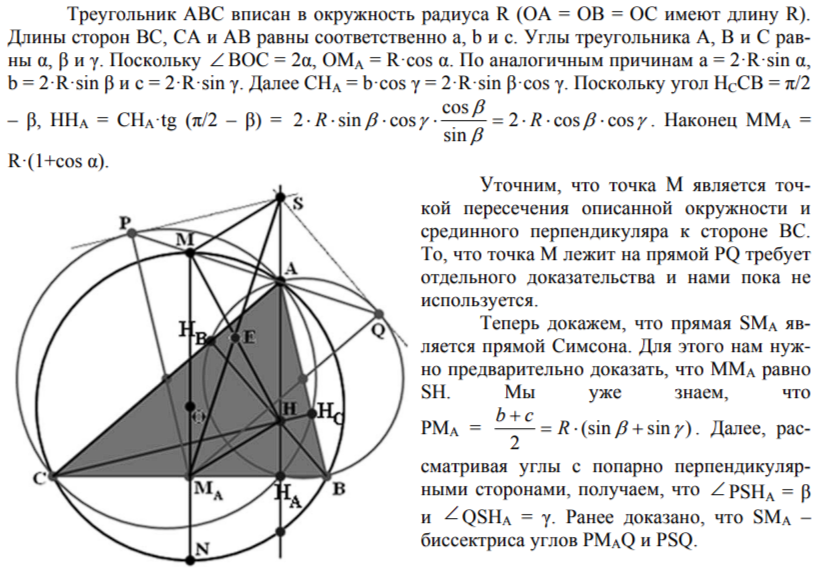
Из этого следует, что четырёхугольник MSHMA является параллелограммом. Его диагонали МН и SMA в точке пересечения Е делятся пополам. Из доказательства теоремы об огибающей прямых Симсона следует, что точка Е лежит на окружности Эйлера.

Далее, дуга описанной окружности NB имеет угловую меру а, а дуга ВА - угловую меру 2у. Отсюда вытекает, что дуга АМ имеет угловую меру п - а - 2y = ß - Y.

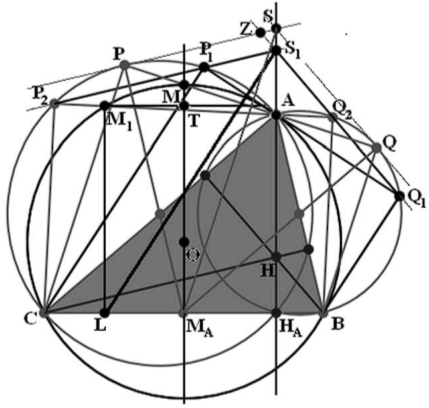
Пусть точка М двигается по описанной окружности и служит для построения прямых Симсона. Когда она совпадает с вершиной А, прямой Симсона является высота SH треугольника АВС. После смещения точки М против часовой стрелки на угол ß-y соответствующая ей прямая Симсона будет проходить через точку Е и отклонится от высоты SH по часовой стрелке на угол (ß-y)/2. Но именно в таком положении и находится прямая SMA. Значит, эта прямая является прямой Симсона треугольника АВС.

В общем случае мы будем рассуждать сходным образом, но отклонение прямых Симсона (S1L) будем отсчитывать от прямой SMA.

Вернёмся к нашему доказательству теоремы об ортополе. Если дуга РР1 окружности Ye имеет угловую меру ф, то прямая P1S1 отстоит от параллельной прямой PS на расстояние b/2*(1-cosф). Треугольник ZSS1 подобен треугольнику АВС с коэффициентом подобия k, который мы пока ещё не вычисляли. Точка S1 является точкой ортопола прямой P1Q1, проходящей через вершину А. Прямая S1L, перпендикулярная P1Q1 является геометрическим местом точек ортопола, прямых параллельных прямой P1Q1. Поскольку угол Р1АР опирается на дугу РР1 он равен ф/2, то есть прямые PQ и P1Q1 пересекаются под этим углом, как и перпендикулярные им прямые SMA и S1L. Отметим также, что угол LS1H равен (ß-y)/2+ф/2.

Вычислим коэффициент подобия треугольников АВС и ZSS1 (k = АВ : ZS), а затем длину отрезка SS1. Высоте треугольника ZSS1, опущенной из вершины S1 и имеющей длину b/2*(1-cosф), соответствует высота треугольника АВС, опущенная из вершины С и имеющая длину b*sin а. Таким образом,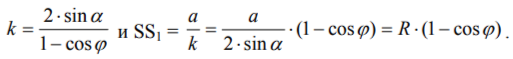

Пусть М1 - такая точка на описанной окружности, что M1L является перпендикуляром к стороне ВС. Если бы угловая мера дуги ММ1 равнялась ф, и отрезок M1L равнялся бы отрезку S1H, то работала бы логика, ранее применённая нами к прямой SMA. А именно, четырёхугольник М1LHS1 является параллелограммом, точка пересечения его медиан лежит на окружности Эйлера и наклон прямой S1L соответствует наклону прямой Симсона, связанной с точкой М1.

Итак, чтобы быть прямой Симсона, прямая S1L должна удовлетворять четырём свойствам:

1. Угол LS1H равен (ß-y)/2+ф/2.

2. Угловая мера дуги ММ1 равна ф.

3. Длина отрезка M1L равна длине отрезка S1H.

4. Длина отрезка SS1 равна R*(1 - cos ф).

Покажем, что прямую удовлетворяющую свойствам 2 - 4 можно легко построить, а затем покажем, что для неё выполняется и свойство 1. Приступим к построению. Положение точки S1 уже определено (свойство 4). При этом отрезок S1H короче отрезка SH на R*(1 - cos ф).

Положение точки М1 определяется свойством 2: угловая мера дуги ММ1 равна ф. Это значит, что угол МОМ1 равен ф, из чего следует, что длина отрезка МТ равна R*(1 - cos ф). Но это как раз и означает, что отрезок M1L короче отрезка ММА тоже на R*(1 - cos ф). И поскольку ММА = SH, то M1L = S1H. Свойство 3 таким образом выполняется.

Перейдём к проверке свойства 1. Сначала отметим, что MAL = R*sin ф. Теперь мы можем указать длины катетов прямоугольного треугольника S1HAL.

Теорема 33. Пусть вокруг треугольника описана окружность. Множество точек ортополов касательных к ней относительно этого треугольника образуют кривую Штейнера.

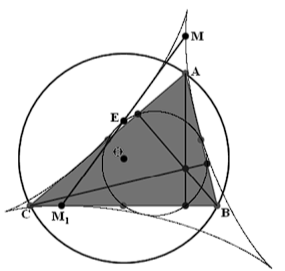
Доказательство. Мы доказали, что каждая из прямых Симсона образована точками ортопола семейства параллельных прямых. По этой причине, диаметры ММ1 кривой Штейнера, связанной с треугольником АВС лежат на таких прямых. И именно концы этих диаметров вычерчивают эту кривую. Точка Е, лежащая на окружности Эйлера и являющаяся серединой диаметра, одновременно является серединой отрезка LS1 (в обозначениях, принятых в предыдущем доказательстве). Чтобы доказать нашу теорему достаточно показать, что точка М является ортополом прямой, касающейся описанной окружности и параллельной прямой P1Q1.

Из этой теоремы вытекает следующий факт. Если мы берём любую окружность, концентрическую к описанной, то все ортополы всех её касательных сдвинуты относительно ортополов касательных к описанной окружности на постоянную длину. Из-за этого они делят диаметры кривой Штейнера в постоянном отношении, а, значит, вычерчивают гипотрохоиду, связанную с кривой Штейнера.

В результате можно построить отображение плоскости на себя (не взаимно однозначное) следующим образом. Каждая точка плоскости лежит на единственной окружности, входящей в семейство концентрических окружностей с центром О Кроме того, каждая прямая на плоскости касается единственной окружности, принадлежащей семейству концентрических окружностей с центром О (её радиус равен расстоянию от точки О до этой прямой). Таким образом, каждой точке на плоскости может быть поставлена единственная прямая, касающаяся в этой точке одной из концентрических окружностей.

Наше отображение, порождаемое треугольником АВС, будет переводить произвольную точку Т плоскости (кроме точки О, в которой отображение не определено) в ортопол прямой, проходящей через точку Т перпендикулярно прямой ОТ, относительно треугольника АВС. При этом каждая из концентрических окружностей будет переходить в гипотрохоиду. В результате мы можем рассматривать треугольник АВС как некую динамическую структуру, порождающую достаточно сложное преобразование плоскости. Естественно, что существуют и отображения порождаемые треугольником по иным принципам, например, изогональные и изотомические отображения [15]. Мы же хотим раз показать, что треугольник порождает структуры имеющие дифференциально-геометрический характер.

Продемонстрируем действие нашего отображения с помощью программы.

Сделаем ещё ряд замечаний по поводу ортопола и его связи с прямыми Симсона. Прежде всего, ортопол является понятием, которое как бы делает треугольник источником своеобразного силового поля, которое «дотягивается» до любой прямой и порождает соответствующую этой прямой точку. Именно по этой причине и появляется возможность построить наше отображение.

Далее, теорема Штейнера о прямых Симсона, уже сама по себе позволяет построить гипотрохоиды, связанные с кривой Штейнера. Однако использование ортопола придаёт гипотрохоидам более весомую связь с треугольником. Каждая из них становится образом некоторой окружности, связанной с треугольником. При этом каждая точка гипотрохоиды является точкой ортопола, то есть связана с треугольником напрямую.

Наше отображение не определено в точке О по следующей причине. Нельзя выделить одну прямую из пучка прямых с центром в точке О. Из-за этого точку О приходится рассматривать как окружность нулевого радиуса, с которой соприкасаются все прямые упомянутого пучка. Поскольку, как легко понять, соответствующая точка ортопола совпадает с серединой диаметра кривой Штейнера, то окружность нулевого радиуса отображается (в том числе и нашей программой) в окружность Эйлера.

Естественно, что таким же образом, то есть как окружность нулевого радиуса, можно рассматривать и любую точку на плоскости. Таким образом, после выбора треугольника каждой точке Т на плоскости ставится в соответствие кривая, образованная точками ортопола пучка прямых с центром Т. На рисунке изображены две таких кривых для двух точек плоскости.

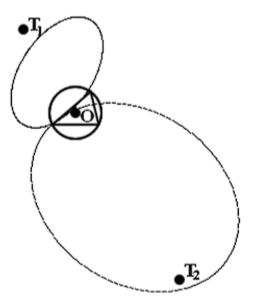
Отметим, что при произвольном выборе двух точек плоскости соответствующие им кривые обязательно пересекаются в точке ортопола соединяющих их прямой.

Наконец, наше отображение следующим образом позволяет преобразовывать одну гладкую кривую в другую. Пусть точка Т лежит на исходной кривой. Проводим в этой точке касательную и строим её орторол S.

Тогда множество точек S образует некоторую кривую, которая является образом исходной кривой. Интересно, что любая прямая линия при подобной процедуре преобразуется в точку. На рисунках показаны образы сдвигаемых по вертикали парабол, оси симметрии которых проходят через центр описанной окружности.

Построенные нами кривые являются порождением парабол, которые не связаны с треугольником. Естественно полагать, что больший интерес представляет преобразование кривых, связанных с треугольником, например, эллипса Штейнера. Отметим, что имеются в наличии и параболы, непосредственно связанные с треугольником. Например, такая парабола возникнет, если вершину А рассматривать в качестве фокуса, а сторону ВС в качестве директрисы.

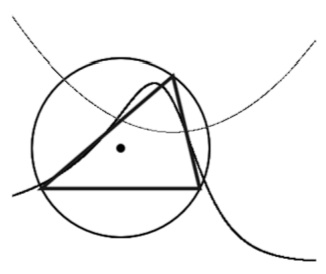
Ясно также, что характер нашего отображения несколько меняется в зависимости от формы треугольника. Например, если треугольник правильный, достигается большая симметрия между кривыми, расположенными в различных частях плоскости.

Преобразование кривых с помощью ортопола можно применить, в том числе, и к самой кривой Штейнера. Результат преобразования для случая правильного треугольника показан на чертеже.

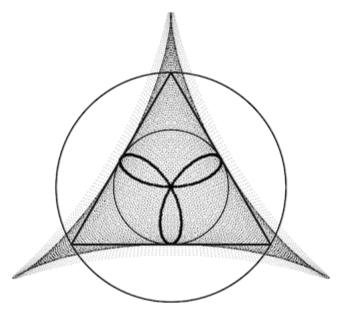
Мы уже не имеем возможности обсуждать вопросы, связанные с ортополом и основанным на нём отображением плоскости. В том числе даже и вопросы, возникающие при взгляде на приведённые нами чертежи, например, являются ли образы точек на основе пучков с центрами в этих точках эллипсами. Или на вопрос о том, всегда ли образ кривой Штейнера при нашем отображении является её подерой.

Вопросы, связанные с понятием ортопола, мы рассмотрели чтобы лишний раз показать, насколько широкой является проблематика, связанная с геометрией треугольника. Рассмотрение не прояснённых нами моментов предоставляем читателю.

14. НЕКОТОРЫЕ ДОПОЛНИТЕЛЬНЫЕ ВОПРОСЫ

Данная статья из-за её значительного объёма требует завершения, однако, остаётся целый ряд вопросов, которые связаны с изложенным выше подходом к геометрии треугольника. Прежде всего, возникает вопрос о связи данного подхода с общим состоянием современной геометрии треугольника. Как мы говорили, геометрия треугольника является теорией, обладающей огромным количеством результатов. Однако эти результаты пока не складываются в единую картину. Предлагаемая нами точка зрения, возможно, является одним из вариантов нащупывания общего подхода к геометрии треугольника, насколько такой подход возможен. В любом случае поиск в этом направлении необходим.

Чтобы оценить сложность задачи достаточно ознакомиться, например, с работами [15-20], причём этот список всего на всего может послужить исходным пунктом изучения геометрии треугольника. В нашей же статье остались незатронутыми даже такие исходные объекты геометрии треугольника, как вписанные (и вневписанные) окружности. Одним из вариантов введения их в схему нашего подхода является использование частного случая поризмы Понселе, описанного в [21].

Далее мы остановимся на некоторых достаточно частных вопросах, связанных с изложенным выше материалом. В частности, упомянем один известный, но, скорее всего, малоизвестный факт, связывающий геометрию треугольника с кардиоидой. Пусть треугольник, вписанный в окружность вращается внутри этой окружности, и с помощью неподвижной точки М на этой окружности строятся прямые Симсона для каждого положения вращающегося треугольника. Тогда огибающая этих прямых Симсона, каждая из них привязана к своему треугольнику, представляет собой кардиоиду. Предоставляем доказательство этого факта читателю, а сами ограничиваемся программой, демонстрирующей его.

В том же направлении поиска циклоидальных кривых, связанных с треугольниками, направляет мысли геометра и следующий чертёж, на котором показано геометрическое место точек ортопола неподвижной прямой относительно треугольников, вращающихся внутри описанной окружности.

Ещё одно появление сразу трёх кардиоид связано с теоремой 33: которая утверждает, что множество точек ортополов касательных к описанной окружности относительно вписанного треугольника образует кривую Штейнера. Действительно, проекция А1 вершины А на касательную к описанной окружности при вращении касательной описывает подеру окружности. Эта подера является кардиоидой (см. теорему 11). То же самое можно сказать и вершинах В и С. Таким образом, три проекции А1, В1 и С1 движутся по трём кардиоидам, а три прямых А1М, В1М и С1М, параллельных высотам треугольника АВС, пересекаются в одной точке М, вычерчивающей кривую Штейнера.

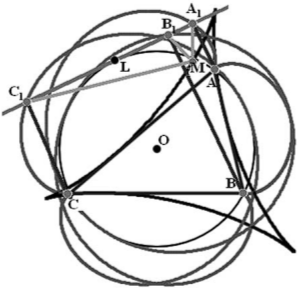
Отметим ещё одно обстоятельство. При доказательстве теоремы 31 можно было заметить, что произвольно выбранный ортоцентр треугольника Н симметричен центру описанной окружности О будущего треугольника относительно центра окружности Эйлера. Если на роль ортоцентра взять точку О, то точка Н станет центром описанной окружности уже другого треугольника. Поскольку кривая Штейнера не обладает центральной симметрией, этот треугольник должен обладать другой формой. В результате на множестве треугольников возникает некое соответствие, разбивающее треугольники на пары. Желательно это соответствие описать.

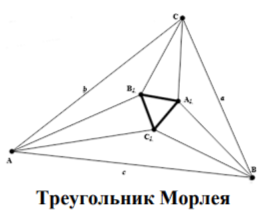
В доказательстве теоремы 32 фактически выясняется, как кривая Штейнера расположена относительно треугольника. Точка S является одной из точек возврата дельтоиды. Это обстоятельство может быть полезно при выяснении некоторых вопросов, например, таких как выяснение взаимного положения кривой Штейнера и различных правильных треугольников, связанных с исходным треугольником. Речь в частности идёт о треугольниках Наполеона и Морлея.

Везде, где речь идёт о кривой Штейнера, возникает вопрос: один (одна) или три? Речь, например, может идти о числе касательных или нормалей к этой кривой, проходящих через определённую точку плоскости.

Для построения в теореме 31 треугольника по точке (ортоцентру), лежащей внутри дельтоиды, важно именно наличие трёх высот. Значит, построить треугольник по точке, лежащей вне дельтоиды невозможно, поскольку через неё проходит только одна прямая Симсона.

При выходе точки Н непосредственно на кривую Штейнера треугольник вырождается, точнее одна из его сторон вырождается в точку. Однако сопоставление треугольников с комплексными числами наводит на мысль, что точки вне кривой Штейнера можно сопоставить с «невозможными» треугольниками, имеющими произвольную длину сторон, в том числе такую, при которой неравенство треугольника не соблюдается.

К этому же кругу вопросов относится и восстановление прямой по её точке ортопола. Поскольку через точку Н внутри кривой Штейнера проходит три прямых Симсона, то можно найти три перпендикулярных им прямых, ортополами которых и является данная точка. Для точки вне кривой такая прямая одна. На границе (в обозначениях теоремы 31) происходит слияние прямых P1Q1 и P2Q2 и превращение в одну прямую PQ. Таким образом, граница, то есть сама кривая Штейнера связана с числом 2.

Наконец, скажем немного о связи геометрии треугольника с вопросами анализа. Поскольку треугольник порождает семейства гладких гипотрохоид, возможность написания дифференциальных уравнений является очевидной.

Кроме того, достаточно ясно, что геометрия треугольника связана с теорией особенностей дифференцируемых отображений или, используя более популярное название этой теории, с теорией катастроф.

Компьютерное построение некоторых чертежей, связанных с геометрией треугольника, навевает ассоциации с трёхмерными изображениями. Приведём пример. Наша программа будет всего на всего строить прямые Симсона некоторого треугольника. Для этого из точки М, движущейся по описанной окружности, мы будем опускать перпендикуляры на две стороны треугольника, получая две точки Р и Т. При этом мы будем проводить не отрезок РТ, а отрезок Р1Т1 в три раза длинней (Р1Р = РТ = ТТ1).

Получить из прямых Симсона реальную поверхность тоже достаточно просто. Рассмотрим горизонтальную плоскость и треугольник АВС на ней. Пусть по описанной окружности движется точка М, порождающая прямые Симсона. Создадим два вертикальных дубликата описанной окружности, повернув её относительно хорд АВ и ВС в вертикальное положение. Пусть по ним синхронно с точкой М движутся точки М1 и М2. Тогда движущаяся пространственная прямая М1М2 проектируется на прямые Симсона и одновременно заметает некоторую поверхность, называемую торсовой с двумя плоскими направляющими (обе являются окружностями) [22].

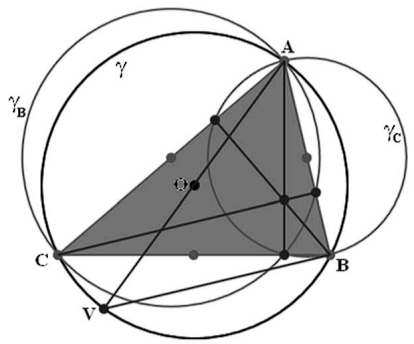
Наконец, интерес представляет и вопрос о взаимном расположении прямых Симсона различных треугольников. При этом основания перпендикуляров при построении прямых Симсона могут оказаться точками ортопола относительно других треугольников. Рекомендуем рассмотреть с этой точки зрения треугольник AVB, который находится с окружностями y и Ye в таком же положении, как треугольник АВС с окружностями y и Y В.

15. ВЫВОДЫ

В статье отмечена неправильная трактовка планиметрии евклидовой плоскости, которая согласно Эрлангенской программе Клейна определяется группой движений, то есть группой преобразований, оставляющих евклидовы расстояния неизменными. В принципе это ошибочное мнение затрагивает вопрос, находящейся на периферии интересов современных математиков, и ни в коей мере не затрагивает значимость идей, высказанных Феликсом Клейном. Тем не менее, ошибка должна быть устранена. Рассмотрение данного вопроса потребовало:

• изложения довольно большого числа хорошо известных фактов, относящихся к различным разделам геометрии;

• построения группы переводящей любой треугольник в любой другой;

• и привело к постановке ряда вопросов, которые не могут быть разрешены и подробно изложены в данной статье.

Итак, в статье приводятся:

1. Теория циклоидальных кривых без использования сколько-нибудь сложных методов дифференциальной геометрии. Их заменили соображения кинематического характера.

2. Некоторые факты геометрии треугольника, необходимые для построения соответствующей группы преобразований, в том числе и важнейшая для всего изложения теорема Штейнера о прямых Симсона.

В статье показано, что:

1. Каждой внутренней точке области, ограниченной кривой Штейнера соответствует некоторый треугольник.

2. Среди этих треугольников можно найти треугольники любой формы.

3. Тем самым, группа преобразований внутренней области, ограниченной кривой Штейнера, является и группой преобразований, действующей на множестве треугольников. Эта группа в отличие от группы движений и групп аффинных и проективных преобразований не является группой точечных преобразований.

4. На роль данной группы после установления гомеоморфизма между внутренней областью, ограниченной кривой Штейнера, и единичным кругом на комплексной плоскости может быть взята группа дробно-линейных преобразований.

5. Доказаны теоремы о связи ортопола с прямыми Симсона. В частности доказано, что точки ортопола касательных к описанной окружности образуют кривую Штейнера.

6. На основе понятия ортопола построено отображение плоскости, порождаемое фиксированным на ней треугольником.

7. Отмечена связь геометрии треугольника с теорией особенностей дифференцируемых отображений.

Перечислим ряд вопросов, которые требуют дополнительного рассмотрения.

1. Вопрос о выборе наиболее удачного гомеоморфизма между внутренней областью, ограниченной кривой Штейнера, и единичным кругом на комплексной плоскости, который естественным образом связал бы совокупности треугольников с такими объектами геометрии Лобачевского как прямые, окружности, орициклы и эквидистанты. В частности интересно было бы рассмотреть прообразы диаметров кривой Штейнера.

2. Факт разбиения всего множества треугольников на совокупности, соответствующие либо объектам геометрии Лобачевского, либо объектам, порождаемым геометрией кривой Штейнера, позволяет изучать геометрические места замечательных точек для каждой из таких совокупностей. Например, можно изучить геометрическое место центров вписанных окружностей для семейства треугольников, соответствующих одному из диаметров кривой Штейнера.

3. Установление соответствия между комплексными числами, по модулю меньшими единицы, и евклидовыми треугольниками делает возможным разработку «исчисления треугольников». В частности, очевидно, что возможно их «перемножение», «нахождение среднего арифметического», «сопряжение» и т. д.

4. Если построить функции, вычисляющие по комплексному числу, соответствующему данному треугольнику, длины его сторон, то возможно рассмотрение, условно говоря, «мнимых треугольников», то есть тех, которым соответствуют комплексные числа, по модулю большие нуля. Видимо, их длины сторон либо, оставаясь действительными числами, не подчиняются соответствующим неравенствам, либо эти длины становятся комплексными числами.

5. Подобные же функции могут быть построены для вычисления параметров замечательных точек, прямых и кривых, связанных с треугольником, и, тем самым, эти понятия могут быть перенесены на множество «мнимых треугольников».

6. Желательно детально изучить связи геометрии треугольника с теорией особенностей дифференцируемых отображений.

7. Нужно установить продуктивность применения предлагаемого подхода к основным результатам геометрии треугольника.

1. В. И. Молодший. Основы учения о числе в XVIII и начале XIX века. М., Учпедгиз, 1963.
2. Е. Н. Берёзкин. Курс теоретической механики. М., Изд. МГУ, 1974.
3. А. А. Савёлов. Плоские кривые: Систематика, свойства, применения. М., Книжный дом «Либроком», 2009.
4. Г. Н. Берман. Циклоида. М., Наука, 1980.
5. В. И. Арнольд. Математические методы классической механики. М., Наука, 1974.
6. В. И. Иванов, В. Ю. Попов. Конформные отображения и их приложения. М., Едиториал УРСС, 2002.
7. М. А. Лаврентьев, Б. В. Шабат. Методы теории функций комплексного переменного. М., Наука,1965.
8. А. И. Маркушевич. Краткий курс теории аналитических функций. М., Гос. изд. физ.-мат. лит., 1961.
9. Викепедия. Задача об иголке.
10. Г. С. М. Кокстер. Введение в геометрию. М., Наука, 1966.
11. Н. Б. Васильев, В. Л. Гутенмахер. Прямые и кривые. М., Наука, 1978.
12. А. Мякишев. Прогулки по окружностям: от Эйлера до Тейлора. Математика: Всё для учителя. № 6, 2011, Издательская группа «Основа».
13. Д. Ефремов. Новая геометрия треугольника. Одесса, Матезис, 1902.
14. Энциклопедия элементарной математики. Книга четвёртая. Геометрия. М., Гос. изд. физ.-мат. лит., 1963.
15. С. И. Зетель. Новая геометрия треугольника. М., Учпедгиз, 1962.
16. В. В. Прасолов. Задачи по планиметрии, ч. 1 – 2. М., Наука, 1996.
17. Е. Д. Куланин, С. Н. Федин. Геометрия треугольника в задачах. М., Книжный дом «Либроком», 2009.
18. Е. Д. Куланин, Н. А. Шихова. Геометрический фейерверк: Творческие задания на уроках математикию М., Илекса, 2016.
19. Е. Д. Куланин. О прямых Симсона, кривой Штейнера и кубике Мак-Кэя. Математическое просвещение, сер. 3, вып. 10, 2006.
20. Е. Д. Куланин. Виктор Тебо и его задачи. Математическое просвещение, сер. 3, вып. 11, 2007.
21. М. Е. Степанов. Образ силового поля как эвристическая модель в математике. Моделирование и анализ данных: Труды факультета информационных технологий МГППУ, вып. 3. М., Русавиа, 2007.
22. С. Н. Кривошапко, В. Н. Иванов, С. М. Халаби. Аналитические поверхности. М., Наука, 2006.