Формулируется стохастическая двухуровневая задача размещения предприятий, в которой фигурируют два игрока: лидер и последователь. Первым свои предприятия размещает лидер, а затем последователь. Доход, получаемый от потребителей, предполагается случайным. На этапе принятия решения игрокам известен только закон распределения случайного дохода. Цель обоих игроков состоит в максимизации гарантированной с заданной вероятностью прибыли. Для случая гауссовского распределения случайных параметров задача сводится к детерминированной двухуровневой задаче. Для решения полученной задачи предлагаются два алгоритма, основанные на адаптации метаэвристических методов: метода имитации отжига и метода поиска с чередующимися окрестностями. На примере задачи размещения электростанций проводится сравнение эффективности двух разработанных алгоритмов.
1. ВВЕДЕНИЕ
Задача конкурентного размещения предприятий описываются ситуацию, когда двое игроков в установленном порядке размещают свои предприятия с целью получения максимальной прибыли. Постановка данной задачи, методы ее исследования и ряд алгоритмов ее решения описаны в работе [Береснев, 2010].
Для описания исследуемой задачи используется аппарат двухуровневой оптимизации [4,5]. Двухуровневые модели описывают взаимодействие двух игроков, поочередно принимающих решения. При этом предполагается, что игроки владеют полной информацией друг о друге. Применение моделей данного класса в близких задачах энергетики обсуждается в [Dempe S, Kalashnikov, 2015].
В силу случайной природы спроса на производимую продукцию на этапе принятия решения игрокам может быть неизвестна реализация спроса в момент реализации продукции. Поэтому возникает необходимость рассмотрения стохастических задач размещения предприятий. Обзор работ в этом области можно найти в [Snyder, 2006]. Если лицу, принимающему решение, необходимо обеспечить гарантированную с некоторой вероятностью прибыль, то целесообразно использовать аппарат задач стохастического программирования с квантильным критерием. Квантильный критерий [Кибзун, 2009] описывает уровень потерь, который не может быть превышен с заданной вероятностью.
Задача конкурентного размещения предприятий с квантильным критерием была сформулирована в работе [Иванов, 2016], где рассматривался случай дискретного распределения случайных параметров. При этом предполагалось, что реализация случайных параметров неизвестна только лидеру, тогда как последователь принимает решение при уже известной реализации спроса. Для данной задачи предложен метод поиска локально-оптимального решения и метод поиска нижней оценки оптимального решения. В [Melnikov, 2016] на основе комбинаторных методов предложен метод поиска улучшенной нижней оценки оптимального решения данной задачи.
В статье рассматривается двухуровневая задача конкурентного размещения предприятий в форме квантили в пессимистической постановке, т.е. лидер, при поиске оптимального решения, учитывает наихудшую для себя стратегию последователя. В отличие от [2,6], в исследуемой задаче ни лидеру, ни последователю не известны реализации случайных параметров. Для поиска оптимального решения лидера предлагается два алгоритма, основанные на метаэвристических методах: методе имитации отжига и поиске с чередующимися окрестностями.
2. ПОСТАНОВКА ЗАДАЧИ
Сформулируем стохастическую задачу конкурентного размещения предприятий. Предполагается наличие двух игроков, по очереди размещающих свои предприятия с целью получения максимальной прибыли. Первый игрок называется лидером, а второй - последователем. Приведем описание параметров и оптимизационных переменных исследуемой математической модели.


где первая сумма выражает затраты на размещение предприятий, а вторая сумма - полученную прибыль от потребителей с учетом возможного перехода потребителей к последователю после открытия новых предприятий. Естественно, лидер стремится обеспечить отрицательное значение функции потерь, что соответствует получению положительной прибыли.
Аналогичным образом записывается функция потерь последователя:

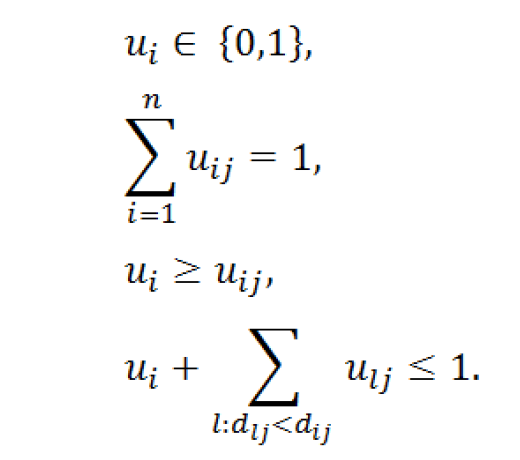
Из второго ограничения следует, что лидер должен для обслуживания каждого потребителя назначить одно и только одно предприятие. Из третьего ограничения следует, что лидер может назначать для обслуживания потребителей только открытые предприятия. Четвёртое ограничение учитывает предпочтения потребителей, запрещая назначать для их обслуживания менее предпочтительные предприятия, чем уже открытые. Максимум в постановке задачи значит, что в случае нескольких оптимальных стратегий последователя лидер учитывает наихудшую для себя, что соответствует так называемой пессимистической постановке задачи двухуровневой оптимизации.
3. ИССЛЕДОВАНИЕ ЗАДАЧИ



4. ОПИСАНИЕ МЕТАЭВРИСТИЧЕСКИХ МЕТОДОВ



5. РЕЗУЛЬТАТЫ ВЫЧИСЛЕНИЙ
На примере задачи конкурентного размещения электространций проведен численный эксперимент, в котором лидер и последователь размещают электростанции в ?i = 7 местах. Лидер
и последователь поочередно размещают свои предприятия, основываясь на полученной прибыли от потребления электроэнергии потребителями, <?! = 100. Лидер и последователь учитывают наилучшие комбинации размещения друг друга, расставляя свои электростанции. Так же и лидеру, и последователю известны предпочтения потребителей по каждому из мест для размещения электростанций.
При решении задачи методом имитации отжига были получены графики изменения квантили функции потерь, представленные на рис.1.
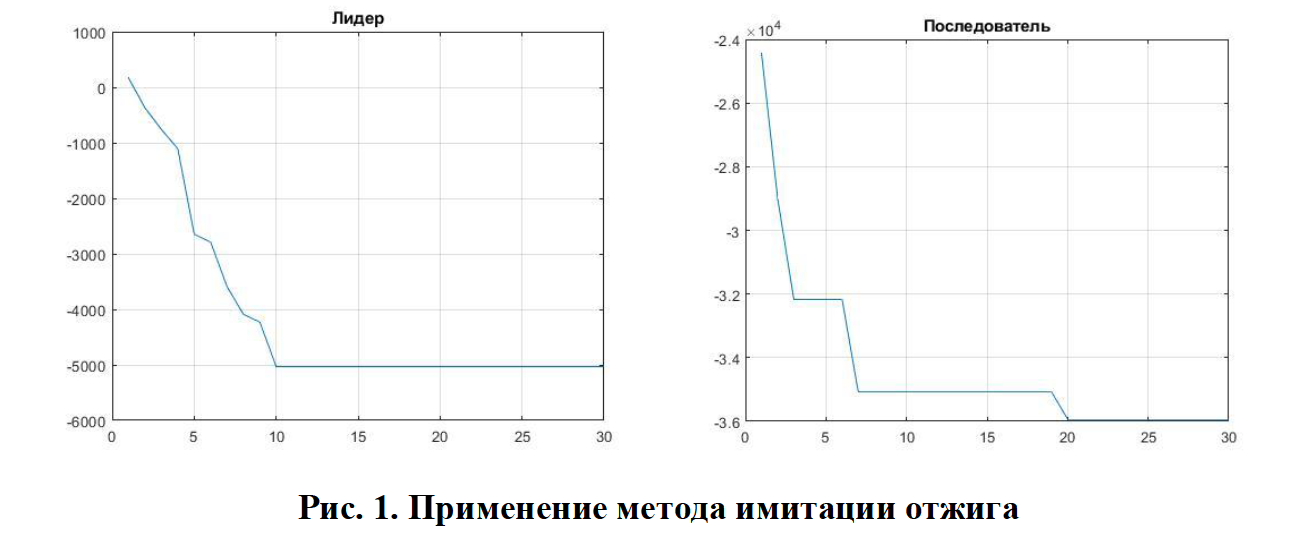
В результате решения задачи найдены стратегия лидера: u = (1 0 1 0 0 0) и стратегия последователя: y = (0 1 0 0 1 0).
При решении задачи методом поиска с чередующимися окрестностями получены графики изменения квантили функции потерь, представленные на рис. 2.
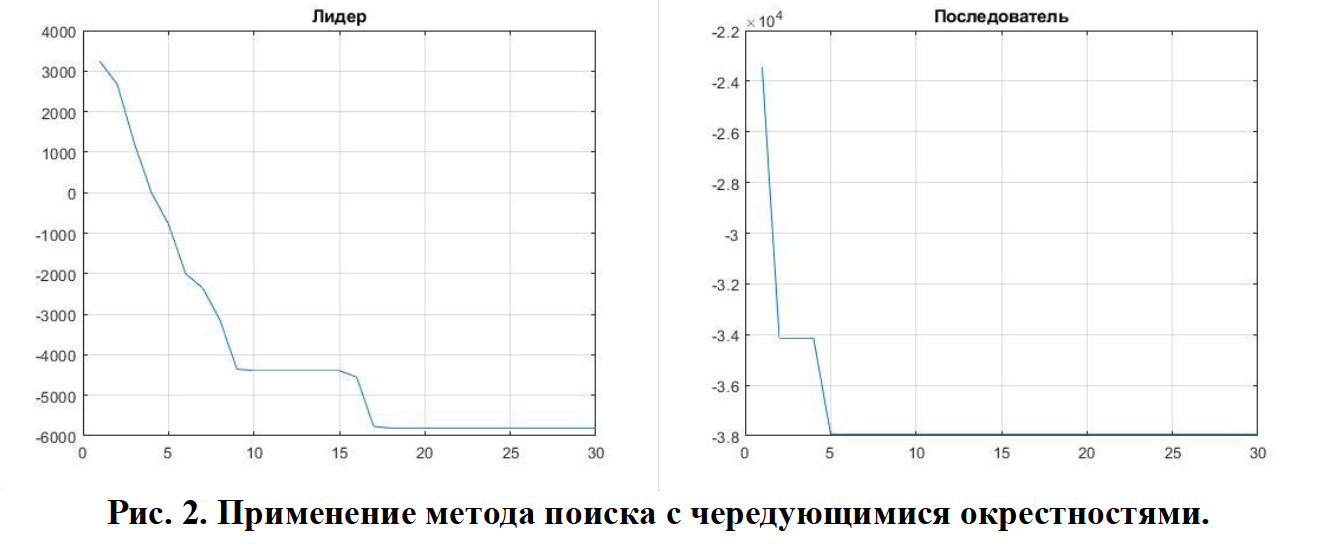
В результате решения найдена стратегия лидера u = (1 0 1 1 0 0) и стратегия последователя y = (0 1 0 0 0 1).
Таким образом, видно, что с помощью поиска с чередующимися окрестностями в данном примере удалось найти решение с меньшим значением минимизируемой функции, чем при применении метода имитации отжига. Это обусловлено тем, что метод поиска с чередующимися окрестностями, в отличие от метода имитации отжига, использует окрестности, в которых могут меняться более двух элементов вектора размещений.
6. ЗАКЛЮЧЕНИЕ
В работе сформулирована новая стохастическая задача размещения предприятий, в которой ни лидеру, ни последователю не известны реализации случайных параметров задачи. Для случая гауссовского распределения случайных параметров задача сведена к детерминированной двухуровневой задаче, для решения которой адаптированы два метаэвристических метода: метод имитации отжига и метод поиска с чередующимися окрестностями. Для рассмотренного численного примера метод поиска с чередующимися окрестностями позволил найти решение с меньшим значением оптимизируемой функции.
ФИНАНСИРОВАНИЕ
Работа выполнена при поддержке гранта РФФИ № 17-07-00203А.