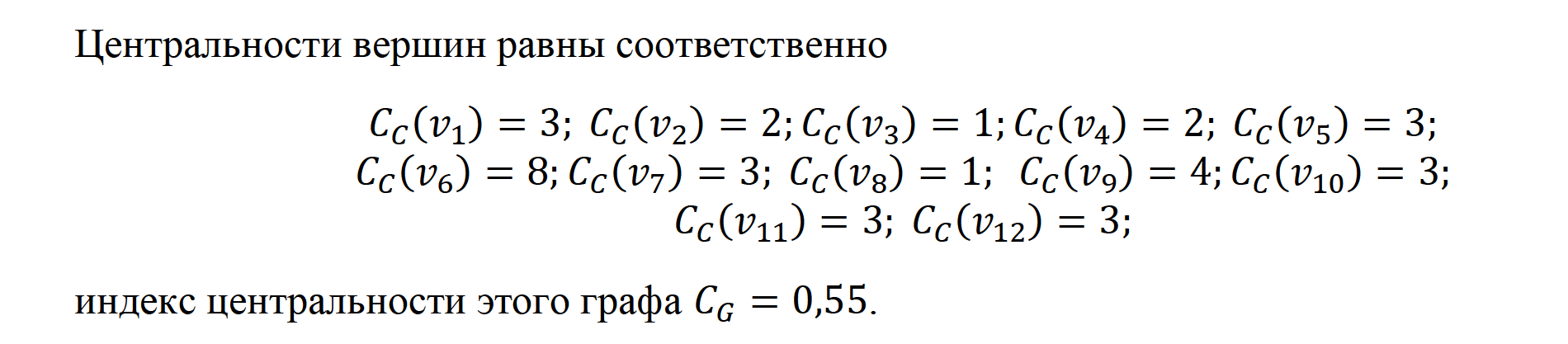Метод оценки влияния вершин при анализе сетевых структур

В статье предложен подход к анализу оценки влияния вершин при анализе сетей. Наряду с понятием центральности вершины рассматривается понятие центральности сети. Предлагается в качестве показателя оценки влияния вершины (актора) на топологию сети рассматривать понятие ключевой вершины, а также характеристику, близкую по своей структуре к индексу Банцафа.

ВВЕДЕНИЕ

В последнее время задача анализа различных сложных сетей, в частности исследование их структуры и определение ключевых элементов, становится актуальной и занимает особое место наряду с другими исследованиями сетей. Топология сетей, отражающих взаимодействие вершин, оказывает влияние на принятие решений, связанных с их анализом. Сетевая топология представляется структурой в виде графа, вершинам (акторам, при исследовании социальных сетей) которого соответствуют узлы сети, а рёбрам — физические или информационные связи между вершинами. Различают различные виды сетевых топологий: полносвязная, неполносвязная (может применяться передача данных не напрямую между компьютерами, а через дополнительные узлы), элементарные: шина, звезда, кольцо.

Важной характеристикой сети является понятие центральности вершины. Различные определения центральности сводится к трем основным концепциям [1,5], рассмотренным ниже. Все они определяют некоторую меру, характеризующую важность актора. Наряду с понятием центральности вершины характеристикой сети выступает также понятие центральности самой сети.

В работе предлагается в качестве показателя оценки влияния вершины (актора) на топологию сети рассматривать понятие ключевой вершины, а также характеристику, близкую по своей структуре индексу к Банцафа, основанному на вычислении доли подграфов, в которых вершина является ключевой.

1. ДОСТАТОЧНАЯ ЦЕНТРАЛИЗОВАННОСТЬ СЕТИ И ОЦЕНКА ВЛИЯНИЯ ВЕШИНЫ (АКТОРА)

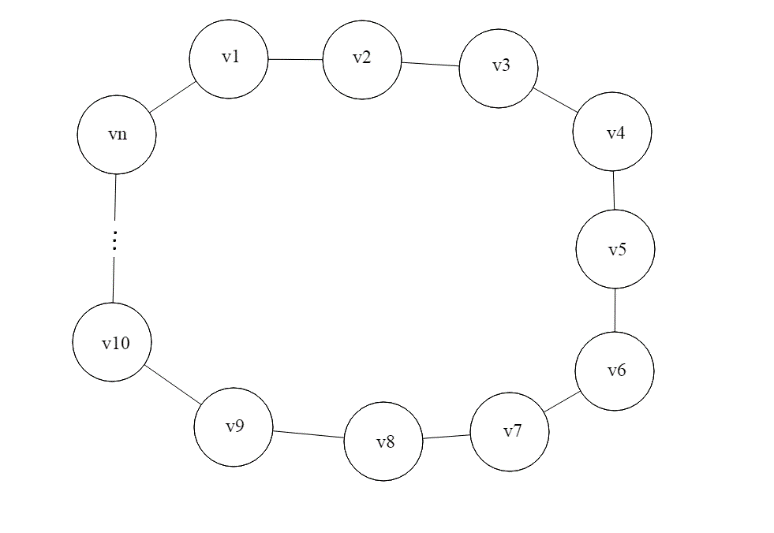
Рис.1 Граф кольцо

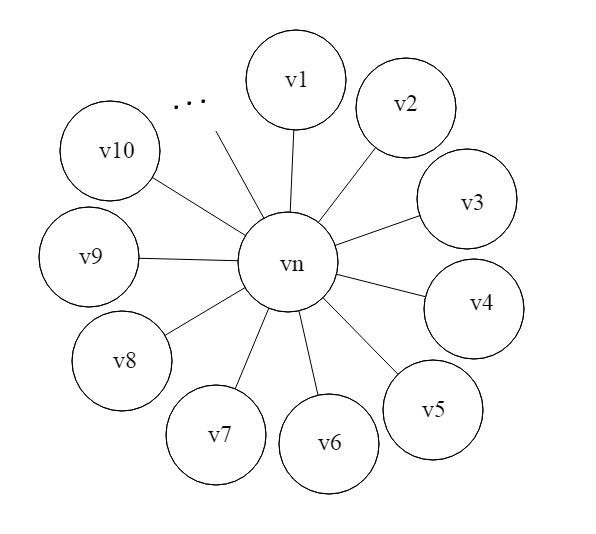
Рис.2 Граф звезда

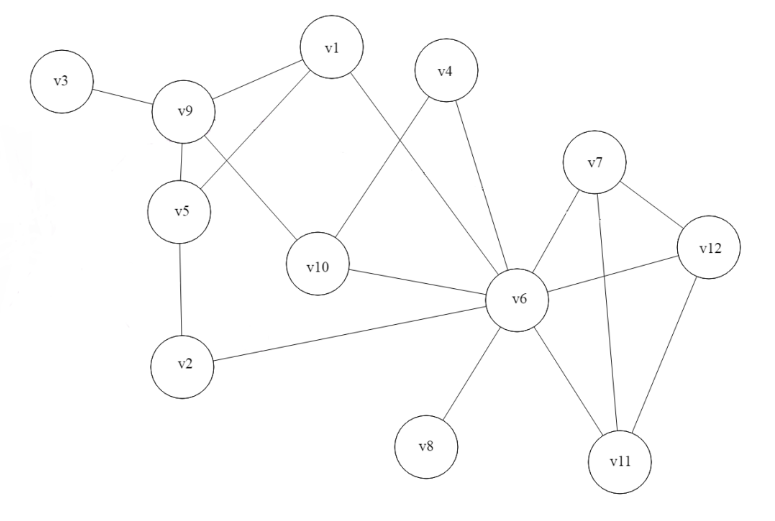
Рис.3 Граф  смешанной топологии сети с 𝒏 = 12  вершинами

1. Freeman L. C. Centrality in social networks. Conceptual clarification // Soc. Networks. 1978/79. V. 1. P. 215-239.
2. Leavitt H. J. Some effects of certain communication patterns on group performance // J. Ab-norm. and Soc. Psychology. 1951. V. 46. P. 38-50.
3. Bavelas A. A mathematical model for group structure // Human Organization. 1948. V. 7. P. 16-30.
4. Алескеров Ф.Т., Хабина Э.Л., Шварц Д.А. Бинарные отношения, графы и коллективные решения. – М.: ФИЗМАТЛИТ, 2017. – 344 с.
5. Щербакова Н.Г. Меры центральности в сетях. – Институт вычислительной математики и математической геофизики СО РАН,630090, Новосибирск, 2015. – 13 с.