Осязаемая предметность с компьютерной поддержкой

В статье рассматриваются перспективы внедрения идеи соединения материальных осязательных объектов, предназначенных для ознакомления учащихся с математическими понятиями, и сопровождающих эти объекты обучающих программ. Тем самым была выдвинута идея осязаемой предметности с компьютерной поддержкой в учебный процесс Компьютерная поддержка осязаемой предметности в любых её формах является средством достижения наилучших условий для самостоятельного изучения учащимися с дефектами зрения некоторых вопросов математики. По этой причине желательно вести разработки программного обеспечения в этом направлении.

Введение

Методическая проработка курса лекций или семинарских занятий является неотъемлемой частью преподавательской работы. Работают в этом направлении и авторы данной статьи [1-3]. Однако в силу специфики учебного заведения преподавателям приходится заниматься достаточно нестандартными методическими вопросами.

Одним из важных направлений работы факультета информационных технологий Московского государственного психолого-педагогического университета является работа с инвалидами, в том числе и по зрению. По этой причине практически каждому преподавателю факультета приходится, так или иначе, задумываться над вопросами тифлопедагогики (см., например, [4]).

Тифлопедагогика сопряжена с постоянным решением различных проблем, возникающих как перед учащимися, так и перед преподавателями. По этой причине решать эти проблемы следует совместно, в постоянном творческом диалоге. Это в равной мере относится и к вопросам частного характера, связанным с изучением конкретных тем, и к вопросам, касающимся выработки общих приёмов преподавания. Данная статья в известном смысле является результатом такого диалога.

Осязаемая предметность с компьютерной поддержкой

В ходе общего обсуждения проблем обучения студентов с дефектами зрения Нгуен Ву Куангом была высказана идея соединения материальных осязательных объектов, предназначенных для ознакомления учащихся с математическими понятиями, и сопровождающих эти объекты обучающих программ. Тем самым была выдвинута идея осязаемой предметности с компьютерной поддержкой. Рассмотрению перспектив внедрения этой идеи в учебный процесс как раз и посвящена данная статья.

Первой конкретной реализацией данной идеи стала тема «Осязаемый треугольник с целочисленными длинами сторон». Основными аспектами данной работы стали

1. Выбор механической модели треугольника, позволяющей легко формировать достаточно многочисленный набор осязаемых треугольников.

2. Выбор основных параметров треугольника, информировать о которых должна сопровождающая компьютерная программа.

3. Разработка программы с продуманным интерфейсом и удобным для обучаемого способом выдачи информации.

В ходе конкретного воплощения проекта в жизнь было решено использовать для создания осязаемых моделей треугольников детали детского металлического конструктора, называемые планками (рис. 1). Они позволяют без каких-нибудь затруднений собирать модели именно тех треугольников, которые имеют целочисленную длину сторон (с точностью до подобия). Для этого соединяют три линейных планки с отверстиями с помощью винтов и гаек. Осязать подобную модель можно, как ощупывая плоскую часть планок с отверстиями, так и проводя пальцем по внутреннему треугольному отверстию в осязаемой модели.

В качестве параметров, которые вычисляются по длине сторон и комментируются поддерживающей компьютерной программой, рассматривались величины углов треугольника, длины таких замечательных отрезков как высоты, биссектрисы и медианы. Кроме того, программа вычисляет площадь треугольника и радиусы описанной, вписанной и вневписанных окружностей.

Все эти величины рассматриваются в школьном курсе планиметрии, но продвинутые варианты поддерживающей программы могли бы информировать учащегося более подробно, давая соответствующие определения.

Необходимо отметить, что предлагаемый способ осязательного знакомства с треугольниками носит особый характер, отличный от традиционных методов изучения евклидовой геометрии. По этой причине необходимо сосредоточиться на построении соответствующих методик, связывающих осязательный метод обучения с классическим методом, базирующемся на основе логических построений. При этом нелишне будет вспомнить об идеях И.М. Сеченова, изложенных в его книге [5], которую И.П. Павлов назвал гениальным взмахом русской научной мысли.

Возможно, многие идеи Сеченова в наше время несколько устарели, но при разработке методик, связанных с осязанием предметов, они, как кажется авторам, очень полезны. В книге Сеченова последовательно развивается мысль о том, что основой деятельности мозга являются рефлексы. В наше время сводить духовный мир человека к одним рефлексам невозможно. Тем не менее, более широкая трактовка следующих идей Сеченова может быть полезна, поскольку она тесно связывает телесные и духовные действия человека воедино. А эта связь особенно ярко проявляется в тифлопедагогике.

Кратко повторим хрестоматийные положения из книги великого русского учёного. Рефлекс - это устойчивая реакция организма на определенное внешнее воздействие. Если деятельность мозга основана на рефлексах, то наш внутренний духовный мир есть отражение мира внешнего (добавим от себя: хотя бы отчасти). В конечном счёте, первопричина любого действия человека исходит из внешнего мира: постороннее воздействие - возбуждение нерва - реакция мозга - движение организма. Это «движение» нужно понимать весьма широко. Оно включает в себя и духовную жизнь человека. При этом мысль трактуется И.М. Сеченовым как рефлекс с задержанным окончанием, а эмоции как рефлексы с усиленным окончанием. При создании методик, основанных на осязании и направленных на развитие мышления, необходимо иметь это в виду.

Материалы для создания осязаемой предметности

Коснёмся вопроса о выборе материалов для создания осязаемой предметности. На первый взгляд речь идёт о чём-то второстепенном, но, на наш взгляд, до тех пор, пока технологии создания осязаемой предметности не сформированы в должной мере, интерес могут представлять даже варианты, которые кажутся кустарными. В качестве подтверждения напомним о японской фирме, которая процветала, используя и развивая идеи читателей отечественного журнала «Наука и жизнь», придумывающих различные бытовые приспособления.

Кроме довольно технологичного варианта создания осязаемых треугольников из деталей конструктора нами рассматривался «кустарный» вариант использования трубочек для сока и коктейлей. Из них без труда можно вырезать детали нужной длины. Соединить их можно различными способами:

1. Продев нитку (рис. 2).

2. Шариками пластилина.

3. Проволочками (рис. 3).

Вернёмся к технологиям, которые основаны на использовании деталей конструктора. На этой же основе авторами рассматривались варианты осязательного метода, более близкие к курсу аналитической геометрии, чем описанный выше. Речь идёт об использовании осязаемых моделей, для которых целые значения имеют не длины, а координаты вершин плоских и объёмных фигур. В простейшем случае речь идёт о треугольниках с целочисленными координатами вершин.

Их можно моделировать с помощью таких деталей конструктора, как основания (рис. 4) и пластины (рис. 5), а также хорошо осязаемых шнуров.

Компьютерная поддержка данных осязаемых моделей требует вычисления длин сторон треугольника по координатам вершин. При этом используется теорема Пифагора, а поочерёдное ощупывание и подсчёт отверстий на пластине по её ширине и высоте обосновывает правильность вычислений и делает их наглядными, насколько это возможно.

Легко понять, что данный вид плоских моделей позволяет изучать многоугольники различного вида, в том числе такие важные четырёхугольники как параллелограммы, трапеции, ромбы и т.д. Для каждого вида многоугольников должна быть написана специальная поддерживающая программа.

Кроме того, точно такие же модели можно использовать при изучении векторной алгебры на декартовой плоскости. Речь идёт о сложении и вычитании векторов, а также об их разложении по заданным направлениям.

В том же духе (детали конструктора и шнуры) можно развивать технологию создания объёмной осязаемой предметности. При этом следует использовать многоярусные модели. Начнём с описания тетраэдров с целочисленными координатами вершин. С помощью двух оснований создаётся двухъярусная конструкция, на которую натягиваются шнуры-рёбра (рис 6, 7).

Возможно создание более сложных объёмных двухъярусных моделей. Речь идёт о моделях пирамид (при большом числе рёбер, передающих также форму конусов), призм (при большом числе рёбер, передающих также форму цилиндров) и линейчатых поверхностей второго порядка. В технологические тонкости мы не вдаёмся, поскольку общая идея ясна, а конкретная проработка проекта требует учёта многочисленных деталей.

Затронем только один вопрос. Он связан с тем, что каждому виду объёмных осязаемых моделей должна соответствовать своя форма пластин, образующих ярусы, а также взаимное расположение этих пластин. Так для создания моделей призм можно использовать две круглых пластины, соединённых в двухъярусную конструкцию вертикальным стержнем. Ещё одним полезным примером являются антипризмы.

На рисунке 8 без прорисовки технических деталей изображена пятиугольная антипризма. При этом понятно, что каждая из двух пластин должна быть пятиугольником и что пятиугольники по отношению друг к другу должны быть повернуты особым образом.

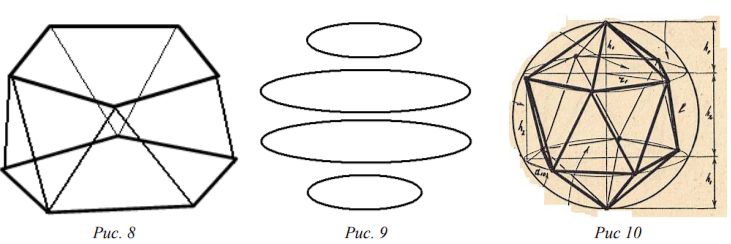
На одном стержне могут держаться и многоярусные конструкции, предназначенные для создания осязаемых моделей более сложных тел. На использовании многоярусных моделей можно построить изучение многогранников, в том числе платоновых тел. На рисунке 9 показана схема четырёхуровневой конструкции, которую можно использовать для моделирования икосаэдра и додекаэдра. А рисунок 10 помогает понять, что осязаемая модель икосаэдра расслаивается на три двухуровневые модели - две пятиугольных пирамиды и антипризма.

Как предварительный итог мы можем констатировать, что представляется перспективным направлением работы создание специально ориентированных на тифлопедагогику осязательных конструкторов, в частности основанных на использовании деталей обычных металлических конструкторах с добавлением шнуровых технологий. Одно из достоинств таких конструкторов должно состоять в том, что обучаемый сможет самостоятельно создавать модели плоских фигур и объёмных тел, а не только осязать готовые.

Видимо, здесь можно использовать и дополнительные возможности. В частности в интернете высказано мнение, что изгибание деталей металлических конструкторов открывает поистине безграничные возможности для конструирования. Однако здесь нужна детальная проработка вопроса. Ещё одним перспективным направлением представляется использование некоторых головоломок.

У тех читателей статьи, кто концентрирует своё внимание не на координатах вершин многогранников, а только на их форме, может возникнуть вопрос, нужно ли при наличии 3d-принтеров разрабатывать специализированные конструкторы? Не лучше ли с помощью 3d-технологий создавать наборы осязаемых моделей математических объектов и оснащать их компьютерной поддержкой? Ответ достаточно очевиден: следует использовать все доступные варианты моделирования осязаемой предметности.

Отметим, что история создания соответствующих стационарных осязаемых моделей достаточно продолжительна. На картинах Леонардо многогранники изображаются как объекты, сконструированные из реек. На картине фламандского художника Николы Ней- шталя «Урок геометрии» показано использование такой модели в учебном процессе. В книге [6] описывается технология изготовления многогранников из бумаги. Не редкость геометрические объекты из резины, пластилина и гипса. Последние часто применяются при классических методиках обучения рисованию.

В статье [7] рассказано о производстве гипсовых математических моделей на рубеже XIX - XX веков. Современные 3d-принтеры позволили бы поставить производство подобных моделей математических объектов, которые в равной степени полезно и осматривать, и осязать, на поток. Тем более, что есть очень интересные и перспективные идеи, связанные с наглядной геометрией и наглядной топологией (см., например, [8-11]). Было бы очень полезно превратить рисунки в осязаемые модели, снабдив их компьютерной поддержкой. Тем самым, можно выделить как важное направление разработки осязаемых моделей создание наборов фигур и тел с компьютерной поддержкой.

Изучение кривых механического происхождения

Ещё одна идея, высказанная Нгуен Ву Куангом, связана с трудностями, которые испытывают студенты с дефектами зрения при изучении различных кривых и, прежде всего, кривых механического происхождения. Была начата работа и в этом направлении. В частности была предложена конструкция механизма, который позволяет с помощью осязания изучить возникновение циклоид различного вида (циклоид как таковых, укороченных и удлинённых циклоид). 

Данный механизм состоит из простой механической части, которая показана на рисунке 11. По рейке катится шестерня, на которой закреплена радиальная планка с тремя отверстиями. В каждое из отверстий можно вставить стержень, который будет «прочерчивать» одну из циклоид[12].

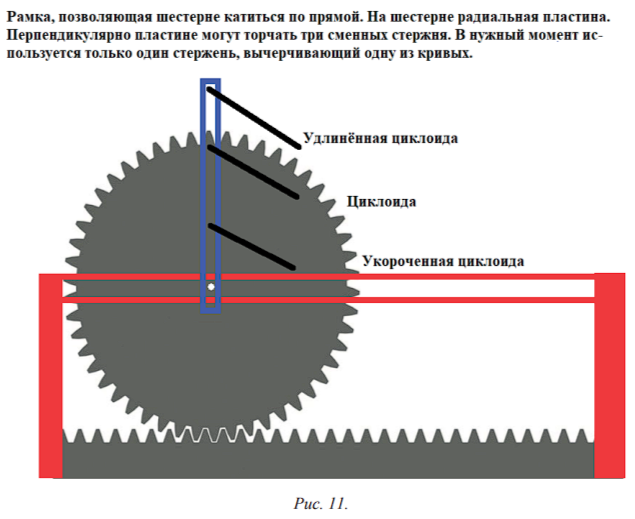
Вторая часть механизма представляет собой пластину, в которой прорезана одна из циклоид. Таких пластин три. Форма прорезей показана на рисунке 12 (на рисунке они совмещены). В зависимости от положения стержня, вычерчивающего кривую, к механизму прикрепляется одна из этих пластин. Вычерчивающий стержень при качении шестерни скользит в прорези. Как результат форма кривой не только осязается, но и увязывается с механическим процессом.

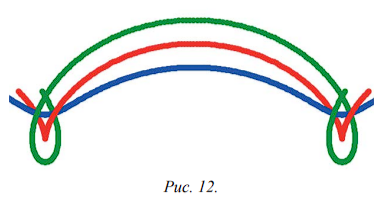
Аналогичным образом можно разработать механизмы для изучения циклоидальных кривых и трохоид [12]. В настоящее время делается попытка по созданию действующих моделей соответствующих механизмов.

Возможно также создание механизмов, демонстрирующих не только механическое порождение кривой, но и некоторые дополнительные свойства этой линии. Вкратце опишем механизм, соединяющий процедуру построения эллипса с одновременным построением касательной к нему. Эллипс, как обычно, строится с помощью шнурового кольца (рис. 13), накинутого на два стержня-фокуса С1 и С2. Однако этот шнур, кроме всего прочего, продет через две трубочки механического приспособления, направляющего специально предназначенный для этого стержень BD по касательной к эллипсу (рис. 14).

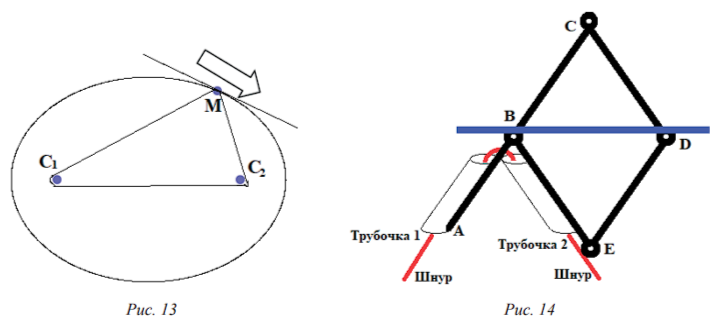
Сделаем несколько пояснений по поводу устройства шарнирного механизма ABCDE. Прежде всего, через трубочки продет шнур. Стержень АВС является единой жёсткой деталью, прикреплённой к первой трубочке. Стержень ВЕ прикреплён ко второй трубочке. Трубочки с прикреплёнными к ним стержнями свободно могут менять взаимное положение с помощью шарнира В. Это позволяет углу АВЕ между стержнями соответствовать углу, образуемому шнуром в точке изгиба (точка М). Шарнирный ромб BCDE обеспечивает перпендикулярность стержня BD биссектрисе угла АВЕ, а это и означает, что стержень BD является касательной к эллипсу (см., например, [1]).

В связи со всем сказанным ранее желательно рассмотреть достижения механики с позиций тифлопедагогики. Например, среди работ И.И. Артоболевского, создавшего отечественную научную школу теории механизмов и машин, есть статьи о механизмах, решающих математические задачи, в том числе и о механизмах, вычерчивающих эллипсы [13]. Более того, в популярных математических книгах, например, [8] и [14], рассматриваются вопросы, связанные с шарнирными механизмами. Наконец, есть поучительные и при этом очень несложные механизмы, которые легко создать с помощью простых технологий и материалов. Например, при изучении кривых постоянной ширины можно использовать, легко моделируемый треугольник Рело.

В заключение очень кратко коснёмся вопроса об особых формах тифлопедагогических технологий, которые эмулирует либо процесс осязания, либо осязаемые объекты. Речь и об использовании специальных компьютерных технологий и о виртуальных объектах. Более подробно об этом говорится в статье [4]. Суть метода «ощупывания компьютерных изображений» в том, что перемещение указателя по обычному экрану или прикосновение пальца к сенсорному экрану вызывает отклик, выражающийся в изменении силы звука по принципу «тепло - холодно». Для достаточно простых изображений этот метод позволяет воспринять форму виртуального объекта, например, графика функции.

Идея тренажёра «Темная комната»

Скажем ещё и об использовании осязаемых объектов нестандартной конструкции и нестандартных размеров. Теоретическое рассмотрение этих вопросов только начато. По этой причине излагаем лишь набросок соответствующей идеи. Исходной точкой при возникновении обсуждаемой идеи был важный и постоянно вызывающий первоочередной интерес вопрос о способах ориентации слабовидящих людей в пространстве города.

Возникла идея создания своеобразных тренажёров, каждый из которых условно может быть назван «тёмной комнатой». Что касается внутреннего наполнения «тёмных комнат», то они могут быть пустыми, наполненными условной мебелью, наконец, многоэтажными. Форма «тёмных комнат» может быть произвольной за счёт использования верёвочных границ и ширм. Речь может даже идти о неких аналогах географических карт.

Теперь о предполагаемых целях использования «тёмных комнат».

1. Психологические исследования возможностей ориентирования за счёт одного осязания, включая оценку возможностей испытуемых по оценке расстояний, форм и способности передать результаты своего пребывания в «тёмной комнате» преемникам. Пример задания для квадратной или круглой комнаты: определить форму, размеры и переместиться в центр комнаты.

2. Привлечение зрячих к экспериментам с целью сравнения их возможностей с возможностями незрячих. Кроме того, такие эксперименты позволят зрячим лучше понять проблемы незрячих.

3. Разработка и проверка эффективности различных компьютерных технологий ориентации в ограниченных пространствах.

4. Выработка методик эффективного описания «тёмных комнат» для передачи информации впервые попадающим в тренажёр.

5. Разработка заданий и методик обучения эффективному ориентированию в «тёмных комнатах»

ЗАКЛЮЧЕНИЕ

В заключении перечислим основные направления деятельности в области создания осязаемой предметности с компьютерной поддержкой.

1. Компьютерная поддержка осязаемой предметности в любых её формах является средством достижения наилучших условий для самостоятельного изучения учащимися с дефектами зрения некоторых вопросов математики. По этой причине желательно вести разработки программного обеспечения в этом направлении.

2. Следует пересмотреть все используемые ранее достижения педагогической науки с точки зрения, исходящей из потребностей тифлопедагогики. Речь идёт о ранее созданных наглядных пособиях, в частности о конструкторах, головоломках, стационарных моделях геометрических объектов.

3. Следует провести пересмотр идей наглядной геометрии и наглядной топологии с позиций тифлопедагогики с целью создания максимально широкого класса осязаемых моделей.

4. Необходим пересмотр достижений механики с тех же позиций.

5. Следует работать над созданием наборов осязаемых моделей геометрических объектов с помощью 3D-npuHTepoB.

6. Следует разрабатывать программы для «ощупывания» виртуальных объектов.

7. Нужно вести разработку тренажёров по типу «тёмной комнаты».

1. Куланин Е.Д., Степанов М.Е. Пропедевтика решения экстремальных задач в школьном курсе математики. Рукопись.
2. Куланин Е.Д., Степанов М.Е. Роль образного мышления в научном мышлении. Рукопись.
3. Степанов М.Е. Некоторые вопросы методики преподавания высшей математики // Моделирование и анализ данных. 2017. № 1. С. 54–94.
4. Степанов М.Е. Из опыта работы в области тифлопедагогики // Моделирование и анализ данных. 2017. № 1. С. 42–53.
5. Рефлексы головного мозга / И.М. Сеченов. – Москва: АСТ, 2015. – 352 с.
6. Веннинджер М. Модели многогранников. – Москва: Мир, 1974. – 236 с.
7. Кутеева Г.А., Синильщикова Г.А., Трофименко Б.В. Математические модели каталога Мартина Шиллинга. Математика в высшем образовании. № 15, 2017.
8. Гильберт Д., Кон-Фоссен С., Наглядная геометрия. – Москва: Наука, 1981. – 344 с.
9. Болтянский В.Г., Ефремович В.А., Наглядная топология. – Москва: Наука, 1982. – 160 с.
10. Франсис Дж. Книга с картинками по топологии. – Москва: Мир, 1991. – 350 с.
11. Фоменко А.Т. Наглядная геометрия и топология: Математические образы в реальном мире. – Москва: Изд. МГУ, 1998. – 416 с.
12. Савёлов А.А. Плоские кривые: Систематика, свойства, применения. М., ЛЕНАНД, 2009.
13. Боголюбов А.Н. Иван Иванович Артоболевский: 1905–1977. Создатель советской научной школы теории механизмов и машин. – Москва: ЛЕНАНД, 2017. – 296 с.
14. Радемахер Г., Теплиц О. Числа и фигуры. – Москва: Физматгиз, 1962. – 263 с.

PlumX

Метрики публикации