Моделирование динамических систем с интервальными параметрами. Обзор методов и программных средств

В работе выполнен обзор существующих библиотек и реализованных в них методов моделирования динамических систем с интервальными параметрами. Рассмотрены доступные библиотеки программ AWA, VNODE-LP, COSY Infinity, RiOT, FlowStar, а также авторский алгоритм адаптивной интерполяции. Рассмотренные библиотеки позволяют находить гарантированные оценки решений, однако с течением времени эти оценки становятся существенно завышенными. За счет использования принципиально другого подхода к построению решений, алгоритм адаптивной интерполяции не подвержен накоплению ошибок, определяет границы решений с контролируемой точностью и работает значительно быстрее аналогов.

Введение

При решении прикладных задач механики, химической кинетики, газовой динамики и других или при исследовании определенных свойств динамических систем часто возникают ситуации, когда какие-либо параметры точно не известны, но есть информация о диапазонах, в которых находятся их значения. Для таких задач является актуальным получение интервальных оценок решений по известным интервальным значениям их параметров. Традиционно подобные задачи формулируются в виде задачи Коши для системы обыкновенных дифференциальных уравнений (ОДУ) с интервальными начальными условиями или параметрами.

Отметим, что аппарат исследования динамических систем достаточно широко развит [1-5] и обобщение его на динамические системы с интервальными параметрами представляет практический интерес.

Выделим несколько групп существующих методов. К первой группе отнесем методы типа Монте-Карло, представленные в работах Соболя И. М. [6], Ермакова С.М., Михай­лов Г.А. [7], Крамера Г. [8], Золотарева В.М. [9] и др. Их суть заключается в проведении многократных расчетов со случайными значениями соответствующих интервальных параметров. Этим методам присущ ряд положительных свойств, таких как простота, высокая степень распараллеливания и отсутствие потребности в аналитической записи правой части ОДУ, но при этом они обладают низкой ( y/N, где N - количество симуляций) скоростью сходимости и требовательны к вычислительным ресурсам.

В качестве альтернативы выступают методы, в основе которых лежат интервальные вычисления. Еще Архимед в свое время использовал интервальные оценки для определения числа пи, но активное развитие интервальные методы получили, начиная с ХХ века в работах Янги Р. [10], Двайера П. [11], Вармуса М. [12], Сунаги Т. [13], Мура Р. [14], Лонера Р. [15], Хансена Э. [16], Алефельда Г. [17], Кравчика Р. [18], Никельи К. [19], Ноймайера А. [20] и др. Среди отечественных родоначальников интервальной математики - Брадис В.М. [21], Канторович Л. В. [22], Шокин Ю.И. [23, 24], Добронец Б.С. [25, 26], Шарый С.П. [27], Рогалев А. Н. [28-30] и др. Из-за своей природы интервальные методы подвержены так называемому эффекту обертывания (эффекту Мура), проявляющемуся в безграничном росте ширины получаемых интервальных оценок решений. Этот эффект возникает вследствие замены точной формы множества решений на более простую форму и для итеративных методов зачастую приводит к экспоненциальному расхождению границ интервалов. Многие из существующих и разрабатываемых методов направлены на борьбу с этим эффектом [31].

Во вторую группу входят методы, основанные на рядах Тейлора. Они в первую очередь ориентированы на получение гарантированных оценок решений, однако эффект обертывания уменьшают не в полной мере. Их идея заключается в аналитическом разложении решения системы ОДУ в ряд Тейлора с последующей оценкой остаточного члена. Для снижения эффекта Мура выполняется запоминание линейных преобразований, которые производились над множеством решений в процессе вычислений. К этим методам относятся метод Мура [14], метод параллелепипедов [32], QR-метод Лонера [15] и др. Они просты и нетребовательны в плане вычислительных ресурсов, но эффективны в задачах, где интервалы не слишком велики или где нелинейность системы ОДУ проявляется слабо. Существует несколько библиотек, реализующих эти методы: AWA [33], VNODE [34], ADIODES [35], VSNODE [36], VNODE-LP [37].

Отдельно стоят методы модели Тейлора, разработанные в Мичиганском университете Берзом М., Макино К. [38-43], Нехером М., Джексоном К.Р., Недялковым Н.С. [44], На- тарым П.С., Сондуром С. [45] и др. В их основе лежит принципиально иной подход. Как и в других методах, основанных на рядах Тейлора, решение здесь раскладывается в ряд Тейлора и выполняется оценка остаточного члена, но при этом все вычисления происходят не в числах и не в интервалах, а в так называемых моделях Тейлора. Модель Тейлора представляет собой полином некоторой степени с интервальным остатком. Она сочетает интервальную арифметику с символьными вычислениями. Эффект обертывания уменьшается за счет установки функциональных зависимостей между начальными условиями и решением в каждый момент времени. Все вычисления с коэффициентами полиномиальной части модели Тейлора выполняются на множестве вещественных чисел, а интервальные границы вычисляются только для остатка ряда. При данном подходе все арифметические операции и стандартные функции должны работать с целыми полиномами в качестве операндов. Такой подход довольно эффективно снижает эффект обертывания, но при этом работа с полиномами выполняется намного медленнее работы с интервалами [46]. Среди библиотек, реализующих данные методы, можно выделить несколько: COSY Infinity [47], RiOT [48], FlowStar [49, 50], verifyode [51] и др. Область сходимости рядов практически всегда ограничена, поэтому в общем случае для решения задач, содержащих «большие» интервалы, в работах Макина К., Берза М. [52], Клеттинга М., Рауха А., Аше- манна Х., Хофера Е.П. [53] и других описываются идеи расщепления исходной области неопределенности на подобласти, которые обрабатываются по отдельности.

К третьей группе отнесем методы, основанные на символьных вычислениях. В частности, это методы модели Тейлора, а также метод, аппроксимирующий оператор сдвига вдоль траектории (Рогалев А.Н. [28-30]). Как и методы модели Тейлора, метод сдвига вдоль траектории в каждый момент времени получает решение в виде символьного выражения относительно интервальных параметров. Эти методы не подвержены или слабо подвержены эффекту обертывания, справляются с широким классом задач, но при этом для них характерна высокая вычислительная сложность и трудности при распараллеливании.

В работах Добронца Б.С. [54, 55], Некрасова С.А. [56] и других приводятся методы, способные находить оптимальные двусторонние оценки решений для систем ОДУ, обладающих определенными свойствами. В основном они построены на теоремах сравнения и, как следствие, применимы только для определенных классов систем ОДУ.

Также стоит упомянуть методы, которые приближают множество решений эллипсоидами, параллелепипедами или многогранниками [57, 58]. Они не лишены свойства завышения оценок, и для них желательным является выпуклость множества.

В общем случае для подавления эффекта обертывания необходимо устанавливать зависимость между интервальными параметрами и решением в каждый момент времени. Зачастую сложность соответствующих методов является экспоненциальной относительно количества интервальных начальных условий или параметров, поэтому очень важно, чтобы они хорошо распараллеливались. В последние годы активно идет развитие программно-аппаратной технологии CUDA, которая позволяет использовать графические процессоры (GPU) компании NVIDIA для общих вычислений. Ключевое отличие GPU от центральных процессоров (CPU) заключается в наличии тысяч ядер, способных одновременно производить расчеты. При использовании даже не очень дорогих видеокарт можно получить прирост производительности в десятки, а то и в сотни раз по сравнению с вычислениями на центральном процессоре. Отметим, что при всей своей привлекательности разработка, ориентированная на GPU, обладает рядом особенностей. Например, вместо наличия только оперативной памяти здесь имеется шесть различных ее видов и возможность напрямую взаимодействовать с кеш-памятью.

Исторически интервальные методы возникли в связи с потребностью в гарантированных вычислениях, которые учитывали бы погрешность самих вычислительных схем, а также ошибки округления при расчетах на ЭВМ. В настоящее время интерес представляют задачи, в которых интервальность возникает непосредственно в самой постановке, а свойством гарантированности можно пренебречь, если есть возможность контролировать точность получаемых границ решений. В связи с этим, авторами данной работы был разработан алгоритм адаптивной интерполяции [59-62], который позволяет за приемлемое время находить интервальную оценку решений с контролируемой точностью, не подвержен эффекту обертывания, имеет высокую степень распараллеливания, справляется с «большими» интервалами и при этом не требует аналитической записи правой части ОДУ и вычисления старших производных.

Идея алгоритма заключается в построении динамической структурированной сетки на основе kd-дерева над множеством, образованным интервальными параметрами задачи. Каждая вершина дерева представляет собой интерполяционную сетку, соответствующую заданной степени интерполяционного многочлена. С каждым узлом сетки сопоставляется решение, найденное при параметрах, определяемых положением узла в пространстве. В процессе выполнения алгоритма на каждом шаге интегрирования исходной системы ОДУ строится кусочно-полиномиальная функция, которая интерполирует зависимость решения задачи от точечных значений интервальных параметров. При наличии такой функции, нахождение интервальной оценки сводится к задаче оптимизации, для решения которой существуют как классические методы [63], так и интервальные [64-66].

Каждая итерация алгоритма состоит из двух этапов. На первом этапе все решения, связанные с узлами интерполяционных сеток, переносятся на следующий временной слой с помощью какого-либо численного метода интегрирования. На втором этапе происходит перестроение kd-дерева по принципу минимизации ошибки интерполяции в вершинах.

Возможность определять наличие в динамической системе бифуркаций и хаоса является важным аспектом при исследовании динамических систем [1, 67, 68]. В связи с этим отметим, что по качественному изменению адаптивной сетки, получающейся в процессе работы алгоритма, можно судить о режимах, которые возникают в динамической системе.

Алгоритм адаптивной интерполяции на основе kd-дерева

Интервальная постановка задачи Коши:

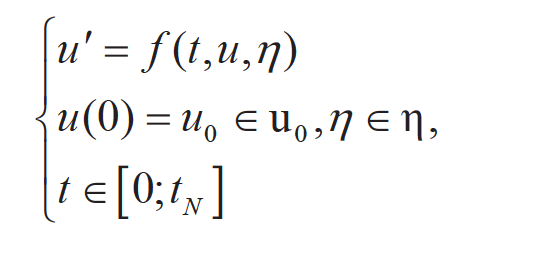
В результате на момент будет получено kd-дерево и соответствующая ему кусочно-полиномиальная функция, интерполирующая решение с заданной точностью. Строить kd-дерево заново для каждого шага нет необходимости, вместо этого используется дерево, полученное на предыдущем шаге, и в зависимости от оценки погрешности интерполяции в его вершинах оно перестраивается (рис. 1). Процесс дробления вершин всегда происходит на предыдущем шаге (пунктирные линии), потому что при создании новых вершин выполняется интерполяция связанных с их узлами значений, и это необходимо выполнять в момент, когда погрешность еще допустима. Если для вершины и всех ее потомков ошибка интерполяции становится приемлемой, то потомки удаляются и сама вершина становится листом.

На практике оценка погрешности интерполяции выполняется только для некоторых точек из соответствующей области (рис. 2). Выделим два подхода к их выбору.

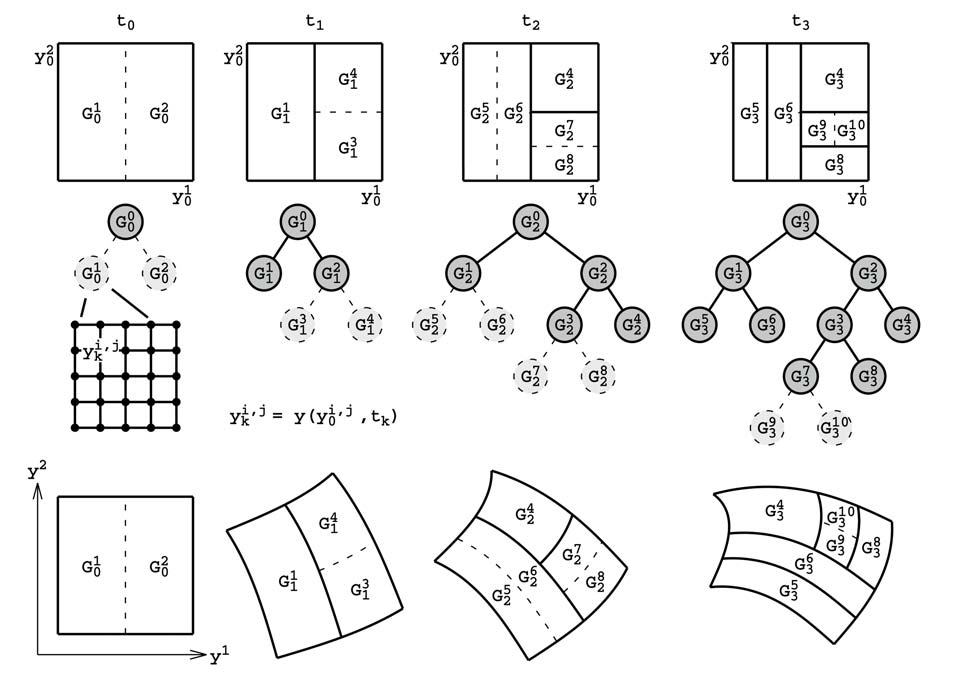
Рис. 1. Иллюстрация работы алгоритма.

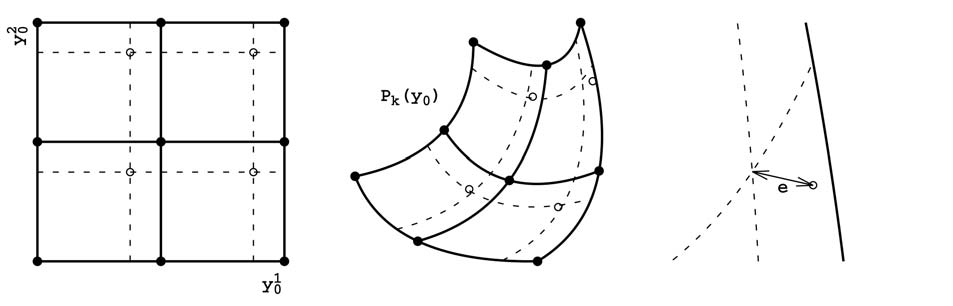
Рис. 2. Оценка погрешности интерполяции. Закрашенные точки - узлы интерполяционной сетки. Выколотые точки - точки, в которых оценивается погрешность интерполяции.

Первый подход заключается в добавлении при создании в каждую вершину случайным образом тестового множества точек. Для оценки погрешности связанные с ними значения сравниваются со значениями, полученными интерполяцией. Использование такого подхода, с одной стороны, позволяет адекватно оценивать погрешность, но, с другой стороны, требует дополнительных вычислительных затрат и дополнительной памяти для хранения вспомогательных точек. Второй подход заключается в удалении из сетки некоторого количества узлов с последующей интерполяцией связанных с ними значений по оставшимся узлам. Данный подход является менее трудозатратным, так как не требует дополнительных узлов, но при этом полученная оценка является завышенной, так как понижается степень интерполяционного полинома.

Методы рядов Тейлора

Рассмотрим интервальную задачу Коши:

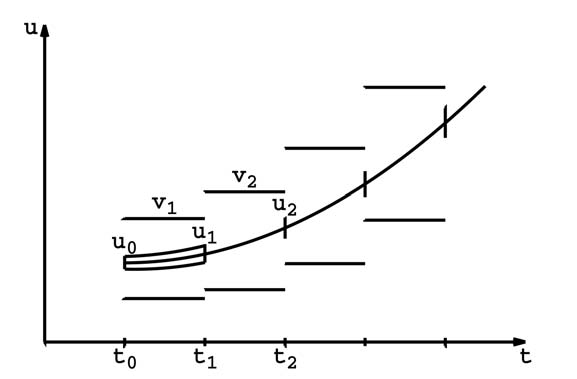
Рис. 3. Априорная оценка решения

Прямой метод Мура никак не компенсирует эффект обертывания. QR-метод Ло- нера отличается от метода параллелепипедов тем, что на каждом шаге область решения заключается в прямоугольный параллелепипед для более эффективного учета локальной ошибки z_j .

Описанные выше методы значительно снижают эффект обертывания, особенно в однородных линейных системах ОДУ с постоянными коэффициентами. Однако при интегрировании нелинейных систем ОДУ эффект обертывания все равно проявляется, хотя и в меньшей мере, и начиная с определенного момента получаемые оценки решения становятся чрезмерно большими и неприемлемыми.

Матрица Якоби характеризует деформацию элементарных объемов пространства. В случае линейной системы ОДУ матрица Якоби постоянна и каждый элементарный объем области деформируется линейно и одинаково, как и в целом вся область. Поэтому область в процессе решения остается параллелепипедом. В случае нелинейной системы ОДУ матрица Якоби в каждой точке области разная. За счет использования интервальной арифметики получается уже интервальная матрица Якоби, содержащая в себе все возможные матрицы во всех точках области. При использовании такой матрицы для деформации заведомо закладывается то, что любой элементарный объем области может быть деформирован любой вещественной матрицей Якоби. Это в конечном счете и ведет к паразитному эффекту.

В работе [31] были предложены несколько модификаций данных методов для снижения эффекта обертывания. Их идея заключается в том, чтобы вычислять матрицу Якоби не для всей области, а только для некоторой заведомо меньшей части или вообще только в одной точке. Использование такого подхода лишает свойства гарантированности, но, как показали численные эксперименты, большая часть решения все равно содержится в получаемой оценке.

Библиотека AWA

Библиотека AWA [33] разработана на Pascal-XSC в 1994 году Лонером Р. для решения ОДУ с гарантированной оценкой погрешности. Данная библиотека представляет собой реализацию QR-метода Лонера в качестве второго этапа и метода постоянного приближения для проверки существования и единственности решения в качестве первого этапа [46].

Библиотека VNODE-LP

Библиотека VNODE-LP [37], это решатель интервальных систем ОДУ, разработанный в 2006 году Недялковым Н. С на алгоритмическом языке С++. В отличие от традиционных решателей, которые вычисляют приблизительные решения, этот решатель доказывает, что существует единственное решение задачи, а затем строит строгие границы, которые гарантированно содержат его.

Библиотека является преемником библиотеки VNODE (Validated Numerical ODE), разработанной Недялковым Н. С. Отличительной особенностью данного решателя является то, что он полностью посвящен «грамотному программированию». Грамотное программирование - это стиль написания программ, при котором программа рассматривается не как последовательность инструкций для компьютера, а как литературное произведение. Таким образом, программист при написании программы формально описывает действия, которые он ожидает от компьютера, вставляя в соответствующие места код на языке программирования. Данная концепция предложена Кнутом Д. в 1984 году.

На первом этапе используется метод HOE, а во втором - метод Эрмита - Обрешкова. VNODE-LP имеет переменный шаг интегрирования и постоянный порядок.

Методы модели Тейлора

Начиная с 1990-х годов профессором Берзом М. и его командой были разработаны методы модели Тейлора, которые сочетают интервальную арифметику с символьными вычислениями [44]. В этих методах основным типом данных является так называемая модель Тейлора, которая представляет собой полином некоторой степени с интервальным остатком:

Решение интервальных систем ОДУ ищется в виде модели Тейлора относительно интервальных начальных условий. Все арифметические действия в методах заменяются соответствующими операциями над полиномами, в результате чего в конечный момент времени решение представляется в виде полинома относительно интервальных параметров и некоторого интервального остатка.

Уже начиная с третьего шага в процессе вычислений появятся степени больше второй, которые будут «уходить» в интервальный остаток. Полученное таким способом решение не является гарантированным, так как оно не учитывает погрешность метода Эйлера. В оригинальном методе происходит аналитическое разложение решения в ряд Тейлора и вычисление интервальной оценки остаточного члена. Поэтому полученное таким способом решение гарантированно содержит все решения исходной системы ОДУ.

В целом использование арифметики моделей Тейлора вместо классических интервальных арифметик существенно снижает эффект обертывания, особенно при интегрировании нелинейных систем ОДУ.

Библиотека COSY Infinity

Библиотека COSY Infinity [47] разрабатывается в Мичиганском университете профессором Берзом М. и его командой. Это система для проведения различных современных научных вычислений. Она состоит из следующих частей:

1.   Набор расширенных и оптимизированных типов данных:

•     Дифференциальные алгебраические типы для многомерного исследования ОДУ, потоков и дифференциальных уравнений в частных производных высокого порядка. Здесь имеется поддержка автоматического дифференцирования высокого порядка.

•     Тип модели Тейлора для строгих вычислений высокого порядка. Разнообразные инструменты - в частности, инструменты для ограничения роста остаточного члена, инструменты для проверки ограничений и т. д.

2.   Скриптовый язык COSYScript, в котором используются описанные выше типы. Он объектно ориентирован и поддерживает полиморфизм, имеет компактный и простой синтаксис, компилируется и выполняется на лету.

3.    Интерфейсы для C, F77, C++ и F90 для использования типов во внешних программах. 4. Различные прикладные пакеты с использованием типов данных COSY, включая физику луча.

К сожалению, в текущей версии библиотеки COSY Infinity 10.1 (2018 год) модель Тейлора не поддерживается и при этом доступ к более ранним версиям отсутствует. В связи с этим выполнить прямое сравнение с данным программным комплексом не представляется возможным. Однако в работе [48] приводится сравнение библиотеки RiOT с COSY-VI на представительном наборе задач. Поэтому при сравнении с библиотекой RiOT будет выполнено косвенное сравнение с библиотекой COSY.

Библиотека RiOT

RiOT - это свободная программа на языке C++ для интегрирования систем ОДУ с интервальными начальными условиями, последняя версия - 2008 года [48]. В ней реализованы модель Тейлора, предложенная Берзом М. и Макино К., а также механизм уменьшения накопления ошибок интегрирования Shrink Wrapping [70, 71], который позволяет выполнять интегрирование на длительные периоды. Идея механизма заключается в том, что за счет варьирования коэффициентов полинома удается как бы «спрятать» интервальный остаток в полином, где уже работает неинтервальная арифметика.

Библиотека FlowStar

Библиотека FlowStar [50] - это инструмент для достоверного моделирования гибридных динамических систем с интервальными параметрами, разработанный на языке С++, последняя версия - 2017 года. По значению интервальных параметров, натурального числа m и гибридной системе A , которая моделируется гибридным автоматом, FlowStar вычисляет конечный набор моделей Тейлора, содержащий в себе все состояния A , которые достижимы не более чем за m шагов.

Библиотека состоит в основном из двух модулей: вычислительной библиотеки и алгоритмов высокого уровня. В первый модуль входят реализации интервалов и интервальных арифметик, а также модель Тейлора. Во втором модуле реализованы методы, которые используются в анализе достижимости. Текущая версия FlowStar поддерживает гибридные системы, включающие в себя следующие компоненты:

•     Непрерывные динамические системы, которые задаются с помощью ОДУ с интервальными начальными условиями и параметрами.

•     Условия перехода, которые можно определять в виде системы полиномиальных неравенств. • и т.д.

Сравнение методов и реализаций

На рис. 4 показано множество решений системы в различные моменты времени. Для начальной точки x=1, y=3 период вращения равен T = 5, 488138468035 , о чем свидетельствует совпадение центров множеств в начальный момент времени и при t= T. Из- за того, что для остальных начальных точек, содержащихся в интервальных начальных условиях, период вращения другой, происходит вытягивание множества.

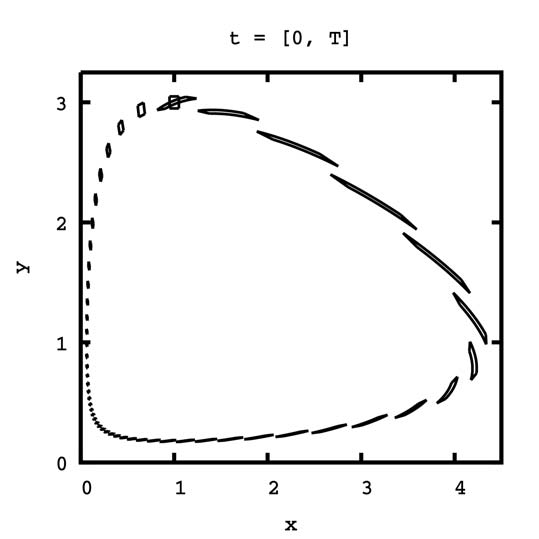
Рис. 4. Один период вращения множества решений системы

В таблице 1 и на рис. 5 приведено сравнение результатов, полученных разными программными комплексами. Библиотеки AWA и VNODE-LP практически не компенсируют эффект обертывания, и уже с момента t > 4,5 его влияние оказывается существенным и решения расходятся. Отметим, что по вычислительным затратам библиотека VNODE- LP наиболее эффективная.

Таблица 1

Сравнение результатов решения системы в момент времени 0,8T

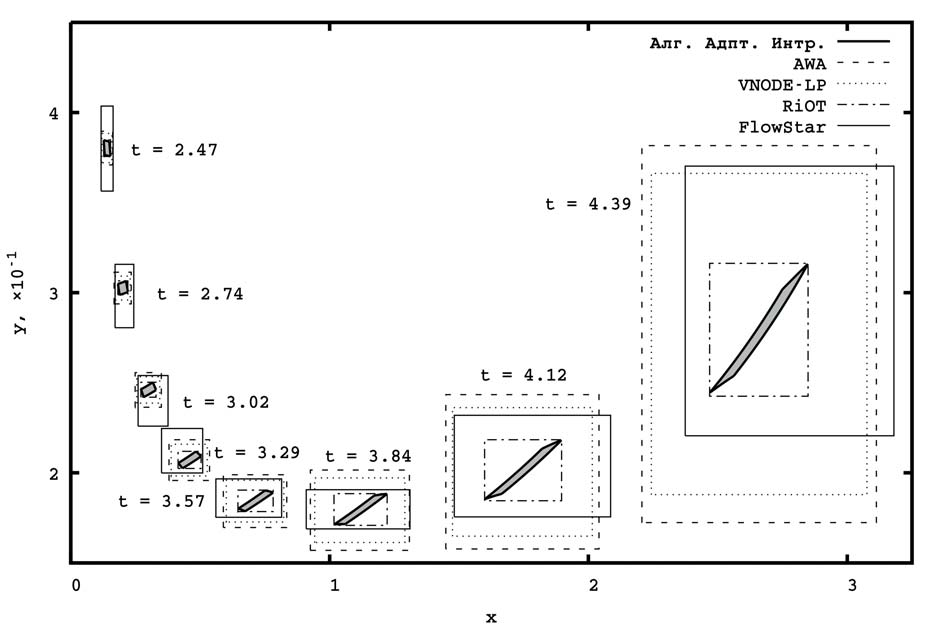
Рис. 5. Сравнение решений системы , полученных различными библиотеками, в различные моменты времени

В таблице 2 приведено сравнение с библиотекой COSY-VI. Здесь и далее время работы COSY-VI оценивается относительно библиотеки RiOT, так как в работе [48] имеется их сопоставление. В таблице 3 и на рис. 6 приведено сравнение решений системы в момент времени t = 14,56 . Здесь наблюдается сильное завышение получаемых оценок решений.

Таблица 2

Сравнение результатов решения системы в момент времени T

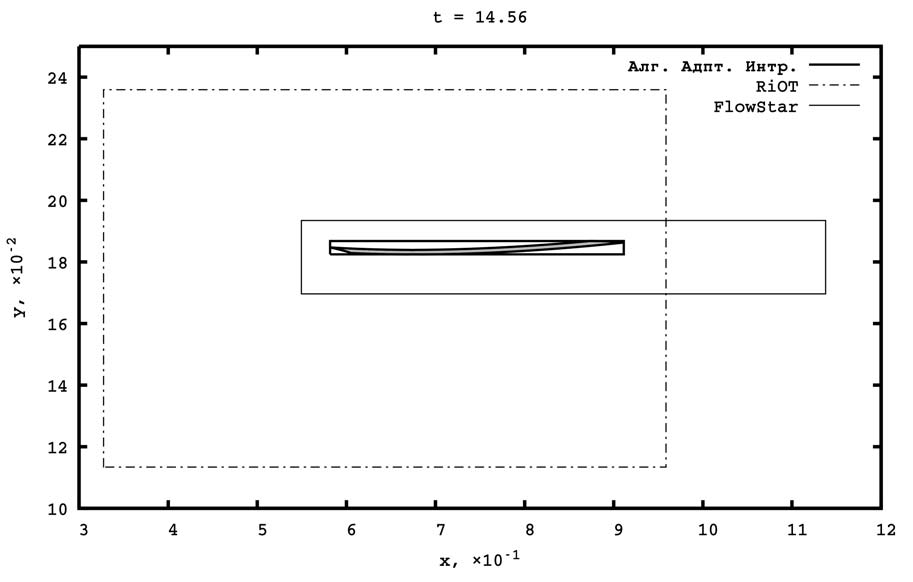
Рис. 6. Оценки решений системы различными библиотеками

На рис. 7 приведена иллюстрация решения, полученного библиотекой FlowStar. Интервальный остаток (i) существенно больше полиномиальной части решения, и уже при t - 16 библиотека аварийно завершает расчет.

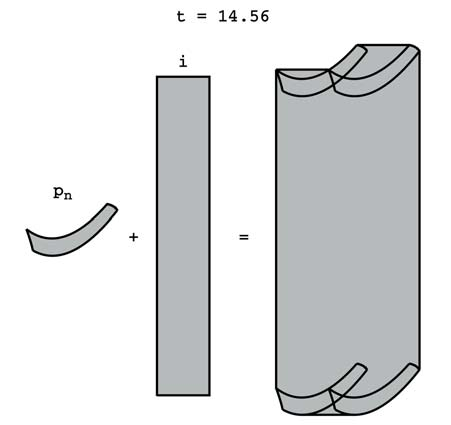
Рис. 7. Модель Тейлора. Решение системы , полученное FlowStar

Рассмотрим систему ОДУ:

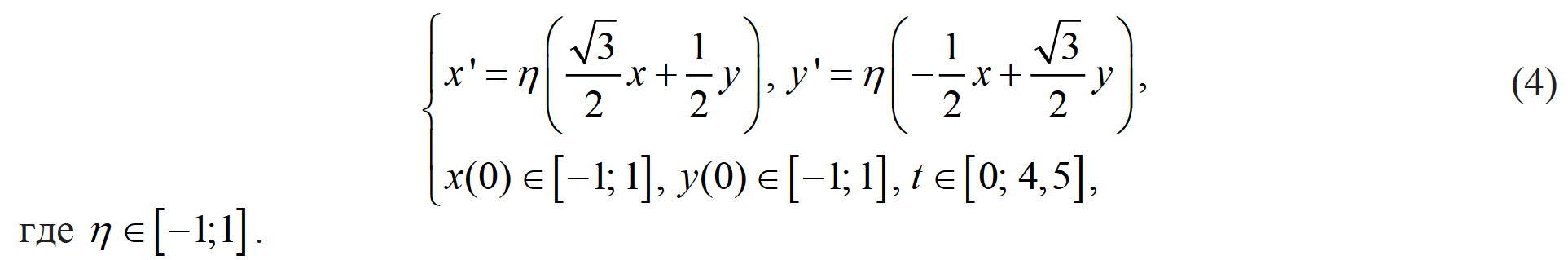
На рис. 8 и рис. 9 показано множество решений исходной системы ОДУ в различные

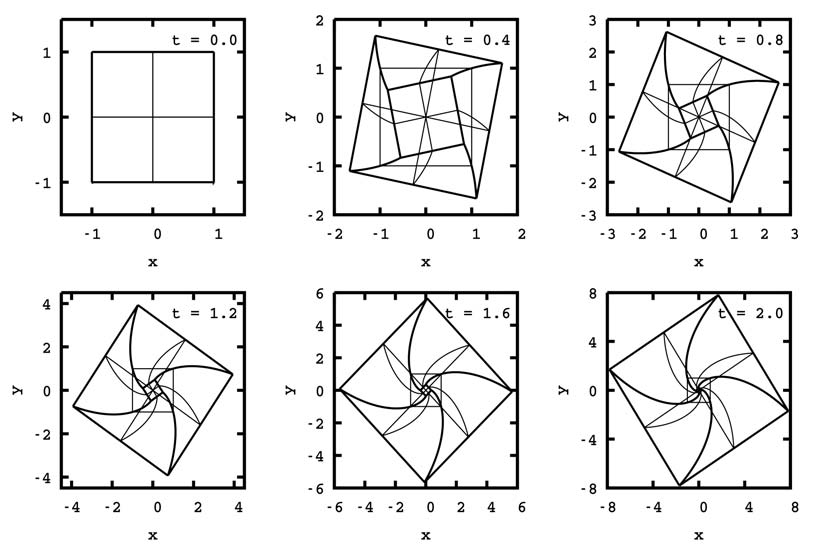
Рис. 8. Множество решений системы в различные моменты времени

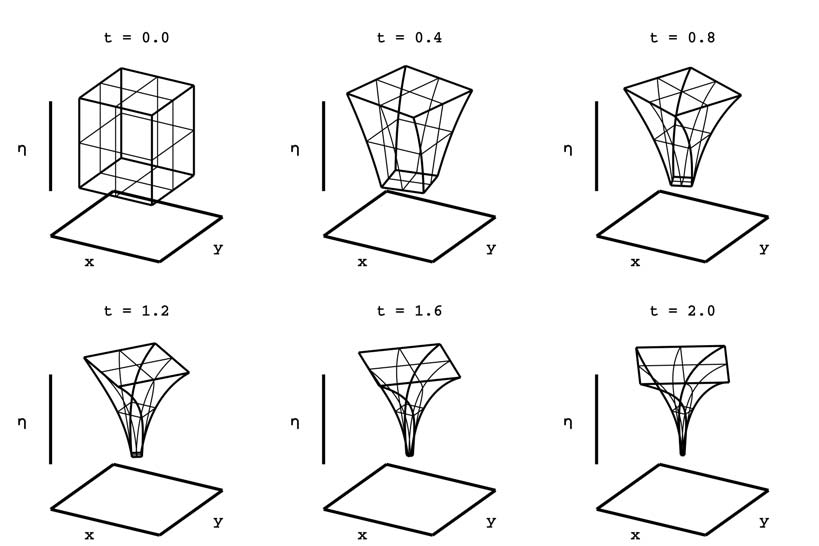
Рис. 9. Множество решений системы в трехмерном пространстве

Сравнение результатов решения системы в момент времени 14,56

Здесь наблюдается закручивание множества в спиралевидную воронку. Для алгоритма адаптивной интерполяции это приводит к постоянному увеличению плотности сетки по измерению ц. В плоскости x, у при каждом конкретном значении ц соответствующие сечения множества претерпевают линейные деформации растяжения и вращения.

Библиотеки AWA и VNODE-LP работают быстрее всех (таблица 4), но при этом они дают очень завышенные оценки решений и спустя некоторое время аварийно завершают расчет.

На рис. 10 представлено сравнение решений, полученных указанными библиотеками.

Рис. 10. Сравнение решений системы , полученных различными библиотеками, в различные моменты времени

Таблица 4

Сравнение результатов решения системы в момент времени 0,8

В целом, как и в предыдущих примерах, библиотека FlowStar проявляет себя лучше, чем AWA и VNODE-LV, с точки зрения получаемых результатов. Но тем не менее из-за того, что метод, реализованный в ней, подвержен накоплению ошибок, спустя некоторое время от начала интегрирования получаемые интервальные оценки начинают расходиться.

Заключение

Выполнен обзор существующих библиотек и реализованных в них методов моделирования динамических систем с интервальными параметрами. Рассмотрены доступные библиотеки программ гарантированных вычислений AWA, VNODE-LP, COSY Infinity, RiOT, FlowStar, а также авторский алгоритм адаптивной интерполяции. Методы, реализованные в библиотеках AWA и VNODE-LP, просты и нетребовательны в плане вычислительных ресурсов, но эффективны в задачах, где интервалы не слишком велики или где нелинейность системы ОДУ проявляется слабо. Библиотеки COSY Infinity, RiOT и FlowStar основаны на символьно-интервальных вычислениях и область их применения значительно шире по сравнению с библиотеками AWA и VNODE-LP. Однако они тоже имеют тенденцию к завышению интервальных оценок. За счет использования принципиально другого подхода к построению решений алгоритм адаптивной интерполяции не подвержен накоплению ошибок, определяет границы решений с контролируемой точностью и работает значительно быстрее аналогов.