Дискриминантный анализ на основе статистик Кохонена

В статье приводится описание нового подхода к дискриминантному анализу, опирающемуся на нейросети Т. Кохонена. Рассматривается алгоритм анализа и его преимущества.

Введение

В современных методах многомерного анализа данных дискриминантный анализ занимает важное место, представляя собой эффективное средство для решения задач классификации. Определение межгрупповых различий помогает выяснить, насколько эффективно набор используемых переменных способен разделять объекты обучающей выборки, и какие из этих переменных обладают наибольшей информативностью, что является одной из задач, решаемых средствами дискриминантного анализа. В данной работе речь пойдет о другой задаче - предсказании значений группирующего фактора для исследуемой группы наблюдений.

Несмотря на свою популярность, традиционные методы дискриминантного анализа несовершенны из-за существования в алгоритме их работы ограничений, обусловленных известными предположениями. Одно из них заключается в том, что исходные данные для получения корректного результата должны описываться многомерным нормальным распределением, что может стать препятствием при работе с реальными наблюдениями. Стоит также отметить чувствительность анализа к выбросам: единичные аномалии или ошибки измерения могут значительно повлиять на оценки и результаты классификации.

Карты Кохонена

Самоорганизующаяся карта Кохонена (Self-Organizing Map — SOM) представляет собой нейронную сеть без учителя, предназначенную для визуализации и кластеризации данных. Эта структура, предложенная финским ученым Т. Кохоненом в 1982 году, используется для проецирования многомерных данных в пространство более низкой размерности, чаще всего двумерное. SOM также применяется для решения задач моделирования, прогнозирования, выявления наборов независимых признаков и поиска закономерностей в больших объемах данных. В своем основном варианте SOM создает граф подобия входных данных.

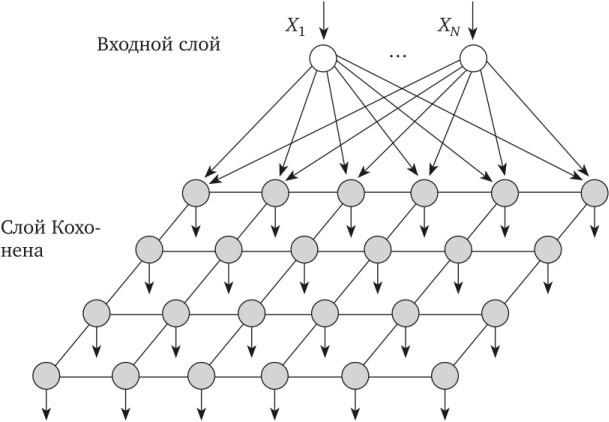
Рис. 1 Структура самоорганизующейся карты Кохонена.

Карта представляет собой сетку из узлов, которые соединены между собой связями. Сетка может быть прямоугольной или гексагональной формы. Также определяется количество нейронов в сети. Каждый узел описывается двумя векторами. Первый вектор - вектор веса, имеет такую же размерность, что и входные многомерные данные. Второй вектор - координаты узла на карте. Перед началом обучения необходимо инициализировать весовые коэффициенты нейронов. Затем для каждого входного образца происходит поиск ближайшего нейрона на основе Евклидова расстояния между векторами весов нейрона и входным образцом. Выбранный нейрон и его соседи на карте проходят через процесс обновления весов. Веса нейрона и его соседей изменяются с целью приближения к входному образцу. Это позволяет картам перестраиваться и адаптироваться к статистическим свойствам входных данных. В процессе обновления весов используются два основных механизма: конкуренция и кооперация. Конкуренция заключается в выборе победившего нейрона, который наиболее близок к входному образцу. Кооперация проявляется в том, что веса победившего нейрона и его соседей обновляются в направлении входного образца. Этот процесс обновления весов повторяется для всех входных образцов в несколько итераций. По мере обучения сетки происходит снижение ошибки и улучшение качества представления данных на карте. По завершению обучения, каждый нейрон на карте будет представлять определенный класс или категорию, а распределение нейронов на карте будет отражать статистическую структуру данных.

Описание метода

Для наглядного представления этапов дискриминантного анализа и их изменений приведены блок-схемы классического и нового варианта анализа.

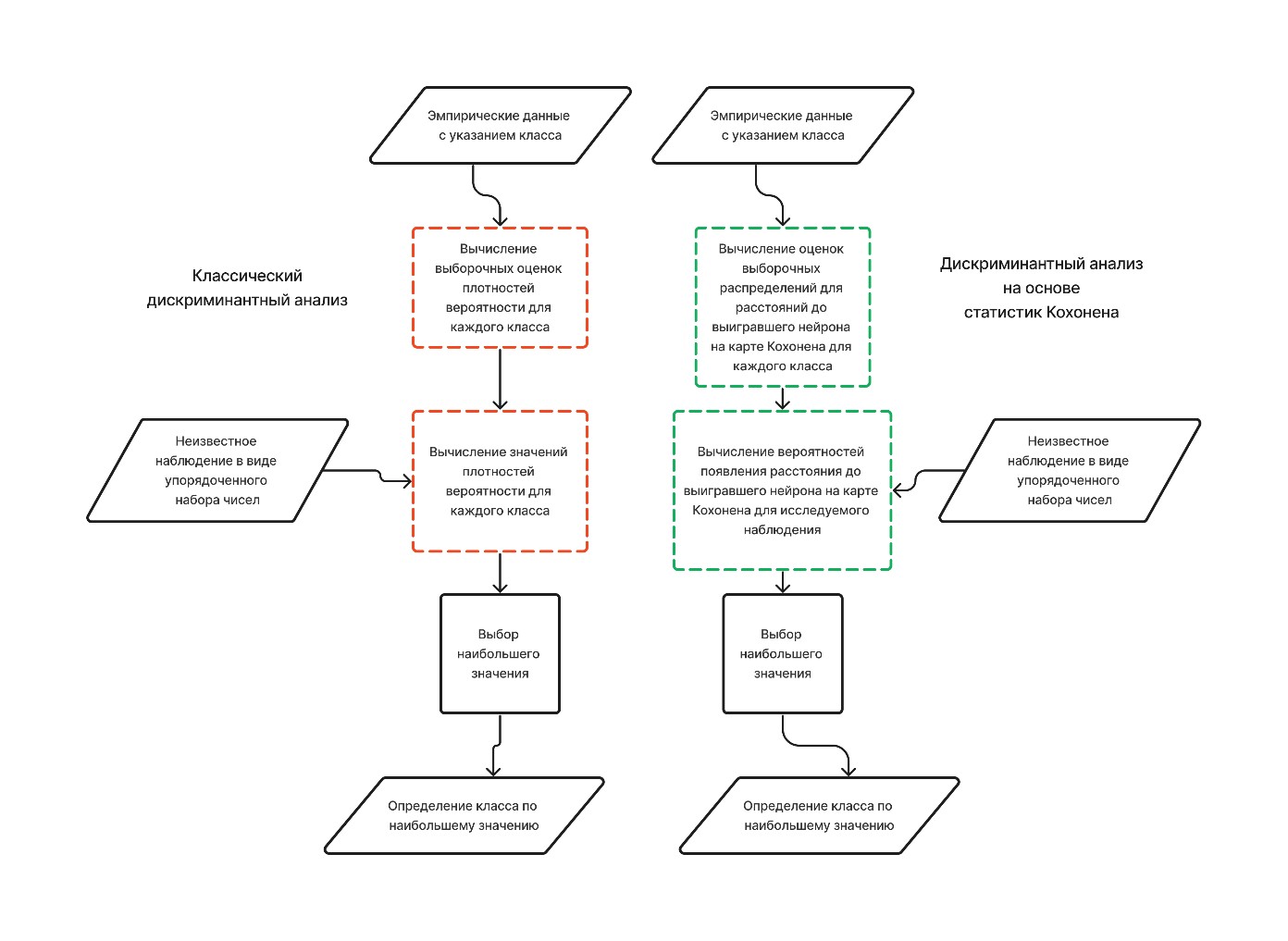
Рис. 2 Блок-схемы для классического и нового варианта дискриминантного анализа.

Суть нового подхода заключается в том, чтобы обучить для каждого имеющегося в обучающей выборке класса отдельную карту. Такой подход позволяет четко проследить, что каждая из них организуется на своих данных и какие образцы ей соответствуют. Это дает возможность проводить классификацию новых эмпирических наблюдений, опираясь на их близость к нейронам на каждой из обученных карт. Кроме того, такое разделение упрощает интерпретацию результатов и дает более понятное представление о том, как классы представлены на карте.

Выбор главного параметра - размерности карты SOM - зависит от количества объектов в обучающей выборке и количества априорно известных классов. Так как в проведенном исследовании инициализация карты происходит случайными значениями из выборки, важно иметь достаточное количество нейронов, чтобы хорошо представить структуру данных. Анализ итоговой статистики при переборе различных значений размера карты показал, что лучший результат соответствует использованию 5-12 нейронов на каждый класс. При выборе размерности карты SOM следует учитывать этот критерий, чтобы достичь баланса между адекватностью результатов анализа и ресурсоемкостью.

После обучения всех карт можно перейти к определению вероятностей принадлежности объекта к конкретному классу. Для этого используется тестовая выборка значений каждого априорного класса. Для объекта тестовой выборки вычисляется евклидово расстояние до выигравшего нейрона на соответствующей этому объекту карте. После вычисления расстояний до выигравших нейронов для каждого класса на основе этих расстояний строится гистограмма. Количество её интервалов группировки определяется правилом Стёрджеса — это эмпирическое правило для определения оптимального количества интервалов, на которые следует разбить диапазон значений случайной величины при построении гистограммы плотности её распределения:

.

Гистограмма дает графическое представление распределения значений расстояний для каждого класса. Частоты попадания в интервалы группировки нормируются таким образом, чтобы сумма для каждого класса составляла единицу. Нормирование гистограммы позволяет получить вероятностное распределение принадлежности объектов к классам.

Для оценки работы классификатора на объекте из тестовой выборки необходимо вычислить расстояния для каждой карты между этим объектом и выигравшими нейронами. Затем, используя построенные гистограммы, можно определить вероятностную оценку принадлежности объекта к каждому из известных классов. После нормировки получаются значения, которые отражают степень близости объекта к каждому классу — эти вероятностные оценки позволяют понять, к какому классу более или менее вероятно принадлежит объект. Принадлежность определяется максимальной вероятностью.

Иллюстрация работы алгоритма

Для иллюстрации применения нового подхода была использована традиционная для курсов многомерного статистического анализа выборка ирисов Фишера, содержащая информацию о трех видах цветков. Она состоит из набора измерений четырех признаков: длины и ширины чашелистиков и лепестков. Каждый образец в выборке имеет соответствующую метку класса, обозначающую вид ириса: setosa, versicolor или virginica. Это позволяет проводить классификацию ирисов на основе их характеристик.

Сначала было обучено 3 карты Кохонена: карта для класса setosa обучается только на образцах этого класса, карта для класса versicolor - только на образцах versicolor, и аналогично для карты класса virginica. Размерность каждой карты составила 3, то есть 9 нейронов на карту.

Для получения гистограмм был проведен анализ 3 тестовых выборок — выборка каждого класса проверялась на соответствующей ей карте. В результате чего получены расстояния до выигравших нейронов на каждой карте, по которым были построены гистограммы. Затем они нормируются.

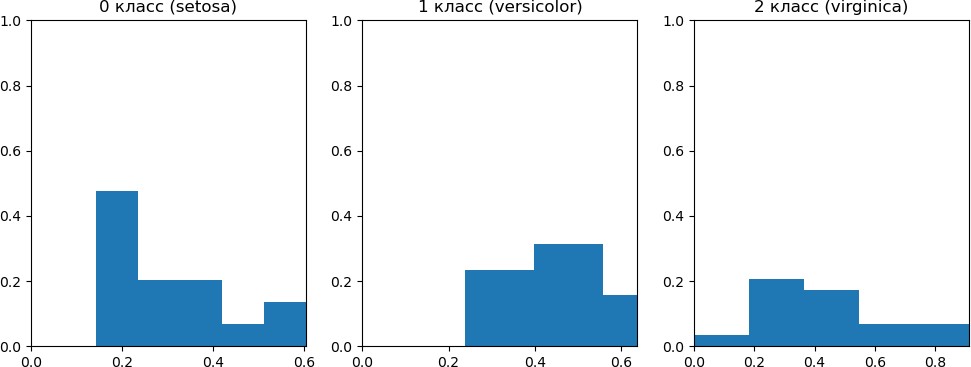
Рис. 3 Диаграммы для классов setosa, versicolor, virginica.

Исходя из полученной статистики, можем определить правильно ли объект был отнесен к классу, ведь в тестовой выборке мы знаем, к какому классу он действительно принадлежит. Результаты представлены в виде матрицы классификаций.

,

Полный алгоритм, примененный к ирисам Фишера, реализован на языке программирования Python. После неоднократных выполнений программы, изменений параметров карт и их размеров стало ясно, что алгоритм выполняет поставленную задачу строго не хуже, а, как правило, лучше (зависит от случайной инициализации нейронов) дискриминантного анализа Фишера. Помимо определения класса поступающего на вход объекта, программа даёт оценку вероятности принадлежности к этому и другим классам.

Заключение

В статье представлен новый непараметрический вариант дискриминантного анализа, особенностями которого являются:

• использование для выбора классов самоорганизующихся карт Кохонена;
• получение вероятностной оценки принадлежности к классам;
• устойчивость к выбросам в эмпирических данных.

Преимуществом разработанного подхода является отсутствие априорных предположений о распределении исследуемых эмпирических данных.

1. Кохонен Т. Самоорганизующиеся карты, пер. 3-го англ. изд. 2-е изд. (эл.), М. БИНОМ. Лаборатория знаний, 2014.
2. Куравский Л. С., Баранов С. Н. Компьютерное моделирование и анализ данных. Конспекты лекций и упражнения: Учеб. пособие. – М.: РУСАВИА, 2012. С. 62-65, 108
3. Воронцов К. В. Математические методы обучения по прецедентам (теория обучения машин), С. 9, 42 URL: https://www.kaznu.kz/content/files/pages/folder23376/Voron-ML-1.pdf
4. Воронов, М. В. Системы искусственного интеллекта: учебник и практикум для вузов / М. В. Воронов, В. И. Пименов, И. А. Небаев. — 2-е изд., перераб. и доп. — Москва: Издательство Юрайт, 2023.
5. StatSoft. Электронный учебник по статистике // Дискриминантный анализ. URL: http://statsoft.ru/home/textbook/modules/stdiscan.html
6. Sturges H. The choice of a class-interval. J. Amer. Statist. Assoc., 1926 P. 21, 65- 66.