Применение статистик m* и d* для оценки качества данных психологического исследования с помощью закона Бенфорда (на примере измерения времени реакции)

Н.И. Колачев

doi:10.17759/mda.2024140202

Введение

Высокое качество собранных данных имеет ключевое значение для формулирования выводов во многих эмпирических исследованиях. На достоверность собираемых данных могут влиять различные факторы: несовершенства измерительного инструмента, методические погрешности, отсутствие стандартизации процедуры сбора данных и многое другое. Особого внимания требуют результаты измерения нефизических величин (например, мотивации, когнитивных процессов и пр.), которые не поддаются непосредственному, прямому измерению, и, как правило, подвержены влиянию флуктуаций в поведении респондента (испытуемого).

В части исследования качества многое сделано для оценки достоверности данных, собираемых опросно-анкетными методами. К примеру, хорошо известно, как справляться с таким фактором недостоверности самоотчётных данных, как социальная желательность [Осин, 2011]. Более того, разработаны специальные подходы для измерения характеристик личности, которые могут подвергаться искажениям при самоотчёте. К числу таких подходов относятся методы поведенческих сценариев [Peng, 1997], якорных виньеток [Primi, 2016], сценарных шкал [Antipkina, 2020].

При этом необходимо констатировать, что на сегодняшний день не предложены методы анализа достоверности данных о времени реакции, что делает настоящую работу особенно актуальной, ведь измерение времени реакции является основой когнитивной психологии [Психология высших когнитивных, 2004].

Время реакции

Время реакции широко распространено и обычно используется в науках о поведении для оценки и моделирования когнитивных процессов, чаще всего внимания [Dutilh, 2019]. Под временем реакции понимают временной интервал между появлением какого-либо стимула и ответом (реакцией) на этот стимул со стороны испытуемого [Карпенко, 1998]. Обычно измеряется в миллисекундах (мс). В исследованиях с использованием показателя времени реакции выделяют три вида возможных реакций [Зайцев, 2002]:

Простая сенсомоторная реакция (реакция на появление любого стимула);
Дифференцировочная реакция простого выбора (реакция на стимулы определенного типа и игнорирование всех остальных);
Дифференцировочная реакция сложного выбора (ответ на каждый тип стимула должен сопровождаться определенной реакцией).

На протяжении многих лет время реакции служило основой для значимых открытий в экспериментальной, когнитивной психологии, нейрофизиологии, таких как эффект Струпа [Stroop, 1935], аффективный прайминг [Zhang, 2012] и др. По сей день вопросы работы со временем реакции являются актуальными для исследователей. Так, известно, что распределение времени реакции во многих исследованиях имеет правостороннюю асимметрию [Whelan, 2008], поэтому в качестве меры центральной тенденции рекомендуют использовать медиану или моду, а не среднее арифметическое. Кроме того, ряд исследователей говорит о лог-нормальности распределения времени реакции, то есть логарифм времени реакции имеет нормальное распределение [Marmolejo-Ramos, 2015]. Некоторые исследователи указывают, что распределение времени реакции подчиняется так называемому экс-гауссовскому распределению (смесь гауссовского и экспоненциального) [Whelan, 2008].

Основным фактором, влияющим на качество данных о времени реакции, является невыполнение испытуемым поставленной задачи. Если испытуемый хаотично, бессистемно реагирует на стимулы (например, нажимать клавиши на клавиатуре компьютера, ведь большая часть современных исследований проводится в компьютерном формате, даже онлайн [R Core Team, 2021]), то исследователи получают недостоверные данные, ничего не свидетельствующие об особенностях познавательных процессов испытуемого. Существующие рекомендации по работе с данными о времени реакции лишь предлагают способы «подгонки» данных под существующие статистические методы, как, например, исключение выбросов по правилу «±2 стандартных отклонения», или методы работы с пропущенными данными [Lachaud, 2011]. Все эти рекомендации не позволяют судить о достоверности собранных данных. В связи с этим возникает острая необходимость в поиске способов проверки качества получаемых или генерируемых данных. Одним из вариантов может выступить использование закона Бенфорда.

Закон Бенфорда

Закон Бенфорда – известная закономерность в области математики. Она заключается в том, что в некотором большом наборе числовых данных первая значащая цифра, не включая ноль, встречается с частотой, равной

\log (1 + \frac{1}{k})

, где k – первая значащая цифра от 1 до 9 [Куликова, 2004]. Закономерность была получена Фрэнком Бенфордом, сотрудником известной компании «General Electric», на примере большого числа данных: длин рек, численности городов США, смертности и пр. [Benford, 1938]. Позднее этот закон нашёл отражение во многих областях человеческой деятельности. К примеру, закономерность Бенфорда используют для выявления подлога в бухгалтерской отчетности и оценки качества отчетности о движении денежных средств [Попина, 2016], фальсификаций на выборах, подсчёта количества числительных в статьях [Зенков, 2015], достоверности данных профилактического скрининга в области медицины [Старунова, 2022]. Поскольку закономерность Бенфорда воспроизводится на разнообразных данных, некоторые авторы называют её фундаментальным законом природы [Лонэ, 2022].

Стоит отметить, что не все переменные подчиняются закону Бенфорда. Так, считается, что «почтовые индексы, выигрышные номера в лото и рулетку, номера телефонов и любые объемы данных, размер которых не достаточен для применения статистических методов» [Кувакина, 2013, с. 76]. Кроме того, время реакции в пределах от 100 до 200 мс может быть, например, результатом быстрой догадки. Такие быстрые реакции легко выявляются, и их обычно исключают из анализа [Whelan, 2008]. При этом такие значения встречаются в распределении реже, чем, допустим, значения в интервале от 400 до 500 мс, что говорит о низкой согласованности первой значащей цифры исходных данных о времени реакции с законом Бенфорда, поскольку, согласно этому закону, цифры 1 и 2 встречаются чаще, чем 4 и 5.

Другой существенной проблемой применения закона Бенфорда является подбор подходящих методов оценки согласия эмпирических данных с этим законом. Тестирование гипотезы о соответствии эмпирического распределения значащих цифр закону Бенфорда обычно происходит методом хи-квадрата или с помощью критерия Колмогорова [Morrow, 2014]. Как полагает Джон Морроу, эти тесты являются достаточно консервативными, то есть довольно часто не позволяют отклонить нулевую гипотезу в ситуации, когда данные не согласуются с законом Бенфорда (другими словами, имеют высокую вероятность ошибки II рода). В связи с этим возникла необходимость разработки новых тестов для проверки гипотезы о соответствии данных этому закону.

Модификации статистических тестов согласия с законом Бенфорда

Решением проблемы консервативности статистических тестов занялся Джон Морроу [Morrow, 2014]. В своей работе он доказал следующую теорему:

пусть X – непрерывная случайная величина, B – закон Бенфорда, тогда

\forall ε > 0 \exists γ^{} : \forall γ \geq γ^{} | x^{γ} - B | < ε,

где

x^{γ}

– стандартизированные значения из различных распределений (например, нормального, лог-нормального, экспоненциального и др.), возведённые в степень

γ

. В оригинальной статье вместо

γ

фигурирует

α

, однако, чтобы не путать этот параметр с уровнем значимости, который в статистике обозначается как α, было принято решение использовать другую греческую букву. По итогам анализа Дж. Морроу пришёл к выводу, что 10-е степени (

γ = 10

) стандартизированных значений имеют высокое согласие с законом Бенфорда. Однако остаётся неясным, почему выбрана именно 10-я степень.

Кроме того, вместо классических тестов на однородность, таких как хи-квадрат или тест Колмогорова, он предложил критические значения для двух тестов (

m^{}

и

d^{}

), предназначенных для проверки соответствия эмпирического распределения первой значащей цифры закону Бенфорда:

m^{} = \sqrt{n} ∙ \max_{d \in {1, \dots,9}} \begin{matrix} | P (первая значащая цифра X = d) - \log_{10} (1 + \frac{1}{d}) | \end{matrix}

\begin{matrix} d^{} = \sqrt{n} ∙ {[\sum_{d \in {1, \dots,9}} {(P (первая значащая цифра X = d) - \log_{10} (1 + \frac{1}{d}))}^{2}]}^{\frac{1}{2}} \end{matrix}

где

n

– объём выборки,

\log_{10} (1 + \frac{1}{d})

– закон Бенфорда. В статистической литературе статистку

m^{}

называют расстоянием Чебышёва, а

d^{}

– евклидовым расстоянием [Campanelli, 2024].

Также учёный показал, что предложенные им статистические тесты достигают достаточной мощности при объёме выборки, превышающем 80 наблюдений (при уровне значимости α=0.01).

Необходимо сказать, что психологические исследования, в которых фигурирует время реакции в качестве основной переменной, довольно часто проводятся на скромных по объёму выборках (как правило,

n < 50

). К примеру, Маршалек и коллеги [Marszalek, 2011] в рамках анализа множества публикаций показали, что средний размер выборки в серьёзном психологическом исследовании составляет 40 человек. Этому есть разумное объяснение. С одной стороны, это обусловлено отсутствием необходимости в больших объёмах, так как небольшой объём выборки компенсируется достаточным количеством производимых измерений у одного человека; с другой стороны, объясняется трудозатратностью самой процедуры сбора данных, так как экспериментальные когнитивные исследования занимают довольно много времени (в среднем 1–1,5 часа) и требуют от участников немалых усилий. Однако несмотря на сложившуюся практику, вопрос проверки качества данных остаётся ключевым, следовательно, даже маленькие по объёму выборки данных должны подвергаться анализу на предмет качества.

В связи с этим целью исследования является изучение свойств статистик

m^{}

и

d^{}

при скромных объёмах выборки (

10 \leq n \leq 70

) на основе данных о времени реакции. Для достижения поставленной цели были сформулированы следующие задачи:

1.Изучить, различаются ли значения $m^{}$ и $d^{}$ в зависимости от объёма выборки;
2.Исследовать, зависят ли значения статистик $m^{}$ и $d^{}$ от степени, в которую возводят стандартизированное значение времени реакции, при контроле объёма выборки;
3.Установить критические значения статистик $m^{}$ и $d^{}$ для небольших по объёму выборок ( $10 \leq n \leq 70$ ) на основе симуляций из лог-нормального распределения;
4.Проверить функциональность установленных критических значений на экспериментальном (эмпирическом) примере.

Для решения поставленных задач сначала проведено симуляционное исследование. Был сгенерирован набор данных о времени реакции следующих объёмов (n): 10, 20, 30, 40, 50, 60 и 70. В качестве функции для генерации данных выбрана лог-нормальная с такими параметрами:

μ = 5,984

,

σ = 0,1245

, что соответствует среднему времени реакции 400 мс и стандартному отклонению 50 мс. Эти значения часто используются в симуляционных исследованиях [Whelan, 2008]. Затем сгенерированные значения были стандартизированы по следующей формуле:

\begin{matrix} \frac{x_{i} - μ}{σ} \end{matrix}

где

x_{i}

– i-е значение переменной из лог-нормального распределения. Далее стандартизированные значения были возведены в k-ю степень с шагом h = 5, начиная со второго элемента;

k \in {1,5,10, \dots,100}

. Именно у возведённых в k-ю степень стандартизированных значений изучалось распределение первых значащих цифр с помощью статистик

m^{}

и

d^{}

*, описанных выше. В рамках симуляционного исследования изучалось поведение

m^{}

и

d^{}

. Для каждого объёма выборки (n) симулировалось 105 репликаций.

Прежде чем произвести поиск критических значений на основе данных симуляций, были проверены различия в средних значениях статистик

m^{}

и

d^{}

в разрезе разных объёмов выборок, а также в зависимости от степени числа. Изучение различий в средних в разрезе разных n проходило с помощью дисперсионного анализа (ANOVA). Модель в матричном виде выглядит следующим образом:

\begin{matrix} Y = Xβ + e \end{matrix}

где

Y

– вектор зависимой переменной размера

n \times 1

,

X

– вектор независимой качественной переменной размера

n \times d

,

β

– вектор неизвестных параметров размера

d \times 1

, e – вектор остатков (ошибок) размера

n \times 1

.

Дисперсионный анализ основан на вычислении межгрупповой и внутригрупповой дисперсии и расчёте статистики Фишера (F-статистики):

\begin{matrix} D_{меж .} = \frac{\sum_{i = 1}^{k} n_{i} \cdot {(\bar{x_{i}} - \bar{x})}^{2}}{k - 1} \end{matrix}

\begin{matrix} D_{внутр .} = \frac{\sum_{i = 1}^{k} D_{i}}{k} \end{matrix}

\begin{matrix} F = \frac{D_{меж .}}{D_{внутр .}} \end{matrix}

где

n_{i}

– объём выборки i-ой группы,

\bar{x_{i}}

– среднее i-ой группы,

\bar{x}

– общее среднее,

k

– количество групп,

D_{i}

– дисперсия i-ой группы.

Зависимость статистик от степени числа изучалась с помощью корреляции Спирмена (

ρ

):

\begin{matrix} ρ = 1 - \frac{6 \sum d_{i}^{2}}{n (n^{2} - 1)} \end{matrix}

где

d_{i}^{2}

– разница рангов i-го наблюдения,

n

– количество наблюдений. Выбор именно этого коэффициента корреляции обоснован тем, что он учитывает не только линейные, но монотонно убывающие или монотонно возрастающие связи или зависимости (в отличие от коэффициента Пирсона).

Затем на основе распределения статистик

m^{}

и

d^{}

произведено отсечение по 90-му, 95-му и 99-му перцентилям, поскольку

m^{}

и

d^{}

являются односторонними критериями, что соответствует критическим значениям для

α = 0,10

,

α = 0,05

и

α = 0,01

. Полученные критические значения сравнивались с асимптотическими критическими значениями, представленными в работе Джона Морроу [Morrow, 2014].

Симуляционное исследование дополнено экспериментальным (эмпирическим). В рамках этого исследования два респондента прошли когнитивный тест (тест Струпа), который заключается в том, что испытуемые нажимают нужные клавиши на клавиатуре компьютера в зависимости от цвета краски появившегося слова по следующему правилу: «←» – красный, «↑» – жёлтый, «↓» – зелёный, «→» – синий. Причём появившееся слово обычно означает цвет, тем самым возникает семантическая интерференция. В ходе выполнения теста фиксируется время реакции и правильность нажимания клавиши. Некоторые стимулы являлись нейтральными (например, вместо слова показывался набор символов «XXXXX»). На рисунке 1 представлен пример стимула.

Рис. 1. Пример стимула в тесте Струпа.

Первый респондент (контрольный случай) выполнял тест, согласно стандартной инструкции: «Ваша задача – как можно быстрее и точнее реагировать на окраску слова ведущей рукой. Для ответа необходимо использовать стрелки на клавиатуре: ВЛЕВО – для красного, ВВЕРХ – для желтого, ВНИЗ – для зелёного и ВПРАВО – для синего». Второй респондент (экспериментальный случай) был инструктирован выполнять тест в хаотичном, бессистемном режиме, игнорируя инструкцию к тесту.

У каждого респондента было сделано 85 замеров времени реакции, с тем чтобы можно было делать подвыборки измерений следующих размеров (n): 10, 20, 30, 40, 50, 60 и 70 с 105 репликациями для каждого объёма выборки. Данные случайным образом выбирались из всего массива измерений без возвращения. Предварительно данные о времени реакции были стандартизированы и возведены в 10-ю степень, то есть

γ = 10

.

Для проверки функциональности установленных критических значений статистик

m^{}

и

d^{}

проведён статистический анализ методом расчёта показателя отношения шансов. Исследовалось, влияет ли поведение респондента при прохождении теста Струпа на вероятность отвергнуть нулевую гипотезу о соответствии распределения первой значащей цифры времени реакции закону Бенфорда при

α = 0,05

, используя установленные критические значения на основе данных симуляций. Такой уровень значимости объясняется тем, что он является конвенциональным в психологической науке [Dixon, 2003]. Сначала рассчитывался простой показатель шанса (odds, O) отвергнуть нулевую гипотезу для контрольного и экспериментального случая:

\begin{matrix} O = \frac{p_{1}}{p_{0}}, \end{matrix}

где

p_{1}

– вероятность отвергнуть нулевую гипотезу,

p_{0}

– обратное событие (

{1 - p}_{1}

).

Затем шанс экспериментального условия делился на шанс контрольного, тем самым получалось отношение шансов (odds ratio, OR):

\begin{matrix} = \frac{O_{э}}{O_{к}} \end{matrix}

Для интерпретации отношения шансов использованы данные исследования Чена и коллег [Chen, 2010]. Согласно их исследованию, малый эффект наблюдается при отношении шансов, находящемся в полуинтервале [1,52; 2,74), средний – в полуинтервале [2,74; 4,72), большой – в полуинтервале [4,72; +∞).

Симуляция данных выполнена в среде R [R Core Team, 2021] с использованием базовых функций «rlnorm» и «sample». Статистическая обработка данных проходила в программе jamovi [The jamovi project, 2023]. Визуализация выполнена с помощью Microsoft® Excel [Microsoft Corporation. Microsoft, 2018].

Результаты

Симуляционное исследование

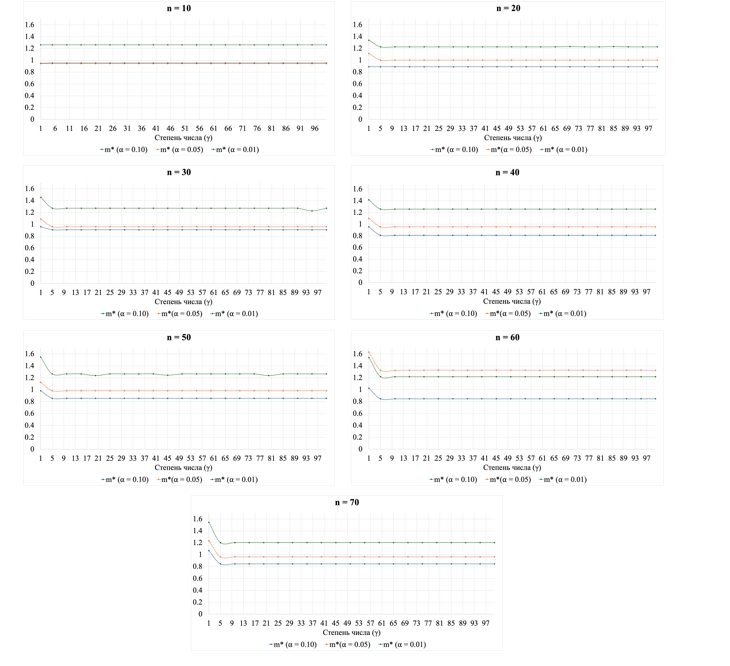
На рисунке 2 представлено поведение статистики

m^{}

в зависимости от объёма выборки и степени числа. Можно заметить, что критические значения отличаются в зависимости от объёма выборки, это подтверждает дисперсионный анализ: F(6, 140) = 45,709, p < 0,001. При этом также можно наблюдать, что значения статистики стабилизируются при

γ \geq 5

, что даёт возможность предположить, что её значения не зависят от степени числа.

Рис. 2. Поведение статистики

m^{}

в зависимости от объёма выборки и степени числа в симуляционном исследовании.

В таблице 1 представлены корреляции Спирмена для разных объёмов выборки между степенью числа и значением статистики

m^{}

с учётом исключения выбросов. Как правило, выбросы наблюдаются при

γ = 1

. Отметим, что корреляции не являются значимыми, следовательно, можно заключить, что связи между степенью числа и значением статистики

m^{}

нет. Причём связь отсутствует вне зависимости от объёма выборки.

Таблица 1. Корреляции Спирмена для разных объёмов выборки между степенью числа и значением статистики $m^{}$ с учётом исключения выбросов

Объём выборки (n)	$m^{} (α = 0,10)$	$m^{} (α = 0,05)$	$m^{} (α = 0,01)$
10	0,00	0,00	0,00
20	0,00	0,00	0,29
30	0,00	0,00	-0,34
40	0,00	0,00	0,00
50	0,00	0,00	0,06
60	0,00	0,00	0,00
70	0,00	0,00	0,00

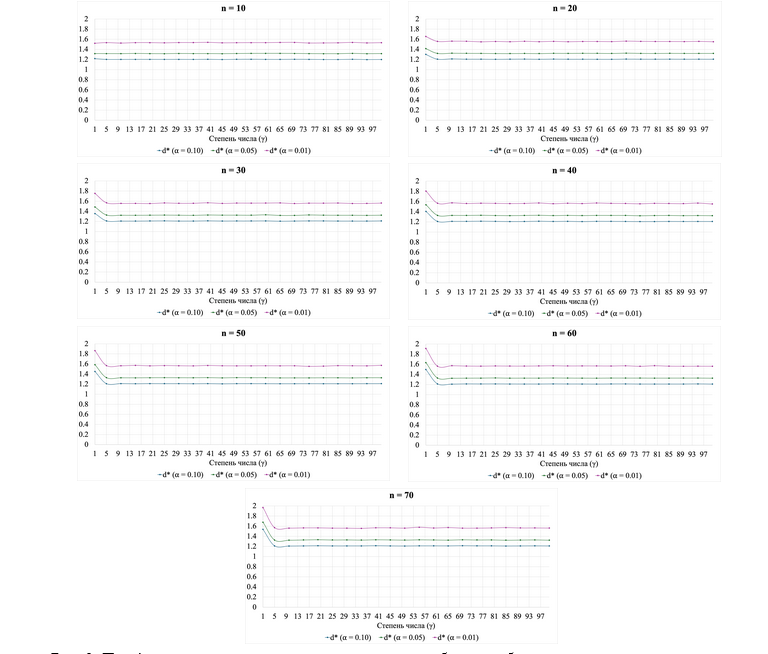
На рисунке 3 представлено поведение статистики

d^{}

в зависимости от объёма выборки и степени числа. Как и в случае со статистикой

m^{}

, критические значения

d^{}

отличаются в зависимости от объёма выборки, это подтверждает дисперсионный анализ: F(6, 140) = 34,755, p < 0,001. При этом также можно наблюдать, что значения статистики стабилизируются при

γ \geq 5

, что даёт возможность предположить, что её значения не зависят от степени числа.

Рис. 3. Поведение статистики

d^{}

в зависимости от объёма выборки и степени числа в симуляционном исследовании.

В таблице 2 представлены корреляции Спирмена для разных объёмов выборки между степенью числа и значением статистики

d^{}

с учётом исключения выбросов. Как правило, выбросы наблюдаются при

γ = 1

. Отметим, что корреляции не являются значимыми, однако наблюдается большая зависимость от степени числа, чем у статистики

m^{}

.

Таблица 2. Корреляции Спирмена для разных объёмов выборки между степенью числа и значением статистики $d^{}$ с учётом исключения выбросов

Объём выборки (n)	$d^{} (α = 0,10)$	$d^{} (α = 0,05)$	$d^{} (α = 0,01)$
10	-0,17	0,03	-0,08
20	-0,20	0,01	-0,23
30	-0,01	-0,18	-0,06
40	-0,37	-0,55*	-0,38
50	-0,11	-0,33	-0,24
60	-0,40	0,01	-0,29
70	0,05	-0,15	0,04
Прим. * p < 0,05

В таблице 3 представлены критические значения для статистики

m^{}

, полученные в рамках симуляционного исследования. Отдельно указаны асимптотические значения статистики, полученные в исследовании Джона Морроу [Morrow, 2014]. Можно заметить, что симуляционные и асимптотические критические значения становятся близки при увеличении объёма выборки.

Таблица 3. Критические значения для $m^{}$ при разных уровнях значимости

Объём выборки	$α = 0,10$	$α = 0,05$	$α = 0,01$
10	0,946	0,958	1,262
20	0,890	1,002	1,225
30	0,907	0,958	1,273
40	0,809	0,955	1,259
50	0,856	0,983	1,266
60	0,847	0,968	1,219
70	0,845	0,965	1,204
Дж. Морроу (n > 80)	0,851	0,967	1,212

В таблице 4 представлены критические значения для статистики

d^{}

, полученные в рамках симуляционного исследования. Отдельно указаны асимптотические значения статистики, полученные в исследовании Джона Морроу [Morrow, 2014]. В отличие от

m^{}

, симуляционные критические значения

d^{}

достаточно близки к асимптотическим при любом значении

α

.

Таблица 4. Критические значения для $d^{}$ при разных уровнях значимости

Объём выборки	$α = 0,10$	$α = 0,05$	$α = 0,01$
10	1,204	1,321	1,538
20	1,208	1,326	1,563
30	1,211	1,331	1,569
40	1,213	1,330	1,574
50	1,211	1,329	1,572
60	1,212	1,330	1,571
70	1,214	1,333	1,578
Дж. Морроу (n > 80)	1,212	1,330	1,569

По итогам симуляционного исследования можно заключить, что, по нашим данным, статистика

m^{}

в сравнении с

d^{}

более предпочтительна при изучении соответствия распределения первой значащей цифры стандартизированного значения времени реакции закону Бенфорда, поскольку она не зависит от степени, в которую возводят стандартизированное значение (в пределах

5 \leq γ \leq 100

).

Экспериментальное исследование

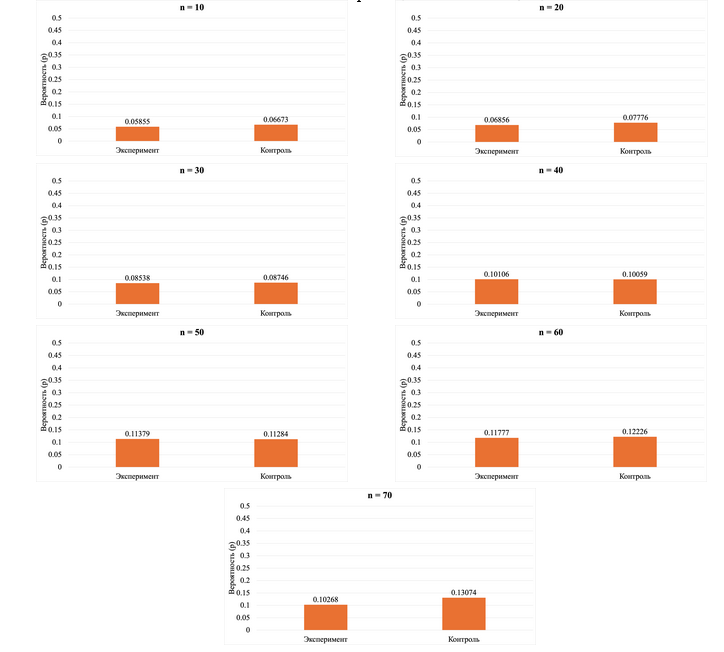
На рисунке 4 представлены вероятности отвержения нулевой гипотезы о соответствии распределения первой значащей цифры закону Бенфорда для экспериментального и контрольного случаев в разрезе разных объёмов выборки. Можно заметить, что распределение вероятности для контрольного случая флуктуирует в районе значения 0,06, при этом для экспериментального увеличивается при увеличении объёма выборки. Также на основе представленных вероятностей можно рассчитать отношение шансов при сравнении экспериментального и контрольного случаев.

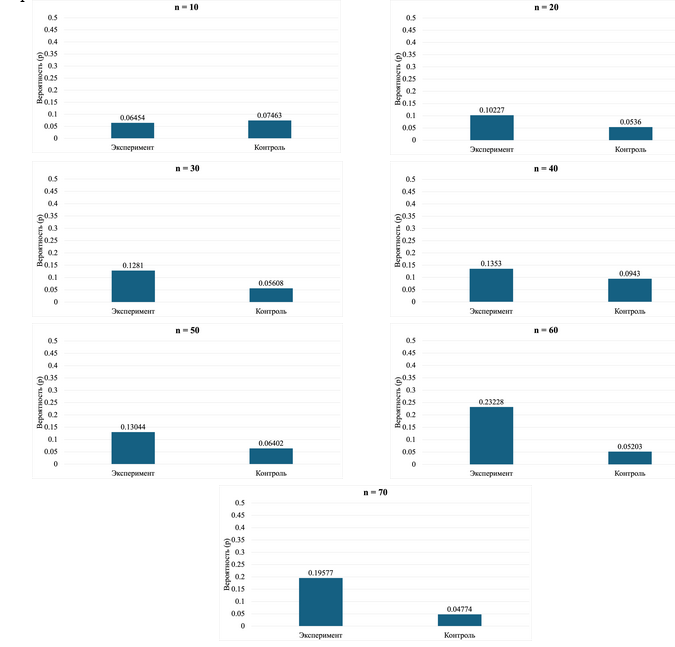
Рис. 4. Вероятность отвержения нулевой гипотезы о соответствии распределения первой значащей цифры закону Бенфорда для экспериментального и контрольного случаев на основе статистики

m^{}

.

При n = 10 шанс отвергнуть нулевую гипотезу в экспериментальном случае равен

\frac{0,06454}{1 - 0,06454} = 0,068992795

, в контрольном –

\frac{0,07463}{1 - 0,07463} = 0,080648822

. При этом отношение шансов (эксперимент vs. контроль) составляет

\frac{0,068992795}{0,080648822} = 0,85547183 \approx 14 %

. То есть в экспериментальном случае шанс отвергнуть нулевую гипотезу примерно на 14% ниже, чем в контрольном. Или, если перевернуть отношение шансов, то получится, что в контрольном случае на 17% выше шанс отвергнуть нулевую гипотезу, чем в экспериментальном:

\frac{0,080648822}{0,068992795} = 1,168945563 \approx 17 %

. При n = 20 шанс отвергнуть нулевую гипотезу в экспериментальном случае равен

\frac{0,10227}{1 - 0,10227} = 0,113920667

, в контрольном –

\frac{0,0536}{1 - 0,0536} = 0,056635672

. При этом отношение шансов (эксперимент vs. контроль) составляет

\frac{0,113920667}{0,056635672} = 2,011464904 \approx 101 %

. То есть в экспериментальном случае шанс отвергнуть нулевую гипотезу примерно в 2 раза (или на 101%) выше, чем в контрольном. При n = 30 шанс отвергнуть нулевую гипотезу в экспериментальном случае равен

\frac{0,1281}{1 - 0,1281} = 0,146920518

, в контрольном –

\frac{0,05608}{1 - 0,05608} = 0,059411815

. При этом отношение шансов (эксперимент vs. контроль) составляет

\frac{0,146920518}{0,059411815} = 2,472917542 \approx 147 %

. То есть в экспериментальном случае шанс отвергнуть нулевую гипотезу почти в 2.5 раза (или на 147%) выше, чем в контрольном. При n = 40 шанс отвергнуть нулевую гипотезу в экспериментальном случае равен

\frac{0,1353}{1 - 0,1353} = 0,156470452

, в контрольном –

\frac{0,0943}{1 - 0,0943} = 0,104118361

. При этом отношение шансов (эксперимент vs. контроль) составляет

\frac{0,156470452}{0,104118361} = 1,50281324 \approx 50 %

. То есть в экспериментальном случае шанс отвергнуть нулевую гипотезу в 1.5 раза (или на 50%) выше, чем в контрольном. При n = 50 шанс отвергнуть нулевую гипотезу в экспериментальном случае равен

\frac{0,13044}{1 - 0,13044} = 0,1500069

, в контрольном –

\frac{0,06402}{1 - 0,06402} = 0,068398897

. При этом отношение шансов (эксперимент vs. контроль) составляет

\frac{0,1500069}{0,068398897} = 2,193118686 \approx 119 %

. То есть в экспериментальном случае шанс отвергнуть нулевую гипотезу почти в 2.2 раза (или на 119%) выше, чем в контрольном. При n = 60 шанс отвергнуть нулевую гипотезу в экспериментальном случае равен

\frac{0,23228}{1 - 0,23228} = 0,302558224

, в контрольном –

\frac{0,05203}{1 - 0,05203} = 0,054885703

. При этом отношение шансов (эксперимент vs. контроль) составляет

\frac{0,302558224}{0,054885703} = 5,512514318 \approx 451 %

. То есть в экспериментальном случае шанс отвергнуть нулевую гипотезу в 5.5 раза (или на 451%) выше, чем в контрольном. При n = 70 шанс отвергнуть нулевую гипотезу в экспериментальном случае равен

\frac{0,19577}{1 - 0,19577} = 0,243425388

, в контрольном –

\frac{0,04774}{1 - 0,04774} = 0,050133367

. При этом отношение шансов (эксперимент vs. контроль) составляет

\frac{0,243425388}{0,050133367} = 4,855556352 \approx 386 %

. То есть в экспериментальном случае шанс отвергнуть нулевую гипотезу почти в 4.9 раза (или на 386%) выше, чем в контрольном.

На основе границ размеров эффекта можно сделать вывод, что при объёме выборки от 10 до 50 различия между экспериментальным и контрольным случаем довольно малы. В то же время при n = 60 и n = 70 различия являются большими.

На рисунке 5 представлены вероятности отвержения нулевой гипотезы о соответствии распределения первой значащей цифры закону Бенфорда на основе статистики

d^{}

для экспериментального и контрольного случаев в разрезе разных объёмов выборки. Можно заметить, что распределение вероятности обоих случаев нестабильно, изменяется в зависимости от объёма выборки – увеличивается при увеличении n.

Рис. 5. Вероятность отвержения нулевой гипотезы о соответствии распределения первой значащей цифры закону Бенфорда для экспериментального и контрольного случаев на основе статистики

d^{}

.

При n = 10 шанс отвергнуть нулевую гипотезу в экспериментальном случае равен

\frac{0,05855}{1 - 0,05855} = 0,062191301

, в контрольном –

\frac{0,06673}{1 - 0,06673} = 0,07150128

. При этом отношение шансов (эксперимент vs. контроль) составляет

\frac{0,062191301}{0,07150128} = 0,869792824 \approx 13 %

. То есть в экспериментальном случае шанс отвергнуть нулевую гипотезу примерно на 13% ниже, чем в контрольном. При n = 20 шанс отвергнуть нулевую гипотезу в экспериментальном случае равен

\frac{0,06856}{1 - 0,06856} = 0,073606459

, в контрольном –

\frac{0,07776}{1 - 0,07776} = 0,084316447

. При этом отношение шансов (эксперимент vs. контроль) составляет

\frac{0,073606459}{0,084316447} = 0,87297866 \approx 13 %

. То есть в экспериментальном случае шанс отвергнуть нулевую гипотезу примерно на 13% ниже, чем в контрольном. При n = 30 шанс отвергнуть нулевую гипотезу в экспериментальном случае равен

\frac{0,08538}{1 - 0,08538} = 0,093350244

, в контрольном –

\frac{0,08746}{1 - 0,08746} = 0,095842374

. При этом отношение шансов (эксперимент vs. контроль) составляет

\frac{0,093350244}{0,095842374} = 0,973997616 \approx 3 %

. То есть в экспериментальном случае шанс отвергнуть нулевую гипотезу на 3% ниже, чем в контрольном. При n = 40 шанс отвергнуть нулевую гипотезу в экспериментальном случае равен

\frac{0,10106}{1 - 0,10106} = 0,112421296

, в контрольном –

\frac{0,10059}{1 - 0,10059} = 0,111839984

. При этом отношение шансов (эксперимент vs. контроль) составляет

\frac{0,112421296}{0,111839984} = 1,005197714 \approx 0,5 %

. То есть в экспериментальном случае шанс отвергнуть нулевую гипотезу в 1,005 раза (или на 0,5%) выше, чем в контрольном. При n = 50 шанс отвергнуть нулевую гипотезу в экспериментальном случае равен

\frac{0.11379}{1 - 0.11379} = 0.128400718

, в контрольном –

\frac{0,11284}{1 - 0,11284} = 0,127192389

. При этом отношение шансов (эксперимент vs. контроль) составляет

\frac{0,128400718}{0,127192389} = 1,009500006 \approx 1 %

. То есть в экспериментальном случае шанс отвергнуть нулевую гипотезу почти в 1,01 раза (или на 1%) выше, чем в контрольном. При n = 60 шанс отвергнуть нулевую гипотезу в экспериментальном случае равен

\frac{0,11777}{1 - 0,11777} = 0,133491266

, в контрольном –

\frac{0,12226}{1 - 0,12226} = 0,139289539

. При этом отношение шансов (эксперимент vs. контроль) составляет

\frac{0.133491266}{0.139289539} = 0.958372519 \approx 4 %

. То есть в экспериментальном случае шанс отвергнуть нулевую гипотезу на 4% ниже, чем в контрольном. При n = 70 шанс отвергнуть нулевую гипотезу в экспериментальном случае равен

\frac{0,10268}{1 - 0,10268} = 0,114429635

, в контрольном –

\frac{0,13074}{1 - 0,13074} = 0,150403792

. При этом отношение шансов (эксперимент vs. контроль) составляет

\frac{0,114429635}{0,150403792} = 0,760816158 \approx 24 %

. То есть в экспериментальном случае шанс отвергнуть нулевую гипотезу почти на 24%) ниже, чем в контрольном.

В случае с использованием статистики

d^{}

получается парадоксальная ситуация – шансы отвергнуть нулевую гипотезу оказываются немного выше в контрольном случае, нежели в экспериментальном. Правда шансы достаточно малы по размеру, это означает, что они практически не отличаются в обоих случаях.

Заключение

В предлагаемом исследовании на основе симуляций из лог-нормального распределения, отражающего распределение времени реакции, с параметрами μ= 5.984, σ= 0.1245 изучалось поведение статистик согласия

m^{}

и

d^{}

. Выяснилось, что значения

m^{}

не зависят от степени, в которую возводят стандартизированное значение времени реакции, в то время как у

d^{}

наблюдается небольшая отрицательная зависимость. Обе статистики зависят от объёма выборки (n), поэтому для каждого из анализируемых n были установлены отдельные критические значения при

α = 0,10

,

α = 0,05

и

α = 0,01

.

Необходимо отметить, что результаты наших симуляций относительно статистики

d^{}

совпадают с заключениями Л. Кампанелли [Campanelli, 2024], который вывел линейные закономерности между n и

d^{}

. Так, для

26 \leq n \leq 1000

зависимость выглядит следующим образом:

\begin{matrix} d_{N,1 - α}^{} = a + b n^{- 1} \end{matrix}

К примеру, при

α = 0,05

для

50 \leq n \leq 1000

коэффициенты его формулы принимают вид:

a = 1,3286, b = - 0,1151

. Если подставить n=50, то получится 1,326. В нашем случае критическое значение равняется 1,329, что довольно близко к результату по формуле Кампанелли (естественно, в рамках погрешности метода). По такой же логике можно проверить остальные критические значения. При этом важно учесть, что при

26 \leq n \leq 49

коэффициенты

a

и

b

другие, а для

5 \leq n \leq 25

значения представлены в табличном виде. Однако несмотря на сходство полученных результатов, статистика

d^{}

оказалась нефункциональна при сравнении данных экспериментального исследования. Она оказалась нечувствительна к изменениям в поведении испытуемых, что отразилось в практически одинаковых шансах отвергнуть нулевую гипотезу о соответствии распределения первой значащей цифры закону Бенфорда.

Если говорить о статистике

m^{}

, то как уже было отмечено, она оказалась менее чувствительной к степени, в которую мы возводили стандартизированное значение времени реакции, чем

d^{}

. Кроме того, она оказалась более функциональной при сравнении двух разных паттернов поведения в экспериментальном исследовании. Выяснилось, что в эмпирическом исследовании при

20 \leq n \leq 70

в экспериментальном случае шансы отвергнуть нулевую гипотезу о соответствии распределения первой значащей цифры стандартизированного значения времени реакции закону Бенфорда выше, чем в контрольном. Причём при

60 \leq n \leq 70

эти шансы в 4–5 раз выше. Это даёт нам основание предположить, что статистика

m^{}

позволяет лучше дифференцировать достоверные и недостоверные данные при измерении времени реакции. Тем не менее, требуются другие исследования (например, с симуляциями из отличных от лог-нормального распределений), чтобы увереннее говорить о большей полезности статистики

m^{}

в сравнении с

d^{}

при анализе данных о времени реакции.

Ограничения исследования

Предлагаемое исследование имеет ряд ограничений. Во-первых, в части симуляций был сделан упор на лог-нормальное распределение с конкретными параметрами. В связи с этим полученные закономерности неправомерно распространять на другие виды распределений или даже на лог-нормальное с иными значениями

μ

и

σ

. Требуются дальнейшие исследования по изучению свойств

m^{}

и

d^{}

. Во-вторых, функциональность статистик

m^{}

и

d^{}

изучалась в рамках эксперимента всего с двумя испытуемыми, что ограничивает возможности обобщения выводов на более широкие случаи. Более того, экспериментальные условия и методика измерений были настроены под специфику дизайна и идеи исследования, что может влиять на воспроизводимость результатов в иных контекстах. Следовательно, крайне важно продолжить исследовательскую работу, направленную на проверку полученных результатов в более разнообразных условиях и с использованием различных методологических подходов, что позволит укрепить достоверность выводов и их применимость в более широком спектре ситуаций.

Применение статистик m* и d* для оценки качества данных психологического исследования с помощью закона Бенфорда (на примере измерения времени реакции)

Резюме

Общая информация

Полный текст

Введение

Время реакции

Закон Бенфорда

Модификации статистических тестов согласия с законом Бенфорда

Результаты

Экспериментальное исследование

Заключение

Ограничения исследования

Литература

Информация об авторах

Метрики

Просмотров web

Скачиваний PDF

Всего