1. ВВЕДЕНИЕ
Многие математики и философы науки уверены, что математические объекты в той или иной форме существует реально. Это мнение очень ярко было выражено Шарлем Эрмитом: «Я верю, что числа и функции анализа не являются произвольным созданием нашего разума; я думаю, что они существуют вне нас в силу той же необходимости, как и объекты реального мира, и мы их ворочаем или открываем и изучаем точно так же, как это делают физики, химики или зоологи» [Клайн, 1984].
Для математика, работающего в области прикладной математики, такой взгляд на математические объекты представляется в высшей степени естественным. Для него на первый план выходят не доказательства (хотя и они отчасти сохраняют своё значение), а деятельность иного рода. Поскольку важнейшим структурным элементом любой деятельности является целеполагание, разделение математики на чистую и прикладную может быть проведено именно по этому признаку. Математика может рассматриваться либо как цель научного исследования (чистая математика), либо как средство для достижения внематематических целей (прикладная математика) [Блехман, 1983].
Поскольку число областей, к которым прилагается математика, чрезвычайно велико, столь же многочисленны по форме и методы математиков-прикладников. Из всего этого многообразия выделим только приёмы работы, сходные по характеру с конструированием. Часто именно так происходит получение новых результатов в сфере компьютерной геометрии. В тех случаях, когда оно направленно на разработку эффективных методов построения компьютерных изображений, функции используются, как конструктивные элементы этих изображений. В частности иногда их графики объединяются, как своеобразные твёрдые фигурные стержни, для получения гладкой кривой, которая обладает теми или иными свойствами. Подобный способ интеллектуальной работы можно было бы назвать предметно-образным манипулированием математическими объектами. Компьютерный геометр, используя образы линий, «ворочает» кривые подобно предметам и составляет из них изображения.
Один из широко известных методов гладкого сопряжения кривых основан на использовании сплайнов. Гладкая кривая, проходящая через заданные точки плоскости и в каждой из них имеющая заданное направление, конструируется как график кусочно-многочленной функции, состоящей из графиков многочленов третьей степени. Этот подход имеет значительные преимущества перед классическим аппаратом построения интерполяционных многочленов [Завьялов, 1980]. Рассматриваемый в данной статье метод также предполагает составление гладких кривых из отдельных кусков, гладко сопрягаемых между собой.
Ещё одним активно используемым способом построения гладких кривых является метод Пьера Безье. Изначально его идея была основана на геометрических и кинематических соображениях и лишь в дальнейшем получила алгебраическое истолкование, связанное с многочленами Бернштейна [Роджерс, 2001]. Предлагаемый нами метод также основывается на идеях геометрического и кинематического характера, но может быть истолкован и аналитически.
Метод криволинейных координат, к описанию которого мы приступаем, основан на соображениях, изложенных автором в статье [Степанов, 2011]. Вкратце их суть такова.
-
Многие геометрические объекты естественным образом истолковываются как траектории движущихся точек или линий. Это связано с тем, что кинематика «является геометрией движущихся материальных объектов» [Берёзкин, 1974]. Именно по этой причине использование механического движения есть важнейший путь к пониманию внутренних закономерностей формы объекта.
-
Для анализа формы геометрического объекта может быть использован метод сложных движений, приводящий к разработке алгоритма построения изображения. Этот метод позволяет строить цепочку математических вычислений, отталкиваясь от последовательности порождающих объект простых движений.
-
Для разработки алгоритма первоначально проводится анализ формы объекта, направленный на поиск сложного движения, приводящего к построению объекта как некоторой траектории. Кроме того, соответствующее сложное движение разлагается в совокупность простых движений.
-
Каждое простое движение является движением пространственно-подобного элемента (плоскости, прямой, точки) в пространстве большей размерности.
-
Движение каждого такого элемента описывается аффинным или евклидовым преобразованием.
-
Алгоритм возникает как цепочка последовательных вычислений координат движущихся точек. Соответствующие координаты изменяются в результате простых движений, а в совокупности эти простые движения создают целостное сложное движение.
-
Перейдём к описанию метода криволинейных координат.
2. КИНЕМАТИЧЕСКАЯ ИНТЕРПРЕТАЦИЯ ПОСТРОЕНИЯ КРИВЫХ В ДЕКАРТОВЫХ КООРДИНАТАХ
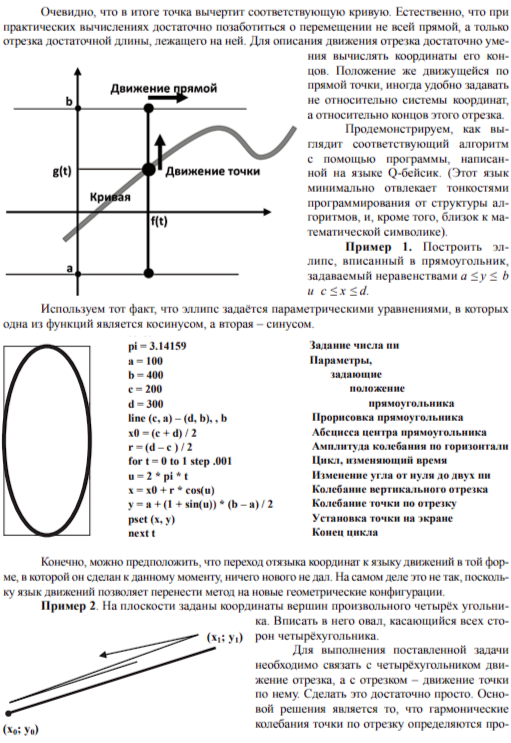
Пусть на плоскости задана декартова система координат. Рассмотрим плоскую кривую, которая описывается с помощью двух параметрических уравнений х = f(t) и у = g(t). Будем считать параметр t временем. Тогда построение кривой можно провести, соединив в одно сложное движение следующие простые движения.
-
Перемещение по плоскости прямой, всегда остающейся параллельной оси ординат, так, что абсциссы всех точек, лежащих на ней, в момент времени t равны f(t).
-
Перемещение по упомянутой прямой точки так, что её ордината в момент времени t равна g(t).




3. ПРИМЕНЕНИЕ КИНЕМАТИЧЕСКОГО МЕТОДА ДЛЯ ПОСТРОЕНИЯ ИЗОБРАЖЕНИЙ

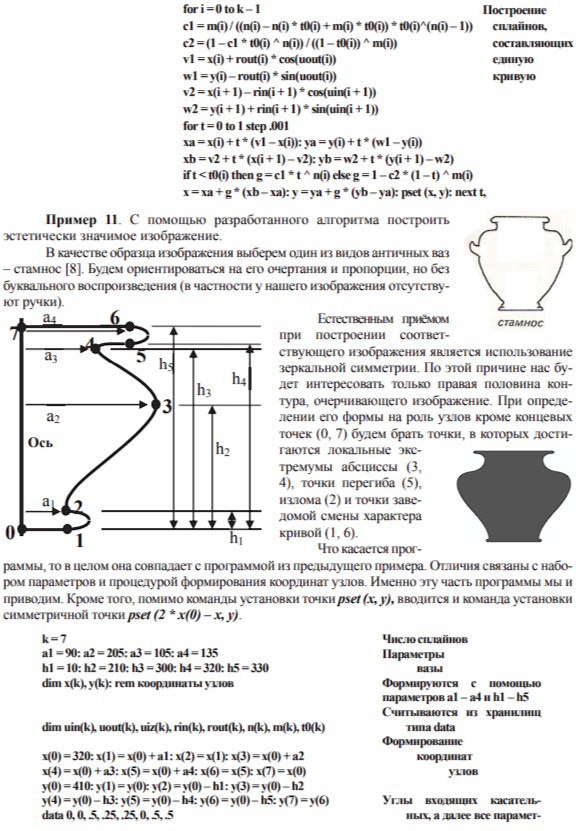
Отметим, что меняя параметры а1 - а4 и h1 - h5, можно варьировать форму вазы весьма значительно. Это обстоятельство приводит нас к важному вопросу, который требует специального рассмотрения. Здесь же мы только затронем его.
Речь идёт о методах математического описания формы. «Есть ярко выраженная потребность в строго разработанной науке морфологии, которая бы занималась принципами, лежащими в основе описания форм. Математика описания форм, как возможная область исследования, до настоящего времени строго не развивалась, или даже не была признана в достаточной степени» [Лорд, 2003]. Несомненно, для компьютерной геометрии этот вопрос является центральным.
В дальнейшем мы ограничимся тем, что на основе приёма, использованного в предыдущем примере, сформулируем эмпирическое правило описания формы плоских кривых. Однако сначала нами будут изложены некоторые соображения общего характера, позволяющие оценить значение затронутой проблемы. При этом мы обратимся к некоторым понятиям и идеям искусствоведения и биологии.
Во многих культурах при создании изображений художественного и религиозного характера используется канон. Канон - «совокупность твёрдо установленных правил, определяющих в художественном произведении нормы композиции и колорита, систему пропорций, либо иконографию данного типа изображения» [Большая Советская Энциклопедия]. Для ряда стран и эпох, характеризующихся высоким уровнем развития изобразительного искусства, типично стремление осмыслить сущность канона и обосновать его с помощью тех или иных математических принципов. «Для античности и Возрождения характерны попытки рационалистическим путём найти идеальную закономерность в пропорциях человеческого тела и вывести неизменные, математически обоснованные правила построения человеческой фигуры» [Большая Советская Энциклопедия].
Несомненно, что истоком этой тенденции стало древнеегипетское искусство. «Подобно тому, как сущность философской концепции определяется тем, что принимается ею за первооснову, так же и канон как специфическая форма художественного мышления должен был иметь свою первооснову, которая бы организовывала и уравновешивала все составляющие его компоненты. И здесь в качестве формообразующей структуры канона выступает система пропорциональных соотношений» [Померанцева, 1985].
Кроме понятия канона мы затронем ещё и одно понятие - архетип (от греческих arche - начало и typos - образ) [Большой Энциклопедический Словарь]. Термин «архетип» может быть успешно заменён русским словом «прообраз». В биологии архетип - это «представление о первичном типе, прототипе, строения скелета всех позвоночных животных, выдвинутое Р. Оуэном (1847). Теория архетипов основывается на сопоставлении общих признаков, свойственных скелету различных позвоночных, и создаёт отвлечённый образ, идеальный тип скелета, не реализованный полностью ни в одном из вымерших или ныне живущих животных... Дарвин переосмыслил понятие архетипа, представлял его не как абстрактный прототип, а как реально существовавшую некогда прародительскую форму» [Большая Советская Энциклопедия].
При описании морфологии плоских кривых мы будем отталкиваться от понятий архетипа, канона и пропорции, толкуя их весьма свободно. Мы решаем задачу построения кривой, обладающей определёнными свойствами. (Более правильно было бы говорить о построении целого класса кривых, одновременно имеющих и узнаваемую форму, и обладающих индивидуальными чертами).
Роль архетипа кривой будут играть либо набор узлов, заданный непосредственно, либо некоторая конкретная кривая, с выделенными на ней узлами. Обычно мы будем задавать кривую-архетип параметрически.
Переход от архетипа к канону, то есть к подвижной кривой, обретающей нужную форму и, тем самым, наполняющейся смыслом, осуществляется с помощью векторов смещающих узлы в новое положение. Наконец, роль пропорций играют параметры кривой одного росчерка (углы наклона входящей и исходящей касательных, длины входящей и исходящей стороны четырёхугольника, а также параметры сплайна сопрягающего данный узел со следующим).
Если обратиться к построению вазы, роль архетипа играет вертикальный отрезок, относительно которого указаны смещения узлов канона. Канон определяет очертания вазы. Но конкретную форму ваза приобретает только после выбора соответствующих пропорций.
Отметим, что предлагаемый подход имеет связь с ещё одной биологической теорией. «В последней главе своего фундаментального труда «О росте и форме» д’Арси Томпсон выдвинул гипотезу, которую он рассматривает как идею общего аналитического подхода к изучению формы у близкородственных видов. Эта гипотеза формулируется весьма просто и в основном сводится к следующему: если принять форму какого-то данного организма за эталон и отнести эту форму к некоторой декартовой прямоугольной системе координат, то форму всякого, организма, достаточно близкого к начальному, можно рассматривать как результат непрерывной деформации исходной координатной системы» [Розен, 1969].
Предлагаемый нами подход как раз и направлен не на построение одной, пусть и обладающей исключительными свойствами, кривой. Речь идёт о создании некого «морфологического пространства», определяемого набором многочисленных, но геометрически обусловленных параметров. Их изменение обеспечивает возможность целенаправленной непрерывной деформации исходного изображения.
Именно с этим обстоятельством связано введение варианта, при котором архетип задаётся в виде кривой. Ведь непосредственное задание узлов, казалось бы, даёт тот же результат без лишних вычислений. Однако кривая может послужить более удобным средством построения и использования деформаций для получения новых форм. К этому вопросу мы обратимся позднее.
Окончательно сформулируем правила построения плоских кривых, обладающих определёнными морфологическими свойствами.
-
Выбирается архетип, представляющий собой либо набор узлов, указанных непосредственно, либо кривую, заданную параметрически. В последнем случае на кривой-архетипе фиксируются базовые точки. Отметим, что универсальным средством параметрического задания кривых являются ряды Фурье.
-
С каждой базовой точкой связывают вектор, задающий её перемещение в узел, который будет лежать на кривой, которую мы строим.
-
Для каждого узла задаются углы наклона входящей и исходящей касательных. Обычно эти углы одинаковы при поиске кривых, имеющих сходную морфологию и наиболее приемлемых с точки зрения поставленной задачи.
-
Для окончательного построения конкретной кривой задаются остальные параметры, то есть длины входящей и исходящей стороны четырёхугольника и параметры сплайнов, сопрягающих соседние узлы. Именно их подбор приводит к построению кривой, принимающей окончательный индивидуальный облик.



Конечно, попытка прорисовки человеческого профиля является достаточно рискованным предприятием. Дело в том, что здесь затрагиваются тонкие эстетические ощущения. На самом деле и в технике дело обстоит аналогичным образом. «От формы изделия зависит его эстетическое восприятие» [Завьялов, 1985]. Поэтому при современном состоянии возможностей компьютерной графики необходимо рисковать.
К тому же совершенно ясно, что подбор параметров, осуществляемый вручную, весьма неудобен. Но на основе описанного алгоритма можно написать программу, позволяющую осуществлять выбор архетипа, смещений и параметров сплайнов в интерактивном режиме. Подобная программа может использоваться как удобный инструмент художника или дизайнера. Однако этот круг вопросов мы в данной статье не рассматриваем.
4. ПОСТРОЕНИЕ ЛИНИЙ В КРИВОЛИНЕЙНЫХ КООРДИНАТАХ
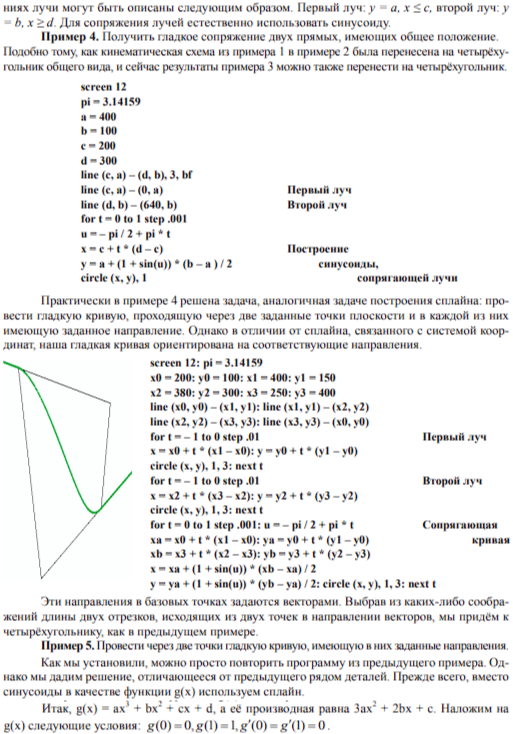
Перейдём к аналитической интерпретации предложенного выше кинематического метода. Для этого ещё раз объясним, как точка с декартовыми координатами (t1; t2) переносится на плоскость, связанную с четырёхугольником (сохраняются обозначения примера 2).
Основой отображения является соответствие вершин единичного квадрата (0; 0), (1; 0), (1; 1), (0; 1) вершинам четырёхугольника (х0; у0), (х1; у1), (х2; у2), (х3; у3) соответственно. Координаты двух точек A(t1; 0) и B(t1; 1), определяющих в декартовой системе координат вертикальную прямую, переходят в точки P и Q:
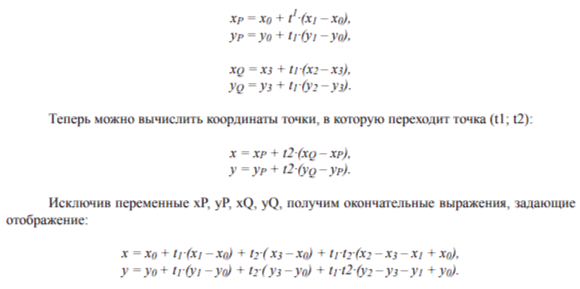
Поскольку переменные х и у выражаются через переменные t1 и t2 нелинейно, мы имеем дело с криволинейной системой координат.
Вообще говоря, криволинейная система координат представляет собой отображение прямоугольной системы координат (ti; t2) в систему координат (х; у) с помощью аналитических функций X = X(t1, t2) и у = y(t1, t2). Изменяя ti при постоянных значениях t2 (и наоборот, изменяя t2 при постоянных значениях t1) можно вычертить координатные линии криволинейной системы координат [Математический энциклопедический словарь, 1988].
Поскольку отображение осуществляется с помощью гладких функций, отображение переводит кривые, которые касались друг друга в прямоугольной системе координат, в соприкасающиеся кривые в криволинейной системе координат. Именно это обстоятельство и является важнейшим для предлагаемого нами метода.
Следует особо отметить, что важное с теоретической точки зрение требование взаимной однозначности отображения при практическом применении метода криволинейных координат иногда может быть опущено (примеры 2 и 6).
Пока мы использовали только весьма частный вид криволинейных систем координат. Однако при перенесении метода на системы координат общего вида никаких затруднений возникнуть не может. Тем не менее, прежде чем приводить примеры, дадим словесное описание алгоритма.
-
Пусть задана криволинейная система координат, заданная с помощью функций х = x(t1, t2) и у =y(ti, t2). Ставится задача гладкого сопряжения двух кривых х = x(t1, 0) и у = y(ti, 1), являющихся координатными линиями данной криволинейной системы координат.
-
Для более точной постановки задачи на соответствующих кривых необходимо указать точки, через которые проходит сопрягающая кривая, например, точки, определяемые параметрами t1 =0, t2 = 0 и ti =1, t2 = 1.
-
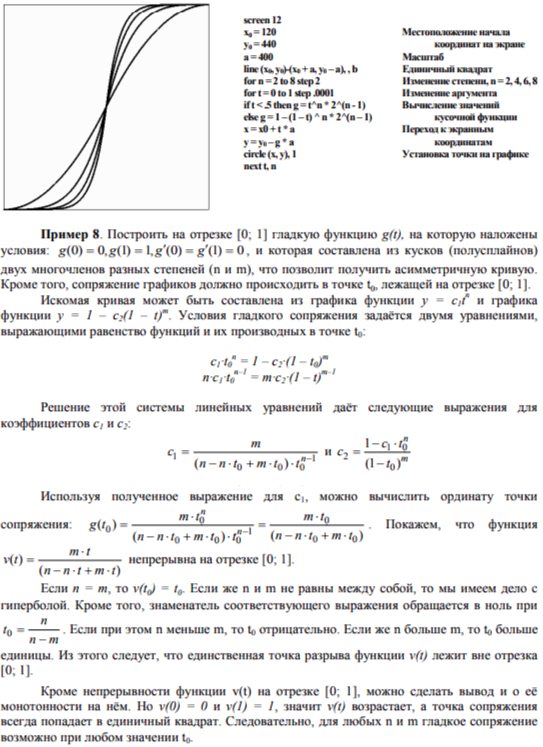
Сопряжение осуществляется графиком функции t2 = g(t1), на которую наложен условия: g(0) = 0,g(1) = 1,g'(0) = g'(1) = 0 . График строится в криволинейны координатах н отрезке [0; Клайн, 1984].
-
Переход к сопряжению произвольных координатных линий в произвольной точке может быть произведено с помощью введения новой параметризации. Например, если точка сопряжения (а, значит, и координатные линии) определяются параметрами ti =a, t2 = c и ti =b , t2 = d, можно ввести новые параметры р i и р2, помощью формул t1 = a + p1(b - a) и t2 = c + p(d - c). где р1 и р2 меняются



Построенное нами изображение можно рассматривать как некий курьёз, однако, это не так. Кратко аргументируем это утверждение. Прежде всего, отметим, что с момента возникновения геометрии Лобачевского - первой неевклидовой геометрии, возникла и идея неевклидовой механики. Уже в 1829 Лобачевский писал: «Оставалось бы исследовать, какого рода перемена произойдёт от введения воображаемой Геометрии в Механику и не встретится ли здесь принятых уже и несомнительных понятий о природе вещей...» [Григорьян, 1978]. С тех пор развитие механики в частности и физики в целом шло в направлении геометризации этих наук [Уилер, 1970]. Общеизвестно, что с точки зрения общей теории относительности пространство и время образуют риманово пространство.
В статистическую физику вошла идея многомерного фазового пространства [Лошак, 2006]. В значительной степени именно по этой причине получила развитие теория динамических систем. При этом понятие динамической системы эквивалентно понятию автономной системы дифференциальных уравнений [Дубровин, 1979]. При этом оказывается, что в общем случае фазовое пространство является не евклидовым пространством, а некоторым дифференцируемым многообразием [Математическая энциклопедия. Том, 1979].
Подобное развитие науки привело к тому, что механика в настоящее время часто трактуется как геометрия неевклидовых пространств и дифференцируемых многообразий [Розенталь, 1990]. Конечно, прежде всего, речь идёт о механике материальной точки, но логика науки, несомненно, потребует обобщения всех разделов механики на случай неевклидовых пространств. Должна получить развитие неевклидова динамика твёрдого тела, а в своё время и теория неевклидовых машин и механизмов.
В настоящее время появился даже более мощный стимул разработки подобных идей. Речь идёт о создании виртуальных миров, хотя бы в чисто изобразительном плане. Подобную задачу издавна решает искусство. Достаточно вспомнить творчество М. К. Эшера и его картины «Рука с отражающим шаром», «Три шара», «Капля росы» и «Глаз» [Эшер, 2008]. Искривлённые изображения дают прекрасное представление о неевклидовой геометрии.
Искривлять изображения могут не только линзы и кривые зеркала, но и интуиция художника. Анри Бергсон, обосновывая право художника по-своему изображать мир, сказал: «Какое расположение известных нам кривых сможет когда-нибудь со штрихом карандаша великого художника?» [Куликова, 1970]. Идея искажения мира получила своё развитие в сюрреализме. «В изобразительном искусстве основные тенденции сюрреализма были представлены имитацией художественных приёмов первобытного искусства, творчества детей и душевнобольных, вычленением конкретных объектов из естественной для них среды, их «эстетизацией» путём отстранения от реальной функции или парадоксального сочетания с иными объектами» [Большая Советская Энциклопедия]. На связь сюрреализма с неевклидовыми геометриями наводят «мягкие часы» с картины Сальвадора Дали «Постоянство памяти». Таким образом, неевклидовы геометрии связаны с поиском новых эстетических идей и воплощением новых миров.
Наконец необходимость построения изображений в неевклидовых пространствах возникает в связи с некоторыми идеями естествознания. В. И. Вернадский стремился построить единую картину мироздания, используя новейшие открытия математики, физики, химии, биологии. Он писал: «Может быть в ней (Вселенной) найдутся места, где нельзя будет с точностью современной научной работы руководствоваться этой (евклидовой) геометрией» [Вернадский, 1978]. Вскоре учёный нашёл такие места очень близко: «Состояние пространства, отвечающего телу живого организма, как бы оно мало или велико не было, диссимметрично. Это проявляется в правизне и левизне - в неравенстве явлений посолонь и противосолонь». И далее: «П. Кюри совершенно правильно учёл возможность разных форм диссимметрии и выразил геометрическую структуру, связь при этом выявленную в положении, что дисимметрическое явление вызывается такою же дисимметрической причиной. Исходя из этого принципа - можно назвать его принципом Кюри - следует, что особое состояние пространства жизни обладает особой геометрией, которая не является обычной геометрией Евклида» [Вернадский, 1991]. Это предположение Вернадского получило более конкретное развитие. С направлениями конкретного развития этих идей можно познакомиться, например, в работах [34, 35].
Ограничившись перечисленными соображениями, отметим, что криволинейные координаты позволяют строить изображения, связанные с неевклидовыми геометриями. Важность этих изображений связана с разработкой некоторых видов виртуальных миров и исследованиями ряда пространственных структур реального мира. Сюда можно отнести
-
Создание иллюзии движения тел в неевклидовых пространствах, в том числе для изучения неевклидовых механизмов.
-
Создание эстетических эффектов, прежде всего, дизайнерского характера.
-
Исследование морфологии реальных объектов, построенных по принципам неевклидовых геометрий.
Рассмотрим пример преобразования форм с помощью криволинейных координат в духе д’Арси Томпсона. Отметим, что при этом криволинейные координаты играют роль своеобразной искривляющей линзы, через которую мы как бы рассматриваем изображение, построенное в декартовых координатах.


5. СОЗДАНИЕ КРИВОЛИНЕЙНЫХ СИСТЕМ КООРДИНАТ С ЗАДАННЫМИ СВОЙСТВАМИ






6. НЕКОТОРЫЕ ВОПРОСЫ МАТЕМАТИЧЕСКОГО ХАРАКТЕРА, СВЯЗАННЫЕ С СОЗДАНИЕМ КРИВОЛИНЕЙНЫХ СИСТЕМ КООРДИНАТ


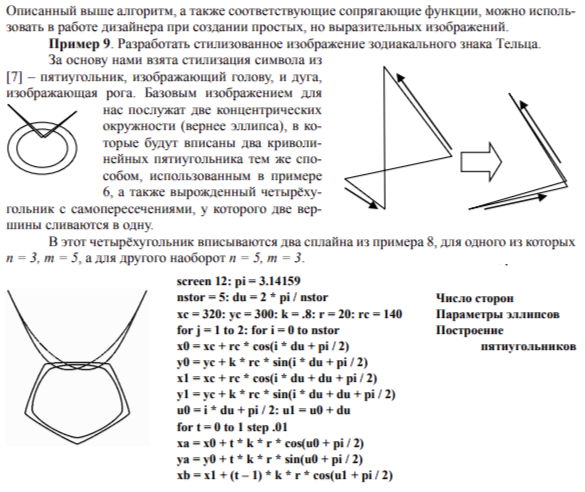
Возможна и следующая постановка задачи. Пусть задана гладкая замкнутая кривая. Необходимо построить криволинейную систему координат в области, ограниченной этой кривой. Для достаточно «хороших» кривых возможен следующий подход. На кривой выбираются четыре точки - вершины четырёхугольника. Для четырёх образовавшихся дуг строятся приближения (например, интерполяционные или сплайновые). После чего, как и в предыдущем примере, строится система координат.
Здесь прослеживается некоторое сходство с важной задачей теории функций комплексной переменной. Речь идёт о построении конформного отображения внутренности единичного круга на область, ограниченную некоторой кривой. Теорема Римана доказывает существование таких отображений [Лаврентьев, 1965]. Однако построение соответствующего отображения на практике весьма затруднительно. В частности используется приближённый эмпирический метод П. В. Мелентьева [Мелентьев].
Предлагаемый нами метод построения криволинейных координат не приводит к построению конформных отображений. Тем не менее, отметим следующее обстоятельство. Конформное отображение внутренности единичного круга на область, ограниченную некоторой кривой, переносит в эту область модель Пуанкаре геометрии Лобачевского [Прасолов, 2004]. Отображение же построенное нами переносит в ту же область геометрию Евклида. Здесь возникают определённые ассоциации с четвёртой проблемой Гильберта [Погорелов, 1974], обсуждать которые, мы не имеем возможности. Укажем лишь, что после того, как евклидова плоскость отображена в некоторую область, там возможно использование группы автоморфизмов, являющихся образами группы преобразований евклидовой плоскости. Создаётся своеобразная локальная геометрия в ограниченной области. Это открывает определённые перспективы для развития идей д’Арси Томпсона.
Кроме самостоятельной формообразующей функции криволинейные координаты в криволинейном четырёхугольнике позволяют складывать обширные координатные системы в виде своеобразной мозаики. Если на плоскости расположены два обычных четырёхугольника, имеющих общую сторону, то, искривив общую сторону по некоторой функции, остальные стороны искривляем произвольным образом и строим в каждом криволинейную систему координат. Если же плоскость или её часть покрыта мозаикой четырёхугольников, все входящие четырёхугольники можно искривить. Вычислительная сложность работы с мозаичной системой координат, конечно, возрастает. Но если необходимо создать сложную форму, работа со сложными алгоритмами становится оправданной.
Для мозаичной системы координат легко прослеживаются аналогии с гладкими многообразиями и полиэдрами. Криволинейные четырёхугольники подобны картам, но стыкуются по границам. При этом стыковка координатных линий происходит с изломом. Но возможно и построение криволинейной системы координат с гладким сопряжением координатных линий. Общая схема построения такова.
Берётся исходный прямолинейный четырёх угольник и подвергается искривлению. К нему пристраивается второй прямолинейный четырёхугольник и также подвергается искривлению. Координатные линии, переходящие друг в друга, гладко сопрягаются сплайнами на участках небольшой длины, включая и границы четырёхугольников, переходящие друг в друга. Сопряжённые координатные линии заметают новую область. К этой области пристраивается новый четырёхугольник и операция повторяется.
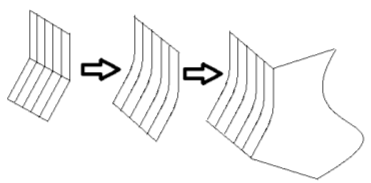
Подобным способом можно построить области различной формы, в которых введена криволинейная система координат. В том числе могут быть созданы и неодносвязные области. В «дыры» этой области могут быть вложены системы координат построенные по принципу локальных геометрий.
Выбирая в каждой области только одно семейство координатных линий, мы практически строим в этой области векторное поле. В областях с локальной геометрией таким приёмом можно получить структуры, напоминающие предельные циклы.
Векторные поля на плоскости возникают в частности при рассмотрении соответствующих систем дифференциальных уравнений. Изучение этих полей несёт существенную информацию о решениях системы, даже если они не могут быть получены в явном виде [Красносельский, 1963]. У нас векторные поля могут быть построены без дифференциальных уравнений в их классическом понимании. При этом снова намечается интересная связь с теорией динамических систем. В частности на основе понятия топологической эквивалентности векторных полей можно устанавливать связь между эмпирически построенными векторными полями и дифференциальными уравнениями [Палис, 1986].
Наконец, рассмотрим ещё один полезный способ построения криволинейной системы координат - по заранее заданным координатным линиям.


7. ИСПОЛЬЗОВАНИЕ МЕТОДА КРИВОЛИНЕЙНЫХ КООРДИНАТ В ТРЁХМЕРНОМ ПРОСТРАНСТВЕ
В компьютерной геометрии базовыми задачами, связанными с построением трёхмерных изображений, являются задача построения пространственных кривых и задача построения поверхностей. Методы решения этих задач чрезвычайно многообразны. Мы же рассмотрим только те из них, которые либо непосредственно используют выше изложенные алгоритмы, либо являются их обобщением.
Пример 32. Построить объёмное изображение стамноса (пример 11) с помощью вращения плоской кривой вокруг оси.
Описание алгоритма построения тел вращения дано в [Степанов, 2011].



8. ВЫВОДЫ
1. Представлены алгоритмы построения плоских и пространственных кривых, обладающих любой степенью морфологической сложности.
2. На основе алгоритма построения пространственных кривых предложен алгоритм построения поверхностей.
3. Все перечисленные алгоритмы могут быть использованы для создания графических редакторов, предоставляющих большие возможности конструирования кривых и поверхностей в интерактивном режиме.
4. Рассмотрены способы построения кривых в различных системах криволинейных координат.
5. Описаны разнообразные методы построения систем криволинейных координат. Они основываются как на эмпирическом подходе, так и на идеях теории функций комплексного переменного, неевклидовых геометрий и теории динамических систем.
6. Указаны перспективы применения соответствующих идей в естествознании, технике и дизайне. Даны примеры построения изображений. При этом особое внимание следует обратить на простоту используемых алгоритмов.
7. Использование различных систем криволинейных координат на плоскости открывает определённые возможности для построения прикладной морфологии плоских кривых.