Конфирматорный факторный анализ результатов вейвлет-преобразований данных мониторинга

Представлен новый метод, позволяющий проводить анализ результатов лонгитюдных исследований или данных мониторинга и выявлять факторы, влияющие на наблюдаемые характеристики, определять наличие и значимость связей между выявленными факторами, оценивать степень адекватности прикладных факторных моделей, используя статистические критерии согласия, а также новый критерий, позволяющий снять с результатов наблюдений ограничения, связанные с их вероятностным распределением.

Разработан новый подход (Куравский, Мармалюк, Баранов, Абрамочкина, Петрова, 2009; Куравский, Мармалюк, Абрамочкина, Петрова, 2009; Kuravsky et al., 2008), опирающийся на возможности вейвлет-преобразований и идентифицируемых факторных структур, который позволяет проводить конфирматорный фак торный анализ результатов лонгитюдных исследований или данных мониторинга.

Предлагаемый вариант конфирматорного факторного анализа позволяет на ходить единственное оптимальное решение задачи идентификации свободных параметров факторной модели прямым (неитерационным) методом. Процедура анализа включает в себя следующие этапы:

– преобразование исходных данных с помощью дискретного вейвлет-преобразования, позволяющего сократить размерность анализируемых временных рядов наблюдаемых характеристик с минимальными потерями полезной эмпирической информации;

– составление переопределенной системы алгебраических уравнений, выражая выборочные дисперсии и ковариации через аналогичные факторные показатели, используя модель дисперсионных составляющих;

– выявление и устранение зависимых свободных параметров модели, которые обуславливают вырожденность матрицы системы;

– решение полученной системы прямым (неитерационным) методом;

– проверку адекватности полученной модели наблюдениям, с опорой на статистические критерии согласия или на новый критерий адекватности, использующий возможности самоорганизующихся карт признаков Кохонена;

– построение заключений о статистической значимости различных компонентов прикладной модели;

– оценка факторных влияний на изменчивость наблюдаемых характеристик и показателей факторного взаимодействия (ковариации или корреляции между факторами).

Разработан новый подход (Куравский, Мармалюк, Баранов, Абрамочкина, Петрова, 2009; Куравский, Мармалюк, Абрамочкина, Петрова, 2009; Kuravsky et al., 2008), опирающийся на возможности вейвлет-преобразований и идентифицируемых факторных структур, который позволяет проводить конфирматорный фак торный анализ результатов лонгитюдных исследований или данных мониторинга.

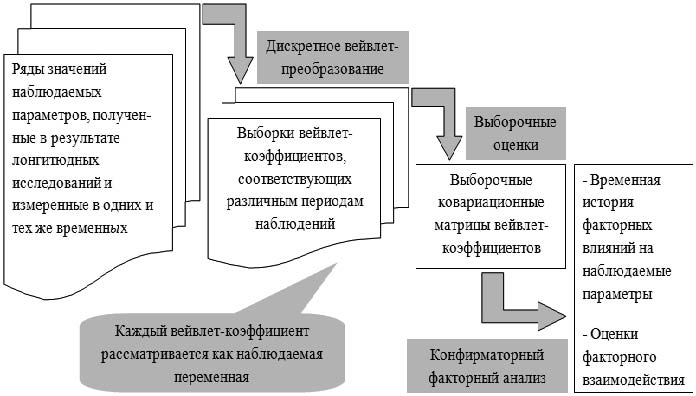
Рис. 1. Основные этапы альтернативного конфирматорного факторного анализа результатов вейвлет-преобразований

Основные этапы предлагаемого подхода представлены на рисунке 1.

Предлагаемый вариант конфирматорного факторного анализа позволяет на ходить единственное оптимальное решение задачи идентификации свободных параметров факторной модели прямым (неитерационным) методом. Процедура анализа включает в себя следующие этапы:

– преобразование исходных данных с помощью дискретного вейвлет-преобразования, позволяющего сократить размерность анализируемых временных рядов наблюдаемых характеристик с минимальными потерями полезной эмпирической информации;

– составление переопределенной системы алгебраических уравнений, выражая выборочные дисперсии и ковариации через аналогичные факторные показатели, используя модель дисперсионных составляющих;

– выявление и устранение зависимых свободных параметров модели, которые обуславливают вырожденность матрицы системы;

– решение полученной системы прямым (неитерационным) методом;

– проверку адекватности полученной модели наблюдениям, с опорой на статистические критерии согласия или на новый критерий адекватности, использующий возможности самоорганизующихся карт признаков Кохонена;

– построение заключений о статистической значимости различных компонентов прикладной модели;

– оценка факторных влияний на изменчивость наблюдаемых характеристик и показателей факторного взаимодействия (ковариации или корреляции между факторами).

Вейвлет-преобразования

Рабочие представления анализируемых временных рядов наблюдаемых параметров формируются с помощью дискретного вейвлет-преобразования, которое позволяет выявлять различия в характеристиках процесса на различных шкалах измерений и на всем протяжении интервала наблюдений.

Если исследуемый процесс есть функция одной переменной, то его вейвлетспектр – функция двух аргументов, один из которых характеризует период составляющих компонентов, а другой – смещение вычисляемых показателей вдоль оси времени. Вейвлет-преобразование имеет очевидные преимущества перед традиционным преобразованием Фурье, поскольку он обеспечивает корректные результаты в случае нестационарных процессов и содержит более полную информацию о поведении изучаемого процесса. Это сделало данный подход популярным среди исследователей разных специальностей.

Состав вейвлет-коэффициентов, используемых при анализе в качестве наблюдаемых переменных, зависит от рассматриваемой прикладной задачи и может меняться. Обычно предполагается, что число моментов времени, в которые производятся наблюдения, является степенью числа 2.

Модель дисперсионных составляющих

Для создания прикладных факторных моделей применяются модели дисперсионных составляющих (Neale, Cardon, 1992), типовой вариант которых представлен на рисунке 2.

В случае модели дисперсионных составляющих аналитические выражения для ковариаций и дисперсий вейвлет-коэффициентов Wi являются линейными:

где k и l – индексы факторов, V – дисперсии, C и C – ковариации между факторами. Линейность выражений дает возможность получать оценки свободных параметров прямым методом, который описан далее.

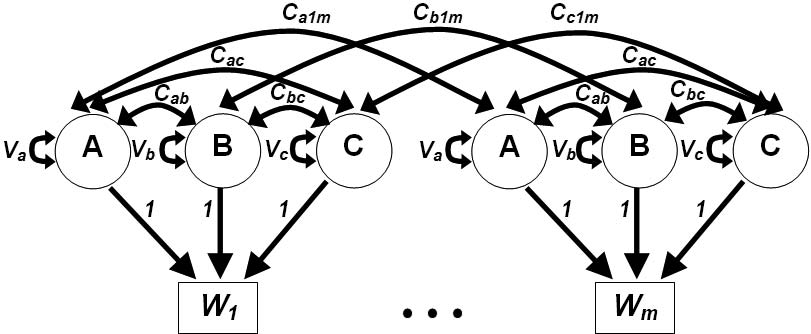
Рис. 2. Модель дисперсионных составляющих, представленная путевой диаграммой: A, B, C – латентные гипотетические факторы; Wm – вейвлет-коэффициенты, соответствующие различным периодам наблюдений

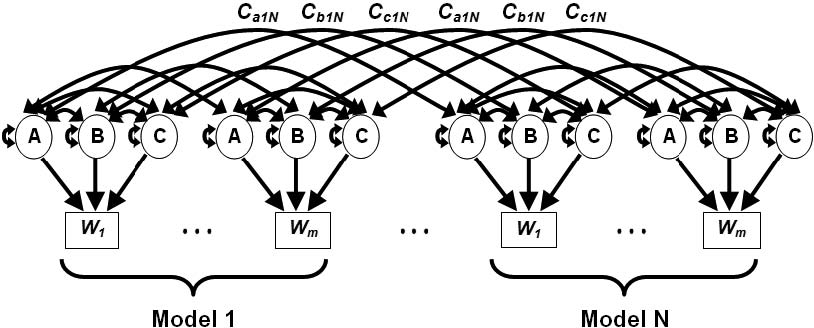
Рис. 3. Изучение факторных влияний в различных условиях: одновременный анализ различных групп моделей

Модель дисперсионных составляющих может принимать различные частные формы. Например, при изучении факторных влияний в различных условиях может быть полезен одновременный анализ различных групп моделей (рисунок 3).

Число степеней свободы, выражающее степень переопределенности модели (число дополнительных свободных параметров, которые могут быть включены в модель), является важной характеристикой возможностей ее практического применения. Сравнение числа степеней свободы для различных типов моделей (симплекс-модели, модели путевых коэффициентов и модели дисперсионных составляющих) показало, что наилучшими в смысле переопределенности обычно оказываются модели дисперсионных составляющих (Куравский, Мармалюк, Баранов, Абрамочкина, Петрова, 2009).

Идентификация свободных параметров модели

При использовании модели дисперсионных составляющих каждой наблюдаемой дисперсии и ковариации ставится в соответствие алгебраическое уравнение, которое связывает ее выборочную оценку с соответствующей прогнозируемой величиной, выраженной аналитически через неопределенные дисперсии и ковариации латентных переменных (Bollen, 1989). В результате получается система, число уравнений которой равно числу наблюдаемых дисперсий и ковариаций.

Для вычисления оценок максимального правдоподобия и проверки адекватности модели необходимо, чтобы значения наблюдаемых переменных описывались многомерным нормальным распределением, а число уравнений в исследуемой системе превышало число свободных параметров модели. Представим полученную переопределенную систему n уравнений в матричной форме: Ax = b, где A – матрица системы, коэффициенты которой определяются факторной моделью; b – вектор-столбец n выборочных дисперсий и ковариаций, определяемых результатами наблюдений; x – вектор-столбец m искомых дисперсий и ковариаций латентных переменных.

Если рассматриваемая система невырождена (т. е. ранг матрицы системы равен числу свободных параметров модели), значения наблюдаемых переменных описываются многомерным нормальным распределением, а псевдорешение

получено методом наименьших квадратов, то вектор невязки ε0 имеет многомерное нормальное распределение, а само псевдорешение является оценкой максимального правдоподобия. При этом статистика

имеет распределение χ² с n–m степенями свободы (Королюк, Портенко, Скороход, Турбин, 1985).

Выявление зависимых свободных параметров модели

Если модель, построенная для решения прикладной задачи, приводит к матрице системы, ранг которой меньше, чем число свободных параметров, то псевдорешение не может быть вычислено однозначно из-за вырожденности матрицы ATV–1A. В этом случае следует уменьшить число свободных параметров модели, исключив зависимые, и обеспечить таким образом невырожденность указанной матрицы.

Число подлежащих сокращению параметров равно дефекту матрицы ATV–1A. В наиболее полной статье, посвященной данному подходу (Куравский, Мармалюк, Баранов, Абрамочкина, Петрова, 2009), показано, как при помощи вращения базиса собственного подпространства матрицы ATV–1A можно выявить зависимые свободные параметры. Исключение выявленных параметров путем выражения их через независимые характеристики или присваивания постоянных значений обычно приводит к устранению дефекта матрицы ATV–1A.

Если эти преобразования приводят к явно неприемлемой модели, то можно, сохранив ее первоначальное представление, вычислить псевдорешение приближенно, используя итерационный метод Гаусса–Зейделя или другие подходящие методы решения систем уравнений с вырожденными матрицами.

Степень адекватности модели наблюдениям и значимость компонентов модели

Указанная статистика X2 позволяет, при условии, что рассматриваемая система невырождена, а значения наблюдаемых переменных описываются многомерным нормальным распределением, проверять гипотезу о представимости выборочных дисперсий и ковариаций, составляющих вектор b, дисперсиями и ковариациями латентных переменных исследуемой модели. Область принятия гипотезы есть X2≤χ² , где α есть уровень значимости критерия. n–m; α

Как и в традиционном конфирматорном факторном анализе, рассматриваемый метод дает возможность строить заключения о статистической значимости различных компонентов модели, используя статистические критерии согласия.

Для этого следует сравнить статистики X2 для двух моделей: полной модели, содержащей исследуемый компонент, и упрощенной модели, в которой этот компонент отсутствует. Гипотезу о том, что полная модель согласуется с результатами наблюдений, будем обозначать как Hf. Выявление степени значимости исследуемого компонента производится, если отвергать гипотезу Hf нет оснований. Сначала следует оценить свободные параметры упрощенной модели. Полученное значение статистики X2 для упрощенной модели сравнивается с аналогичной характеристикой для полной модели.

Поскольку разность указанных статистик асимптотически распределена как χ² с числом степеней свободы, равным разности в числах степеней свободы полной и упрощенной моделей, эта разность используется для проверки нулевой гипотезы Hr о том, что упрощенная модель согласуется с результатами наблюдений, против альтернативной гипотезы Hf.

Если гипотеза Hr не отвергается при заданном уровне значимости, то исследуемый компонент признается статистически незначимым и делается вывод о том, что имеющиеся данные не свидетельствуют о его влиянии на данную характеристику. Если гипотеза Hr отвергается (а гипотеза Hf принимается), то можно говорить о влиянии исследуемого компонента на эту характеристику.

Новый способ оценки степени адекватности факторных моделей

Использование метода максимального правдоподобия для идентификации значений свободных параметров и оценки степени адекватности модели предполагает проверку многомерной нормальности распределения как наблюдаемых переменных, так и компонентов вектора невязки. Эта процедура является трудоемкой и зачастую невозможной из-за малой выборки исследуемых данных. Для преодоления этой проблемы предлагается новая технология (Kuravsky et al., 2009; Мармалюк, 2010), которая использует возможности самоорганизующихся карт признаков Кохонена (Галушкин, 2000).

Оценка степени адекватности основывается на сравнении вектора невязки псевдорешения ε = Ax– bс выборкой случайных векторов невязки ε = Ax– Ax , где x – это *r*rr выборочная оценка псевдорешения, в которой определенный процент случайных компонентов выходит за рамки доверительных интервалов. Векторы невязки ε и ε подсчитываются по рассматриваемой факторной модели.

Выборка случайных векторов невязки ε используется для обучения самоор r ганизующихся карт признаков подходящей размерности, а затем для получения наборов евклидовых расстояний между векторами невязки ε r, используемых в качестве входных данных, и центрами (весовыми векторами) нейронов – победителей обученной сети.

Принимая во внимание метрику евклидового расстояния и высокую размерность векторов невязки, типичную для практических задач, по центральной предельной теореме, наборы полученных расстояний нормально распределены.

Оценки средних значений и дисперсий полученных наборов идентифицируют полученные распределения и позволяют вычислить вероятность превысить расстояние между вектором невязки псевдорешения ε и соответствующим центром нейрона-победителя, что делает возможным оценить степень адекватности модели. Сравнение распределений расстояний для различных процентных соотношений позволяет выявить наиболее правдоподобную покомпонентную структуру статистически значимых отклонений от вектора невязки псевдорешения ε.

Интерпретация результатов

Интерпретация результатов рассмотренного варианта конфирматорного факторного анализа обычно опирается на:

– оценки свободных факторных дисперсий и ковариаций;

– оценки свободных корреляций между различными факторами в одни и те же моменты времени;

– оценки свободных корреляций между одинаковыми факторами в разные моменты времени;

– оценки статистической значимости различных компонентов модели.

Соответствующие примеры могут быть найдены в статьях о применении рассмотренного подхода (Куравский, Мармалюк, Абрамочкина, Петрова, 2009; Куравский, Юревич, Мармалюк, Иванова, 2010; Мармалюк, Федулов, Куравский, Юсов, 2010).

1. Галушкин А. И. Теория нейронных сетей: Учеб. пособие. М.: ИПРЖР, 2000.
2. Королюк В. С., Портенко Н. И., Скороход А. В., Турбин А. Ф. Справочник по теории вероятностей и математической статистике. М.: Наука, 1985. Куравский Л. С.,
3. Мармалюк П. А., Баранов С. Н., Абрамочкина В. И., Петрова Е. А. Факторный анализ результатов вейвлет-преобразований лонгитюдных данных как новый метод исследования динамических характеристик сложных систем // Нейрокомпьютеры: разработка и применение. 2009. № 9. С. 5–19.
4. Куравский Л. С., Мармалюк П. А., Абрамочкина В. И., Петрова Е. А. Применение факторного анализа результатов вейвлет-преобразований для исследования динамики психологических характеристик // Экспериментальная психология. 2009. Т. 2. № 1. С. 97–111.
5. Куравский Л. С., Мармалюк П. А., Абрамочкина В. И., Петрова Е. А. Применение факторного анализа результатов вейвлет-преобразований для исследования динамики психологических характеристик // Экспериментальная психология. 2009. Т. 2. № 1. С. 97–111.
6. Куравский Л. С., Юревич А. В., Мармалюк П. А., Иванова Е. Г. Факторный анализ показателей нравственного состояния общества в европейских странах // Психологическая наука и образование. 2010. № 1.
7. Мармалюк П. А. Оценка степени адекватности факторных моделей c помощью самоорганизующихся карт признаков Кохонена // Нейрокомпьютеры: разработка и применение. 2010. № 10 (в печати).
8. Мармалюк П. А., Федулов Ю. Г., Куравский Л. С., Юсов А. Б. Применение факторных моделей для определения весовых коэффициентов в когнитивных картах на основе экспертных оценок // Сборник тезисов конференции «Ситуационные центры 2010». М.: РАГС, 2010.
9. Bollen K. A. Structural equations with latent variables. New York: John Wiley, 1989.
10. Kuravsky L.S. and Baranov S.N. Development of the wavelet-based confirmatory factor analysis for monitoring of system factors // Proc. 5th International Conference on Condition Monitoring & Machinery Failure Prevention Technologies. Edinburgh, United Kingdom. July 2008. Р. 818–834.
11. Kuravsky L. S., Baranov S. N. and Baranov N. I. Wavelet-based confirmatory factor analysis for monitoring of system factors: estimating goodness-of-fit measures with the aid of self-organizing feature maps // Proc. 6th International Conference on Condition Monitoring & Machinery Failure Prevention Technologies. Dublin, Ireland. June 2009. Р. 224–245.
12. Neale M. C., Cardon L. R. Methodology for genetic studies of twins and families // Dordrecht, the Netherlands. Kluwer Academic Publishers, 1992.