The Mediation of Arithmetic Problem-solving by Third-graders: the Procedure of “Assembling Sets”

The purpose of our study was to reveal students’ typical difficulties when performing trivial transformations of several quantities, which are to be coordinated. We have designed two tasks that required to build up the "sets", and to keep their ratio. 97 third-graders from three secondary Moscow schools were recruited for this study. The participants solved the first task individually in the written form, and afterwards there were 25 couples randomly selected to solve the similar task jointly in an oral interview with the experimenter. The analysis of the results revealed the weakness and confusion of most of the surveyed students in solving such problems. The in-depth consideration of the written works and interviews allowed us to characterize the model means, used by students, as formal or meaningful. Among them, only the “portion-by-portion” measurement of two independent quantities, performed through drawing or using the counting material, provided by the experimenter, turned out to be effective. The study showed that the source of difficulties in solving problems related to “assembling sets” is the lack of adequate model mediation, and confirmed the relevance of considering the "assembling sets problem" in the general line of development of the number concept in primary mathematics education within the framework of V.V. Davydov's theory of learning activity.

Introduction

“...And so I sat and looked at them: the boy has

two pockets, the girl has one pocket, and

some insights began to appear in my head…”

N. Nosov. “Vitya Maleev at school and at home”

The development of an approach to teaching math to primary school students is an urgent challenge. The tasks, which require coordination of changes, performed simultaneously with magnitudes of different kinds, demand special attention. The theoretical analyses of the related intellectual structures and their emergence in child’s development was begun by Piaget [14], and continued by recent research [8; 13; 15; 17; 20; 23] that pointed out specific difficulties, which students commonly experience as they try to solve such problems. We assume that these findings emphasize the complexity of the educational design, required to build up the learning situations based on the necessity to coordinate actions related to magnitude transformations.

Some feasible progress in this regard was made in the area of psychology of mathematics education in the studies [1; 5; 12; 19; 21], which followed Davydov’s view on the psychological mechanisms of number concept formation [2; 11]. The “assembling sets” task stands out among the first tasks of the primary math curriculum. It was defined as a way of comparing quantities that diverged from the direct counting of the objects they consisted of. V.V. Davydov considered the adoption of the complex procedures of counting objects by “portions” and counting portions themselves, which stem from the practical tasks of assembling sets, as the special learning task, providing for the proper number concept formation further on [3, p. 180-188; 2, p. 58-66]. The task, which demanded “mediated” comparison necessary to assess the sufficiency of the number of components for “sets”, revealed the quality of students’ orientation: either “productive” (the comparison between saliently presented quantities was mediated by the set template) or “formal” (the comparison was limited to counting separate objects) [11, p. 145-147]. The contradiction between “visual” and “conceptual”, which was embedded in the tasks’ design, exposed specific deficits in the calculation skills, acquired by first-graders.

We believe [16, 22], that it is crucial to continue the research on the potential of the assembling sets task as an initial step within the general line of number concept formation in primary school.

Organization, procedure and methods

The goal of our current study was to reveal typical difficulties in problem-solving, which students experience in arithmetic tasks, related (directly or indirectly) to assembling sets procedure and to the ratio of quantities set by these procedures. Primary school students are faced with such tasks in their third and fourth grades [7]. To assess the abilities of third graders in carrying out coordinated transformations of quantities, two tasks “about puppets and buttons” were created. They required students (along with other simple calculations) to measure components for an explicitly or implicitly set number of portions. The first part of the survey consisted of an individual written task - an answer to two basic "direct" questions from the first task:

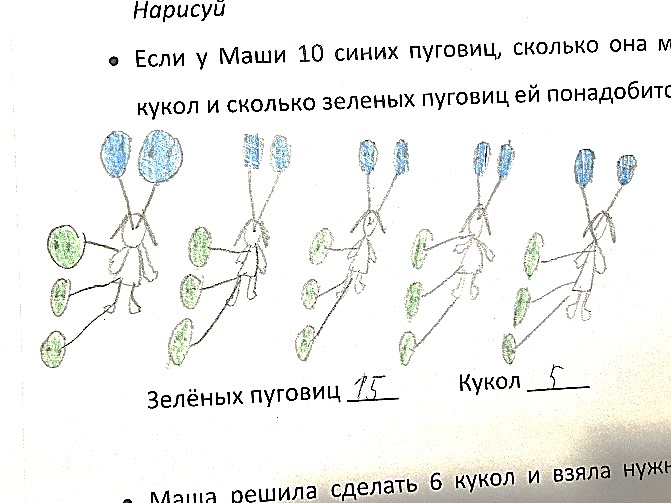
Task 1. Mary makes puppets and sews on blue buttons as their eyes. For each dress, she will sew 3 green buttons on.

(Question 1) How many blue buttons would she need if she had already taken 12 green ones for the puppets’ dresses?

(Question 2a and 2b) If Mary has 10 blue buttons, how many puppets can she make and how many green buttons does she need?

For the second part of the survey, which was an oral interview with each pair of students, the task was designed in such a way that the answers to the questions could not simply be obtained by repeating a set of buttons. It introduced the “lack” of both quantities, which were to be assembled by sets:

Task 2. Mary planned to sew puppets. Their eyes would be made of blue buttons, and they would have three green buttons sewn on each dress. Mary decided to sew 8 similar puppets and prepared the necessary number of buttons for each one. But when Mary arrived at school, she found only 14 green and 13 blue buttons in her pocket.

(Question 1) How many puppets can Mary make now?

(Question 2) How many buttons did Mary lose on her way to school?

It was necessary to group students in pairs in order to expose the process of joint problem-solving and the ways in which the provided counting materials were used, as students partially discussed them between each other.

97 third graders of three Moscow schools (43 boys and 54 girls, 9-10 years old) participated in the first part of the survey (individual written solution of the problem). 50 of these students were selected at random to solve a similar problem in the second part of the survey (oral joint solving, a total of 25 student interviews).

When completing individual tasks in the first part, students could write down their reasoning in any convenient form. There was no time limit for completing the tasks. It took our participants about 10 minutes to solve individual tasks. For the second task, each pair of students were given a leaflet with the text of the task and counting materials (blue and green tokens) for common use. The interview lasted until the students felt that they had completed the task, and that usually took between 7 and 17 minutes.

Written papers, protocols, and video recordings of interviews were used as material for analysis.

The quantitative analysis involved calculating the proportion of correct answers and analyzing the relationship between the success in solving the questions in the written assignment using conjugacy tables.

The quantitative analysis involved calculating the proportion of correct answers and analyzing the relationship between the success in solving the questions in the written assignment using conjugacy tables. The chi-square test (χ2) was calculated using the jamovi statistical package version 2.3.28.

Results and discussion

The overall success rate of solving the first task is 54%. The percentages of students who answered each question correctly are shown in Table 1.

Table 1. The success of the individual written solution to the first problem by third-graders

 The significance of the differences in the success rates of solving question 1 compared to questions 2a and 2b were calculated using conjugacy tables. Based on the analysis, we see that:

1. There is a significant direct correlation between the accuracy of answers to questions 2a and 2b (χ2 = 47.3, p < 0.0001)
2. There is a significant direct connection between the accuracy of the answers in questions 1 and 2a (χ2 = 10.8, p = 0.001)
3. There is no link between the accuracy in answers to question 1 and question 2b (χ2 = 1.26, p > 0.05).

It is remarkable that among the 13 children who correctly answered the second question about puppets (2a) and could not count the green buttons (question 2b), not a single student had answered question 1 correctly.

The range of successful answers allowed us to identify five groups of participants based on their solutions:

1. Did not solve anything: 21 students
2. Answered all the questions correctly: 28 students
3. Answered correctly only to question 2 about puppets: 13 students
4. Answered questions 2 and 3 correctly, but not question 1: 24 students
5. Answered only question 1 correctly: 8 students

Other possible combinations of right and wrong answers made up only 3 of 97 papers.

We paid special attention to the content of students’ records that accompanied their arithmetic calculations, as there was a significant number of solutions, which contained both: correct and wrong answers. In 68 cases among 194 notes that we acquired, there were traces of some data analysis by students: extracts of task conditions, tables with numbers of buttons and puppets, lines of buttons or drawings of puppets with buttons. The relationship between students' success and their use of specific means is presented in Table 2. We found that the success of solving problems was significantly related to the type of notes used by students (χ2 = 22; p < 0.001).

Table 2. The success in solving the first problem for the variety of "additional" notes used by third graders

Extracts from the task were found in the works of six students: four solutions turned out to be correct (Fig. 1a), and five were incorrect (Fig. 1b, c).

a)                                            b)                                      c)

Fig. 1. Examples of brief notes from the task, preceding right (a) and wrong (b and c) answers

Only 13 students of one of the classes that were surveyed used tables to solve the task.. It is clear that they  were trained to write down tasks in this form. Figure 2 shows examples of both successful (Fig. 2a) and unsuccessful use of these "means" (Fig. 2b).

                               a)                                                                    b)

Fig. 2. Examples of solutions using the table: a) correct; b) incorrect

 All drawings of puppets and buttons that we encountered could be divided into two categories: those in which the buttons were clearly arranged in "sets" (pictures of puppets with the buttons grouped together, the buttons circled in groups of two and three), and those with no traces of "portion by portion" calculation (rows of buttons according to their number from the task, pictures of puppets without any buttons).

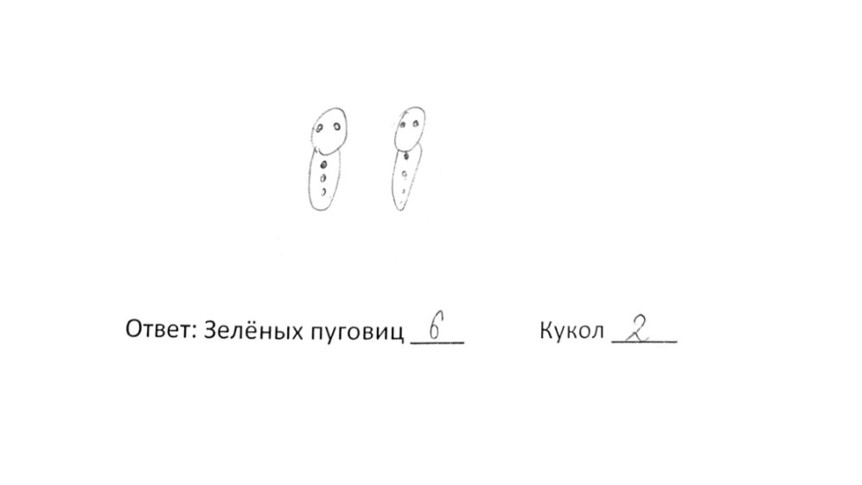
The drawing of buttons by portions was most often followed by correct arithmetic operations and answers (Fig. 3a): 23 out of the 29 cases.

                              a)                                                        b)

Fig. 3. Examples of buttons drawings accompanying correct (a) and incorrect (b) solutions

The image of buttons in rows or piles (Fig. 4), was rare (14 cases). Among the solutions illustrated in this way, there was only one correct (for example: Fig. 4a).

     a)                                                  b)

Fig. 4. Examples of button drawings without grouping them by portions accompanying the correct (a) and incorrect (b) answers.

In the second part of the survey, more than one third of the students (36%) who worked in pairs failed to answer any questions of the second task. At the same time, 60% of students answered the first question (how many puppets will Mary make?) correctly, and only 28% answered the second question (how many buttons were missing).

The analysis of the oral interview records allowed us to identify three groups of students who differed in the “strategies” of solution design and in the successful performance accordingly.

First group (9 records, 18 students) incorporates students, who could not answer any questions (did not determine the number of puppets to be made with the buttons left, or the number of buttons missing). All their solutions were reduced to random manipulations with numbers taken from the conditions or obtained during calculations. Here are some examples of these solutions:

Student A: 9 plus 8… is 17…she sewed 8 more dresses – that's 8. And 14 plus 13, that's 27. 27 divided by 3 equals 9.

Students’ M and L discussion:

M (divides 8 by 4): lost 2 buttons…

L: She couldn't possibly have lost 2 buttons. Then she wouldn't have had enough for 8 puppets. So, why would she lose 2 buttons?

M: Maybe we should multiply 4 by…

L: By 8? 32 buttons?

M: She couldn't possibly have had that much in her pocket…

L: Funny… Probably, we still need to divide 8 by 4 .

M: But she couldn't possibly have lost 2 buttons. It doesn't make any sense for her to have taken them if she is still unable to sew a puppet with them...

Student B explains why she first wanted to subtract eight from three: I thought that "minus" would be the first step, because… she had three green buttons, she decided to sew… And when they sew on... they lessen! They go to the puppet. Well, they write here... "would have three green buttons sewn on each dress"! .. Ah!.. Sewing on… is a "division"...

It is significant that, at the same time, students of the first group did not turn willingly to the counting materials prepared on the tables. Even if they were asked to solve a problem with its help, they responded that "it just confuses us". Only one pair of students were able to consistently construct the correct solution to the second question without resorting to working with the counting materials, but they failed to handle the first, easier question.

 The second group consisted of 9 pairs of students, who answered the first question correctly, but were unable to solve the second task about how many buttons had been lost. When referring to counting material, students in this group correctly spread “buttons” in portions and answered the first question. However, then they began to count the "wrong" buttons, such as extra buttons that were not actually lost, or those for four puppets that were impossible to make, etc.: laying down and recounting tokens lead them to incorrect answers. Here are some examples of such work:

Student W lays eight blue tokens in front of him: “We take eight puppets, - he circles the eight tokens with his hand, - and for each puppet there are two eyes... (separates the tokens into pairs). There will be four puppets!”

Student U and R collect four sets from 14 green “buttons” and 13 blue “buttons”, and count the remaining buttons. Student U: “That's it. She lost two green buttons and another 1-2-3-4-5 (counting them with his/her fingers)  – five blue ones”.

 The correct calculation of the number of "missing" buttons (6 records) was mostly accompanied by laying out “portions” of tokens (Figure 5). Among students that started with the formal sorting through well-learnt arithmetic operations, only those who resorted to laying out the tokens, obtained the correct answer and were able to justify it to each other and to the experimenter.

Students’ M and F discussion:

M points at the leaflet and reads it aloud: Well… She [Mary] decided to sew 8 similar puppets… that is… 8 by 3 and by 2 (points at the layed out “buttons”). We got 24 buttons and now, as she arrived at school, she found only 14, which means… 10. And three she lost… oh… I am a little lost here… I've never dealt with anything like this…

F: She had… (counts) … 16 blue and she lost 3…

M: She lost 10. There are 14 left.

M: 12…15… minus one… 14 (five triples of green "buttons" are laid out, and one "button" is put aside from the last three). And she had 16 blue eyes. She lost 3. (Students move each pair of blue buttons closer to each trio of green buttons – that makes 4 sets. Then they move another pair from the remaining blue buttons to two green buttons from the incomplete trio.)

M: That is 1-2-3-4-5 (counts “puppets” again)...

F (reads the question again): This one is not going to work! (Points at the incomplete set.) Because it is as the text goes: three! Not two, not one. That is 1-2-3-4… puppets.

M: It was simply necessary to get into it!

Fig. 5. The process of problem-solving with laying down tokens by portions (two blue “buttons” for the “eyes” and three green - for the puppets’ dresses)

The results of the survey demonstrate a number of features of third graders' use of typical techniques for solving tasks. The number and nature of mistakes made indicates, in our opinion, that some of the third graders are unable to select and perform well learnt operations with whole numbers within the first four tens’ limits.

Summarizing the results, we can say  that there should be an obvious differences between the success rate in answering the first and second questions of the written part (39% vs. 56%), and in answering the first and second questions during an oral interview (60% vs. 28%). The values necessary for the solutions were implied in the tasks’ questions either directly or indirectly. For example, 24 students failed to answer the first question of the written task, in which the "supplementary" value (the number of puppets) was not mentioned, but they succeeded in the second question, which directly required finding this very value. It's remarkable though that the number of puppets found correctly in question 2a did not necessarily lead to correct calculation of the number of buttons (13 participants). Apparently, these students were not able to handle “the third value” (the number of puppets) appropriately: though they found it, they could not implement it into calculations directly.

The divergence in the number of correct answers to the oral interview questions indicates the actual complexity of the situation created by the task. The first question (about puppets) required measuring given quantities of blue and green buttons "directly" in the correct proportions, whereas the second question (counting missing buttons) implied preliminary measurement by "portions" to build up an exact number of buttons for eight “would-be” puppets as a solution mediator.

The drawing of buttons grouped into portions for each puppet has proven to be the most effective means (79% of correct answers) among the typical additional records used by students. The success rate for solving problems using brief and tabular summaries of task conditions did not significantly differ from that of students who provided no explanations for the solutions they compiled and the answers they derived (44% and 38% compared to 44%, respectively, χ² = 0.28, p>0.05).  The presence of puppets-drawings without buttons or rows of buttons with no portions made visible is significantly associated with incorrect solutions (χ² = 7.26 p < 0.01), suggesting that the pictorial representation of combined portions is more productive than a formal recording of quantities.

The oral interview in the second part of the survey allowed us to clarify the specific content of a student’s action as related to drawing schemes of puppets, which provided significant advantages in solving problems individually in the first part. The counting material offered to students did not in itself guarantee that its model functions in relation to the analysis of the task situation will be performed automatically. However, they were quite suitable for this purpose, allowing one to "materialize" an implicit "third" value (the number of button portions), on which the decision depended directly. Thus, students that were solving the task had the opportunity to perform an adequate orientation action, which would mediate necessary calculations, while considering both explicit and implicit conditions (combining different buttons into portions according to the required number of toys).

Those third graders (6 pairs out of 25) who successfully solved the entire problem by dividing the counting materials into portions, apparently imparted the tokens with the required model functions. The incorrect solutions were often associated with attempts to extract a ready-made solution "directly" from counting "buttons", which they had placed on the table randomly. Only those students, who started placing the "buttons" in portions, were able to find and correct the mistakes they had made at the beginning and therefore, they managed to succeed at least with the first question. The participants' appeal to the coordinated counting “by portions” required here, revealed the implicit ratio of calculated values, and obviously allowed them to overcome the difficulties of "common counting".

Conclusion

The results confirm our assumption that the modeling actions, relying on assembling sets procedure, are crucial for solving the tasks we designed. It is the lack of mastery of mediative functions of these actions that leads students to go around even in the basic arithmetic tasks. They rely on a random selection of numbers and operate with them.

The tasks we designed required precise calculation and coordination of independent changes of quantities of different kinds interrelated by the script. To coordinate these changes they had to measure each amount by appropriate portions and estimate  the number of these portions based on the required number of objects (in our case, dolls with two types of buttons). The identification of this “third” value, which is either explicitly or implicitly provided in the task conditions, plays a significant orientating function in determining the order of actions and applying arithmetic operations.

The ways in which some students were using both their own and given supplementary means (diagrams, drawings, counting materials) revealed their helplessness in solving “critical” tasks where numbers could not be used directly to obtain an answer. The calculations they performed could be characterized as “formal”. The “meaningful” method would imply modeling materials and actions, but for third graders, the need for such a method was not obvious. Familiar formal techniques for defining “necessary” operations directly based on task data (e.g., tables) did not assist in finding the correct answer. Apparently previous training was not focused on appropriate model reconstruction of the matter, which would have enabled students to design their own solutions with regard to implicitly set conditions.

It is remarkable that consideration of students’ typical mistakes in arithmetic problems solving gradually leads researchers to the analysis of the "deficits" in using “model supports” and the prerequisites for their assimilation by primary school students [9; 10; 11; 19]. Treating model objects only as salient illustrative material has been subject to significant criticism [3; 4], but unfortunately, it is still present in the methodological support for primary education.

In general, the results of the current research, as well as those of many others in this field [6; 19; 20], confirm the importance of the psychological and pedagogical study of the ways to include the modeling content under consideration to the elementary course of mathematics. This special content is relevant within co-measurement of quantities required in “assembling sets” task. The organization of the corresponding actions with the appropriate material is meaningful for primary math learning while students are introduced to working with magnitudes. Significant prospects here are granted by the logical-genetic analysis of the learning actions’ structure and content, related to students’ acquisition of the learning material. The identification and description of the essential model mediation’s functions is an urgent challenge for psychological research on the number-concept formation in primary school.

1. Aleksandrova E.I. Matematika. 1 klass. Uchebnik. Kniga 1 [Mathematics. 1st grade. Textbook. Book 1]. Moscow: BINOM. Laboratoriya znanii, 2019. 160 p. (In Russ.).
2. Davydov V.V. Analiz stroeniya scheta kak predposylka postroeniya programmy po arifmetike [Analysis of the structure of counting as a prerequisite for developing an arithmetic curriculum]. Voprosy psikhologii uchebnoi deyatel'nosti mladshikh shkol'nikov = Psychological issues of learning activity of junior school students. Moscow: APN RSFSR, 1962, pp. 50–184. (In Russ.).
3. Davydov V.V. Vidy obobshcheniya v obuchenii [Types of generalization in education]. Moscow: Pedagogika, 2000. 480 p. (In Russ.).
4. Davydov V.V., Vardanyan A.U. Uchebnaya deyatel'nost' i modelirovanie [Learning activity and modelling]. Erevan: Luis, 1981. 220 p. (In Russ.).
5. Davydov V.V., Gorbov S.F., Mikulina G.G. Matematika. 1 klass. Uchebnik. FGOS [Mathematics. 1st grade. Textbook. FGOS]. Moscow: Prosveshchenie/Binom, 2022. 160 p. (In Russ.).
6. Lobanova A.D., Vysotskaya E.V., Yanishevskaya M.A. Vstroennaya diagnostika model'nogo oposredstvovaniya u uchashchikhsya nachal'noi shkoly: zadacha komplektovaniya [Integrated diagnostics of model mediation in primary school students: the task of assembling sets]. In A.V. Borovskikh (ed.). Deyatel'nostnaya pedagogika i pedagogicheskoe obrazovanie: Sbornik dokladov uchastnikov IX i X Mezhdunarodnykh konferentsii DPPO-2021 (g. Voronezh, 10–14 sentyabrya 2021 g.); DPPO-2022 (g. Voronezh, 9–13 sentyabrya 2022 g.) [Activity pedagogy and pedagogical education: A collection of reports of participants of the IX and X International Conferences of the DPP-2021; DPP-2022] Moscow: MAKS Press, 2022, pp. 66–72. (In Russ.).
7. Moro M.I. et al. 3-i klass. Uchebnik. V 2 chastyakh. Ch. 2 [Mathematics. 3rd grade. Textbook. In 2 parts. Part 2]. Moscow: Prosveshchenie, 2023. 112 p. (In Russ.).
8. Rubtsov V.V. Organizatsiya sovmestnykh deistvii i razvitie intellekta u detei [Organization of joint actions and development of intelligence in children]. In Rubtsov V.V., Ulanovskaya I.M. (eds.). Sovmestnaya uchebnaya deyatel'nost' i razvitie detei. Kollektivnaya monografiya. Glava 3 [Joint educational activities and child development. Collective monograph. Chapter 3]. Moscow: FGBOU VO MGPPU, 2021, pp. 48–69. (In Russ.).
9. Chudinova E.V. Initsiativnaya opora shkol'nikov na skhemy v samostoyatel'nom reshenii zadach [How Students Construct Scaffolds by Using Drafts for Solving Tasks]. Psikhologicheskaya nauka i obrazovanie = Psychological Science and Education, 2021. Vol. 26, no. 2, pp. 66–77. DOI:10.17759/pse.2021260206 (In Russ., аbstr. in Engl.).
10. El'konin B.D. Sovremennost' teorii i praktiki Uchebnoi Deyatel'nosti: klyuchevye voprosy i perspektivy [Modern Era of the Theory and Practice of Learning Activity: Key Issues and Perspectives]. Psikhologicheskaya nauka i obrazovanie = Psychological Science and Education, Vol. 25, no. 4, pp. 28–39. DOI:10.17759/pse.2020250403 (In Russ., аbstr. in Engl.).
11. El'konin D.B., Davydov V.V. Vozrastnye vozmozhnosti usvoeniia znanii (mladshie klassy shkoly) [Age capabilities in knowledge acquisition (early school grades)]. Moscow: Prosveshchenie, 1966. 442 p. (In Russ.).
12. Coles A. Commentary on a special issue: Davydov’s approach in the XXI century. Educational Studies in Mathematics, 2021. Vol. 106(3), pp. 471–478. DOI:10.1007/s10649-020-10018-9
13. Hilton A., Hilton G. Primary school teachers implementing structured mathematics interventions to promote their mathematics knowledge for teaching proportional reasoning. Journal of Mathematics Teacher Education, 2019. Vol. 22(6), pp. 545–574. DOI:10.1007/s10857-018-9405-7
14. Inhelder B., Piaget J. The growth of logical thinking from childhood to adolescence: An essay on the construction of formal operational structures. Developmental Psychology, 1958. Vol. 22, Psychology Press. 356 p. DOI:10.1037/10034-000
15. Lamon S.J. Teaching fractions and ratios for understanding: Essential content knowledge and instructional strategies for teachers. Routledge, 2020. 294 p. DOI:10.4324/9780203803165
16. Lobanova A., Rekhtman I., Vysotskaya E., Yanishevskaya M. Towards Proportionality within Developmental Instruction Approach: The First Steps. In Michelsen C. et al. (eds.). Mathematics and Its Connections to the Arts and Sciences (MACAS) 15 Years of Interdisciplinary Mathematics Education. Mathematics Education in the Digital Era. Vol. 19. Springer, Cham, 2022, pp. 205–229. DOI:10.1007/978-3-031-10518-0_11
17. Lobato J., Ellis A. Developing Essential Understanding of Ratios, Proportions, and Proportional Reasoning for Teaching Mathematics: Grades 6–8. Reston: National Council of Teachers of Mathematics, 2010. 88 p.
18. Polotskaia E., Fellus O.O., Cavalcante A., Savard A. Students’ problem solving and transitioning from numerical to relational thinking. Canadian Journal of Science, Mathematics and Technology Education, 2022. Vol. 22(2), pp. 341–364. DOI:10.1007/s42330-022-00218-1
19. Polotskaia E., Savard A. Some multiplicative structures in elementary education: A view from relational paradigm. Educational Studies in Mathematics, 2021. Vol. 106, pp. 447–469. DOI:10.1007/s10649-020-09979-8
20. Simon M.A. Developing a concept of multiplication of fractions: building on constructivist and sociocultural theory. In Norton A., Alibali M.W. (eds.). Constructing Number: Merging Perspectives from Psychology and Mathematics Education, Research in Mathematics Education. Springer, Cham, 2019, pp. 193–212. DOI:10.1007/978-3-030-00491-0_9
21. Venenciano L., Polotskaia E., Mellone M., Radford L. An introduction to multiple perspectives on Davydov’s approach in the XXI century. Educational Studies in Mathematics, 2021. Vol. 106, pp. 323–326. DOI:10.1007/s10649-021-10040-5
22. Vysotskaya E., Lobanova A., Rekhtman I., Yanishevskaya M. The challenge of proportion: does it require rethinking of the measurement paradigm? Educational Studies in Mathematics, 2021. Vol. 106(3), pp. 429–446. DOI:10.1007/s10649-020-09987-8
23. Watson A., Jones K., Pratt D. Key ideas in teaching mathematics: Research-based guidance for ages 9-19. Oxford University Press, 2013. 272 p.