Об адекватности психофизических измерений

Законы Фехнера и Стивенса являются основными психофизическими законами. Трудность заключается в том, что законы Фехнера и Стивенса не совпадают. Предлагается много способов объяснить это несовпадение. Но не решена проблема адекватности психофизических измерений. Дело в том, что Фехнер и Стивенс по-разному определяют способ измерения. Но только определение Стивенса было принято за основу в репрезентативной теории измерений, которая развивалась вначале как теория психофизических измерений. В репрезентативной теории существует ряд недостатков. В частности, отсутствует встроенный механизм проверки адекватности результатов измерения. Поэтому возникают сомнения в количественном характере психологических атрибутов. И остается нерешенным вопрос относительно правомерности применения закона Фехнера. С целью развития количественной теории измерений была предложена теория рейтингов. С позиций теории рейтингов, оба психофизических закона равноправны и отличаются способом измерения. Показано, что результаты измерения, полученные разными способами, в определенном смысле эквиваленты. Теоретическим обоснованием эквивалентности является изоморфизм алгебраических структур. Такое решение проблемы Фехнера—Стивенса является конструктивным, так как содержит возможность экспериментальной проверки адекватности результатов измерения. Также рассматривается пример оценки адекватности математической модели.

Введение

Традиционный подход в психофизике акцентирует внимание на выявлении количественных закономерностей сенсорного процесса [5]. Существуют два способа измерения интенсивности ощущений, которым соответствуют закон Фехнера [12] и закон Стивенса [19]. Исследователи по-разному объясняли различие между законами Фехнера и Стивенса. Достаточно полно история вопроса приведена в работах [10; 18; 13].

Впервые использовать субъективные измерения предложил Фехнер (1860) [9]. Метод Фехнера был основан на регистрации «едва заметных различий» между ощущениями, связанными с парами стимулов, например, двумя звуками разной интенсивности. Тогда можно определить количество едва заметных различий меду любыми двумя парами стимулов (разность значений). Метод Фехнера позволил сформулировать психофизический закон в виде:

u = l1ln(q),

где q — значения величины, полученные объективно, u — значения величины, полученные субъективными методами измерения, l1 — постоянная, l1 > 0.

Будем рассматривать объекты измерения w1, w2, …, wn. Закон Фехнера для разности субъективных значений можно записать в форме:

ui — uj = l1ln(qi / qj), (1)

где i, j = 1, 2, …, n, n > 2, ui = u(wi), qi = q(wi), qi — объективные значения, qi > 0; ui — субъективные значения величины (полученные субъективными методами измерения).

Стивенс (1957) не был согласен с Фехнером и определил измерение как «присвоение числительных объектам или событиям в соответствии с правилами» [20]. Стивенс предложил заменить закон Фехнера психофизическим законом вида:

v = сql2,

где с, l2 — постоянные, с > 0, l2 > 0. Закон Стивенса для отношение субъективных значений может быть записан в виде:

ln(vi / vj) = l2ln(qi / qj), (2)

где i, j =1, 2, …, n, l2 — постоянная, vi= v(wi), qi= q(wj), qi — объективные значения, qi > 0, vi — субъективные значения величины; vi > 0. Считаем, что значения ui в формуле (1) определены с точностью до произвольной аддитивной постоянной, а значения vi в формуле (2) — с точностью до произвольной мультипликативной постоянной.

В работе [13] делается вывод, что до сих пор в психофизике существует сложная проблема, заключающаяся в том, что уравнения основных психофизических законов не совпадают. Противоречие состоит в том, что каждый из законов описывает реакцию человека на ощущение внешних раздражителей, но их функциональные формы различны. Согласование этих двух законов является предметом длительных дебатов, но никакого решения, которое удовлетворило бы исследователей, найдено не было. Тем не менее определение измерения Стивенса было принято за основу при разработке психометрических методов в репрезентативной теории измерений [11].

С математической точки зрения, репрезентативная теория базируется на разделе теории множеств, посвященном системам с отношениями. У репрезентативной теории существует ряд недостатков:

1) отсутствует встроенный механизм проверки адекватности результатов измерения;

2) остается нерешенным вопрос о причинах несовпадения основных психофизических законов;

3) остаются нерешенными вопросы выбора шкалы измерения.

Так, Д. Мишель говорит о невозможности рассматривать результаты измерений априори количественными [15]. Это будет верно только тогда, когда такое предположение будет подтверждено некоторой экспериментальной проверкой. Поэтому Д. Мишель достаточно негативно оценивает достижения психофизики [16]. Р.Д. Люс считает попытки Г.Т. Фехнера и С.С. Стивенса поставить субъективные измерения интенсивности физических сигналов на прочную научную основу едва ли удовлетворительными [14].

Кроме того, наличие двух психофизических законов приводит к расхождениям в результатах измерения, а именно к получению различныx субъективных значений признака. Для объяснения этой проблемы были предложены различные модификации законов Фехнера и Стивенса [7; 8]. Другой подход состоял в том, чтобы рассматривать закон Фехнера и закон Стивенса как асимптотику одного общего закона [12; 17]. В работе Ю.М. Забродина [1] в формулу закона С. Стивенса вводится показатель, характеризующий степень осведомленности респондента. Обобщенный психофизический закон Забродина позволяет объяснить различие между законами Стивенса и Фехнера, но требует дополнительной измерительной информаци и проверки. В работах И.Г. Скотниковой развивается концепция субъектной психофизики, которая базируется на достижениях количественного психофизического анализа Г. Фехнера и С. Стивенса [5].

С целью развития количественного анализа предлагается вариант теории измерений — теория рейтингов [3; 4]. В репрезентативной теории измерений результат измерений — это значение измеряемой величины, полученное путем проведения измерений. Результаты измерений должны соответствовать шкале измерений [11]. В теории рейтингов результат измерения — это разность или отношение значений, которые получают в результате сравнения пары объектов по величине [4].

Математической основой теории рейтингов является не теория множеств, а теория категорий. Теория рейтингов имеет определенные преимущества перед репрезентативной теорией измерений:

1) включает способ экспериментальной проверки адекватности результатов измерения;

2) в теории рейтингов психофизические законы Фехнера и Стивенса эквивалентны;

3) выбор шкалы измерения сводится к выбору способа измерения.

В настоящей работе предлагается применять определение рейтинга для проверки адекватности результатов психологических измерений.

Анализ законов Фехнера и Стивенса

Под результатом измерения будем понимать разность значений ui — uj или отношение значений vi / vj и говорить о двух основных способах измерения.

Разность значений можно найти с помощью закона Фехнера (1), отношение значений — на основании закона Стивенса (2). В этом случае результаты измерения (разность и отношение значений) связаны между собой формулой:

(ui — uj) = lln(vi / vj), (3)

где i, j = 1, 2, …, n; ui и vi — субъективные значения Фехнера и Стивенса, l = l1 / l2, l1 , l2 — постоянные. Равенство (3) непосредственно следует из закона Фехнера (1) и Стивенса (2).

Отображение u = lln(v) является изоморфизмом множества положительных действительных чисел с операцией деление на множество действительных чисел с операцией вычитание. С точки зрения алгебры изоморфные структуры можно не различать [2]. Равенство (3) означает, что изоморфизм преобразует одни результаты измерения в другие. Такие результаты измерения будем называть эквивалентными. Для иллюстрации рассмотрим частный случай, когда величина измеряемых объектов изменяется равномерно [3].

Пример. Пусть значения площади кругов w1, w2, …, w6 (табл. 1) изменяются равномерно, и отношение значений площади двух последовательных кругов равно двум: vi+1 / vi = 2, vi — значение площади круга, i = 1, 2, …, 5.

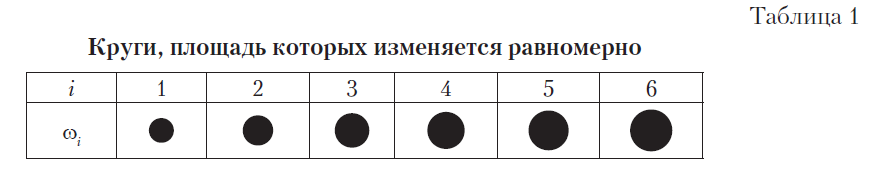
Присвоим каждому объекту порядковый номер ui = i и найдем результат измерения по формуле ui — uj = i — j. Измерение вторым способом проведем, используя заданные отношения. Тогда для результата измерения получим выражение vi / vj = 2i / 2j, где i, j = 1, 2, …, 6. Результаты измерения эквивалентны, так как определен изоморфизм (3), где l = 1 / ln(2).

Из примера следует, что измерения можно производить как субъективными, так и объективными методами, а метод Фехнера можно применять к любым объектам, величина которых изменяется равномерно. Для двух способов измерения можно получить значения величины (табл. 2.),

Таблица 2

Значения, полученные двумя способами

ui	1	2	3	4	5	6
vi	2	22	23	24	25	26

для которых изоморфизм u = lln(v), где l = 1 / ln(2), устанавливает взаимно однозначное соответствие между значениями величины.

Результаты измерения, полученные способом Фехнера и Стивенса, эквивалентны. Следовательно, зная отношение значений в законе Стивенса, можно рассчитать разность значений в законе Фехнера по формуле (3), и наоборот. Возможность обоснованно предсказать результат измерения является наиболее важным аргументом в пользу такого решения проблемы Фехнера—Стивенса.

Определение рейтинга

Прежде чем сформулировать определение рейтинга приведем пример изоморфизма в психологии. Изоморфизм алгебраических структур не означает, что для наблюдателя эти структуры существуют и воспринимаются как изоморфные. Например, в современной психофизике отличают поведение реального и идеального наблюдателя [5]. Поэтому проанализируем классические эксперименты по измерению громкости звука [6]. Покажем, что два способа субъективного измерения громкости существуют и результаты измерений двумя способами связаны условием изоморфизма (3). В этом случае можно говорить, что субъективные измерения позволяют обнаружить существование двух изоморфных алгебраических структур.

Для простоты изложения будем сравнивать между собой громкость звуков различной интенсивности I, которые имеют стандартную частоту колебаний 1000 Гц. Существуют две основные единицы для субъективного измерения громкости звуков — фон и сон. Единица измерения громкости «фон» связана с законом Фехнера. Единица измерения громкости «сон» связана с законом Стивенса.

Для измерения методом Фехнера вводят единицу измерения — величину ощущения едва заметного различия (ЕЗР). Далее измеряют расстояние на оси ощущений в количестве ЕЗР. Существуют многочисленные эксперименты, которые подтверждают, что субъективное восприятие громкости подчиняется закону Фехнера. Поэтому на основании закона Фехнера введена стандартная единица измерения громкости звука — фон [6]. Закон Фехнера в этом случае выглядит так: u = 10lg(I / I0), где u — громкость звука в фонах, I — интенсивность звука, I0 — порог слышимости. С помощью закона Фехнера можно сравнить громкость двух звуков с интенсивностью I1 и I2 по формуле:

(u2 — u1) =10lg(I2 / I1). (4)

Здесь (u2 — u1) — разность субъективных оценок громкости в фонах.

Для измерения громкости методом Стивенса испытуемому предъявляют два тона, которые он должен сравнить с точки зрения громкости — во сколько раз один из них кажется ему громче другого. Показано, что зависимость психологической оценки громкости v от физической интенсивности звука I описывается законом Стивенса. Громкость в сонах находится по приближенной формуле: v = kI 0,3, где k — постоянная. Сон — это единица измерения громкости, предложенная С. Стивенсом в 1936 г. и используемая до сих пор [6]. Используя закон Стивенса, отношение громкости двух звуков с интенсивностью I1 и I2 можно найти по формуле:

lg(v2 / v1) = 0,3lg(I2 / I1). (5)

где (v2 / v1) — отношение субъективных оценок громкости в cонах.

Считают, что шкала сонов связана со шкалой фонов однозначной зависимостью: при каждом увеличении уровня громкости на 10 фон число единиц сон примерно удваивается [6]. Действительно, из формул (4) и (5) непосредственно следует равенство:

(u2 — u1) = 10,034.lоg2(v2 / v1), (6)

где (u2 — u1) — изменение громкости звуков в фонах, (v2 / v1) — изменение громкости тех же звуков в сонах. Равенство (6) совпадает с условием (3).

Вывод. Субъективное измерение громкости можно проводить в шкале сонов и шкале фонов. Причем результаты измерений связаны условием изоморфизма (6). Более того, такие шкалы давно и успешно используют для стандартизации способов измерения громкости. Тем самым получено подтверждение, что субъективные методы измерения позволяют установить существование изоморфных алгебраических структур. Теперь сформулируем определение рейтинга.

Определение. Будем одновременно рассматривать два способа измерения. Для этого равенство (3) заменим двумя выражениями:

Rij = l1ln(vi / vj), (7)

Rij = l2(ui — uj), (8)

где i, j = 1, 2, …, n. Отображения (7) и (8) будем называть рейтингом.

В зависимости от способа измерения значения рейтинга Rij можно найти по формулам (7) или (8). Значения рейтинга не зависят от способа измерения. Это означает, что рейтинг и есть та величина, которую фактически оценивает респондент двумя способами. Подчеркнем, что определение рейтинга не сводится к просто замене переменных, а опирается на такое фундаментальное понятие алгебры, как изоморфизм.

Проверка адекватности

Респондент может ошибаться или вводить в заблуждение. Для проверки точности ответов респондента проведем измерение двумя способами. Рассмотрим пример анализа реальных данных.

Пример. Пусть требуется субъективно измерить площадь шести кругов w1, w2, …, w6 (табл. 1).

Таблица 3

Результаты измерения

ui – u4	vi / v1
-7	1
-6	1,5
-2	2,25
0	2,75
2	3,25
4	3,75

Ответы респондента на вопросы представлены в табл. 3. Результаты измерения первым способом получены методом семантического дифференциала. Респондент сравнивает все объекты с фиксированным и указывает целое число в диапазоне от -8 до 8. Число должно соответствовать степени превосходства одного объекта над другим. В качестве фиксированного элемента можно выбрать любой объект. В данном случае такой объект имеет четвертый номер. Результаты измерения находятся в первом столбце таблицы 3. Например, число -7 в первом столбце означает, что первый элемент на семь единиц меньше четвертого. Чем больше число отличается от нуля, тем больше превосходство. Для нахождения результатов измерения вторым способом фиксируем первый объект. Ответы респондента находятся во втором столбце. В частности, респондент считает, что второй элемент больше первого в полтора раза.

Значения рейтинга рассчитывались по формулам (7) и (8) и находятся в первом и втором столбце табл. 4. Постоянные масштаба выбраны таким образом, чтобы размах варьирования рейтинга равнялся пяти.

Таблица 4

Значения рейтинга

Ri4(1)	R i1(2)
0,00	0,00
0,45	1,53
2,27	3,07
3,18	3,83
4,09	4,46
5,00	5,00

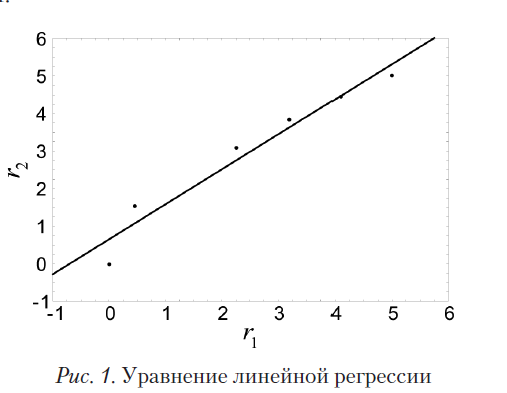
Значения рейтинга не должны зависеть от способа измерения. Для анализа точности ответов респондента можно использовать уравнение регрессии: r1 = b0 + b1 r2, — построенное по эмпирическим значениям рейтинга Ri4(1) и R i1(2), табл. 4. По критерию Стьюдента оценка параметра b1= 0,91 является значимой (достигаемый уровень значимости p = 0,00036), оценка параметра b0 = 0,85 незначима (достигаемый уровень значимости p = 0,20). Значимость коэффициента уравнения регрессии b1 подтверждает взаимную адекватность результатов измерений. Незначимость коэффициента b0 свидетельствует об отсутствии существенной систематической ошибки. Поэтому принимаем гипотезу о взаимной адекватности результатов измерения. Далее проводим анализ графика уравнения регрессии (рис. 1), который указывает на наличие небольшой систематической ошибки в результатах измерения.

Такой предварительный анализ, несмотря на небольшой объем статистических данных, позволяет выполнить индивидуальный контроль данных каждого испытуемого и избежать грубых ошибок при проведении тестирования группы испытуемых.

Заключение

В работе показано, что психофизические измерения можно проводить двумя способами. Причем результаты измерения разными способами эквивалентны. Теоретическим обоснованием эквивалентности является изоморфизм соответствующих алгебраических структур, который подтверждается основными положениями законов Фехнера и Стивенса. Анализируется пример субъективного измерения, в котором использованы разные способы измерения. Пример включает процедуру проверки адекватности результатов измерений.

1. Забродин Ю.М., Лебедев А.Н. Психофизиология и психофизика. М.: Наука, 1977.
2. Курош А. Г. Лекции по общей алгебре. М.: Физматлит, 1973. 400 с.
3. Романчак В.М. Измерение нефизической величины // Системный анализ и прикладная информатика. 2017. № 4. С. 39—44.
4. Романчак ВМ. Субъективные измерения (теория рейтингов). Журнал Белорусского государственного университета. Философия. Психология. 2020. № 3. С. 87—98.
5. Скотникова И.Г. Психология сенсорных процессов. Психофизика // Психология XXI века / Под ред. В.Н. Дружинина. М.: Per Se, 2003. С. 117—168.
6. Линдсей П., Норман Д. Переработка информации у человека: пер. с англ. М.: Мир, 1974.
7. Cook M.L. The Power Law as a Special Case of Fechner’s Law // Perceptual and Motor Skills. 1967. Vol. 25. № 10. P. 51—52.
8. Ekman G. Is the power law a special case of Fechner’s law? // Perceptual and Motor Skills. 1964. Vol. 19. № 3. P. 730.
9. Fechner G.T. Elements of psychophysics (H. E. Adler, Trans.) New York: Holt, Rinehart and Winston, 1966. (Original work published 1860)
10. Gescheider G.A. Psychophysics: The Fundamentals, 3rd Edition. London, Psychology Press, 2015. 446 p.
11. Grondin S. Psychology of Perception. Springer International Publishing, Switzerland, 2016. 156 p. DOI:10.1007/978-3-319-31791-5
12. Krantz D.M., Luce R.D., Suppes P., Tversky A. Foundation of measurement. Vol 1. N.Y.: Academic Press, 1971.
13. Krueger L.E. Reconciling Fechner and Stevens: Toward a united psychophysical law // Behavioral and Brain Sciences. 1989. Vol. 12. № 2. P. 251—267.
14. Lubashevsky I. Psychophysical laws as reflection of mental space properties // Phys Life Rev. 2019. Vol. 31. P. 276—303.
15. Luce R.D. A way to blend Fechner and Stevens // Fechner Day Proceedings of the seventeenth annual meeting of the international society of psychophysics. / In E. Sommerfeld, R. Kompass, & T. Lachmann (Eds.). Pabst Science Publishers, 2001. P. 28—35.
16. Michell J. Is psychometrics pathological science? // Measurement: Interdisciplinary Research & Perspective. 2008. Vol. 6. № 1. P. 7—24.
17. Michell J. Measurement in Psychology: A Critical History of a Methodological Concept. Cambridge, England: Cambridge University, 1999. 268 p.
18. Norwich K.H. & Wong W. Unification of psychophysical phenomena: The complete form of Fechner’s law // Perception & Psychophysics. 1997. Vol. 59. № 6. P. 929—940.
19. Stevens S.S. Mathematics, measurement, and psychophysics // Handbook of experimental psychology / Ed. S.S. Stevens. New York: Wiley, 1951.
20. Stevens S.S. On the Psychophysical Law // Psychological Review. 1957. Vol. 64. № 3. P. 153—181.

PlumX

Метрики публикации