1. ВВЕДЕНИЕ
Говоря о различных методах, используемых в прикладных количественных отраслях, связанных с проведением и анализом измерений, (это касается и биологии, и психологии, и других гуманитарных и социальных наук) можно выделить два подхода. С одной стороны - это прикладная статистика, базирующаяся на строгих критериях, обеспокоенная в первую очередь доказательством достоверности и надежности результатов, а с другой стороны, системная динамика, главный акцент, делающая на использовании нелинейных моделей. Поскольку линейные зависимости в реальной жизни встречаются крайне редко, да и то на ограниченных пространственных или временных интервалах, возникает острая необходимость перенести достоинства «линейной» статистики (надежность, достоверность) на более реалистичную теорию нелинейных динамических систем.
Очень часто для того чтобы смоделировать (описать, а потом исследовать) сложный феномен или процесс будь то живая или неживая природа, отдельный человек, социум достаточно бывает использовать несложные с точки зрения математики уравнения. Еще Пуанкаре
установил, что три простых тела взаимодействуя между собой на основании строго определенных уравнений порождают чрезвычайно сложную систему, предсказать однозначно поведение которой невозможно. Дело тут не в отсутствии каких-то знаний или несовершенстве вычислительной техники, а в принципиальной математической неопределенности [Пуанкаре, 1910].
Желание возможно более точно прогнозировать поведение, результаты функционирования сложных систем, имеющих самую разную природу, способствует возникновению и развитию объясняющих теорий, проведению исследований. Биологи, социальные исследователи заимствуют идеи и методы из наук о неживой природе: физики, химии. Было доказано, что детерминированность и предсказуемость не одно и то же даже в простой системе, которую можно описать тремя дифференциальными уравнениями. Если в такой абсолютно детерминированной системе между переменными существует обратная связь и присутствуют нелинейные компоненты, то ее поведение может становиться непредсказуемым (хаотичным) [16, 19].
Однако в течение длительного периода в биологии и социальных науках непредсказуемые изменения характеристик интерпретировались как стохастический «шум» или случайная экспериментальная ошибка. Но интерес биологов, психологов, социальных исследователей (всех, кого можно назвать «не-физиками») к использованию дифференциальных и разностных уравнений для описания популяционной, личностной динамики, социальных процессов, математическим исследованиям возможных паттернов поведения в этих областях, описываемых этими уравнениями в 70-ых годах 20-го века также привел к изменениям в трактовке непредсказуемости [18,10].
1.2. Принципы нелинейно-динамической теории для анализа временных рядов
Согласно теории нелинейных динамических систем, сложная система обладает свойствами, не присущими составляющим ее компонентам, поэтому поведение такой системы не может быть сведено к поведению отдельных ее частей [Wolfram, 2002]. Так, например, системные психологические конструкты высокого порядка: воля, саморегуляция, доступ к себе и т.п., - не могут быть разложены на более простые составляющие [23, 26].
Для построения моделей используются дифференциальные и разностные уравнения: первые - в предположении непрерывности процесса, вторые - в случае, когда процесс полагается дискретным. Один из наиболее популярных примеров первого типа - модель хищник-жертва (или Лотка-Вольтерра, см Митина 2002). Изначально использовалась для описания изменения численности особей рыб различного вида, живущих в одном водоеме. Однако эта модель оказалась продуктивной для описания психологических и социальных процессов: взаимодействия пар мать-ребенок в случаях невротических расстройств у матери, динамики мотивационной сферы (сосуществования мотивов базисного и более высокого уровней) [Митина, 2002], взаимодействия экономических систем стран разного уровня развития [Choi] и пр.
В то же время было показано, что многие динамические процессы в психологии на самых разных уровнях регулирования (эмоциональном, мотивационном, поведенческом, деятельностном) имеют определенный дискретный шаг изменения. В зависимости от природы процесса - такой единицей может быть год, день, даже секунда. Ситуация (состояние системы или любой ее части) в момент времени n зависит от состояния этой системы в предыдущие моменты времени. Уравнения, используемые в этом случае, называются разностными. Семейство простейших разностных уравнений имеет вид 
где 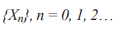 - последовательные состояния системы, F- функция от одной переменной.
- последовательные состояния системы, F- функция от одной переменной.
Проведенные в 70-х годах прошлого века исследования математических свойств этих отображений показали, что даже в случае самых простых функций Fдинамика, описываемая с использованием этой функции, может иметь очень сложную, даже непредсказуемую структуру [11, 28, 29, 30].
Выявленные свойства одномерных разностных уравнений и разнообразие моделей, которые можно построить с помощью этих уравнений с одной стороны, и математическая простота, с другой, приводят к их чрезвычайной популярности среди исследователей в самых разных областях науки (биологов, психологов, социальных исследователей, экономистов) [1,2, 21, 31].
Изучить поведение динамической системы - значит уметь сказать, что случится через достаточно длительный промежуток времени при заданных значениях управляющих параметров и начальных условиях, т.е. описать множество финальных состояний системы. Финальные множества - набор тех и только тех состояний, в которых система пребывает, начиная с определенного момента времени. Более строго:
Для функции 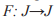 и любой точки
и любой точки 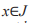 будем обозначать
будем обозначать
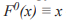 - тождественная функция,
- тождественная функция,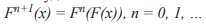
Введем следующее определение:
пpоявляется периодической точкой с периодом n если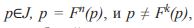 для
для 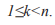 Множество всех точек
Множество всех точек 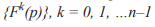 называется орбитой точки p.
называется орбитой точки p.
Финальное множество состоит из всех таких периодических точек и их орбит [15, 30, 38]. Придя в одну из точек финального множества (точнее в состояние, которому соответствует эта точка) система продолжает оставаться на ее орбите бесконечно долго при отсутствии внешних воздействий. Однако в зависимости от того, какова должна быть сила внешнего воздействия, способного вывести систему из состояния равновесия, различают равновесие неустойчивое - достаточно минимального внешнего воздействия, чтобы система это равновесное состояние покинула, и устойчивое - система подавляет небольшие флуктуации и остается в том же равновесном состоянии [7, 18, 38].
Периодическая точка 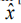 периодом 1 является фиксированной точкой (устойчивым состоянием). В этой ситуации выполняется условие:
периодом 1 является фиксированной точкой (устойчивым состоянием). В этой ситуации выполняется условие: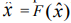
Поскольку изначально теория нелинейных динамических систем развивалась и вырабатывала свой понятийный аппарат исходя из нужд физики, очень многие определения наглядно могут быть проиллюстрированы известными примерами из школьного курса. Так, например, на рис. 1 изображены два шарика, находящиеся в состоянии равновесия. Однако если в первом случае (а) малейшее воздействие приводит к тому, что шарик скатывается с горки, то во втором случае (б) при не очень сильных воздействиях и достаточно глубокой лунке, шарик все равно будет скатываться на дно. Заметим, однако, что какова бы ни была глубина лунки, всегда можно толкнуть шарик так сильно, что он выскочит за ее пределы. Т.е. устойчивое равновесие очень часто оказывается устойчивым к внешним воздействиям до определенного предела.

а) Состояние неустойчивого равновесия б) Состояние устойчивого равновесия
Рис. 1. Шарик на поверхности равновесия
Стабильность системы и процесса определяется паттернами финального поведения или финальным множеством. Если состояние равновесия устойчиво, финальное множество называют аттрактором. В соответствии с количеством точек, входящих в финальное множество говорят об одноточечном аттракторе (финальное множество состоит из единственной точки), периодическом аттракторе (финальное множество состоит из конечного или счетного набора точек, представляющих совокупность орбит). Если множество точек в аттракторе - несчетно, такой аттрактор называется хаотическим или странным [8, 18, 38]. Это означает, что начиная с определенного момента времени, система достигает финального множества (аттрактора), каждый раз находится на одном из его элементов, однако принципиально невозможно сказать, где именно. Описать финальное множество - значит установить, является ли оно устойчивым (аттрактором) и сколько в нем элементов.
Пусть 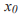 - периодическая точка с периодом n и множество
- периодическая точка с периодом n и множество 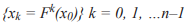 ее орбита. Если
ее орбита. Если

орбита является аттрактором. Если

орбита не стабильна [May].
Если существует единственная неподвижная точка (равновесие) то условие устойчивости приобретает вид

Таким образом, чтобы установить стабильным или нестабильным является финальное множество системы, достаточно вычислить производные функции во всех его точках и определить, какое из неравенств 2 или 3 выполняется.
Особый интерес при исследовании финального множества представляет характер его изменений в связи с изменениями параметров функции F. Если число точек в финальном множестве остается прежним, а изменяются лишь их значения, то говорят о количественных изменениях. Более глубокие (качественные) изменения затрагивают структуру финального множества: число точек может увеличиться или уменьшиться, из конечного превратиться в бесконечное или наоборот. Параметры функции F, изменения которых могут привести к таким глубоким изменениям финального множества, называются управляющими параметрами. Значения управляющих параметров, при достижении которых происходит структурное изменение финального множества, называется точками бифуркации. График, отражающий зависимость значений финального множества от значений управляющего параметра, называется бифуркационной диаграммой. Построить такой график для каждого управляющего параметра сложно и требуется глубокая аналитическая и вычислительная работы. Эти трудности и объясняют тот факт, что для большинства функций построены только качественные бифуркационные диаграммы (схемы зависимостей значений финального множества от значений управляющего параметра), а не точные количественные графики. А ведь только на основе последнего возможен полноценный анализ паттернов финального поведения системы.
Наиболее известным, хорошо изученным примером одномерного разностного уравнения является логистическое отображение, в стандартном виде имеющее вид:
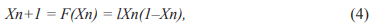
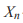 -сомножитель, отражающий возможную позитивную обратную связь;
-сомножитель, отражающий возможную позитивную обратную связь;
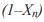 - сомножитель, отражающий возможную негативную обратную связь;
- сомножитель, отражающий возможную негативную обратную связь;
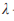 - управляющий параметр;
- управляющий параметр;
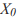 - начальное значение.
- начальное значение.
1.3. Свойства логистического отображения
Логистическое отображение - простейшая модель в теории самоорганизационных динамических систем, учитывающая, что влияние предыдущего состояния (характеризуемого величиной какой-то характеристики, параметра) на последующее является амбивалентным (с одной стороны стимулирующим, с другой - подавляющим). В результате мы имеем возможность отказаться от однонаправленной логики классической методологии и исследовать нелинейное двунаправленное влияние.
Функция полностью изучена, ее бифуркационная диаграмма в точности построена. Величина измеряемой динамической характеристики 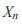 в момент n (номер измерения, шаг и т.п.) определяется относительно к максимально возможной величине этой характеристики и лежит в диапазоне от 0 до 1. Параметр
в момент n (номер измерения, шаг и т.п.) определяется относительно к максимально возможной величине этой характеристики и лежит в диапазоне от 0 до 1. Параметр 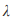 также лежит в ограниченном диапазоне от 0 до 4. Это ограничение необходимо для того, чтобы уравнение всегда имело смысл. Зная
также лежит в ограниченном диапазоне от 0 до 4. Это ограничение необходимо для того, чтобы уравнение всегда имело смысл. Зная 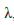 , для любого начального условия
, для любого начального условия 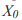 пользуясь формулой (4), можно вычислить последовательность значений X1, X2, X3... Например для
пользуясь формулой (4), можно вычислить последовательность значений X1, X2, X3... Например для 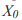 = 0.62 и
= 0.62 и 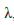 = 3.1, вычисляемая последовательность будет равна 0.620000, 0.730360, 0.610496, 0.737151, 0.600654, 0.743593.0.764568, 0.558015, 0.764568, 0.558014. Мы видим, что с определенного момента два числа начинают сменять одно другое и это происходит сколь угодно долго. Таким образом, можно говорить о наличии двухточечного аттрактора.
= 3.1, вычисляемая последовательность будет равна 0.620000, 0.730360, 0.610496, 0.737151, 0.600654, 0.743593.0.764568, 0.558015, 0.764568, 0.558014. Мы видим, что с определенного момента два числа начинают сменять одно другое и это происходит сколь угодно долго. Таким образом, можно говорить о наличии двухточечного аттрактора.
Другой способ определения финального множества - графический. Он представлен на рис. 2. Верхние графики на каждом из рисунков а-в представляют логистическое отображение в фазовом пространстве в координатах 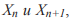 , отражают зависимость последующего состояния от предыдущего. Для того чтобы найти финальное множество для фиксированной начальной точки помимо параболы на графике нужно провести биссектрису первого координатного угла, отметить начальную точку
, отражают зависимость последующего состояния от предыдущего. Для того чтобы найти финальное множество для фиксированной начальной точки помимо параболы на графике нужно провести биссектрису первого координатного угла, отметить начальную точку 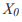 на оси абсцисс и последовательно выполнять следующие построения:
на оси абсцисс и последовательно выполнять следующие построения:
- из точки 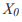 восстановить перпендикуляр до пересечения с параболой. Ордината точки пересечения равна
восстановить перпендикуляр до пересечения с параболой. Ордината точки пересечения равна 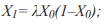
- из точки пересечения провести прямую, параллельную оси абсцисс до пересечения с биссектрисой. Абсцисса точки пересечения равна 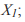
- из точки пересечения провести прямую, параллельную оси ординат до пересечения с параболой. Ордината точки пересечения равна 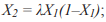
- из точки пересечения провести прямую, параллельную оси абсцисс до пересечения с биссектрисой. Абсцисса точки пересечения равн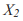 а и т.д.
а и т.д.
В результате последовательность либо сходится к одной точке (рис. 2а), либо к конечной ломаной линии (на рис. 2б это квадрат), либо этот процесс никогда не заканчивается и ломаная линия последовательно заполняет все пространство (рис. 2в). Нижние графики на рисунках - временная развертка. По оси абсцисс откладывается время, а по оси ординат - состояния системы в каждый момент времени. Если линия становится параллельной оси абсцисс - значит процесс достиг стационарной точки. На рис. 2а эта точка достигается, на рис. 2б процесс заканчивается на двухточечной орбите, на рис. 2в процесс не выходит на орбиту вообще. При этом не имеет значения, начиная с какой точки X0 построения выполняются. На рисунке 2 в каждом случае представлено две последовательности, начинающиеся в разных точках, а финальные множества в каждом случае оказываются одинаковыми.
Таким образом логистическое отображение задает детерминированную последовательность, но при разных значениях 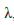 структура финального множества меняется существенным образом (и зависит исключительно от величины l).
структура финального множества меняется существенным образом (и зависит исключительно от величины l).

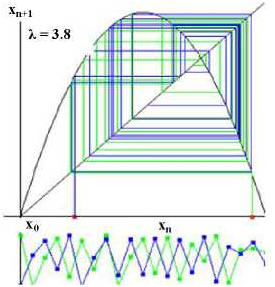
в) Хаотический аттрактор
Рис. 2. Паттерны сходимости логистических последовательностей при различных управляющих параметрах.
Однако можно подобных вычислений или построений не проводить, а установить устойчивость аналитическим путем, исследовав производную в стационарных точках. Эти точки являются решениями уравнения

Их два:

При 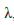 < 1,второе решение лежит вне установленной ранее области [0; Лебедев, 2005], а потому не имеет смысла. Таким образом, при
< 1,второе решение лежит вне установленной ранее области [0; Лебедев, 2005], а потому не имеет смысла. Таким образом, при 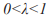 существует только одна точка равновесия, а при
существует только одна точка равновесия, а при 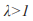 равновесных точек две. Геометрически это означает, что в первом случае на указанном интервале парабола пресекает биссектрису гла только в точке 0.
равновесных точек две. Геометрически это означает, что в первом случае на указанном интервале парабола пресекает биссектрису гла только в точке 0.
Согласно (2 ) финальное множество является одноточечным аттрактором, когда производная функции, задающей отображение по модулю не превосходит 1. Поэтому

Соотственно

Таким образом только при 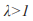 логистическое отображение имеет ненулевую устойчивую неподвижную точку.
логистическое отображение имеет ненулевую устойчивую неподвижную точку.
На рис. 3 представлена бифуркационная диаграмма логистического отображения. Ось абсцисс соответствует управляющему параметру 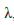 , а по оси ординат откладываются значения чек финального множества во временной серии, порожденной логистическим уравнением приданном 2. На рис. За представлен весь график целиком.
, а по оси ординат откладываются значения чек финального множества во временной серии, порожденной логистическим уравнением приданном 2. На рис. За представлен весь график целиком.
После того как 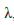 преодолеет рубеж равный 3 число устойчивых финальных точек начинает последовательно удваиваться. При
преодолеет рубеж равный 3 число устойчивых финальных точек начинает последовательно удваиваться. При 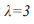 у финального множества возникает вторая точка, затем их становится 4, 8 ... и т.д. На рис. Зб этот процесс представлен более наглядно. При этом выполняется следующее соотношение
у финального множества возникает вторая точка, затем их становится 4, 8 ... и т.д. На рис. Зб этот процесс представлен более наглядно. При этом выполняется следующее соотношение
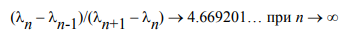
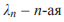 бифуркационная точка. Это соотношение было установлено Л. Фейгенбаумом [Feigenbaurn], (см.также [З5]).
бифуркационная точка. Это соотношение было установлено Л. Фейгенбаумом [Feigenbaurn], (см.также [З5]).
Процесс удвоения периода происходит до тех пор пока лямбда не достигает значения равного 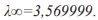 Именно при этом значении управляющего параметра финальное множество становится бесконечным (странным хаотическим аттрактором). Т.е. при
Именно при этом значении управляющего параметра финальное множество становится бесконечным (странным хаотическим аттрактором). Т.е. при 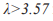 невозможно сказать, где находится система в каждый конкретный момент времени.
невозможно сказать, где находится система в каждый конкретный момент времени.
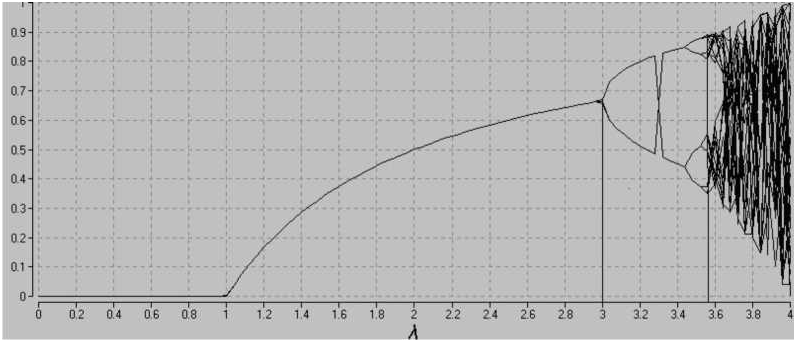
a) Общий вид
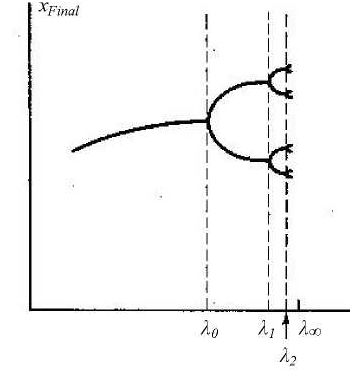
б) Схематический фрагмент диаграммы
Рис. 3. Бифуркационная диаграмма логистического отображения
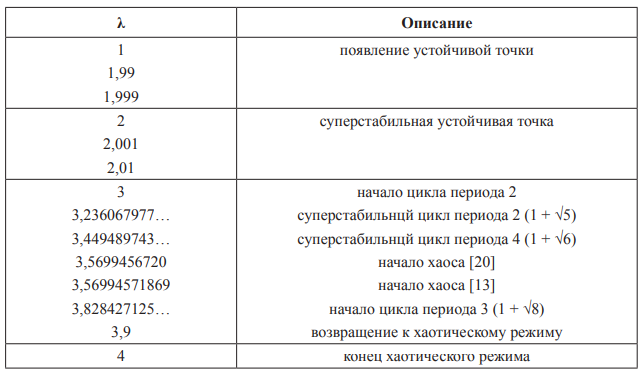
В дополнении к бифуркационной диаграмме в таблице 1 более точно указываются наиболее важные с точек зрения изменения структуры финального множества, а значит качественного характера временного ряда значения 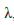 .
.
Таблица 1. Описание наиболее важных значений управляющего параметра 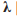 [14, 28]
[14, 28]
Несмотря на простоту логистического отображения оно позволяет моделировать очень сложные процессы. Изначально эта модель использовалась для описания популяционной динамики, в дальнейшем нашла широкое применение в экономике, политологии и других социальных науках. Однако в течение многих лет модели, для описания процессов создавались на основе теоретических идей, исходя из которых устанавливался закон связи значений динамической переменной, полученных в различные моменты времени. Например, заключения, что численность популяции в момент времени n+1 есть функция от численности популяции в момент времени n было сделано исследователями на основе теоретических рассуждений о законах существования популяции [17, 9]. В настоящее время можно говорить о более общем использовании таких функций не только в случае, когда взаимосвязи между измерениями, сделанными в последовательные моменты времени, выводятся теоретически, но и когда модель строится на основании эмпирических данных, полученных в экспериментальном лонгитюдном исследовании, а затем экстраполируется на весь временной период и на всю популяцию в целом [2, 3, 36].В психологии эта функция используется для исследования мотивации [25, 26], динамики эмоциональной сферы [24, 33], в экономике [Jakimowicz, 2010], в биологии для изучения динамики популяций, на клеточном уровне для анализа процессов восстановления клеток после стрессового воздействия.
1.4. Приведение квадратичной параболы общего вида к стандартному виду логистического отображения
В ситуации когда модель логистического отображения используется для описания и анализа реального эмпирического временного ряда, задачей первого этапа является выбор функции в наибольшей степени согласованной с эмпирическими данными, с тем, чтобы потом уже полученную функцию рассматривать в качестве графика изучаемого процесса, выводы о его свойств х дела ь на основе свойств ппрок имитирующей функции.
Заметим, что использование квадратичной функции общего вида

содержащей три варьируемых параметра в сравнении с стандартным логистическим отображением с единственным параметром, позволяет подобрать согласуются с экспериментальным данными функцию из более широкого класса, что дает существенно лучший показатель согласованности. Но квадратичную функцию общего вида всегда можно привести к виду логистического отображеия используя линейное преобразование

не меняющее свойства финального множества, т.к. финальное множество объясняется свойствами производной функции, которая в свою очередь никак не зависят от линейных преобразований. В этой новой системе координат парабола общего вида имеет вид

Т.к. линейное преобразование не меняет динамических свойств (стабильная система остается стабильной, нестабильная - нестабильной, число финальных точек также не изменяется) мы можем изучать квадратичную параболу в новой координатной системе, записанной в виде (10) и эти свойства будут теми же, что и у параболы написанной в (4). Это значит, что в случае 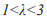 будет только одна стабильная точка , в интервале от 3 до 3.57 происходит удвоение периода и при
будет только одна стабильная точка , в интервале от 3 до 3.57 происходит удвоение периода и при 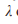 от 3.57 до 4 финальное множество становится хаотическим аттрактором. Коэффициенты линейного преобразования u и v, а также управляющий параметр
от 3.57 до 4 финальное множество становится хаотическим аттрактором. Коэффициенты линейного преобразования u и v, а также управляющий параметр 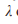 для стандартного вида однозначно вычисляются на основе коэффициентов параболы общего вида a, b,c согласно уравнению (10).
для стандартного вида однозначно вычисляются на основе коэффициентов параболы общего вида a, b,c согласно уравнению (10).
Проведем замену в первой и левой части уравнения 10 на основании преобразования (9), имеем
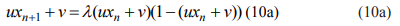
Преобразование правой части уравнения(10а) дает
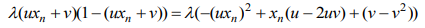
Подстановка этого выражения в (10а) и дальнейшее преобразование дают:
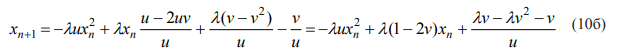
Уравнения 4 и10б должны быть идентичны. Это значит, что коэффициенты в каждом члене должны быть одинаковы. Следуя этому правилу, имеем:
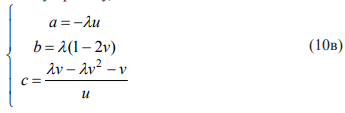
Полагая a, b, с известными, мы можем выразить параметры линейного преобразования (9) u и v, а также управляющий параметр λ, задающий стандартную форму логистического отображения в новой системе координат (9)).
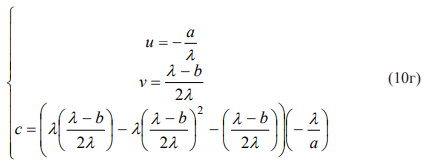
Преобразование третьего уравнения из системы дает:

После вычислений имеем:
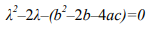
таким образом, можно выразить 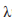 через a, b, c
через a, b, c
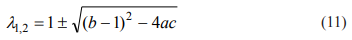
Как уже было сказано, структурные свойства стабильности временного ряда не изменяются после линейных преобразований. Это утверждение следует из того что свойства стабильности определяются значениями первой производной. (См. 2, 3).
Действительно
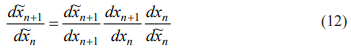
И для любого линейного преобразования (9)

Поэтому

Поэтому, чтобы описать свойства квадратичного отображения общего вида, достаточно с помощью формулы (11) вычислить соответствующую 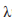 , и, если одна из них лежит в диапазоне от 0 до 4, то динамические свойства отображения определяются в соответствии с тем, какому подинтервалу на участке от 0 до 4
, и, если одна из них лежит в диапазоне от 0 до 4, то динамические свойства отображения определяются в соответствии с тем, какому подинтервалу на участке от 0 до 4 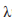 принадлежит: меньше 1, от 1 до 3, от 3 до 3.57 и т.д). Заметим, что в сумме два корня, определяемы в соответствии с уравнние (11) равны 2:
принадлежит: меньше 1, от 1 до 3, от 3 до 3.57 и т.д). Заметим, что в сумме два корня, определяемы в соответствии с уравнние (11) равны 2:
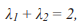
поэтому
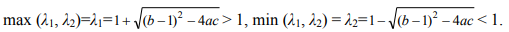
При этом если один из корней (любой) является управлющим параметром (выражаемым через коэффициенты квадратичной параболы общего вида), то второй - это значение производной в ненулевой равновесой точке первоначальной системе к ординат (также выраженной через коэффициенты параболы). Для устойчивости равновесной точки необходимо, чтобы производная в ней п абсолютной величине была меньше 1. Поскольку 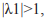 то условие устойчивости ра весия вып лняется в случае
то условие устойчивости ра весия вып лняется в случае 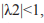 что равносильно тому, что
что равносильно тому, что 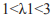 (условию устойчивости по управляющему параметру).
(условию устойчивости по управляющему параметру).
Т.о. для квадратичной параболы общего вида (8), при условии существования вещественных реший (11), характер финального множества определяется исходя из правил логистического отображения с управляющим параметром равным

Отсутствие решений геометрически означает отсутствие пересечений параболы, определяемой уравнением (8), и биссектрисы первого координатного угла.
1.5. Выбор модельной функции
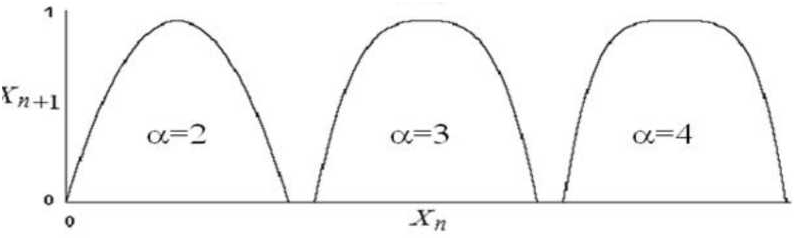
При наличии теоретического обоснования ограниченности анализируемых показателей (т.е. того, что показатели не могут быть сколь угодно велики, а обязательно лежат в каком-то пусть и большом диапазоне), функция, задающая отображение, после периода возрастания должна обязательно убывать. Простейшие функции такого типа - дифференцируемые ограниченные функции с одним максимумом (унимодальные). К ним относится не только логистическое отображение, но и другие семейства функций, которые также могли бы быть использованы для описания подобных процессов. Среди таких семейств: синусоидальное отображение 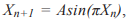 общее симметричное отображение
общее симметричное отображение 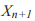
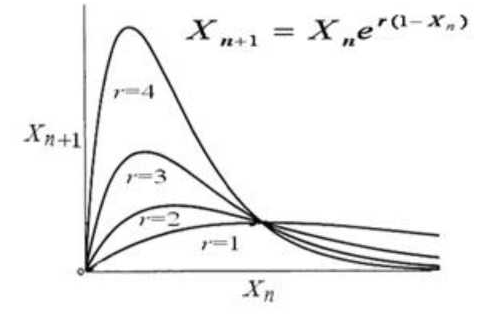
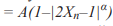 (рис. 4а), экспоненциальное отображение
(рис. 4а), экспоненциальное отображение 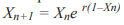 (рис. 4б). Последнее семейство реализует несимметричные отображения. Заметим, что все несимметричные функции, принципиально отличающиеся от симметричных, определены на бесконечном интервале (полуоси) (в противном случае можно выполнить определенную трансформацию, с одной стороны не меняющую свойства функции, а с другой - симметризующую ее). Однако в рассматриваемом случае мы условились, что интервал определенности функции должен быть ограничен, поэтому не будем рассматривать функции, представленные на рис. 4б.
(рис. 4б). Последнее семейство реализует несимметричные отображения. Заметим, что все несимметричные функции, принципиально отличающиеся от симметричных, определены на бесконечном интервале (полуоси) (в противном случае можно выполнить определенную трансформацию, с одной стороны не меняющую свойства функции, а с другой - симметризующую ее). Однако в рассматриваемом случае мы условились, что интервал определенности функции должен быть ограничен, поэтому не будем рассматривать функции, представленные на рис. 4б.
Все симметричные функции с высоким уровнем значимости апроксимируются квадратичными параболами. Для доказательства этого факта были специально сгенерированы большие массивы пар чисел на основе всевозможных унимодальных из различных семейств, а затем на этих парах была проведена аппроксимация квадратичными параболами. Во всех случаях показатель согласованности данных 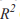 был не ниже 0.9.
был не ниже 0.9.
![]()
а) Общее симметричное отображение, а=2 дает логистическое отображение
б) Экспоненциальное отображение
Рис. 4. Примеры унимодальных функций
Таким образом квадратичная парабола общего вида может с большой степенью точности заменить все остальные унимодальные отображения, определенные на ограниченном интервале. В силу данной эквивалентности, с одной стороны, а так же возможности представления в виде стандартного логистического вида (4), наиболее простого и лучше всего изученного, первоначальная аппроксимация экспериментальных данных с помощью квадратичной параболы (с посл дующим линейным преобразование системы координат, так что квадратичная функция приобретает вид стандартного логистического отображения) является наиболее целесообразным.
1.6. Процедура построения логистического уравнения
Процедура построения логистического уравнения для набора данных 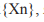 являющегося временным рядом из N наблюдений, выглядит следующим образом (см. также схему алгоритма, представленнуюнарис. 5):
являющегося временным рядом из N наблюдений, выглядит следующим образом (см. также схему алгоритма, представленнуюнарис. 5):
- Формируются две переменные, содержащие N-1 наблюдений.
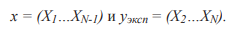
2. Выполняется регрессия уэксп на x с использованием квадратичной формулы общего вида. Т.е. зависимая переменная уэксп апроксимируется модельной переменной
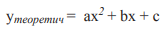
3. В случае хорошей согласованности модели с экспериментальными данными (уровень значимости нулевой гипотезы низкий 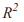 - высокий) - данная регрессионная модель принимается и на основе полученной квадратичной функции по формуле 12 вычисляется
- высокий) - данная регрессионная модель принимается и на основе полученной квадратичной функции по формуле 12 вычисляется 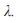 Это необходимое условие для построения модели.
Это необходимое условие для построения модели.
4. Если решение в п.3 существует, то существуют точки равновесия.
5. Еще одно условие, которое должно выполняться связано с пределами, в которых может лежать полученное 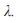 Если
Если 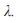 принадлежит интервалу от 0 до 4, будем говорить о том, что процесс можно представить логистическим отображением. В этом случае отображение и представляемый им процесс можно исследовать.
принадлежит интервалу от 0 до 4, будем говорить о том, что процесс можно представить логистическим отображением. В этом случае отображение и представляемый им процесс можно исследовать.
6. Если 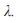 лежит в диапазоне от 1 до 3, будем говорить о стабильности процесса.
лежит в диапазоне от 1 до 3, будем говорить о стабильности процесса.
7. При 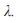 , лежащем в диапазоне от 3 до 4, характер процесса, структура финального множества определяется в соответствии с бифуркационной диаграммой (рис. 3, таблица 1), имеет место нестабильность.
, лежащем в диапазоне от 3 до 4, характер процесса, структура финального множества определяется в соответствии с бифуркационной диаграммой (рис. 3, таблица 1), имеет место нестабильность.
Требуемый объем данных (т.е. количество измерений во временном ряду) определяется статистическими требованиями выполнения регрессии. Чем это число больше, тем выше надежность вычисляемых показателей.
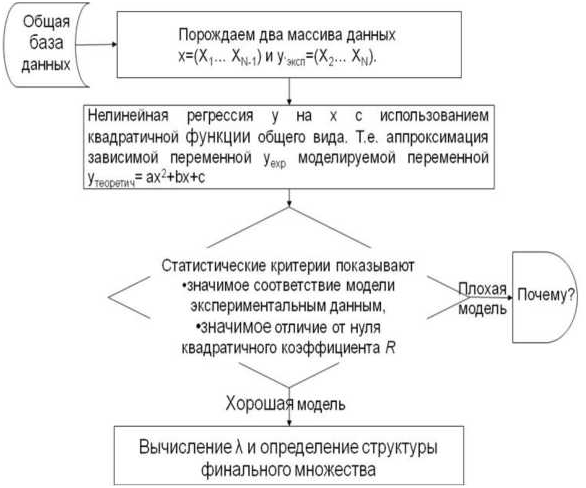
Рис. 5. Схема алгоритма построение модели логистического отображения для эмпирического исследования
1.7. Практическая апробация предлагаемого алгоритма
Практическая апробация предлагаемого алгоритма была выполнена для анализа данных, полученных в (1) биогенетическом и (2) психологическом исследовании.
1. В первом случае проводился анализ динамики экспрессии генов (выражаемой в величине их концентрации в растворе) растительных клеток после «стрессового» воздействия [Sprott.J.C]. Предполагалось, что после воздействия на клетки не оказывают воздействие никакие возмущающие факторы и идет самовосстановление к первоначальному состоянию по закону (4). (Более подробное обоснование правомерности данной модели см. в указанной работе). Для сравнения анализировались гены изолированных клеток и клеток, составляющих целое растение. Было выполнено 9 замеров с момента стрессового воздействия (дополнительного воздействия серой). На ряду с двумя экспериментальными группами аналогичные замеры проводились на контрольных группах (изолированных клеток и целостных растений), в которых не было стрессового воздействия. В данной ситуации количество замеров мало, однако это компенсировалось объемом выборки - было проанализированы показатели по 22.810 генам в каждой из 4-х групп.
Результаты анализа показали, что поведение изолированных клеток в ситуации стресса становится хаотичным, идущим в «разнос», а клетки целостных растений в этом случае демонстрируют большую устойчивость и способность к конструктивной адаптивной модификации. Можно сделать вывод что более высокие системные свойства целостного растения позволяют его клеткам легче адаптироваться, либо сохраняя свою идентичность, либо, допуская самые малые, наиболее выгодные с точки зрения преодоления стресса, изменения.
Нам кажется обоснованным провести аналогию здесь с социальным коллективом. Действительно сплоченный коллектив гораздо легче (по сравнению с отдельными ничем несвязанными между собой индивидами) переносит ситуацию стресса, оптимально модифицирует свое функционирование. Пословицы «На миру и смерть красна», «Один в поле не воин» достаточно ярко иллюстрирует эту идею.
2. Второе исследование изучало динамику аффективных состояний.46 человек (39 женщин, 9 мужчин) - студенты в течение 28 дней заполняли дневники о своих позитивных и негативных эмоциях, далее для каждой из этих последовательностей вычислялись регрессионная квадратичная кривая общего вида, а затем управляющий параметр стандартной формы логистического отображения. Кроме того респонденты один раз заполняли большую батарею личностных опросников, связанных со стилевыми, личностными особенностями, мотивационной структурой [24, 32, 33]. В дальнейшем проводился анализ детерминаций полученных значений 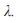 для каждого типа аффекта индивидными характеристиками. Было установлено, что все
для каждого типа аффекта индивидными характеристиками. Было установлено, что все 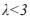 (для всех испытуемых и всех видов аффектов). Динамика для всех состояний при отсутствии вынуждающих внешних воздействий у психически здоровых людей приходит к одной устойчивой точке. Т.е. у человека в норме невозможны постоянные колебания между какими-то двумя показателями на эмоциональной шкале. Кроме того дисперсионный анализ не выявил значимых различий в распределении
(для всех испытуемых и всех видов аффектов). Динамика для всех состояний при отсутствии вынуждающих внешних воздействий у психически здоровых людей приходит к одной устойчивой точке. Т.е. у человека в норме невозможны постоянные колебания между какими-то двумя показателями на эмоциональной шкале. Кроме того дисперсионный анализ не выявил значимых различий в распределении 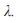 , вычисленных для разных эмоциональных шкал. Можно говорить, что это внутренняя индивидная характеристика, связанная с достижением наиболее приемлемого для индивида эмоционального уровня. Это есть финальная устойчивая точка, к которой сходится динамический процесс (она равна
, вычисленных для разных эмоциональных шкал. Можно говорить, что это внутренняя индивидная характеристика, связанная с достижением наиболее приемлемого для индивида эмоционального уровня. Это есть финальная устойчивая точка, к которой сходится динамический процесс (она равна 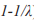 ) при отсутствии внешних вынуждающих воздействий. Конечно, следует иметь в виду, что данная величина в большинстве случаев реально недостижима, ибо полностью изолировать человека от внешних воздействий практически невозможно. Тем не менее, возможность ее учета при построении личностного портрета, практической психотерапевтической и консультационной работы нам представляется полезным и эффективным.
) при отсутствии внешних вынуждающих воздействий. Конечно, следует иметь в виду, что данная величина в большинстве случаев реально недостижима, ибо полностью изолировать человека от внешних воздействий практически невозможно. Тем не менее, возможность ее учета при построении личностного портрета, практической психотерапевтической и консультационной работы нам представляется полезным и эффективным.