Гарантирующее оценивание параметров одномерной модели движения по вероятностному критерию при наличии унимодальных помех

Рассматривается задача линейного параметрического оценивания в одномерной модели движения материальной точки при наличии измерительных ошибок с неопределенным симметричным унимодальным распределением, но известными ковариациями и дисперсиями. Установлены гарантированные границы для вероятности превышения ошибкой оценивания заданного порога с учетом априорных ограничений на начальное положение и скорость. Проведено сравнение качества ридж-оценок для нескольких классов распределений помех.

Рассматривается задача линейного параметрического оценивания в одномерной модели движения материальной точки при наличии измерительных ошибок с неопределенным симметричным унимодальным распределением, но известными ковариациями и дисперсиями. Установлены гарантированные границы для вероятности превышения ошибкой оценивания заданного порога с учетом априорных ограничений на начальное положение и скорость. Проведено сравнение качества ридж-оценок для нескольких классов распределений помех.

1.    ВВЕДЕНИЕ

Различные постановки задач параметрического оценивания остаются предметом изучения многих теоретических исследований [Simon, 2006]. Практическое применение оценок требует более осторожных выводов об их точности и надежности особенно в ситуации небольшого числа наблюдений и неопределенности распределения ошибок [Maryak, 2004]. Один из подходов к повышению робастности статистических решений состоит в определении наихудших границ их качества при допущении всевозможных распределений с ограниченными или фиксиро­
ванными моментными характеристиками второго порядка [Delage, 2010]. Однако такой класс распределений приводит к достаточно пессимистическим выводам о вероятностных характеристиках точности робастных оценок. Более реалистичным выглядит использование дополнительной непараметрической информации о распределении, которое формулируется в виде естественного требования унимодальности [Dharmadhikari, 1988]. Если качество оценок описывается вероятностью выхода ошибки за определенные пределы [Панков, 2007], то гарантированные границы этого вероятностного

критерия качества можно получить на основе недавно разработанных обобщений неравенства Гаусса [6,7].

В настоящей работе рассматривается задача оценивания будущего положения объекта, который движется равномерно и прямолинейно, а его текущее положение наблюдается с учетом измерительных помех, имеющих неопределенное симметричное унимодальное распределение, но известную ковариационную матрицу. Описанная задача решается на основе гарантирующего подхода, который позволяет определить верхнюю границу вероятности превышения заданного порога ошибки с учетом априорных ограничений на начальное положение объекта и его скорость. Чтобы учесть априорную информацию о неизвестных параметров, вместо оценок метода наименьших квадратов (МНК) используются их регуляризо­ванные версии — так называемые ридж-оценки [Демиденко, 1981]. Проводится сравнительный анализ нескольких вариантов ридж-оценок при наличии разного уровня информированности о распределении помех.

2.    ОПИСАНИЕ МОДЕЛИ

3.     ПОСТАНОВКА ЗАДАЧИ

4.     ОЦЕНКИ И ИХ ХАРАКТЕРИСТИК

5.     ВЕРОЯТНОСТНЫЙ КРИТЕРИЙ

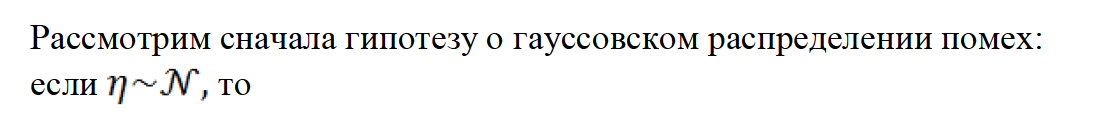
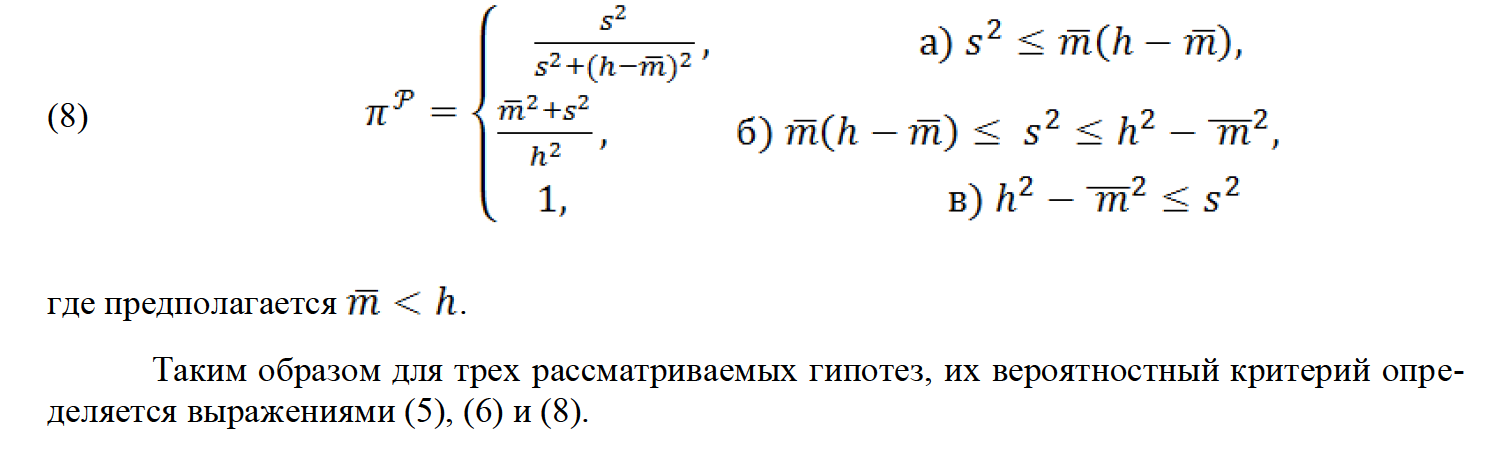
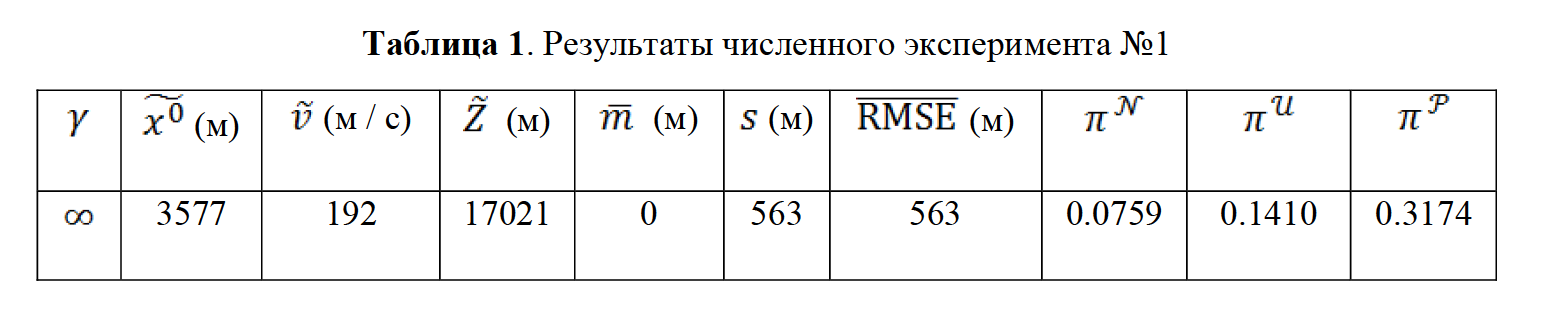
6. ЧИСЛЕННЫЙ ЭКСПЕРИМЕНТ

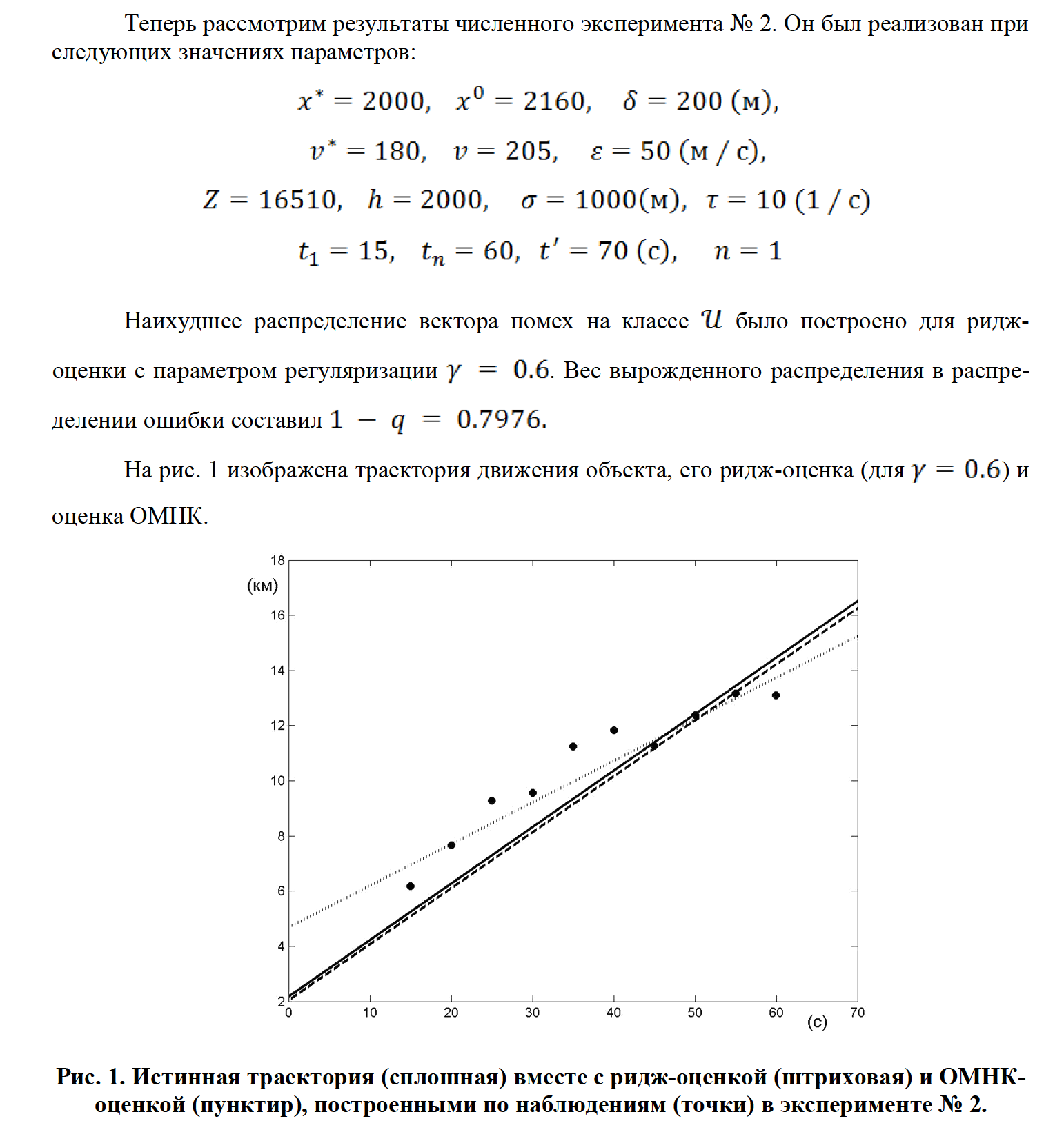
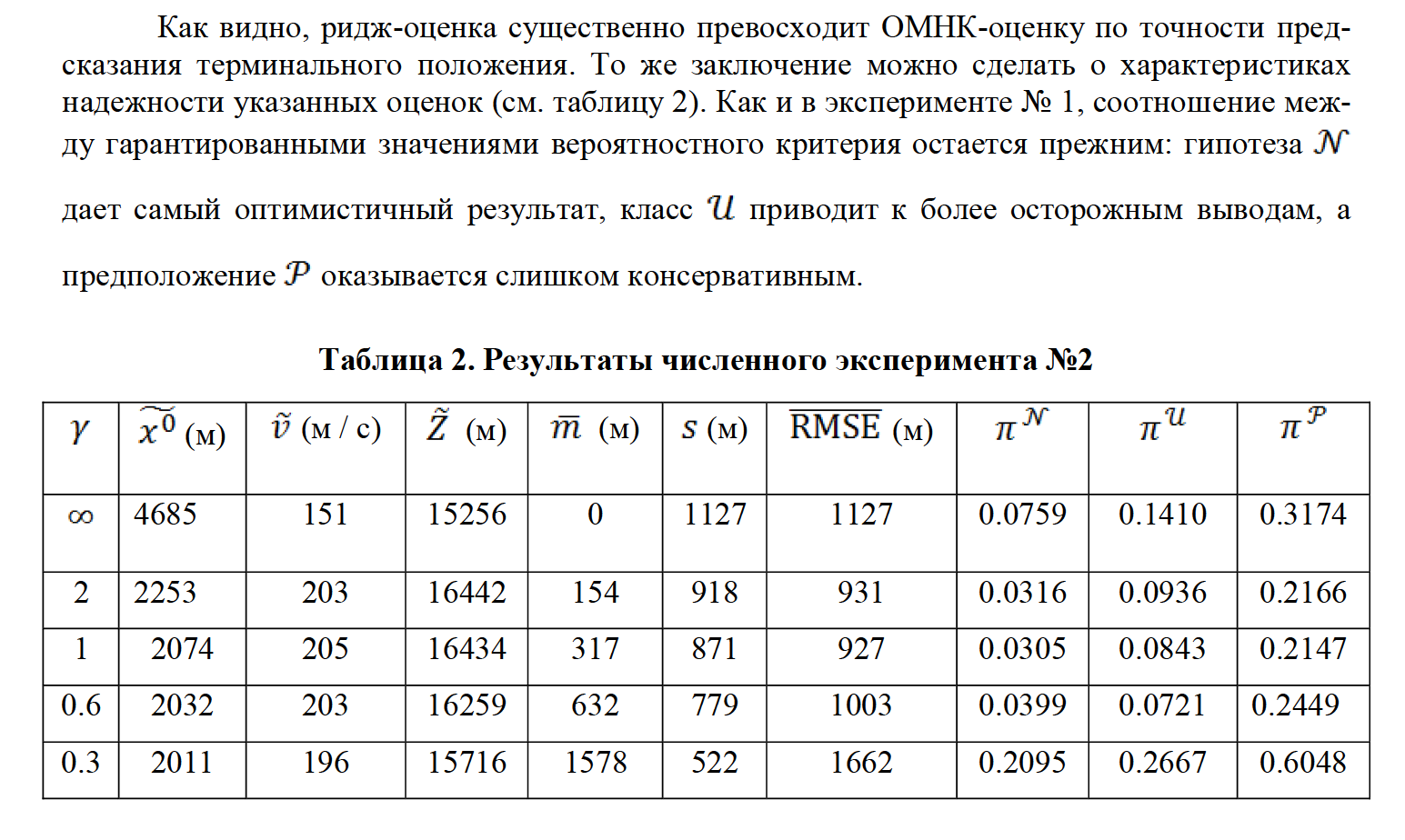
В заключение необходимо отметить, что коэффициенты ридж-оценки можно подобрать из условия минимума соответствующей вероятностной границы. Однако изучение данной задачи оптимизации выходит за рамки настоящей работы.

1. Simon D. Optimal State Estimation. Kalman, H-infinity, and Nonlinear Approaches. Wiley, 2006.
2. Maryak J.L., Spall J.C., Heydon B.D. Use of the Kalman filter for inference in state-space models with unknown noise distributions // IEEE Trans. Automat. Control. 2004. V. 49. P. 87-90.
3. Delage E., Ye Y. Distributionally robust optimization under moment uncertainty with application to data-driven problems // Operations Research. 2010. V. 58. P. 595-612.
4. Dharmadhikari S., Joag-Dev K. Unimodality, Convexity, and Applications. San Diego: Academic, 1988.
5. Панков А.Р., Семенихин К.В. О минимаксном оценивании по вероятностному критерию // Автоматика и телемеханика. 2007. № 3. С. 66-82.
6. Van Parys B.P.G., Goulart P.J., Kuhn D. Generalized Gauss inequalities via semidefinite programming // Math. Program. 2016. V. 156. P. 271-302.
7. Семенихин К.В. Двусторонняя вероятностная граница для сим етричной унимодальной случайной величины // Автоматика и телемеханика. 2019. №3. В печати.
8. Демиденко Е.З. Линейная и нелинейная регрессии. М.: Финансы и статистика, 1981.
9. Карлин С., Стадден В. Чебышевские системы и их применение в анализе и статистике. — М.: Наука, 1976.