Численный алгоритм поиска субоптимального управления дискретной стохастической системой с вероятностным критерием

Рассматривается численный алгоритм для поиска субоптимального управления для систем, заданных разностными уравнениями. С использованием численного метода удается найти изобеллы уровня 1 и 0, нахождение которых позволяет найти субоптимальное управление, не решая систему, в которой присутствует функция Беллмана, вычисление которой затруднительно. С использованием описанной численной процедуры решается пример, полученный результат сравнивается с аналитически найденым оптимальным управлением.

Рассматривается численный алгоритм для поиска субоптимального управления для систем, заданных разностными уравнениями. С использованием численного метода удается найти изобеллы уровня 1 и 0, нахождение которых позволяет найти субоптимальное управление, не решая систему, в которой присутствует функция Беллмана, вычисление которой затруднительно. С использованием описанной численной процедуры решается пример, полученный результат сравнивается с аналитически найденым оптимальным управлением.

1.  ВВЕДЕНИЕ

Задачи оптимального управления по вероятностным критериям качества составляют предмет изучения специального раздела теории стохастического оптимального управления. Основным алгоритмом решения данного типа задач является метод динамического программирования (МДП). Использование данного метода сопряжено с сложностью получения аналитического решения. Это подтверждается тем, что для достаточно простых систем получаемые решения имеют сложную структуру и их вычисление затруднительно, например, в работах [1, 2].

В данной статье предложен численный алгоритм для поиска субоптимального управления для задач с вероятностным точностным функционалом, который позволяет получать решение без вычисления функции Беллмана.

2.  ОБЩАЯ ПОСТАНОВКА ЗАДАЧИ

3.       ОПРЕДЕЛЕНИЕ ИЗОБЕЛЛ И ТЕОРЕМА О ДВУХСТОРОННЕЙ ОЦЕНКЕ ФУНКЦИИ БЕЛЛМАНА

4.     ЧИСЛЕННЫЙ МЕТОД РЕШЕНИЯ ЗАДАЧ СТОХАСТИЧЕСКОГО ОПТИМАЛЬНОГО УПРАВЛЕНИЯ ДИСКРЕТНЫМИ СИСТЕМАМИ ПО ВЕРОЯТНОСТНОМУ КРИТЕРИЮ

5. ПРИМЕР

Теория синтеза оптимального управления используется для решения задач из аэрокосмической отрасли, например, задача импульсной коррекции траектории космического аппарата (КА) на геостационарной орбите с помощью корректирующей установки малой тяги. Отклонение КА возникает из-за внешних возмущений и неопределенных факторов, возникающих из-за погрешности и ошибок в вычисление координат и различных параметров системы.

Проверим сформулированный алгоритм на подобной упрощенной модели и сравним с известным оптимальным управлением.

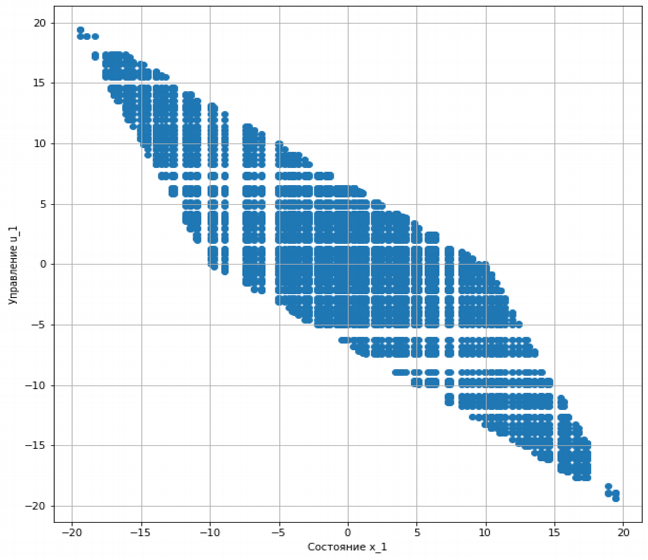
Рис 1. Множество U1I (x1)

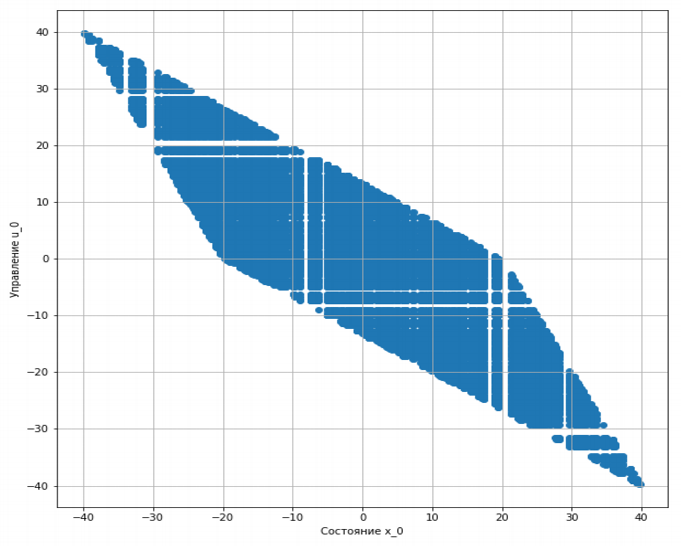
Рис 2. Множество U0I (x0)

1. Азанов В.М. Оптимальное управление линейной дискретной системой по критерию вероятности // Автоматика и Телемеханика. 2014. №10. С. 39–51.
2. Азанов В.М., Кан Ю.С. Однопараметрическая задача оптимальной коррекции траектории летательного аппарата по критерию вероятности // Изв. РАН Теория и Системы Управления. 2016. №2. С. 115-128.
3. Азанов В.М. Алгоритмы динамического программирования решения задач оптимального управления дискретной стохастической системой с терминальным вероятностным критерием // Диссертация на соискание учёной степени кандидата физико-математических наук. 2018.
4. Азанов В.М., Кан Ю.С. Синтез оптимальных стратегий в задачах управления дискретными системами по вероятностному критерию // Автоматика и Телемеханика, 2017, № 6, 57–83.
5. Азанов В.М., Кан Ю.С. Двухсторонняя оценка функции Беллмана в задачах стохастического оптимального управления дискретными системами по вероятностному критерию качества // Автоматика и Телемеханика, 2018, № 2, C. 3–18.
6. Кан Ю.С., Кибзун А.И. Задачи стохастического программирования с вероятностными критериями, Физматлит, М., 2009.
7. Кибзун А.И., Игнатов А.Н. Сведение двухшаговой задачи стохастического оптимального управления с билинейной моделью к задаче смешанного целочисленного линейного программирования. // АиТ. 2016. № 12. С. 89–111.
8. Малышев В.В., Кибзун А.И. Анализ и синтез высокоточного управления летательными аппаратами. М.:Машиностроение, 1987.
9. Jasour A.M., Aybat N.S., Lagoa C.M. Semidefinite Programming For Chance Constrained Optimization Over Semialgebraic Sets // SIAM Journal on Optimization 25 (3), 1411–1440, 2015.
10. Jasour A.M., Lagoa C.M. Convex Chance Constrained Model Predictive Control //arXiv preprint arXiv:1603.07413, 2016.
11. Smith R.L., “Efficient Monte Carlo procedures for generating points uniformly distributed over bounded regions”, Oper. Res., 32:6 (1984), 1296-130