Комплекс программ оптимального раскрашивания множества вершин связного графа с использованием метода ветвей и границ

В статье рассматривается задача об оптимальном раскрашивании вершин графа с использованием метода ветвей и границ. Приводятся примеры практических задач, сводящихся к раскраске графа, а также приводится программа, с помощью которой можно находить оптимальную раскраску для связного графа.

В статье рассматривается задача об оптимальном раскрашивании вершин графа с использованием метода ветвей и границ. Приводятся примеры практических задач, сводящихся к раскраске графа, а также приводится программа, с помощью которой можно находить оптимальную раскраску для связного графа.

ВВЕДЕНИЕ

В настоящее время теория графов активно развивается, так как задачи, решаемые с ее помощью, находят широкое применение на практике. Графы служат удобным средством для визуализации связей между различными объектами и активно применяются в различных сферах человеческой деятельности. Например, схема линий метро является графом. Вершинами данного графа являются станции, а ребрами - пути движения поездов.

Одной из наиболее популярных тем теории графов является раскраска графов. Данная задача появилась в середине 19 века, когда в попытках раскрасить политическую карту была сформулирована проблема четырех красок. В наши дни задача о раскраске графов так же широко изучается, так как находит широкое применение при решении различных практических задач.

1.         ПРАКТИЧЕСКИЕ ЗАДАЧИ, СВОДЯЩИЕСЯ К РАСКРАСКЕ ГРАФОВ

Задача о раскраске графа может широко применяться для решения различных прикладных задача, например:

1.   Задача о минимальном числе помещений для хранения продуктов. Предположим, что необходимо распределить продукты по помещениям. В силу каких-то причин некоторые из продуктов не могут находиться в одном помещении. Требуется распределить продукты по помещениям так, чтобы для распределения продуктов потребовалось минимальное количество помещений.

2.   Задача о частотных диапазонах в станциях сотовой сети. Имеется n вышек сотовой связи, которые расположены так, что у них есть общие зоны покрытия. Так как число диапазонов частот, которые используются в системе мобильной радиосвязи ограниченно, то могут возникать взаимные помехи из-за того, что различные базовые станции (например, с общей зоной покрытия) используют одинаковый диапазон частот. Требуется распределить частоты между базовыми станциями таким образом, чтобы минимизировать помехи, оказываемые станциями друг на друга.

3.   Задача о проектировании коробки скоростей. Коробка скоростей - механизм для изменения частоты вращения ведомого вала при постоянной частоте вращения ведущего. Имеется n шестерней, которые размещаются на валах. Задача, стоящая перед конструктором коробки, заключается в минимизации ее размеров, а это часто сводится к поиску наименьшего числа валов, на которых размещаются шестерни.

4.   Задача о составлении расписаний. Пусть необходимо прочитать несколько лекций за определенное время. Чтение каждой лекции в отдельности занимает один час, но некоторые лекции не могут читаться одновременно. Требуется составить расписание так, чтобы чтение всех лекций заняло минимально возможное время.

2.         МЕТОД ВЕТВЕЙ И ГРАНИЦ

Для решения задачи о раскраске графов существует большое количество различных методов, однако не все из них позволяют находить оптимальную раскраску для графа.

Одним из методов, позволяющих найти оптимальную раскраску для графа, является метод ветвей и границ [Кристофидес, 1978], один из вариантов изложения его применения к указанной задаче приведен в работе [Нефедов, 1994]. Данный метод является модификацией метода полного перебора. Его существенным преимуществом является то, что из рассмотрения исключаются подмножества решений, которые заведомо не дадут оптимального решения. Однако данный метод не подходит для решения задач с большим количеством вершин в графе. Если количество вершин в графе велико, то следует использовать эвристический алгоритм, одно из изложений которого приведено в работе [Нефедов, 2015], который позволяет находить раскраску для графа с практически неограниченным конечным множеством вершин, однако дает оптимальное решение только в некоторых случаях.

3.         ПРИМЕНЕНИЕ АЛГОРИТМА РАСКРАСКИ ГРАФОВ К РЕШЕНИЮ ПРАКТИЧЕСКИХ ЗАДАЧ

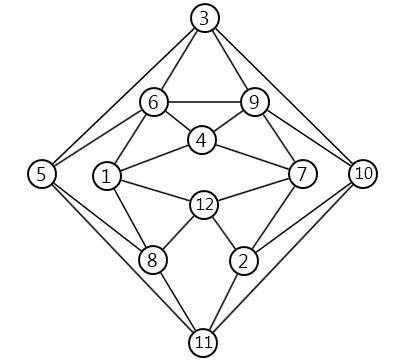
Рис. 1. Исходный граф

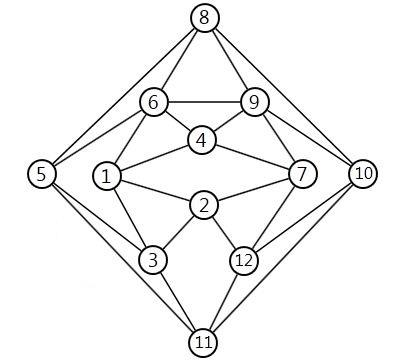
   Рис. 2. Перенумерованный граф

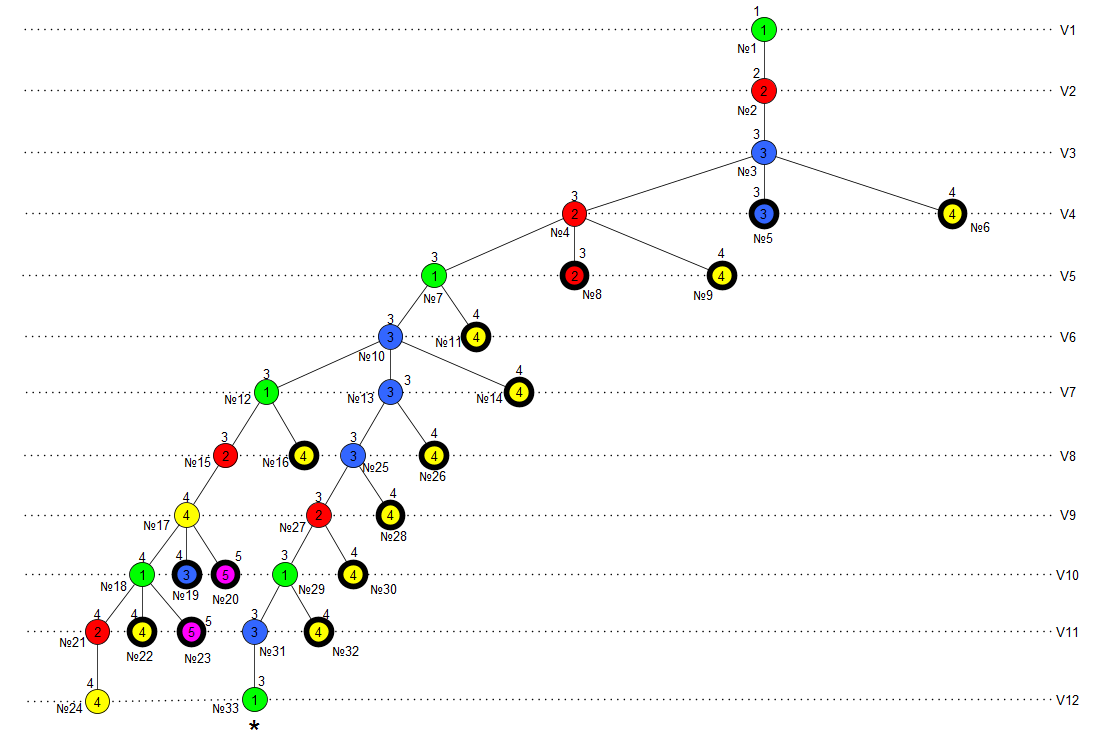
Рис. 3. Результат применения метода ветвей и границ

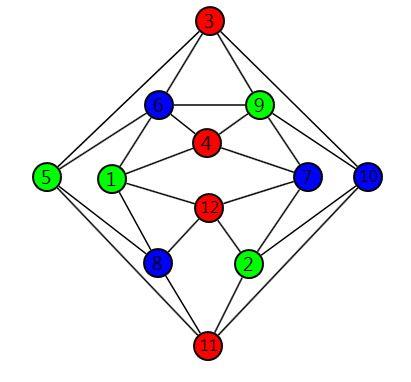
Рис. 4. Раскраска графа

Соответствующий список размещения продуктов по помещениям представлен в таблице. В первом помещении хранятся продукты 1, 2, 5, 9; во втором - 3, 4, 11, 12; в третьем - 6, 7, 8, 10.

Результаты решения задачи

 

4.         ПРОГРАММА ДЛЯ РАСКРАСКИ ГРАФА

Интерфейс программы для раскраски графов представлен на рис. 5. С помощью данной программы можно рисовать разнообразные графы в заданной области, а также находить оптимальную раскраску для этих графов. Для раскраски графов используется метод ветвей и границ.

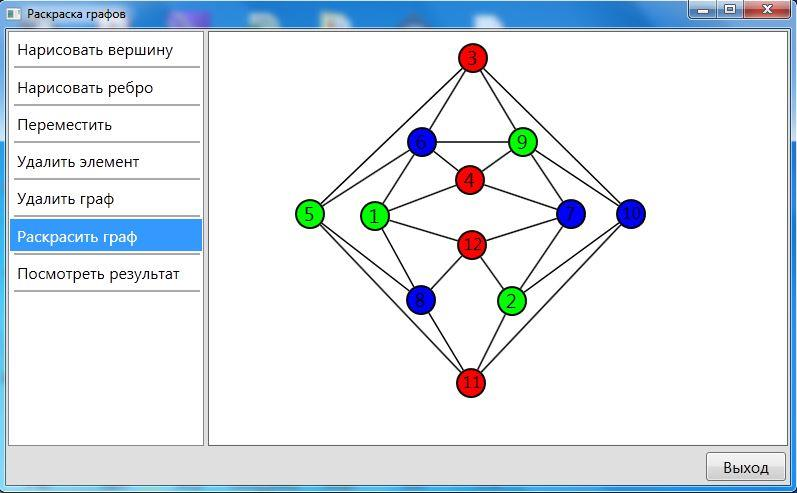
Рис. 5. Интерфейс программы

1. Кристофидес Н. Теория графов. Алгоритмический подход. –М.: Мир, 1978. – 432 с.
2. Конвей Р.В., Максвелл В.Л., Миллер Л.В. Теория расписаний. –М.: Наука, 1975. –360 с.
3. Липский В. Комбинаторика для программистов. –М.: Мир, 1988. –200
4. Шкурба В.В. Задача о трёх станках –М.: Наука, 1976. –92 с.
5. Нефедов В.Н. Методические указания к выполнению расчетных работ по теории гра-фов и сетей. –М.: Доброе слово, 2015. –59 с.
6. Нефедов В.Н. Дискретные задачи оптимизации: Учебное пособие. – М.: Изд-во МАИ, 1994. –59 с.
7. Нефедов В.Н., Осипова В.А. Курс дискретной математики. – М.: Изд-во МАИ, 1992. –264 с.