В статье рассматривается упрощенный метод анализа иерархий. Для формирования матрицы парных сравнений используются алгоритмы теории графов. В качестве модельного примера приводится метод оценки стоимости летательного аппарата при различных формах лизинга.
ВВЕДЕНИЕ

Формирование матрицы парных сравнений в МАИ требует трудоемкой работы с экспертами и не гарантирует необходимого свойства её совместности в частности из-за избыточности и недостоверности информации о сравнениях. Вариант МАИ, предложенный В. Д. Ногиным [Ногин, 2004], оказывается существенно проще классического подхода к МАИ как на стадии формирования матрицы парных сравнений, так и в ходе вычисления весового вектора, позволяя получить схожие результаты.
В данной работе рассматривается подход, связанный с выбором однозначно определяющих матрицу парных сравнений элементов и требующий значительно меньшего числа экспертных оценок, чем в классическом подходе к МАИ. Предлагается его реализация, основанная на использовании алгоритмов теории графов. Рассматривается модельный пример, связанный с авиационным лизингом.
1. УПРОЩЕННЫЙ ВАРИАНТ МЕТОДА АНАЛИЗА ИЕРАРХИЙ

Следовательно, используя элементы первой строки, мы можем построить всю матрицу парных сравнений, которая будет обладать свойством совместности.
В качестве элементов, однозначно определяющих матрицу парных сравнений не обязательно брать только элементы первой строки и можно перечислить все такие наборы элементов, которые однозначно определяют матрицу парных сравнений. В [Ногин, 2004] предложены следующие определения.

Для определения того, какие вершины принадлежат одной компоненте связности, также воспользуемся известным алгоритмом, приведенным, например, в [Андерсон, 2017; Осипова, 2017].
Все изложенные алгоритмы реализованы в программной среде Delphi. Данная программная система позволяет упростить процедуру формирования матрицы парных сравнений при использовании метода анализа иерархий.
На практике эксперт может определять достоверные оценки лишь при сравнении некоторого набора пар элементов и может затрудняться при сравнении всех элементов. Таким образом, при экспертном оценивании для построения матрицы парных сравнений элементов следует осуществить проверку, является ли данный набор элементов базисным (или определяющим) и дать рекомендации в случае, если он таковым не является. Если набор элементов оказался базисным, то, используя свойства 1) - 3), определяем остальные элементы матрицы парных сравнений. В противном случае от эксперта требуется дополнительно сравнить пары элементов. Их количество зависит от числа компонент связности. В частности, если число компонент связности р = 2, то достаточно добавить одну экспертную оценку, чтобы граф стал связным, в общем случае требуется JJ — 1 экспертная оценка. Эксперт сам может выбрать подходящую для него пару элементов из разных компонент связности для оценивания. В результате получается связный порожденный граф, и, следовательно, базисный набор элементов.
В работе [Ногин, 2004] не отмечено, что при использовании упрощенного МАИ для формирования матрицы парных сравнений, вновь полученные элементы матрицы могут иметь значения, выходящие за пределы шкалы, используемой в МАИ. В этом случае следует последовательно сравнивать другие пары элементов, обеспечивающие базисный или определяющий набор, в итеративном режиме получать наиболее достоверные оценки либо отказаться от применения метода.
2. ПРИМЕНЕНИЕ УПРОЩЕННОГО МЕТОДА АНАЛИЗА ИЕРАРХИЙ К ОЦЕНКЕ СТОИМОСТИ ЛЕТАТЕЛЬНОГО АППАРАТА ПРИ ЛИЗИНГЕ
Авиационный лизинг значительно выделяется среди других видов этой услуги ввиду специфики оформления техники и её регистрации, а также наличие регламента постоянного дорогостоящего обслуживания.
Основными видами авиационного лизинга являются финансовый и операционный.
При финансовом лизинге компания-эксплуататор может получить в собственность летательный аппарат (ЛА) после окончания действия договора, либо выкупить его по остаточной стоимости. При операционном лизинге, как правило, происходит неполный износ техники и после окончания срока аренды ЛА может быть возвращен лизингодателю, либо же срок аренды может быть продлен.
Рассматривая предложения лизинговой компании, авиакомпании проводят собственную оценку стоимости предложенных ЛА в соответствии с выбранной стратегией и анализом критериев, характеризующих воздушное судно, а также предложениями на рынке лизинговых услуг.
Рассмотрим следующий модельный пример. Авиакомпания рассматривает возможность сделки по лизингу конкретного самолета (СМ) и хочет оценить разумность стоимости сделки. При этом уже имеются некоторые данные о параметрах сделок с самолетами аналогичного типа (Аналог 1, Аналог 2, Аналог 3, Аналог 4 и Аналог 5).
Проведем сравнение рассматриваемых ЛА с точки зрения привлекательности сделки и оценим стоимость СМ с помощью упрощенного метода анализа иерархий. В нашем случае проводится сравнение между шестью альтернативами А1,А2... А6 (СМ и его аналоги).
Иерархическая структура процесса сравнения представлена на рис.1.
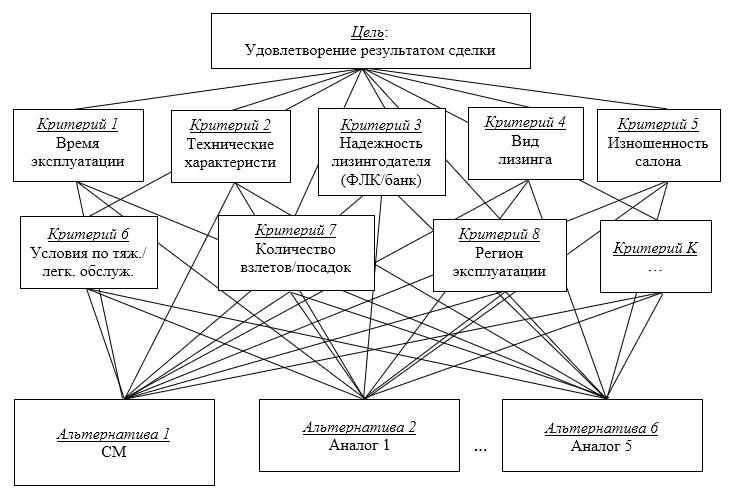
При авиационном лизинге ЛА оценивается с помощью значительного числа критериев. В данном модельном примере ограничим сравнение ЛА с точки зрения привлекательности для лизинга восемью характеристиками, которые определяют критерии качества: - время эксплуатации, — технические характеристики, Кл - надежность лизингодателя (финансовая лизинговая компания/банк), К_ - вид лизинга, - изношенность салона , К.< - условия по тяжелому/легкому обслуживанию, К- - количество взлетов/посадок, Ка - регион эксплуатации. При сравнивании каждого ЛА по этим критериям дается оценка по девятибалльной шкале [Саати, 1989]: например, разница в 15 лет времени эксплуатации составляет значительное преимущество по сравнению с менее новым и оценивается в 7 баллов.
Матрица парных сравнений критериев К1, К2, К3, К4, К5, К6, К7, К8 относительно общей удовлетворенности покупкой представлена табл. 1.
Таблица 1 Матрица парных сравнений критериев
|
|
К. |
к2 |
к3 |
к, |
К5 |
к6 |
к7 |
К3 |
|
К1 |
1 |
3 |
5 |
7 |
9 |
7 |
5 |
7 |
|
к2 |
1/3 |
1 |
3 |
5 |
7 |
9 |
7 |
5 |
|
К3 |
1/5 |
1/3 |
1 |
3 |
5 |
7 |
9 |
7 |
|
к4 |
1/7 |
1/5 |
1/3 |
1 |
3 |
5 |
7 |
9 |
|
К5 |
1/9 |
1/7 |
1/5 |
1/3 |
1 |
3 |
5 |
7 |
|
К6 |
1/7 |
1/9 |
1/7 |
1/5 |
1/3 |
1 |
3 |
5 |
|
К7 |
1/5 |
1/7 |
1/9 |
1/7 |
1/5 |
1/3 |
1 |
3 |
|
K8 |
1/7 |
1/5 |
1/7 |
1/9 |
1/7 |
1/5 |
1/3 |
1 |

Из этого следует, что в нашем примере наиболее важная характеристика - время эксплуатации, затем идут технические характеристики, надежность лизингодателя, вид лизинга, изношенность салона, условия по тяжелому/легкому обслуживанию, количество взлетов/ посадок, регион эксплуатации.
Сравнение предложенных для лизинга ЛА по каждому из восьми выбранных критериев проводится экспертом и определяется матрицами парных сравнений. Как правило, эксперт не может достаточно достоверно определить все значения матрицы парных сравнений. В табл. 2 представлены оценки эксперта при сравнении рассматриваемых ЛА с точки зрения критерия КИ «Изношенность салона».
Таблица 2 Исходная матрица парных сравнений
|
К5 |
СМ |
Аналог 1 |
Аналог 2 |
Аналог 3 |
Аналог 4 |
Аналог 5 |
|
СМ |
1 |
|
1/8 |
|
|
|
|
Аналог 1 |
|
1 |
1/2 |
|
|
|
|
Аналог 2 |
|
|
1 |
|
|
|
|
Аналог 3 |
|
|
|
1 |
1/5 |
|
|
Аналог 4 |
|
|
|
|
1 |
3 |
|
Аналог 5 |
|
|
|
|
|
1 |
Представим матрицу парных сравнений в виде графа, изображенного на рис.2.:
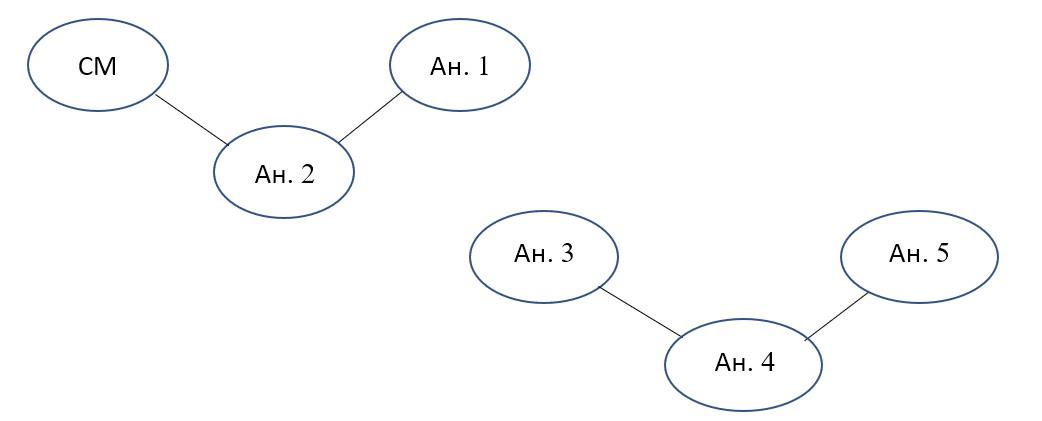
Рис. 2. Граф первоначальной матрицы парных сравнений
Число компонент связности этого графа р = 2 Следовательно, набор элементов не является базисным. Для матриц большого порядка следует использовать алгоритм Уоршелла проверки связности для порожденного графа, который позволяет определить является ли набор базисным. Т.к. р = 2, то достаточно добавить одну оценку, сравнивая любую вершину одной компоненты связности с любой вершиной другой компоненты. Допустим, исходя из экспертного анализа, было дополнительно проведено сравнение аналога 2 и аналога 3. Граф окончательной матрицы парных сравнений представлен на рис.3. Найден базисный набор элементов, по которому сможем найти остальные элементы матрицы парных сравнений, представленные в табл.3.
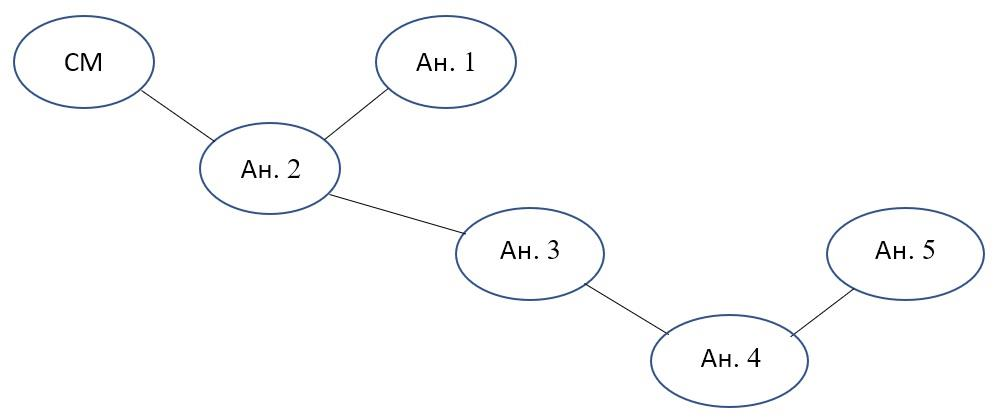
Рис. 3. Граф окончательной матрицы парных сравнений
Таблица 3 Окончательная матрица парных сравнений
|
|
СМ |
Аналог 1 |
Аналог 2 |
Аналог 3 |
Аналог 4 |
Аналог 5 |
|
СМ |
1 |
1/4 |
1/8 |
7/8 |
7/40 |
21/40 |
|
Аналог 1 |
4 |
1 |
1/2 |
7/2 |
7/10 |
21/10 |
|
Аналог 2 |
8 |
2 |
1 |
7 |
7/5 |
21/5 |
|
Аналог 3 |
8/7 |
2/7 |
1/7 |
1 |
1/5 |
3/5 |
|
Аналог 4 |
40/7 |
10/7 |
5/7 |
5 |
1 |
3 |
|
Аналог 5 |
40/21 |
10/21 |
5/21 |
5/3 |
1/5 |
1 |
