Исследование модифицированной стратегии последовательного хеджирования с наклонной полосой нечувствительности

В настоящей работе рассматривается модификация стратегии последовательного хеджирования опциона, при которой вводится полоса нечувствительности. Верхняя граница данной полосы имеет наклон. В ходе работы была рассмотрена математическая модель с дискретным процессом ценообразования. Приращения данного процесса имеют нормальное распределение с постоянным ненулевым средним и постоянной дисперсией. В статье рассматривается распределение числа пересечений непрямолинейной полосы дискретным гауссовским блужданием. Составлены формулы, которые позволяют задать распределение числа пересечений полосы в направлениях «снизу-вверх» и «сверху-вниз». Был составлен алгоритм подсчета количества этих пересечений и оценки условной вероятности перехода. Помимо этого была рассмотрена зависимость средних потерь хеджера при использовании данной стратегии от коэффициента наклона верхней границы полосы нечувствительности и ширины полосы. С использованием моделирования по методу Монте-Карло был составлен алгоритм поиска оптимальный ширины и наклона полосы. В ходе проведения численных экспериментов была выявлена зависимость и определен оптимальный коэффициент наклона при заданных параметрах. Экспериментальная работа подтвердила корректность предложенных алгоритмов и доказала эффективность данной модификации в сравнении с использование стратегии с прямолинейной полосой.

В настоящей работе рассматривается модификация стратегии последовательного хеджирования опциона, при которой вводится полоса нечувствительности. Верхняя граница данной полосы имеет наклон. В ходе работы была рассмотрена математическая модель с дискретным процессом ценообразования. Приращения данного процесса имеют нормальное распределение с постоянным ненулевым средним и постоянной дисперсией.

В статье рассматривается распределение числа пересечений непрямолинейной полосы дискретным гауссовским блужданием. Составлены формулы, которые позволяют задать распределение числа пересечений полосы в направлениях «снизу-вверх» и «сверху-вниз». Был составлен алгоритм подсчета количества этих пересечений и оценки условной вероятности перехода. Помимо этого была рассмотрена зависимость средних потерь хеджера при использовании данной стратегии от коэффициента наклона верхней границы полосы нечувствительности и ширины полосы. С использованием моделирования по методу Монте-Карло был составлен алгоритм поиска оптимальный ширины и наклона полосы. В ходе проведения численных экспериментов была выявлена зависимость и определен оптимальный коэффициент наклона при заданных параметрах. Экспериментальная работа подтвердила корректность предложенных алгоритмов и доказала эффективность данной модификации в сравнении с использование стратегии с прямолинейной полосой.

Введение

Рынок производных финансовых инструментов является перспективным сегментом ценных бумаг в Российской Федерации. Он привлекает инвесторов возможностью получения прибыли, превосходящей по величине прибыль от операций на рынке акций. Помимо этого, инвестору предоставлен широкий спектр срочных контрактов, которые он может заключить. Это позволяет хеджировать риски при инвестировании в акции, т.е. страховать свои риски.

Одним из типов срочных контрактов является опцион. Он представляет из себя договор между покупателем и продавцом, по которому представляется возможность купить или продать актив по цене, оговоренной на момент заключения сделки в течение определенного промежутка времени. В отличии от форварда, опцион не является обязательным к исполнению, т.е. покупатель может исполнить или не исполнить его по собственному желанию. При заключении договора, продавец берет на себя риск, связанный с возможным изменением цены актива, за что получает денежную премию, именуемую стоимостью опциона. Опционы можно разделить на колл опциона, который дает право на покупку актива по контрактной цене, и пут-опцион, который дает право на продажу по оговоренной цене. По времени исполнения на американский опцион и европейский, т.е. исполнен в течение некоторого промежутка времени или в определенное время, соответственно.

Для того, чтобы минимизировать риски неблагоприятного изменения цены опциона, продавец может использовать часть премии, на формирование инвестиционного портфеля. В него могут входить другие финансовые инструменты. Продавец управляет своим портфелем таким образом, чтобы компенсировать риск опционной позиции. Эта стратегия называется хеджированием, а лицо, управляющее портфелем - хеджером.

Теория страхования срочных позиций начала активно развиваться во второй половине XX века. Одной из фундаментальных работ по теории срочных контрактов является результат работы Ф.Блэка и М.Шоулса [4], полученный в 1973 г. Ими была выведена формула оценки премии европейского колл-опциона и построена модель, которая подразумевает то, что премия опциона может быть произведена в непрерывной пере­балансировкой инвестиционного портфеля. На управление таким портфелем хеджер затрачивает в среднем всю премию за опцион.

Данная модель является справедливой при «идеальных» условиях рынка ценных бумаг, при которых не имеется ограничений на короткие продажи, а сделки могут совершаться мгновенно. При этом необходимо, чтобы базовый актив являлся ликвидным, иначе необходимо учитывать неизвестную длительность транзакций, при управлении финансовым портфелем.

Существует несколько стратегий хеджирования опционной позиции. Одной из них является стратегия последовательного хеджирования, которая позволяет хеджеру обезопасить себя от колебаний цены по всем параметрам.

Стратегия последовательного хеджирования состоит в том, что в случае, если цена базового актива становится больше цены поставки, то производится полное покрытие опционной позиции, в ином случае, активы продаются. Это позволяет избежать потерь, связанных с возможным падением цены актива в дальнейшем. Перебалансировка портфеля производится только в случае пересечения ценой базового актива уровня поставки.

Впервые стратегия последовательного хеджирования была рассмотрена в работе Сей- нденверга под названием «Stop-loss start-gain strategy» [6]. Дальнейшее развитие эта стратегия получила в работе П.Карра [5], где была доказана несамофинансируемость модели. Так же, была выведена новая формула расчета стоимости европейского колл-опциона на основе данной стратегии.

В России данной проблемой занимался Буренин [1]. Благодаря ему она получила название «стратегия последовательного хеджирования». В статье А.И. Кибзуна и В.А. Гу- берниева [2] была рассмотрена дискретная мультипликативная модель ценообразования акций базового актива. В их работе была проведена оценка ожидаемых потерь хеджера при использовании стратегии последовательного хеджирования.

При данной стратегии перебалансировка портфеля ценных бумаг производится в случае, если рыночная цена актива достигает цены поставки. Но это приводит к тому, что при высокой частоте колебаний курса относительно цены поставки, хеджер несет неоправданно высокие потери.

Для того чтобы избежать данную проблему, в статье А.И. Кибзуна и В.Р. Соболя [3] была рассмотрена модернизация стратегии последовательного хеджирования. Ими было введено понятие полосы нечувствительности, которая предполагает, что продажа и покупка актива совершается не при пересечении цены поставки, а при пересечении этой полосы, которая включает в себя цену поставки. При пересечении верхней границы полосы «снизу-вверх» опционная позиция будет открытой, в случае пересечения нижней границы «сверху-вниз» - позиция закрыта. В работе была рассчитана оптимальная ширина полосы, при которой потери хеджера минимальны.

В данной статье рассматривается непрямолинейная полоса нечувствительности, при которой нижняя граница является зафиксированной, а верхней задается наклон. В качестве верхней границы полосы используем прямую с отрицательным коэффициентом наклона, что соответствует сужающейся полосе. Это должно обеспечить меньшие затраты на закрытие позиции - уменьшается спред между ценой покупки и продажи, - при приближении срока исполнения опциона и текущей ценой актива, превышающей страйк. Исследуется зависимость средних затрат хеджера от наклона верхней границы полосы нечувствительности и ее ширины.

Постановка задачи

2.     РАСПРЕДЕЛЕНИЕ ЧИСЛА ПЕРЕСЕЧЕНИЙ ПОЛОСЫ

Средние затраты хеджера

При использовании стратегии последовательного хеджирования хеджер может нести убытки. В случае, если цена базового актива пересекает верхнюю полосу «снизу вверх»,то хеджер приобретает базовый актив в полном объеме. В случае, когда цена пересекает цену поставки «сверху вниз» хеджер продает все активы. Введем величину l_i ,которая определяет потери хеджера на i -ом шаге:

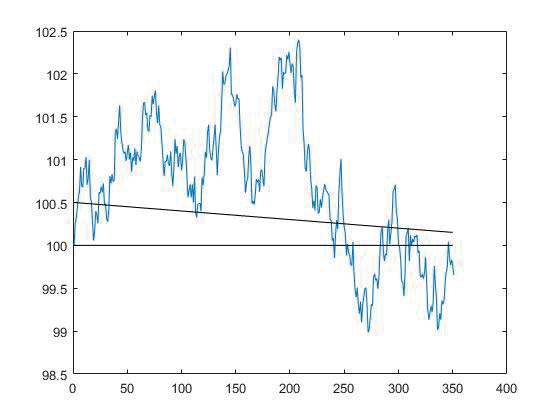
Рис. 1. Результат работы алгоритма 1.

Вероятность последовательности состояний

Вероятность перехода на заданном шаге

Алгоритм поиска оптимальной ширины и коэффициента наклона полосы

Как говорилось ранее, средние потери хеджера зависят от количества пересечений полосы нечувствительности. Таким образом, изменяя ширину полосы и коэффициент наклона, можно определить их значения таким образом, что потери хеджера будут минимальны. Сформулируем алгоритм поиска оптимального соотношения параметра d и q .

Алгоритм 3:

1.      Сгенерируем приращения для каждого шага от 1 до Т с помощью S1 = normrnd(0, sigma, N, M).

2. Зададим шаг изменения коэффициентов d и q. Пусть a -шаг коэффициента d, а ai - шаг коэффициента q.

3.     Зададим процесс изменения цены

4.     Если Si > k (1 + d) + q и предыдущая позиция опциона была открытой, то x_t = 0, x_t_1 = 1 и l = l + S перейти к шагу 8.

5.     Если Si < k (1 + d) + q и предыдущая позиция опциона была открытой, то x_t = 0, а x_t_1 = 0, перейти к шагу 8.

6.     Если Si < k и предыдущая позиция опциона была открытой, то xi = 1, а x_t_₁ = 0 и положить l = l _ S и перейти к шагу 8 .

7.     Если S_i > k и предыдущая позиция опциона была открытой, то x_i = 1 , а x_{i_1} = 1 и перейти к шагу 8.

8.     Если i > N, то вычислить 12 = l / N и перейти к шагу 9, иначе положить i = i +1, d = d + a и перейти к шагу 4.

9.     Если j = M, то вычислить L2 = 12/ N и перейти к шагу 10, иначе положить j = j +1 и перейти к шагу 3.

10.    Если q1 = m -положить q = q + a1, перейти к шагу 4

11.   Найти индекс минимального элемента массива larray, сопоставить его с элементом массива darray и qarray, построить график. Алгоритм закончен.

Результаты численных экспериментов

Воспользуемся полученным алгоритмом. Зададим начальные параметры:

Пусть начальная цена базового актива S = 100 у.е., цену поставки актива возьмем равным k = 100у.е. Количество шаговN примем равным 10,  = 0,2 .

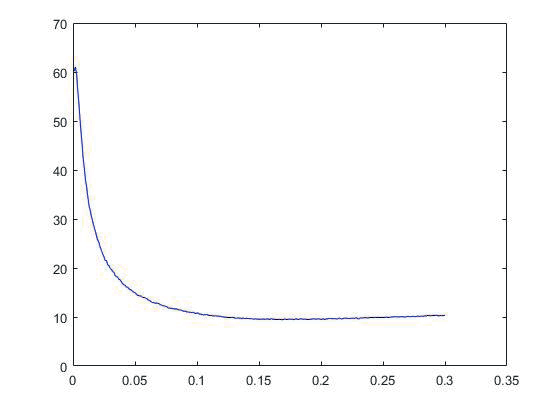
Рис. 2. Результат работы алгоритма 2.

 

В ходе работы алгоритма было получено, что минимальные потери, при заданных параметрах, хеджер несет при ширине полосы d = 0,18 и коэффициенте наклона q = 0, 0005 .

На основании полученных результатов можно утверждать, что данный метод, в сравнении с модификацией стратеги последовательного хеджирования, при которой вводится полоса нечувствительности с зафиксированной верхней границей, позволяет уменьшить потери хеджера.

Результаты доказывают, что хеджер не понесет убытков с ненулевой вероятностью.

 

1. Буренин А.Н. “Рынки производных финансовых инструментов“ М.:Инфра-М, 1996
2. Губерниев В.А., Кибзун А.И. Последовательное хеджирование опционной позиции: анализ и модернизация // Автоматика и телемеханика.- 1999.-№ 1.-С. 113–125
3. Кибзун А.И., Соболь В.Р., “Двухшаговая задача хеджирования европейского колл-опциона при случайной длительности транзакций“// Тр. Ин-та математиуи и механики УрО РАН. 2015. Т. 21, № 3. С.164–174
4. Кибзун А.И., Соболь В.Р., “Модификация стратегии последовательного хеджирования. Распределение потерь хеджера.»// УПРАВЛЕНИЕ БОЛЬШИМИ СИСТЕМАМИ Материалы XI всероссийской школы-конференции молодых ученых. 2014. C. 580–591
5. Black F., Scholes M. “The Pricing of Options and Corporate Liabilities“ // Journal of Political Economy. 1973. Vol. 81. № .3. P. 637–659
6. Carr P., Jarrow R. “The Stop-Loss Start-Gain Paradox and Option Valuatuin: a New Decomposition into Intrinistic and Time Value“ // Review of Financial Studies. 1990. V. 3. № .3 P.469–492.
7. Seidenverg E. “A Case of Confused Identity“ // Financial Analysts Journal. 1988. P. 63–67

PlumX

Метрики публикации