Осязательные модели в аналитической геометрии

В статье обсуждаются некоторые проблемы, возникающие при работе со студентами, имеющими дефекты зрения. В частности, авторы обсуждают пути повышения культуры математического мышления студентов с дефектами зрения. Авторы опираются на опыт работы на факультете информационных технологий МГППУ.

1.             ВВЕДЕНИЕ

На факультете информационных технологий МГППУ студентам с дефектами зрения преподаются различные разделы высшей математики. Естественно, что в такой ситуации ведётся активная деятельность, связанная с методической проработкой некоторых вопросов тифлопедагогики. Примером являются статьи [1 – 3]. Данная статья также направлена на разработку некоторых проблем преподавания высшей математики в рамках тифлопедагогики.

В ходе изучения математических дисциплин студенты с дефектами зрения очень часто работают с разного рода математическими объектами. В большинстве случаев они бывают представлены в виде плоскопечатных изображений. В связи с этим незрячие студенты испытывают ряд определённых трудностей при прохождении учебного материала. Они не могут, например, рассмотреть рисунок, который прилагается к параграфу в учебнике или лекции. Словесного описания со стороны преподавателя, зрячего студента или какого-либо другого зрячего человека порой бывает недостаточно для понимания сути рисунка. Таким образом, незрячие студенты, в лучшем случае, понимают материал недостаточно чётко, в худшем случае, понимают его неправильно.

Возникают проблемы и при решении задач. Вышеописанная проблема с рассмотрением рисунков в этом случае тоже присутствует: Незрячие студенты, не имея возможности видеть и чётко понимать рисунок, данный к задаче, либо абсолютно не справляются с решением поставленной задачи, либо справляются, но не в полной мере, без должного понимания сути задачи и путей её решения.

Кроме того, проблема может возникнуть и непосредственно при решении задач. Фактически студент должен сам создать какой-либо рисунок для тех или иных целей. Например, если в ходе решения задачи  от студентов требуется создать график или какой-либо другой рисунок, то велика вероятность того, что незрячие студенты не смогут этого сделать.

Не стоит отрицать, что существуют специальные приборы, предназначенные для черчения рельефных графиков. Но с ними тоже связано немало проблем: Во-первых, работа с ними занимает большое количество времени, что неприемлемо при работе в группе; Во-вторых, точность чертежей, созданных при помощи этих приборов, оставляет желать лучшего.

Осязательные модели поспособствуют решению если не всех, то многих из этих проблем. Они должны существенно улучшить качество обучения незрячих студентов. Благодаря им обучение незрячих студентов станет более простым и эффективным. При помощи этих моделей можно будет более наглядно показать незрячим студентам, как выглядят математические объекты. Это даст следующие преимущества: во-первых, модели сыграют важную роль при первом знакомстве с математическими объектами; во-вторых, модели помогут решить описанные выше проблемы при изучении теоретического материала и при решении задач. Модели позволят легко и быстро изобразить тот или иной рисунок. Будь то рисунок, связанный с изучаемой темой, или рисунок в условии задачи. Модели помогут также и непосредственно при решении. С их помощью можно будет свободно воспринимать математические объекты, формируя образы, необходимые для решения тех или иных задач.

Конкретно тематика статьи связана с вопросами аналитической геометрии. Основные идеи, положенные в её основу таковы. Прежде всего, метод координат является основой не только аналитической геометрии, но и практически всех разделов классической математики. По этой причине глубокое понимание аналитической геометрии и свободное владение её методами позволяет открыть путь к освоению курса высшей математики в целом. Центральную роль при этом играют темы, связанные с изучением кривых второго порядка.

Аналитическая геометрия, как и другие разделы геометрии, основывается на образном восприятии многих понятий [4]. Естественно, что важной опорой в обучении этому предмету являются чертежи и рисунки, позволяющие воспринимать многие геометрические конструкции как целое. К сожалению, студенты, имеющие дефекты зрения, такой возможности лишены.

Заменой чертежей и рисунков могут стать осязательные модели, позволяющие детально разобраться с теми же геометрическими конструкциями путём осязательной работы с их материальными аналогами.

Авторы статьи работают над данной тематикой два года. За время работы при сохранении общей цели работы несколько изменился её акцент. Причины этого изменения таковы. Первая модель, рассмотренная авторами, представляла собой материальный объект, играющий роль декартовой плоскости. К этой модели должны были прилагаться модели геометрических линий, в частности, прямых. Основной методической задачей при этом была разработка заданий, относящихся к аналитической геометрии и одновременно адаптированных к соответствующим осязательным моделям.

Работа была проделана, однако, возникла проблема, связанная с тем, что все осязательные модели остались лишь теоретическими проектами. Изготовление этих моделей требовало привлечения специалиста, поскольку разработчики проекта не имели возможности самостоятельно выполнить данную работу. Следует отметить, что упомянутые модели не являются слишком сложными объектами. Возможно кустарное их изготовление. Но для этого во-первых необходимы определённые материальные затраты, пусть и небольшие. Речь идёт о материалах и наличии инструментов. Главная же проблема связана с тем, что указанные работы требуют довольно значительного времени.

Именно по этой причине на следующем этапе работы авторы приняли решение о том, что осязаемые модели, кроме всего прочего, должны удовлетворять следующему дополнительному требованию: их изготовление может быть проведено в бытовых условиях без значительных материальных затрат с использованием инструментов и материалов, которые можно найти в любом доме.

Таким образом, данная работа разделилась на два блока, которые с педагогической и методической точки зрения едины, но которые разделены в технологическом отношении. Ниже будут изложены результаты, полученные на обоих этапах работы. При этом результаты второго из этих этапов будут, в первую очередь, содержать описание технологий, направленных на самостоятельное изготовление соответствующих осязательных моделей. При этом процесс их изготовления будет довольно подробно описан, а иногда и проиллюстрирован. Это, несомненно, может помочь лицам, пожелавшим самостоятельно воспроизвести, а затем и использовать эти модели. Кроме того, авторы хотят отметить, что предлагаемые ими модели и технологии их изготовления могут быть модифицированы и усовершенствованы пользователями.

2.             О ПОСЛЕДОВАТЕЛЬНЫХ СТАДИЯХ РАЗРАБОТКИ ОСЯЗАТЕЛЬНЫХ МОДЕЛЕЙ

Прежде чем говорить о разработанных авторами статьи осязательных моделях, опишем основные стадии разработки таких моделей. Как отмечалось выше, некоторые стадии по ряду обстоятельств могут быть пропущены. Обычно это относится к стадии изготовления рабочей модели. Однако полноценная работа над созданием осязательных моделей должна осуществляться без подобных лакун. Это, конечно же, требует достаточно серьёзной технологической поддержки.

 

·               Последовательный обзор избранной для методической проработки математической темы и выделение понятий и разделов, которые должны быть проиллюстрированы с помощью осязательных моделей.

·               Изобретение осязательных моделей, дающих возможность изменить или расширить возможности традиционной методики преподавания.

·               Разработка технологии изготовления соответствующей осязательной модели.

·               Изготовление осязательной модели с фиксацией всех технологических стадий.

·               Анализ исходного технологического плана и сравнение его с реальным процессом изготовления осязательной модели.

·               Улучшение технологии изготовления соответствующей осязательной модели с учётом уже проделанной работы.

·               Эксперименты с осязательной моделью с целью проверки её пригодности для обучения студентов с дефектами зрения.

·               Создание текста инструкции, предназначенной для студентов с дефектами зрения, осваивающих данную осязательную модель.

·               Создание аудиофайла соответствующей инструкции, позволяющего студентам с дефектами зрения освоить данную осязательную модель без посторонней помощи.

·               Разработка системы заданий, при решении которых можно использовать данную осязательную модель.

·               Проведение педагогических экспериментов, позволяющих улучшить систему заданий по изучаемой математической теме.

 

Естественно, что изучение целостного математического курса охватывает сразу несколько более узких тем и соответственно требует использования нескольких осязательных моделей. В свою очередь здесь могут возникнуть дополнительные проблемы, связанные с методической проработкой данного курса.

3.             ОСЯЗАТЕЛЬНАЯ МОДЕЛЬ ДЕКАРТОВОЙ ПЛОСКОСТИ И ПРЯМЫХ

В данной работе будут рассмотрены модели декартовой плоскости и двух прямых. Они помогут при решении ряда задач, связанных с графиками линейных функций. Подробнее эти задачи будут рассмотрены ниже.

Модель декартовой плоскости имеет одну особенность: При рассмотрении разных функций студенты нередко сталкиваются с дробными координатами; модель не предоставляет возможности работы с ними. С помощью модели можно работать только с целочисленными координатами.

Несмотря на эту особенность, модель внесёт значительный вклад в развитие обучения незрячих студентов: она поможет как студентам при изучении материала, так и преподавателям при объяснении материала незрячим студентам.

Приступим к описанию осязаемой модели декартовой плоскости.

Моделью декартовой плоскости является квадратный лист толстой фанеры. Сначала он покрывается сеткой квадратов 20 на 20. В узлах сетки в листе фанеры просверливаются сквозные отверстия (рис. 1). При работе с моделью они будут играть роль точек на координатной плоскости. Узел (10; 10) считается началом системы координат. На листе фанеры намечаются оси координат, например, с помощью неглубокого пропиливания.

 

 

Рис. 1

 

Сквозные отверстия будут играть роль точек на координатной плоскости, и, как мы увидим далее, в эти отверстия будут вставляться стерженьки, к которым будут прикреплены спицы, моделирующие прямые линии. По этой причине для удобства работы с моделью её следует снабдить ножками (рис. 2). Это позволит без проблем закреплять на модели декартовой плоскости те же самые прямые, а в принципе и модели других линий, изучаемых в аналитической геометрии.

 

 

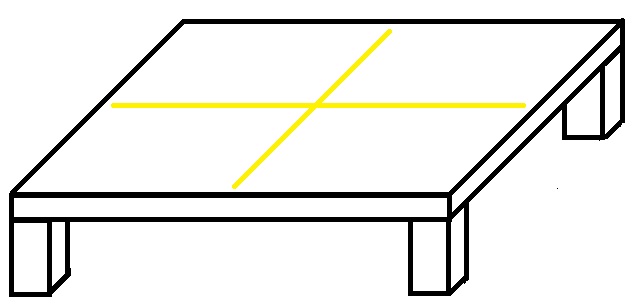
Рис. 2

 

Перейдём к рассмотрению моделей прямых. Моделью прямой является спица, на которую надеты два стерженька (рис. 3), которые могут свободно скользить вдоль спицы. Стерженьки позволяют зафиксировать положение двух точек на прямой. Отметим, что модель прямой, в отличие от модели декартовой плоскости, была реализована. Роль собственно прямой играла вязальная спица, а стерженьки были изготовлены из скрепок.

 

 

Рис. 3

 

Подобная модель прямой может быть прикреплена к модели декартовой плоскости с помощью вставки стерженьков в отверстия. После этого положение прямой на плоскости можно осязать. И, в том числе, можно на ощупь определить координаты двух точек, задающих положение прямой.

Естественно, при рассмотрении задач аналитической геометрии, связанных со взаимном положением прямых, следует использовать по крайней мере хотя бы ещё одну такую же модель прямой. Ясно, что конструкции соответствующих моделей позволяют рассматривать, например, пересекающиеся прямые.

Была разработана система заданий. Первая группа задач, связана с вопросами, относящимися к одной прямой. Уравнения прямой при этом задаются конкретными параметрами.

Соответствующие задачи можно сформулировать в общем виде, но при этом предполагается, что значения параметров являются целыми числами, соотносящимися с размерами и возможностями модели. Кроме общей формулировки каждое задание сначала будет решаться при конкретных значениях параметров, иногда выбранных так, чтобы сделать вычисления максимально простыми.

Задачи с определённой точки зрения являются весьма простыми, но не следует забывать, что речь идёт о методических разработках в области тифлопедагогики. После рассмотрения ряда заданий мы вернёмся к обсуждению данной темы.

1.             С помощью параметров k и b задано уравнение прямой . Прикрепить модель прямой к модели плоскости так, чтобы уравнение прямой соответствовало заданным параметрам.

Решение. Пусть k = 3 и b = 2. Для выполнения задания сначала нужно определить две точки, через которые проходит заданная прямая. Это делается с помощью подстановки в уравнение целочисленных значений аргумента и нахождения соответствующее значение функции.

Например, пусть x = 0. Подставим это значение в функцию y = 3x + 2, находим значение y = 2. Одна из двух точек найдена.

Теперь найдём вторую точку. Пусть x = 1. Подставим это значение в функцию и найдём значение y = 5. Вторая точка тоже найдена.

Таким образом, прямая проходит через точки (0; 2) и (1; 5). После нахождения координат точек необходимо на модели плоскости найти отверстия, соответствующие этим точкам, а затем прикрепить прямую к плоскости, вставив стерженьки в нужные отверстия. Задача решена.

2.               Прямая прикреплена к плоскости. Получить её уравнение.

Решение. Сначала необходимо определить, через какие точки проходит прямая, то есть найти отверстия на модели плоскости, в которые вставлены стерженьки прямой. Например, пусть прямая проходит через точки (1; 1) и (2; 2). На этом основании нужно составить систему из двух уравнений, каждое из которых имеет вид . Поскольку y – ординаты точек, x – абсциссы точек, а k и b – неизвестные коэффициенты. Система уравнений в нашем случае принимает вид

 

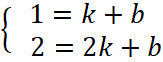
Решая систему, получаем, что k = 1 и b = 0. Таким образом, уравнение прямой имеет вид . Задача решена, но студент может, используя осязание, дополнительно убедиться, что именно эта формула описывает прямую. Для этого достаточно сравнить абсциссы и ординаты точек прямой и убедиться, что они равны.

3.             Пусть параметры k и b задают уравнение прямой. Кроме того дана точка (х₁; у₁). Прикрепить прямую, проходящую через эту точку, параллельно исходной прямой.

Решение. Пусть k = 0, b = 1, x₁ = 0, y₁ = –1. Такие исходные данные могут показаться слишком простыми, но в области тифлопедагогики нужно рассматривать разнообразные варианты, в том числе и случай горизонтальной прямой.

Чтобы точно определить место расположения искомой прямой, нужно найти ещё одну точку, через которую она проходит. Для этого, в свою очередь нужно вывести уравнение искомой прямой.

Пусть k₁ – угловой коэффициент искомой прямой, b₁ – свободный коэффициент в уравнении искомой прямой. Тогда уравнение этой прямой примет вид . Известно, что у параллельных прямых угловые коэффициенты равны. В нашем примере k₁ = k = 0.

Чтобы найти коэффициент b₁, подставим в уравнение  координаты точки (х₁; у₁), данные в условии. В итоге получаем, что . Таким образом, уравнение искомой прямой принимает вид .

Теперь приступим непосредственно к поиску второй точки, через которую проходит прямая. Положим x = 1. Подставим это значение в уравнение и получим вполне ожидаемое значение ординаты: .

Итак, прямая проходит через точки (0; ) и (1; ). Теперь нужно найти на модели плоскости отверстия, соответствующие вышеуказанным точкам, и вставить в них стерженьки прямой. Задача решена.

4.             Заданы параметры k и b, задающие уравнение прямой и точка (х₁; у₁). Прикрепить прямую, проходящую через эту точку, перпендикулярно исходной прямой.

Решение. Пусть k = 1, b = 0, x₁ = –1 y₁ = 1. Сначала выведем уравнение искомой прямой. Пусть k₁ – угловой коэффициент искомой прямой, b₁ – свободный коэффициент в уравнении искомой прямой. Тогда уравнение искомой прямой примет вид . Известно, что для перпендикулярных прямых 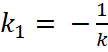. В нашем примере .

Теперь найдём коэффициент b₁. Подставим в координаты данной в условии точки в уравнение  и установим, что . Коэффициенты найдены, а, значит, уравнение искомой прямой имеет вид .

Теперь найдём вторую точку, через которую проходит прямая. Пусть x = 1. Подставим это значение в уравнение прямой и получим, что . Итак, прямая проходит через точки ( 1; 1) и (1; 1). Наконец, необходимо найти на модели плоскости отверстия, соответствующие указанным выше точкам и вставить в них стерженьки прямой. Задача решена.

5.             Даны координаты двух точек (x₁; y₁) и (x₂; y₂). Прикрепить прямую и получить её уравнение.

Решение. Пусть x₁ = 2, y₁ = 2, x₂ = 1, y₂ = 1. Чтобы прикрепить прямую, найдём на модели плоскости отверстия, соответствующие точкам, данным в условии, и вставим в них стерженьки прямой.

Теперь выведем уравнение прямой. Составим систему уравнений вида

 

 

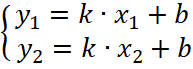
Подставим в систему конкретные координаты точек. Система примет вид.

 

 

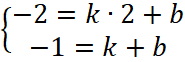
Решаем систему и получаем, что коэффициент  и коэффициент . Уравнение прямой имеет вид . Задача решена.

Можно предположить, что столь подробное рассмотрение столь простых задач, может вызвать определённые возражения со стороны педагогов-математиков. Тем не менее, авторы статьи считают, что тексты, описывающие ход решения, полезны для студентов с дефектами зрения. Более того, эти тексты желательно перевести в аудиофайлы, чтобы, пользуясь ими, студент мог разбираться в соответствующих вопросах без посторонней помощи.

Одним из общих положений педагогической науки является утверждение о том, что построение учебного курса должно определяться целями, которые ставит перед собой преподаватель. При изучении математики часто неявно предполагается, что целью является создание условий для максимального развития математических способностей талантливых студентов. При этом студенты, испытывающие затруднения, как бы выносятся за скобки. В тифлопедагогике такой подход недопустим. Здесь нужно подать учащемуся руку и подвести его к должной степени понимания материала. Возможно, что так следовало бы поступать в отношении всех учащихся вообще. Но это вопрос к общей структуре и общества в целом, и системы образования. Каждый человек уникален, но его уникальность иногда становится препятствием в учёбе. Если общество настроено на максимальное развитие каждого своего члена, оно должно учитывать это обстоятельство. Но тут речь идёт о построении совершенно иного мира.

Естественно, что от задач с простыми и удобными для вычислений данными следует постепенно переходить к более сложным в вычислительном плане задачам. Кроме того, в предлагаемой методике имеется специфическая сторона, связанная с прикреплением модели прямой к модели плоскости. При достижении достаточной степени понимания проблематики студенту следует отойти от использования осязательных моделей и решить все задачи в общем виде.

Имея всё сказанное в виду, перейдём к заданиям, связанным с двумя прямыми.

1.             Даны уравнения двух прямых  и . Прикрепить соответствующие прямые к плоскости и найти решение системы уравнений.

Решение. При использовании осязательных моделей следует так подобрать уравнения, чтобы система имела целочисленное решение. Этим будет обеспечена возможность осязательного определения решения.

Пусть . Решив систему уравнений, найдём координаты точки пересечения прямых: .

Теперь следует прикрепить прямые к плоскости и убедиться, что они пересекаются в найденной точке. Найдём для каждой прямой по две точки, через которые они проходят. Точку (1; 1) использовать нельзя, потому что в одно отверстие на плоскости нельзя вставить стерженьки двух прямых.

Начнём с прямой y = x. Пусть x = 0. Подставим это значение в уравнение прямой и найдём, что . Одна точка найдена.

Пусть x = 2. Подставим это значение в уравнение и найдём, что . Вторая точка найдена.

Теперь найдём две точки, лежащие на прямой . В частности речь может идти о точках (0; 2) и (2; 0).

Все необходимые точки найдены. Вставим стерженьки первой прямой в отверстия на плоскости, соответствующие точкам (0; 0) и (2; 2), а стерженьки второй прямой в отверстия, соответствующие точкам (0; 2) и (2; 0).

Найдя их точку пересечения, можем убедиться, что это точка (1; 1). Таким образом, система была решена правильно. Задача решена.

2.             Пусть параметры k и b задают уравнение прямой. Кроме того дана точка (х₁; у₁). Прикрепить к плоскости исходную прямую, а также прямую, проходящую через заданную точку, перпендикулярно исходной прямой. Найти координаты точки пересечения двух прямых.

Решение. Пусть . Чтобы прикрепить исходную прямую, нужно найти две точки, через которые проходит исходная прямая. Такими точками могут быть, например, точки (1; 1) и ( 1; 1). Закрепляем первую из прямых в указанных точках на плоскости.

Теперь выведем уравнение перпендикулярной прямой.

Пусть k₁ – угловой коэффициент искомой прямой, b₁ – свободный коэффициент в уравнении искомой прямой. Итак, уравнение искомой прямой имеет вид  + . Для перпендикулярных прямых верно выражение .

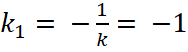Теперь найдём коэффициент b₁. Для этого подставим координаты заданной в условии точки в уравнение . В итоге получаем, что .

Коэффициенты найдены. Уравнение перпендикулярной прямой имеет вид .

Теперь найдём вторую точку, через которую проходит перпендикулярная прямая. Это не должна быть точка пересечения. Пусть x = 1. Подставим это значение в уравнение прямой и получим, что .

Прямая проходит через точки ( 1; 1) и (1; 1). Найдём на модели плоскости отверстия, соответствующие указанным выше точкам, и вставим в них стерженьки перпендикулярной прямой.

Осталось найти точку пересечения прямых. Это можно сделать двумя способами: во-первых, найти её на построенной модели; во-вторых найти её путём решения системы уравнений. Используем оба варианта.

Рассмотрим систему уравнений

 

 

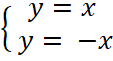
Убедимся, что решениями являются  Значит, прямые пересекаются в точке (0; 0). С помощью модели осязательно убедимся, что это действительно так. Задача решена.

Что касается вопросов, относящихся к моделям декартовой плоскости и прямых, мы ограничимся вышеперечисленными задачами и перейдём к осязательным моделям эллипса. Но ещё в описательном порядке дадим краткие сведения о некоторых моделях, которые не были рассмотрены авторами, поскольку у них отсутствовала материальная модель декартовой плоскости. А это значит, что все задания, связанные с этой моделью можно рассматривать только в умозрительном порядке.

Речь идёт о прямоугольных треугольниках с целочисленной длиной сторон, в вершинах которых расположены стерженьки, позволяющие прикреплять эти треугольники к модели декартовой плоскости. Такие треугольники можно использовать при выводе формулы расстояния между точками на плоскости. Кроме того, поворот такого треугольника на прямой угол позволяет вывести формулу, связывающую угловые коэффициенты перпендикулярных прямых. Возможны и другие многочисленные варианты моделей и их использования.

4.             ОСЯЗАТЕЛЬНЫЕ МОДЕЛИ, СВЯЗАННЫЕ С ИЗУЧЕНИЕМ ЭЛЛИПСОВ

В этом разделе статьи мы будем говорить об осязательных моделях, изготовление которых может быть проведено в бытовых условиях без значительных материальных затрат с использованием инструментов и материалов, доступных в любом домашнем хозяйстве. Здесь неявно просматривается аналогия с известным принципом, утверждающим, что спасение определённой группы людей – дело рук самих этих людей.

Работа над каждой из этих моделей распадается на несколько этапов.

 

1.               Изобретение осязательной модели.

2.               Описание осязательной модели (фактически описание изобретения). В нашем случае все модели, связаны с изучением эллипсов.

3.               Описание технологии создания соответствующей модели.

4.               Описание методики использования этой модели.

5.               Разработка системы заданий, основанных на использовании этой модели.

 

Осязательная модель для изучения определения эллипса (модель 1).

 

Причины разработки модели, связанной с определением эллипса, совершенно очевидны. Дело в том, что стандартным методическим приёмом введения эллипса в курс аналитической геометрии является использование рисунка, на котором изображён процесс построения эллипса с помощью плоскости-картонки, фокусов-гвоздиков, нерастяжимой нити и карандаша (рис. 4).

 

 

Рис. 4.

 

Прежде всего, использование соответствующего рисунка подчёркивает тот факт, что рассмотрение образов, как минимум, полезно. С другой стороны ясно, что в работе со студентами с дефектами зрения использование рисунка невозможно. Именно по этой причине желательно было изобретение осязательной модели. Основная проблема состояла в том, чтобы построить модель, которая позволили бы перемещать нить с бусинкой по границе вырезанного эллипса. При этом вычерчивание эллипса заменяется его ощупыванием.

В итоге такая модель была не только спроектирована, но и реализована с помощью вполне доступных материалов. Приведём инструкцию её изготовления по пунктам и проиллюстрируем процесс создания модели. При этом авторы статьи выражают благодарность Николаю Владимировичу Воронину, который и проделал соответствующие работы.

Порядок создание модели.

 

1.               Приготовить материалы (рис. 5).

 

 

Рис. 5

 

2.               На листе картона провести две перпендикулярных прямых (рис. 6).

 

 

Рис. 6

 

3.               На горизонтальной прямой на расстоянии 8 сантиметров и слева и справа от точки пересечения выделить фокусы Ф1 и Ф2 и сделать в этих точках проколы шилом.

 

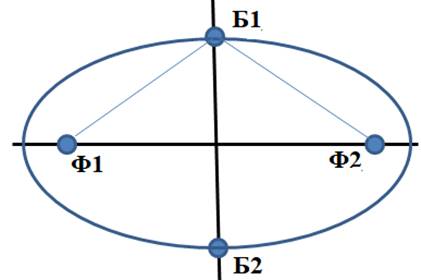
4.               На вертикальной прямой на расстоянии 6 сантиметров и сверху и снизу от точки пересечения выделить две точки Б1 и Б2 (рис. 7).

 

 

Рис. 7

 

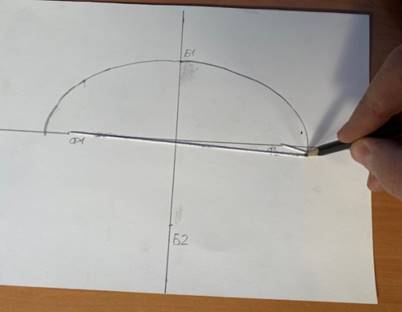
5.               Продеть через отверстия Ф1 и Ф2 суровую нитку. Натянуть её, удерживая в точке Б1. Завязать нить натянутой с тыльной стороны листа картона (рис. 8).

 

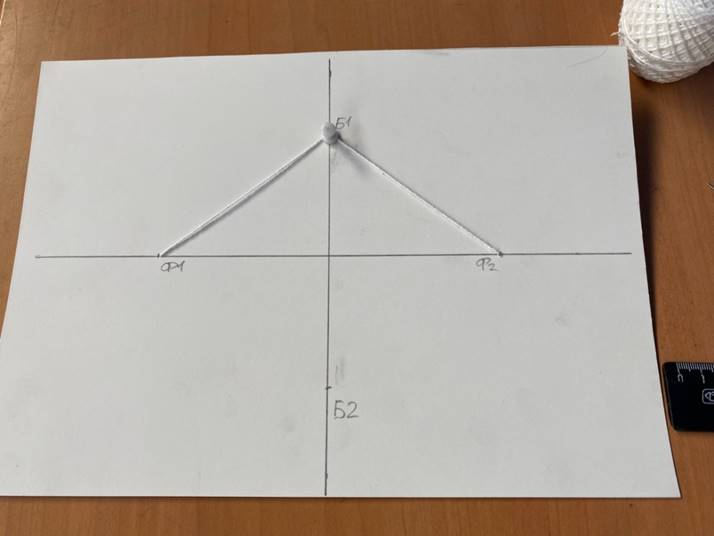
Рис. 8

 

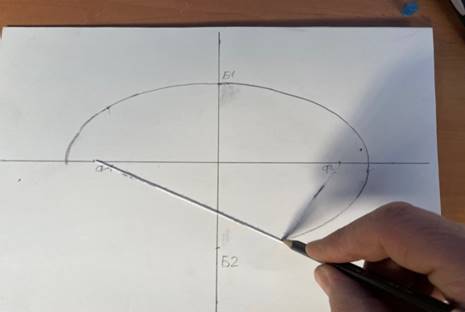
6.               Используя нить, очертить эллипс карандашом (рис. 9).

 

 

 

Рис. 9

 

7.               Вырезать эллипс по линии (рис. 10).

 

 

Рис. 10

8.               Суровую нитку срезать (рис. 11).

 

Рис. 11

9.               Сквозь бусинку продеть две суровых нитки (рис. 12).

 

 

Рис. 12

 

10.           Расположить бусинку на границе эллипса.

 

11.           Продеть одну нитку через Ф1 и Ф2 с лицевой стороны и завязать с тыльной стороны в натянутом состоянии.

 

12.           Продеть вторую нитку через Ф1 и Ф2 с тыльной стороны и завязать с лицевой стороны в натянутом состоянии (рис. 13).

 

 

Рис. 13

 

13.           Модель готова. Нити с двух сторон картонного эллипса держат бусинку на его границе, но так, что вдоль границы можно её перемещать.

 

Отметим, что в ходе создания модели возможны модификации технологии. Так в данном случае бусинка была удачно заменена на обрезок пластмассовой трубочки, что хорошо видно на фотографиях. Возможны и более существенные изменения модели. Например, изготовить её можно из более прочных, чем картон, материалов.

Но уже и на данном этапе модель можно использовать на занятиях по аналитической геометрии. Она достаточно успешно может заменить рисунок для студентов с дефектами зрения.

Осязательная модель для изучения параметров эллипса (модель 2).

 

Порядок создание второй модели

 

1.               Построить и вырезать эллипс с параметрами предыдущей модели, например, вырезать новый эллипс по контуру предыдущей модели.

2.               Далее нужно осязательно выделить фокусы и основные расстояния на модели (рис. 14).

 

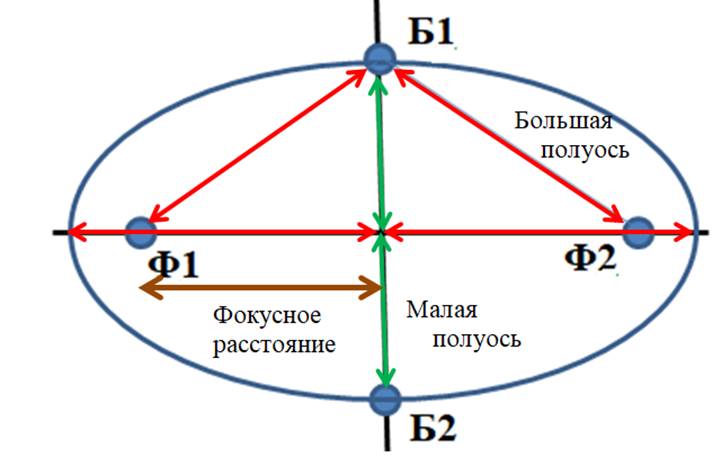
Рис 14.

 

3.               Для выделения фокусов можно наклеить или пришить маленькие пуговички.

4.               Расстояния нужно выделять так, чтобы их можно было осязательно измерить. Для этого нужно нарезать узких полосок и через каждый сантиметр вдоль каждой полоски степлером закрепить скобки. Затем полоски следует наклеить на модель эллипса.

5.               Возможно, полезно наклеить в некоторых местах поясняющие тексты на брайле. Например: «Фокус 1». Или: «Уравнение эллипса ».

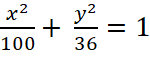6.               Большая полуось имеет длину 10 см, малая полуось – 6 см, фокусное расстояние – 8 см.

 

Отметим, что при реализации материального варианта данной модели выяснилось, что предполагалось наклеить на картонный эллипс слишком много измерительных полосок. В результате возникла идея, состоящая в том, чтобы заменить одну модель по теме «Параметры эллипса» двумя или более её вариантами. На одном варианте можно с помощью осязания определить длину большей полуоси эллипса и расстояние между фокусами. На другом варианте модели, представляющей точно такой же картонный эллипс можно с помощью осязания определить длину меньшей полуоси эллипса. Приведём фотографию первого из вариантов модели (рис. 15).

 

 

Рис. 15

 

Обратим внимание читателя на тот факт, что на модель наклеены брайлевские буквы, отмечающие фокусы эллипса.

Кроме того, при создании модели возникли технические проблемы, связанные с изготовлением «линеек» с помощью степлера. Была разработана другая технология, основанная на использовании скотча (рис. 16).

 

 

Рис. 16

 

Ситуация, связанная с доработкой и переработкой моделей, характерна для предлагаемого в статье проекта.

 

Эллипс – сжатая окружность (модель 3)

 

Порядок создание третьей модели

 

1.               На первом листе картона провести две перпендикулярных прямых.

2.               Провести окружность радиуса 10 сантиметров с центром в точке пересечения этих прямых.

3.               Вырезать окружность.

4.               На втором листе картона провести две перпендикулярных прямых.

5.               На вертикальной прямой на расстоянии 5 сантиметров и сверху и снизу от точки пересечения выделить две точки В1 и В2.

6.               На горизонтальной прямой сделать засечки Ф1 и Ф2 циркулем из центра В1 радиусом 10 сантиметров.

7.               Продеть через отверстия Ф1 и Ф2 суровую нитку. Натянуть её, удерживая в точке В1. Завязать нить натянутой с тыльной стороны листа картона.

8.               Используя нить, очертить эллипс карандашом.

9.               Вырезать эллипс по линии.

10.           Суровую нитку срезать.

11.           Наклеить на окружность эллипс (рис. 17).

 

 

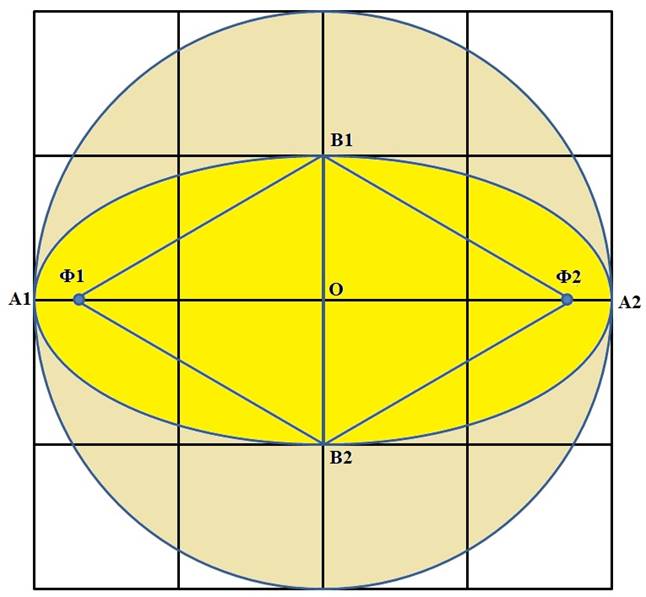
Рис. 17

 

12.           Наклеить вертикальные полоски с насечками от границы круга до горизонтального диаметра, с помощью которых на ощупь можно убедиться, что высота круга всюду ровно в два раза больше высоты эллипса.

 

Сопряжённые диаметры (модель 4).

 

Порядок создание четвёртой модели

 

1.               Провести все работы, как это было сделано в предыдущей модели, с пункта 1 до пункта 11. Вертикальные полоски наклеивать не нужно.

2.               Провести два перпендикулярных диаметра окружности АВ и CD.

3.               Провести от окружности до эллипса вертикальные отрезки АА1, ВВ1, СС1 и DD1.

4.               Провести сопряжённые диаметры А1В1 и С1D1.

5.               Прошив суровыми нитями, сделать отрезки АВ, CD, А1В1, С1D1, АА1, ВВ1, СС1 и DD1 осязаемыми (рис. 18).

 

 

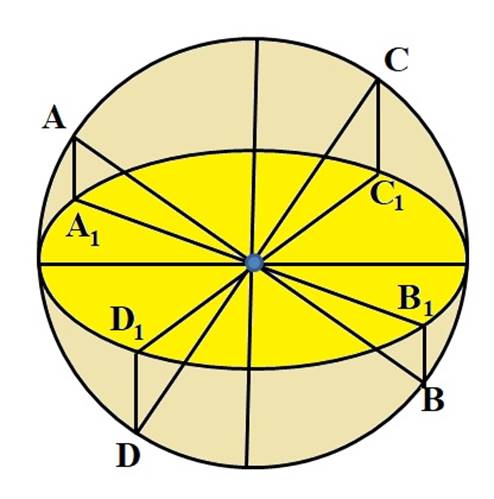
Рис. 18

 

ЗАКЛЮЧЕНИЕ

Данная статья посвящена разработке осязательных моделей предназначенных для обучения математике студентов с дефектами зрения. Более конкретно речь идёт об изучении аналитической геометрии.

Авторами разработано несколько осязательных моделей математических объектов, связанных с тематикой аналитической геометрии. Разработка каждой модели включала в себя изобретение модели, а также создание технологической карты, описывающей процесс реализации модели, как материального объекта. В принципе возможно и промышленное изготовление соответствующих моделей по типу традиционных линеек и лекал.

Однако в ходе работы постепенно был сделан акцент на разработку осязательных моделей, которые можно изготовить в домашних условиях. В статье приведены фотографии, фиксирующие этапы создания подобных моделей.

Авторы планируют продолжить свою работу и надеются, что их деятельность вызовет интерес у преподавателей высшей математики и студентов, изучающих математику.

 

1. Степанов М.Е. Из опыта работы в области тифлопедагогики // Моделирование и анализ данных. 2017. Том 7. № 1. С. 42–53.
2. Куланин Е.Д., Нгуен В.К., Степанов М.Е. Осязаемая предметность с компьютерной поддержкой // Моделирование и анализ данных. 2019. Том 9. № 4. С. 145–156. doi:10.17759/mda.2019090412
3. Куланин Е.Д., Степанов М.Е., Панфилов А.Д., Потонышев И.С. Системный подход к методике тифлопедагогики на примере задач математического анализа  // Моделирование и анализ данных. 2022. Том 12. № 2. (в печати)
4. Куланин Е.Д., Степанов М.Е., Нуркаева И.М. Роль образного мышления в научном мышлении // Моделирование и анализ данных. 2020. Том 10. № 2. С. 110–128. doi:10.17759/mda.2020100209

PlumX

Метрики публикации