О визуализации решений некоторых экстремальных задач

В статье обсуждается задача нахождения прямой на плоскости, сумма квадратов расстояний до которой от n данных точек этой плоскости будет наименьшей. Показывается, как свести эту задачу к решению аналогичной задачи для трех точек, решением которой служит прямая, содержащая большую ось эллипса Штейнера треугольника с вершинами в этих точках. Высказывается также гипотеза о связи рассматриваемой тематики с задачей об областях притяжения в теории фракталов.

1. ВВЕДЕНИЕ.

Настоящей заметкой мы продолжаем серию статей [1]-[4], посвященных решению экстремальных задач.

2. ЗАДАЧА О НАХОЖДЕНИИ МИНИМАЛЬНОЙ ПРЯМОЙ.

Рассмотрим сначала известную задачу нахождения прямой на плоскости, сумма квадратов расстояний до которой от n данных точек этой плоскости будет наименьшей, следуя в основном изложению в [5]. Эта прямая имеет следующий механический смысл: если поместить в данные точки одинаковые массы, то она совпадет с осью, относительно которой полученная система масс имеет наименьший момент инерции.

    Пусть z₁, z₂ , … , z_n  - комплексные числа, соответствующие данным n   точкам на комплексной плоскости. Составим многочлен P(z) = (z – z₁)(z – z₂) … (z – z_n), корнями которого являются числа z₁, z₂, …  z_n . После раскрытия скобок получим P(z) = zⁿ – c₁z^n-1 + c₂z^n-2 –    … (-1) ⁿ c_n ,

где c₁ = z₁ + z₂ + … + z_n , c₂  =  z₁ z₂ +  z₁ z₃ + … +  z_n-1z_n , c_n  =  (-1) ⁿ z₁ z₂  … z_{n .}      

Среднее арифметическое корней   многочлена     обозначим через g:

g = (z₁ + z₂ + … + z_n)/n , откуда  c₁ = z₁ + z₂ + … + z_n = ng  (1)

 и  найдем среднее арифметическое корней   производной   многочлена    P(z):  P^‘(z) =   nz^n-1 – (n-1)c₁z^n-2 + … (-1) ^n-1 c_n-1.

            По теореме Виета сумма корней многочлена   P^‘(z) равна                             (n-1)c₁/n = (n-1)ng/n     =     (n-1)g , т.е. среднее арифметическое корней   z^‘₁, z^‘₂ , … , z^‘_n       многочлена P^‘(z) равно  (z^‘₁+ z^‘₂ + …  +z^‘_n)/(n-1) и, таким образом, средние арифметические корней многочлена P(z) и его производной P^‘(z) совпадают.

Если поместить в данные точки одинаковые массы, то можно сказать, что центры тяжести корней многочлена P(z) и его производной P^‘(z) совпадают.

Понятно, что число g будет единственным корнем (n-1)-ой производной многочлена P(z). Действительно, P^(n-1)(z) = n(n-1) … 2z - c₁(n-1)(n-2) … 2 = 0, откуда после сокращения на (n-1)! = 1*2* … *(n-1) получим nz - c₁  = 0,

z = c₁/n = g. Обозначим через u и v корни многочлена P^(n-2)(z), т.е. корни уравнения n(n-1)z² – 2(n-1) c₁z + 2c₂ = 0.  Тогда по теореме Виета

                                 u + v = 2(n-1)c₁ /(n(n-1)) = 2c₁/n = 2g,   (2)

uv = 2c₂/(n(n-1)) = 2(z₁ z₂ + z₂ z₃ + …  +z_n-1z_n)/(n(n-1)), откуда        

 z₁ z₂ + z₂ z₃ + …  +z_n-1z_n = n(n-1)uv/2.   (3)

   Выразим сумму квадратов корней многочлена P(z) через корни u и v                (n-2)-ой производной этого многочлена:

(z₁ + z₂ + … + z_n) ²    = (z₁²   + z₂²     + … + z²_n) + 2(z₁ z₂ + z₂ z₃ + …  +z_n-1z_n), откуда, учитывая (1) и (3), получим

           z₁²   + z₂²     + … + z²_n   = (z₁ + z₂ + … + z_n) ²    - 2(z₁ z₂ + z₂ z₃ + …  +z_n-1z_n) =  n²g² - n(n-1)uv.  Отсюда легко найти сумму квадратов (z₁ – g) ² + (z₂ – g) ²  + … + (z_n – g) ²   =  z₁²   + z₂²     + … + z²_n   - 2g(z₁ + z₂ + … + z_n) + ng ² =  n²g² - n(n-1)uv – 2g*ng + ng ²  = ng ²(n-1) – n(n -1)uv = n(n -1)(g² – uv).

         Поскольку g = (u + v)/2 (см.(2)), то   g² – uv  =  ((u + v)/2)   - uv =  

   (u² + v² - 2uv)/4 =  (u – v) ² /4, т.е. n(n-1)(g² – uv) =  n(n-1)(u – v) ² /4  и                  

  (z₁ – g) ² + (z₂ – g) ²  + … + (z_n – g) ²   =  n(n-1)(u – v) ² /4. 

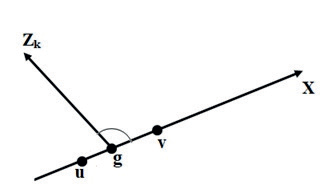
 Обозначим через (x_k ; y_k) координаты комплексного числа   z_k – g (k = 1, 2, …, n) в декартовой системе координат, начало которой совпадает с точкой g, а ось абсцисс проходит через точки u и v (рис.1).  Тогда при делении z_k – g  на x_k + iy_k   из аргумента комплексного числа   z_k – g будет вычитаться угол, образуемый вектором  z_k – g  с осью uv (рис.1), поэтому аргументы чисел

(z_k – g)/(x_k + iy_k)  равны  аргументу числа  v – u.

Рис.1

    Учитывая, что │z_k – g│ = │ x_k + iy_k │, получим:

(z_k – g)/(x_k + iy_k) = … = (z_k – g)/(x_k + iy_k) = (v – u)/(2c),  2c = │v – u│,

откуда (x_k + iy_k) ² = 4с² (z_k – g) ²/(u – v) ² , k = 1, 2, … , n   и                                (x₁ + iy₁) ²  + … + (x_n + iy_n) ²   = 4с²/(u – v) ²((z₁ – g) ² + (z₂ – g) ²  + … + (z_n – g) ²) = (4с²/(u – v) ²)n(n-1)(u – v) ² /4 = n(n-1)c ²                                     

Итак, (x₁ + iy₁) ² + … + (x_n + iy_n) ²   = n(n-1)c ².                                         (3)

Раскрыв скобки в левой части равенства (3), получим:

x₁² - y₁² + … + x_n² - y_n² + 2i(x₁y₁ + … + x_ny_n)  = n(n-1)c ², а выражение  n(n-1)c ² является действительным числом, то

x₁² -  y₁² + … + x_n² - y_n²  = n(n-1)c ², x₁y₁ + … + x_ny_n = 0.                                           (4)

Учитывая то, что мы приняли g за начало новой системы координат, имеем:

   x₁ + x₂ + … + x_n = 0,           y₁ + y₂ +… + y_n = 0.                                                                (5)

Пусть xcosα +ysinα – p = 0 – нормальное уравнение искомой минимальной прямой, где α – угол между нормалью к прямой и осью абсцисс, р – расстояние от начала координат до этой прямой.

Рис.2

Так как φ – внешний угол прямоугольного треугольника OAB, то φ = π/2 + α (рис.2), откуда α = φ - π/2, cosα =cos(φ - π/2) = sinφ, sinα = sin(φ - π/2) = -sin(π/2 - φ) = -cosφ и, таким образом, нормальное уравнение прямой примет вид

                                        x sinφ - ycosφ – p = 0,                                               (6)                    

где φ – угол между искомой прямой и осью абсцисс uv новой системы координат. Обозначим через d_k   расстояния от точек   z_k   до прямой (6) (k = 1, 2, …, n).  Тогда d_k   =  │x_k sinφ - y_kcosφ – p│и                                                              d₁² + … + d_n² = │x₁ sinφ - y₁cosφ – p│² + … + │x_n sinφ - y_ncosφ – p│²     =

(x₁ sinφ - y₁cosφ – p)² + … + (x_n sinφ - y_ncosφ – p)²   = (x₁²   + … + x_n²) sin²φ  +                    

 (y₁² + … + y_n²) cos²φ + np² – 2(x₁y₁ + … + x_ny_n)sinφcosφ -2psinφ(x₁ + x₂ + … + x_n) + 2pcosφ(y₁ + y₂ +… + y_n). Три последних слагаемых равны нулю, поскольку согласно (4) и (5) x₁y₁ + … + x_ny_n = 0, x₁ + x₂ + … + x_n  =  0,                   y₁ + y₂ +… + y_n = 0.

  Итак, d₁² + … + d_n² = (x₁²   + … + x_n²) sin²φ  + (y₁² + … + y_n²) cos²φ + np²  =

(1/2) (x₁²   + … + x_n²) sin²φ + (1/2) (x₁²   + … + x_n²)(1- cos²φ) + (1/2) (y₁² + … + y_n²) cos²φ +(1/2) (y₁² + … + y_n²) (1 - sin²φ) + np²  = (1/2) (x₁² + y₁² … + x_n² + y_n²) + (1/2) (x₁²   + … + x_n²)(sin²φ - cos²φ) + (1/2) (y₁² + … + y_n²)(cos²φ- sin²φ) + np²  =  (1/2) (x₁² + y₁² … + x_n² + y_n²) - (1/2) (x₁²   + … + x_n²) cos2φ +(1/2)(y₁² + … + y_n²)cos2φ  + np²  =                                                                                                 (1/2) (x₁² + y₁² … + x_n² + y_n²) - (1/2)(x₁² - y₁²  + … + x_n² - y_n²) cos2φ + np²  =                                                                                                 (1/2) (x₁² + y₁² … + x_n² + y_n²) - (1/2)n(n-1)c ²cos2φ + np²  ≥                                       (1/2) (x₁² + y₁² … + x_n² + y_n²) - (1/2)n(n-1)c ², причем равенство в последнем неравенстве достигается только в случае  φ = 0, p = 0 .

     Таким образом, минимальная прямая, т.е. прямая в плоскости n данных точек, для которой сумма расстояний от этих точек является наименьшей, проходит через корни u и v (n-2)-ой производной P^(n-2)(z) многочлена P(z).

   Рассмотрим случай n=3. Тогда первое из соотношений (4), а именно

x₁² -  y₁² + … + x_n² - y_n² = n(n-1)c ² примет вид                                                           x₁² -  y₁² + x₂² -  y₂² + x₃² - y₃²  = 3*2*c ² = 6c ².                                   (7)      

Положим x₁² + x₂² + x₃² = 6a ², а y₁² + y₂² + y₃² = 6b ².                        (8)

Тогда равенство (7) преобразуется в                                                                                  x₁² -  y₁² + x₂² -  y₂² + x₃² - y₃² = (x₁² + x₂² + x₃²) - (y₁² + y₂² + y₃²) =6a ² - 6b ² =

6(a ² - b ²) = 6c ², откуда a ² - b ² = c ², где 2c = │v - u│.                       (9)

Таким образом, фокусы эллипса с уравнением x²/a ² + y²/b ²   = 1,  (10)

где a, b и c определяются равенствами (8) - (9) совпадают с точками u  и v.

Покажем, что середины сторон треугольника АВС, где А(x₁; y₁), В(x₂; y₂),

С(x₃ ; y₃) лежат на этом эллипсе.  Пусть М_a , М_b , М_c  -  середины сторон ВС, СА, АВ треугольника АВС соответственно. Тогда М_a ((x₂ + x₃)/2; (y₂ + y₃)/2),

М_b ((x₁ + x₃)/2; (y₁ + y₃)/2), М_c ((x₁ + x₂)/2; (y₁ + y₂)/2). Поскольку начало выбранной нами системы координат совпадает с центром тяжести треугольника АВС, то x₁ + x₂ + x₃ = 0, y₁ + y₂ + y₃ = 0.                     (11)

Кроме того, с учетом (4), имеем   x₁y₁ + x₂y₂ + x₃y₃ = 0,                  (12)

откуда x₃y₃ = - x₁y₁ - x₂y₂ , но согласно (11) y₃ = - y₁ - y₂   , поэтому                          x₃(-y₁ - y₂) = - x₁y₁ - x₂y₂  или x₃y₁ + x₃y₂ =   x₁y₁ + x₂y₂ ,  x₃y₁ -  x₁y₁ =   x₂y₂  - x₃y₂ ,  y₁(x₃ -  x₁) =  y₂ (x₂ -  x₃) , т.е.  y₁/(x₂ -  x₃) =  y₂/(x₃ -  x₁).

Аналогично, y₂/(x₃ -  x₁) =  y₃/(x₁ -  x₂).  Итак, y₁/(x₂ -  x₃) =  y₂/(x₃ -  x₁) =              y₃/(x₁ -  x₂) = k и  y₁ = k(x₂ -  x₃),  y₂= k(x₃ -  x₁), y₃= k(x₁ -  x₂) .           (13)

Но согласно (8) y₁² + y₂² + y₃² = 6b ², поэтому

k²((x₂ -  x₃)² + (x₃ -  x₁)² + (x₁ -  x₂)²) = 6b ²,

k²(2(x₁² + x₂² + x₃²) -2(x₁x₂ + x₂x₃ + x₁x₃)) = 6b ² .

После возведения в квадрат обеих частей равенства x₁ + x₂ + x₃ = 0 (см.(11)), получим  x₁² + x₂² + x₃² + 2(x₁x₂ + x₂x₃ + x₁x₃) = 0, откуда

2(x₁x₂ + x₂x₃ + x₁x₃) = -x₁² - x₂² - x₃²   и

 k²(2(x₁² + x₂² + x₃²) -2(x₁x₂ + x₂x₃ + x₁x₃)) = k²(2(x₁² + x₂² + x₃²) + x₁² + x₂² + x₃²) = 3k²(x₁² + x₂² + x₃²) = 3k² *6a ² = 6b ², т.е. 3k²a ² = 6b ², k² = b ²/3a ².         (14)

Найдем значение выражения x₁²/a ² + y₁²/b ², учитывая (13) и (14):

x₁²/a ² + y₁²/b ² = x₁²/a ² + k²(x₂ -  x₃)² /b ² = x₁²/a² + b²(x₂ -  x₃)² /3a²b ² = (3x₁² +(x₂ -  x₃)²)/3a² = (2x₁² + x₁² + (x₂ -  x₃)²)/3a² = (2x₁² + (-x₂ -  x₃)² + (x₂ -  x₃)²)/3a² = 2(x₁² + x₂² + x₃²)/3a² = 2*6a²/3a² = 4.         Итак, x₁²/a ² + y₁²/b ² = 4.                       (15)                                                                      

   Подставим теперь в уравнение (10) координаты точки М_a ((x₂ + x₃)/2; (y₂ + y₃)/2), заменив x₂ + x₃   и   y₂ + y₃   на -x₁  и  -  y₁  соответственно (см. (11) и (15)):  (-x₁/2) ²/a² + (-y₁/2) ²/b² = (1/4)(x₁²/a² + y₁² /b²) = (1/4)*4 = 1.

   Таким образом, координаты точки М_a удовлетворяют уравнению (10), т.е. точка М_a лежит на этом эллипсе. Точно так же можно убедиться в том, что и середины М_b и М_c сторон АС и АВ тоже лежат на эллипсе (10) с центром в центре тяжести треугольника АВС и фокусами в точках u и v, совпадающих с корнями производной кубического многочлена, корнями которого являются вершины треугольника АВС. Поскольку любой треугольник можно перевести аффинным преобразованием в правильный треугольник, то при таком преобразовании центр тяжести треугольника АВС перейдёт в центр правильного треугольника, а середины сторон треугольника АВС – в середины сторон правильного треугольника, а наш эллипс – во вписанную окружность правильного треугольника. Итак, рассматриваемый эллипс касается сторон треугольника АВС в их серединах. Такой эллипс называется вписанным эллипсом Штейнера. Прямая, проходящая через фокусы эллипса Штейнера, и дает решение задачи о минимизации суммы квадратов расстояний от вершин треугольника до произвольной прямой в плоскости этого треугольника. В общем случае эта минимальная прямая наклонена как к сторонам треугольника, так и к осям системы координат.

Приведем  теперь  определение эллипса Штейнера, вернее двух эллипсов Штейнера – вписанного и описанного.

Пусть заданы правильный треугольник А₀В₀С₀ и произвольный треугольник АВС. Существует аффинное преобразование, которое переводит вершины первого треугольника в соответствующие вершины второго. Образ вписанной в правильный треугольник окружности называется вписанным эллипсом Штейнера. Образ описанной вокруг правильного треугольника окружности называется описанным эллипсом Штейнера. Различные задачи, связанные с эллипсами Штейнера, рассматриваются в статье авторов [10].

    Для того, чтобы сделать картинку более наглядной, рассмотрим обратную задачу: пусть дан эллипс. Найти треугольники, для которых прямая, содержащая большую ось этого эллипса является минимальной.

   Выберем систему координат Oxy так, чтобы её начало совпало с центром эллипса, а его фокусы лежали на оси Ox. Тогда координаты точек должны удовлетворять соотношениям (11) - (12): x₁ + x₂ + x₃ = 0, y₁ + y₂ + y₃ = 0,

x₁y₁ + x₂y₂ + x₃y₃ = 0. Легко подобрать следующее целочисленное решение этих уравнений: x₁ = 1, y₁ = 5, x₂ = 2, y₂ = -4, x₃ = -3, y₃ = -1.

   Для того, чтобы координаты середин сторон треугольника АВС также были целочисленными, достаточно удвоить найденные координаты.

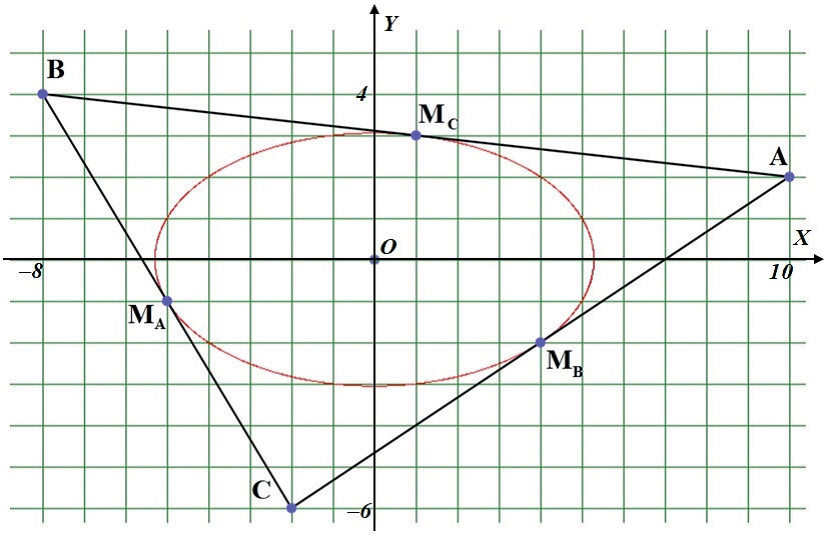
   Тогда А(10; 2), В(-8; 4), С(-2; 6), М_a (-5; -1); М_b(4; -2),  М_с(1; 3).

Треугольник, имеющий такие координаты вершин, вместе с его вписанным эллипсом Штейнера изображен на рис.3.Минимальная прямая этого треугольника совпадает с осью Ox.

Рис.3

То, что ось Ox действительной прямой, легко проверить непосредственно. Сумма квадратов расстояний от вершин А, В, С до оси Ox равна 2² + 4² + 6² = 56. Понятно, что минимальная прямая должна проходить через центр тяжести треугольника АВС, т. е. через начало координат О.  Сумма квадратов расстояний от вершин А, В, С до оси Oy равна 10² + 8² + 2² = 168 > 56. Уравнение любой прямой, проходящей через начало координат и отличной от оси  Oy, имеет вид y = kx,                              поэтому d₁² + d₂² + d₃² =  ((kx₁ - y₁) ² + (kx₂ - y₂) ² + (kx₃ - y₃) ²)/(k² + 1) =

(4/(k² + 1))*((5k - 1) ² + (-4k - 2) ² + (-k + 3) ²) = 4(42k² + 14)/(k² + 1) =

56(3k² + 1)/(k² + 1) = 56(k² + 1 +2k²)/(k² + 1) = 56(k² + 1)/(k² + 1) +                     56*2k²/(k² + 1) = 56 + 112k²/(k² + 1) ≥ 56, причем минимум, равный 56, достигается при k = 0. В этом случае y = 0, т.е. минимальная прямая действительно совпадает с осью Ох.  

3. ПРИМЕНЕНИЯ В МАТЕМАТИЧЕСКОЙ СТАТИСТИКЕ.

  Заметим, что в математической статистике минимальная прямая называется главной компонентой. Основы метода главных компонент (англ.

Principal component analysis, PCA) были заложены знаменитым английским ученым, основателем математической статистики Карлом Пирсоном (1857-1936) в статье [6]. Именно в этой статье и была поставлена задача   нахождения прямой, минимизирующей сумму квадратов расстояний от n данных точек плоскости до этой прямой. В настоящее время метод главных компонент разросся до обширной прикладной дисциплины, занимающейся в том числе и вопросами визуализации данных ([7]-[8]).

4. ГИПОТЕЗА ОТНОСИТЕЛЬНО ПРОБЛЕМЫ А.КЭЛИ ДЛЯ КОМПЛЕКСНЫХ ПОЛИНОМОВ.

 Рассмотрим в заключение некоторую гипотезу относительно проблемы А.Кэли (1821-1895) для комплексных полиномов. В заметке «Комплексная проблема Ньютона-Фурье», опубликованной в 1879г., Кэли предложил применить метод, названный им методом Ньютона-Фурье к комплексным многочленам.

   В действительном случае метод Ньютона   состоит в построении рекуррентной последовательности {x_k-p(x_k)/p^’(x_k), k = 0, 1, 2, …                (16)

    В формулировке Кэли « … задача состоит в разделении плоскости на области так, чтобы, выбрав по желанию точку Р (начальную точку x₀  в (16)), где бы то ни было внутри одной области, мы в конечном счете пришли бы к точке А (равной корню, т.е. р(А) = 0); где бы то ни было внутри другой области  пришли бы к точке В и так далее для каждой из нескольких точек, представляющих корни нашего уравнения.

   В случае квадратного уравнения решение оказывается простым и изящным, но уже следующий сменяющий его случай кубического уравнения,                     по-видимому, представляет значительную трудность [9]. Действительно, для квадратных уравнений данная последовательность всегда сходится к ближайшему корню, за исключением случая, когда начальная точка z₀ лежит на серединном перпендикуляре отрезка с концами, совпадающими с корнями данного квадратного уравнения. В этом случае точки z_к  будут все время оставаться на этом серединном перпендикуляре, совершая хаотическое движение. Для многочленов более высоких степеней, например, кубических, эта задача так и осталась нерешенной, хотя еще в 1879г. Артур Кэли собирался представить решение в следующей публикации, но она, увы, так никогда и не появилась [9].

   Компьютерные эксперименты для кубических многочленов показали, что существуют хорошие по отношению к методу Ньютона многочлены, т.е. такие, для которых почти все начальные точки сходятся к одному из корней, и плохие, для которых начальные точки не сходятся ни к одному из корней уравнения. Однако оказалось, что центр тяжести корней может служить хорошей контрольной точкой: если последовательность с начальной точкой в центре тяжести корней сходится к одному из корней многочлена, то этот многочлен хороший. Если же после достаточно большого числа итераций она не подходит близко ни к одному из корней, то велика вероятность того, что многочлен плохой [9].

    Поскольку минимальная прямая проходит через центр тяжести корней и фокусы эллипса Штейнера, совпадающие с корнями производной кубического многочлена, то естественно предположить, что существует какая-то связь между проблемой Ньютона-Фурье для кубического многочлена и геометрией треугольника с вершинами в корнях этого кубического многочлена. Тогда эта связь будет иметь место и для многочленов высших степеней, так как центр тяжести корней многочлена степени n совпадает с центром тяжести корней его производной (n-3)-го порядка, т.е. с центром тяжести корней кубического многочлена.

   К сожалению, авторы не имеют доступа к быстродействующей вычислительной технике и мониторам с высоким разрешением и, таким образом, не имеют возможности экспериментально проверить эту гипотезу.

1. Куланин Е.Д., Нуркаева И.М. О двух геометрических задачах на экстремум. Математика в школе. 2019. № 4. С. 35-40.
2. Куланин Е.Д., Степанов М. Е., Нуркаева И.М. Пропедевтика решения экстремальных задач в школьном курсе математики. Моделирование и анализ данных.  2019. № 4. С.127-144.