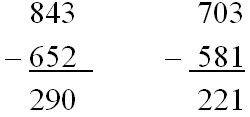Ошибки при освоении математических понятий
Реализация деятельностного подхода в современном российском образовании охватывает как систему общего образования, так и систему подготовки педагогических кадров. Проект модернизации педагогического образования в Российской Федерации послужил импульсом для развития новых направлений психолого-педагогических исследований [Болотов, 2014; Виноградова, 2020; Деятельностный подход в, 2021; Исаев, 2020; Марголис, 2021; Совместная учебная деятельность, 2021]. Разрабатываемая методика развития исходных представлений обучающихся до научных понятий исходит из того, что учитель на уроке не просто фиксирует ошибки, но и анализирует их, выявляет стоящие за ними неправильные представления [Егоренко, 2021; Исаев, 2021; Санина, 2022].
Причины возникновения типичных ошибок по математике в психолого-педагогической литературе рассматриваются рядом авторов. В.А. Далингер выделяет четыре группы: «причины, связанные с психологическими факторами (ослабление психических функций: внимания, памяти, мышления); причины, вытекающие из недостатков учебных программ и учебников; причины, обусловленные несовершенством организации учебного процесса; причины, обусловленные не владением обучающимися на требуемом уровне синтаксисом и семантикой математического языка» [Далингер, 2016]. Н.С. Майкова выделяет следующие причины возникновения ошибок: интерференция навыков, когда формирование нового навыка тормозится уже сложившимся навыком; преобладание ассоциативных связей над смысловыми; игнорирование границ применимости известного способа решения задачи [Майкова, 2008]. О.В. Шереметьева отмечает, что ошибки учеников, допущенные ими в процессе выполнения математических упражнений, могут быть источником диалога на уроке [Шереметьева, 2019]. Р. Эшлок различает неосторожные ошибки, которые мы все совершаем, и неправильные представления о математических идеях и процедурах, которые приводят к появлению типичных ошибок. Он полагает, что в процессе изучения нового понятия ученики сосредотачиваются на своем имеющемся опыте, ищут в нем то общее, что связано с новым понятием, связывают новую информацию с тем, что они уже знают. Однако такое предварительное знание не всегда является правильным, что может привести к ошибочному усвоению нового знания [Ashlock, 2010].
Например, в курсе математики начальной школы рассматриваются задачи с прямыми и косвенными вопросами. Задача с прямым вопросом: «У Васи 8 машинок, а у Димы на 2 меньше, чем у Васи. Сколько машинок у Димы?» Задача с косвенным вопросом: «У Васи 8 машинок, это на 2 меньше, чем у Димы. Сколько машинок у Димы?» Научившись сначала решать задачи с прямыми вопросами, некоторые дети усваивают для себя следующую ассоциацию: если в задаче говорится «на 2 меньше», то нужно вычитать, т. е. задачи со словом «меньше» решаются с помощью вычитания. Когда вводятся задачи с косвенным вопросом, таким детям трудно понять, что для решения второй задачи нужно использовать действие сложения, так как у Димы машинок больше. На протяжении всего предыдущего опыта работы с задачами с прямым вопросом, в которых использовалось слово «меньше», правильным действием было действие вычитания. Таким образом в сознании школьников может возникнуть правило, что решать задачи со словом «меньше» нужно с помощью вычитания. Данное ошибочное представление обучающихся может сохраняться достаточно долго и проявляться затем при решении составных задач.
Арифметические действия традиционно являются одной из основных линий курса «Математика» начального общего образования. Неотъемлемая часть программы по математике — тема «Вычитание». В результате изучения данной темы выпускник начальной школы должен научиться выполнять письменно действие вычитания с многозначными числами в пределах 10000 с использованием таблиц сложения, алгоритма письменного вычитания. С изучением темы непосредственно связано решение текстовых задач, раскрывающих смысл арифметического действия вычитания, и задач, содержащих отношения больше на…, меньше на… Устанавливать зависимость между величинами, представленными в задаче, планировать ход решения задачи, выбирать и объяснять выбор действий — обязательное требование к выпускнику начальной школы.
Обучение приемам письменных вычислений (в столбик) должно базироваться на прочно усвоенных понятиях разрядов чисел и приемах устных вычислений. Переход к письменным вычислениям, в том числе к письменному вычитанию, должен иметь предметную основу, сопровождаться разбором примеров для формирования содержательного обобщения и построением алгоритма выполнения действия с привлечением самих учащихся. Если при изучении приема письменного вычитания акцент будет сделан на формировании навыка пошагового исполнения алгоритма — без установления адекватной связи шагов с математической сущностью выполняемых действий, — то неизбежно будут возникать в большом количестве ошибки.
Как известно, не ошибается тот, кто ничего не делает. Отклонения от правильных действий в процессе обучения — ошибки — неизбежно будут сопровождать любого обучающегося. Однако важно не только указать на ошибку, но и вскрыть возможные причины ее появления.
Рассмотрим основные ошибки обучающихся на материале курса «Математика» начального общего образования на примере темы «Вычитание». Наиболее часто ошибки возникают при реализации алгоритма письменного вычитания (в столбик). Анализ ошибок американских учащихся, проделанный Р. Эшлоком [Ashlock, 2010], соотносится с нашим опытом проверок вычислительных умений российских школьников.
Первый тип ошибок — нарушения в самом алгоритме письменного вычитания.
1. Неверное расположение чисел при записи столбика: нарушено правило записи друг под другом соответствующих разрядов — десятки записаны под сотнями, единицы — под десятками.
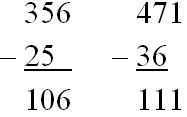
2. Вычитание производится по разрядам, но по принципу «что вычитается». Если из единиц уменьшаемого разряда нельзя вычесть единицы вычитаемого разряда, то вычитаем наоборот.
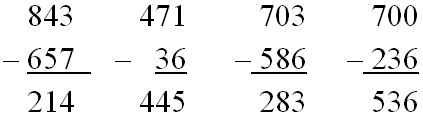
3. Ошибки при вычитании с переходом через разряд: не учитывается уменьшение на 1 единиц старшего разряда, в котором занимали для вычитания единиц младшего разряда.
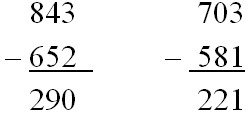
4. Все занимаемые единицы старших разрядов учитываются в разряде сотен (рис. 1 [Ashlock, 2010]).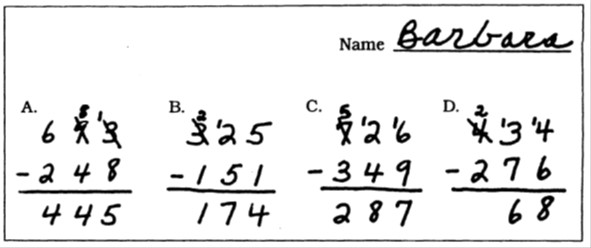
Рис. 1. Шаблон ошибки при выполнении письменного вычитания
5. Вычитание начинается с сотен (слева — направо).
Второй тип ошибок — арифметические ошибки в таблице сложения в пределах 20.
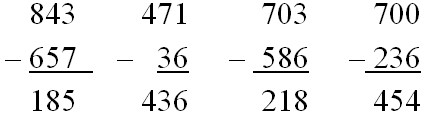
Здесь верно реализуется алгоритм письменного вычитания, но совершаются ошибки вида: 13 – 7 = 5, 11 – 6 = 6, 13 – 6 = 8, 9 – 3 = 5.
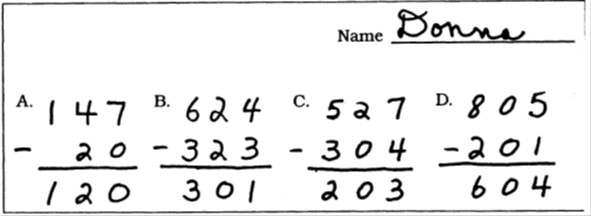
Рис. 2. Пример шаблона ошибки при вычитании нуля из числа.
Здесь также соблюдаются правила алгоритма письменного действия, но ученик ошибается при вычитании нуля из числа: 7 – 0 = 0, 2 – 0 = 0 (рис. 2 [Ashlock, 2010]).
Наконец могут встретиться ошибки такого рода:
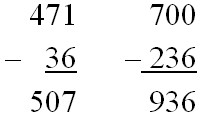
Здесь вместо вычитания выполнено действие сложения.
Приемы работы с ошибками при освоении математических понятий
Методологическим основанием разработки методики развития исходных представлений до научных понятий являются идеи Л.С. Выготского о целостном и едином процессе развития понятий в процессе обучения. Ключевая идея методики работы с исходными представлениями обучающихся при формировании математических понятий — выявление и совместное обсуждение имеющихся у детей наивных представлений, рефлексивное оценивание различных взглядов на изучаемое предметное понятие, согласование мнений и оценок.
Принципиальная позиция Л.С. Выготского о взаимоотношении спонтанных и неспонтанных (научных) понятий состоит в том, что «научные понятия ребенка ... обнаруживают черты не только противоположные спонтанным понятиям, но и черты общие с ними. Граница, разделяющая те и другие понятия, оказывается в высшей степени текучей, переходимой в реальном процессе развития с той и другой стороны неисчислимое количество раз... Развитие спонтанных и научных понятий оказывается взаимно тесно связанными процессами, оказывающими непрерывное воздействие друг на друга» [3, с. 198–199].
Развивающее оценивание.
Исследование компетентности учителей начальной школы в работе над предметными ошибками в начальной школе показало, что исходные представления обучающихся не выступают средством работы над ошибками и отправным пунктом по формированию научных понятий [Исаев, 2023].
Учитель, ориентированный на анализ ошибок с точки зрения стоящих за ними представлений, рассматривает ошибку, по сути, как «окно возможностей» заглянуть в мир предметного мышления ребенка, понять его своеобразие и проложить курс от него к научному знанию. Такой способ оценивания, который можно назвать развивающим, по нашему мнению, является необходимым блоком методики развития исходных представлений обучающихся.
Анализ ошибок учащихся является диагностической оценкой, которая позволяет учителю определить, какие ошибки делают дети и почему. Процесс выявления ошибок учащегося позволяет определить, существует ли шаблон ошибки, т. е. допускает ли ученик постоянно ошибки одного и того же вида. Если шаблон ошибки существует, учитель может выявить неправильные представления или дефицит навыка, чтобы разработать и внедрить индивидуальный план для преодоления затруднений конкретного ученика. Анализ ошибок является эффективным методом выявления шаблонов математических ошибок для любого учащегося, изучающего математику.
Для проведения анализа ошибок следует придерживаться определенной последовательности шагов:
- сбор данных: предложить учащемуся решить не менее 3–5 заданий одного типа;
- определить шаблон ошибок: просмотреть решения учащегося в поисках повторяющихся шаблонов;
- определить причины ошибок: выяснить, почему учащийся делает эти ошибки;
- использовать полученные данные для устранения шаблонов ошибок: определить, какой тип учебной стратегии подойдет лучше всего, чтобы устранить дефицит навыков или недопонимание учащегося.
Типы ошибок и определение причин ошибок.
Обычно математические ошибки учащихся делятся на три большие категории: фактические, процедурные и концептуальные.
- Фактические ошибки — это ошибки, вызванные отсутствием фактической информации (например, словарный запас, идентификация цифр).
- Процедурные ошибки — это ошибки, вызванные неправильным выполнением шагов в математическом алгоритме (например, расстановка цифр в десятичной записи числа).
- Концептуальные ошибки — это ошибки, вызванные неправильными представлениями или неправильным пониманием основополагающих принципов и идей, связанных с математическим понятием, с решаемым математическим заданием (например, взаимосвязь между числами, характеристиками и свойствами фигур) [Санина, 2021; Brown].
Другой причиной появления ошибок может быть проблема ограниченного словарного запаса учащихся. Учащиеся считают математические задания более сложными, если они сформулированы в виде текста, а не в виде числовых выражений. Дети могут неправильно решать текстовые задачи из-за фактических, процедурных или концептуальных ошибок, однако мы можем столкнуться с дополнительными трудностями при решении текстовых задач, многие из которых связаны с дефицитом навыков чтения.
Например, учащийся может не понимать значения математических терминов, таких как сумма, произведение, периметр, площадь. Из-за низкого навыка чтения ученик может испытывать трудность при чтении сложных предложений, поэтому ему будет сложно понять, о чем его спрашивают в задаче. Может сказаться неспособность идентифицировать существенную информацию в общем тексте задачи. Учащемуся будет трудно определить, какая часть информации актуальна и имеет отношение к решению задачи. Учащийся может иметь ограниченный опыт работы с контекстом, в котором разворачивается сюжет задачи.
Приведенная ниже задача иллюстрирует, с какими трудностями может столкнуться школьник.
Задача. «Илья хотел бы купить новый 21-скоростной велосипед. Велосипед стоит 11976 рублей. Илья получил 2500 рублей на свой день рождения. Он также проработал 3 месяца прошлым летом и заработал 5950 рублей. Найдите разность между стоимостью велосипеда и суммой денег, которая есть у Ильи».
В дополнение к неправильному решению этой текстовой задачи из-за фактических, процедурных или концептуальных ошибок ученик может столкнуться с трудностями по причинам, связанным с дефицитом навыков чтения:
- ограниченный словарный запас — ученик может быть не знаком с термином «разность»;
- ограниченные навыки чтения — ученик может столкнуться с трудностями в последнем предложении задачи из-за его сложной структуры. Если ученик не понимает часть слов (например, получил, заработал), это может помешать ему решить задачу;
- неспособность идентифицировать существенную информацию — ученик может обратить внимание на несущественную информацию, такую как тип велосипеда или количество месяцев, в течение которых Илья работал, и, следовательно, решить задачу неправильно;
- отсутствие предварительных знаний — у ученика могут быть ограниченные знания о процессе совершения покупок;
- неспособность перевести информацию в математическое выражение — у ученика могут возникнуть трудности с определением, какие операции выполнять с какими числами. Эта ситуация может усугубиться в случаях, связанных с задачами, решение которых осуществляется в несколько действий.
Определение причины ошибок — это процесс, с помощью которого учителя выясняют, почему ученик совершает определенного типа ошибки. Обычно ошибки ученика не случайны; они часто основаны на неверных систематически применяемых алгоритмах. Иногда определить причину ошибки оказывается труднее. В этих случаях можно использовать одну или несколько из следующих стратегий.
Проведите собеседование с учеником. Иногда непонятно, почему ученик совершает тот или иной тип ошибки. Например, учителю может быть сложно отличить процедурные ошибки от концептуальных. По этой причине может быть полезно попросить учащегося рассказать о своем процессе решения задачи. Знание, о чем думает ученик, когда решает задачу, может быть богатым источником информации о том, что он делает правильно, а что не понимает. Учитель может сказать ученику: «Покажи мне, как ты получил этот ответ». Еще одна причина для учителя провести собеседование с учеником — необходимость убедиться, что у него есть необходимые навыки для решения задачи.
Понаблюдайте за учеником — ученик также может раскрывать информацию невербальными средствами. Это может включать жесты, паузы, признаки разочарования и разговор с самим собой. Учитель может использовать информацию этого типа, чтобы определить, в какой момент при решении задачи учащийся испытывает трудности или разочарование. Это также может помочь учителю определить, какой алгоритм или набор правил применяет ученик и почему.
Устранение шаблонов ошибок.
Устранение шаблонов ошибок — это процесс организации обучения, который фокусируется на конкретной ошибке учащегося. Здесь важно учитывать следующие аспекты:
- учащиеся будут продолжать совершать процедурные ошибки, если они не получат целенаправленной поддержки по устранению этих ошибок. Простая тренировка на большом количестве упражнений, как правило, неэффективна для решения данной проблемы;
- проводя анализ ошибок, учитель может выявить конкретные непонимания или оплошности, а не обучать заново всему умению;
- было показано, что без вмешательства учащиеся продолжают применять те же шаблоны ошибок и год спустя;
- устранение концептуальных ошибок учащегося может потребовать использования конкретных или визуальных представлений, а также значительного переобучения. Учащиеся могут использовать предметную основу для решения задач, в которых они испытывают затруднения;
- простого обучения формуле или шагам алгоритма для решения математической задачи, как правило, недостаточно, чтобы помочь учащимся получить концептуальное понимание [Brown].
После того как учитель определит, какие типы ошибок допускает учащийся, он может устранить ошибку, используя следующие приемы.
Обсудите ошибку с учеником: после того как учитель опросил ученика и изучил результаты работы, учитель должен кратко описать ошибку ученика и объяснить, что они будут работать вместе, чтобы исправить ее.
Обеспечьте эффективное обучение для устранения конкретной ошибки ученика: учитель должен ориентироваться на конкретную ошибку ученика, а не переучивать, как работать с этим типом задач в целом. Например, если ошибка ученика связана с тем, что он не переносит единицы в следующий разряд в письменном сложении, учитель должен сосредоточиться на том, в каком именно месте алгоритма ученик допускает ошибку. Учитель должен точно указать конкретный шаг алгоритма, чтобы сосредоточиться на ошибке и помочь ученику понять, что он делает неправильно. Простое повторное преподавание урока не гарантирует, что ученик поймет ошибку и освоит правильное решение задачи.
Учитывая тип ошибки, учитель должен выбрать эффективную стратегию ее устранения. Тип обучения, который учитель использует для исправления концептуальных ошибок, скорее всего, будет отличаться от того, который используется для устранения фактических или процедурных ошибок. Простое обучение формуле или шагам алгоритма для решения математической задачи не поможет ученику получить концептуальное понимание.
Используйте конкретные объекты, которые помогут учащимся развить концептуальное понимание математического материала. Эти объекты помогают учащемуся представить математическую идею, которую он пытается усвоить, или проблему, которую он пытается решить. Важно, чтобы учитель четко обозначил связь между конкретным объектом и изучаемым абстрактным понятием. После того как учащийся получит базовое представление о математическом понятии, конкретные объекты должны быть заменены визуальными представлениями. Цель состоит в том, чтобы ученик в конечном итоге понял и применил понятие с помощью цифр и символов.
Квазиисследование и полилог.
Следующие два важных взаимосвязанных блока методики развития исходных представлений обучающихся до научных понятий — квазиисследование и полилог.
Первый из них предполагает организацию квазиисследовательской деятельности обучающихся, направленной на выявление ограничений исходных представлений в рамках специально организованных лабораторных и экспериментальных ситуаций со структурированной поддержкой и организацией этой деятельности со стороны учителя. Вторым блоком методики является организация учебной дискуссии в классе (полилога), в которой участвуют все обучающиеся. Целью такой дискуссии является экстериоризация исходных представлений обучающихся об изучаемом объекте. Задачей учителя в рамках этого этапа работы является организация сопоставления различных исходных представлений и помощь в выявлении различий между ними. На уроках математики часто возникают ситуации, когда квазиисследовательская деятельность приводит учащихся к необходимости обосновать свою точку зрения, что и будет являться предметной основой учебной дискуссии. Либо наоборот — сопоставление различных точек зрения учащихся, необходимость проверить выдвигаемые гипотезы — может приводить к организации квазиисследовательской деятельности [4, 9].
В.А. Львовский отмечает важность перевода учителя в задачную форму ведения урока, предусматривающую создание проблемной ситуации, организацию дискуссии, запуск детского действия по поиску решения задачи [Львовский, 2021].
Умение учителя создать проблемную ситуацию — непростая задача, но еще более сложной задачей является умение учителя работать с гипотезами детей. Приведем в качестве примера описание фрагмента урока во втором классе по теме «Письменный прием сложения двузначных чисел с переходом через разряд вида 37 + 25».
На этапе постановки задачи классу было предложено выполнить сложение чисел 37 и 25. В результате были получены четыре разных ответа: 512, 62, 102, 52. Какие варианты реакции на это событие есть у учителя? Возникшая на уроке проблемная ситуация, наличие полученных ответов говорит о том, что учителю удалось своевременно и правильно поставить перед детьми задачу. В этот момент урока как раз и следует столкнуть разные мнения детей друг с другом, выслушать рассуждения о возможных способах действия, прийти при этом в учебной дискуссии к пониманию правильного алгоритма действия, дать возможность учащимся развить свою познавательную инициативу и, вместе с этим, дать возможность трансформации исходных представлений в более полные представления.
Посмотрим, что говорит и как действует учитель: «Достаточно ответов, которые мы получили. Выражения новые. Мы такие выражения с вами решали? Не решали. И, конечно, ответы получились у всех разные. Как определить — правильно мы решили? Какого вида это выражение? Также записывается в столбик. Что нового вы увидели в этом выражении?» Далее учитель фиксирует, что перед нами новый вид выражений — с переходом через разряд и предлагает детям по готовой записи решенного в столбик примера 74 + 17 = 91 объяснить, как здесь рассуждали, чтобы получить правильный ответ. В погоне за экономией времени на уроке учитель игнорирует детские высказывания, торопясь самолично объявить правильное решение, беря на себя инициативу в поиске способа действия, выдавая, по сути, готовый образец способа решения. Г.А. Цукерман метко называет такой способ действия учителя «взрослоцентризм». Она пишет: «В учительском сознании почти отсутствует представление о том, что ребенок всегда имеет собственную ненормативную точку зрения по любому обсуждаемому на уроке вопросу. В детской ошибке обычно усматривают недо-ученность, недо-мыслие, а не возрастное своеобразие мысли, не особое, закономерное для возраста виденье предмета» [Цукерман, 1990, с.19].
Адекватным с точки зрения развития исходных представлений обучающихся могло бы быть развертывание экспериментальной ситуации в виде моделирования действия сложения на основе счетных единиц. Покажем, как это можно сделать на примере аналогичной темы «Вычитание с переходом через разряд».
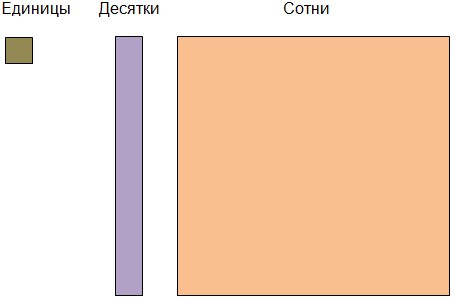
В качестве предметной основы можно использовать набор счетных единиц в виде, представленном на рис. 3.
Здесь единица каждого разряда изображается прямоугольником (квадратом) так, что десяток содержит 10 единиц, сотня содержит 10 десятков. Такой набор счетных единиц нетрудно сделать в бумажном или электронном виде для демонстрации на классной доске, в том числе интерактивной, а также для работы в парах (группах) на рабочих местах.
Работа с таким набором счетных единиц может происходить постоянно, начиная с появления двузначного числа. Систематическое использование подобной модели, на наш взгляд, не должно приводить к трудности установления связи между конкретным объектом (набором счетных единиц) и изучаемым абстрактным понятием (числом). Действия сложения и вычитания удобно и естественно демонстрировать с помощью данного набора.
Например, требуется выполнить вычитание: 134 – 23. Изобразим число 134 (рис. 4).
Чтобы вычесть число 23, уберем из модели 2 десятка и 3 единицы. Получим число 111 (рис. 5).
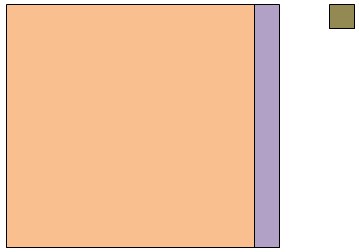
Рис. 5. Результат вычитания — число 111
Теперь попробуем вычесть из 134 число 53. У нас проблема: мы не можем убрать 5 десятков. В обосновании методики развития исходных представлений отмечается, что радикальное изменение исходного и неполного представления, требующее изменения его ключевых характеристик и другого типа обобщения, оказывается возможным не столько в организации непосредственного взаимодействия с изучаемым объектом, сколько в необходимости встраивания индивидуального исследовательского действия в рамки взаимодействия с партнером, т. е. в рамках совместных учебных действий. «Столкновение» не с изучаемым объектом, а с позицией другого обучающегося (партнера по взаимодействию) или необходимость координации своего индивидуального действия в рамках совместно-распределенной деятельности с ним предполагает необходимость аргументации своего способа действия и своего представления об объекте, лежащем в основании такого действия. Такая учебная коммуникация, встроенная в совместное учебное действие, становится эффективным средством развития как индивидуальных действий, так исходных представлений, лежащих в их основании [Деятельностный подход в, 2021].
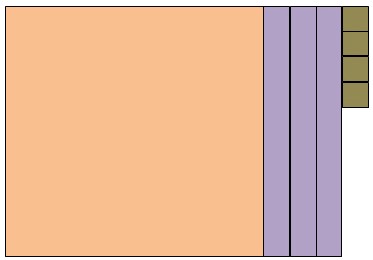
Предполагаемое нами решение задачи состоит в том, чтобы заменить одну сотню на 10 десятков, что и является основой для выполнения действия вычитания с переходом через разряд (рис. 6).
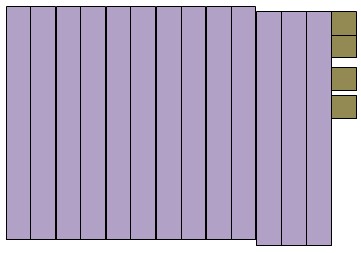
Рис. 6. Представление числа 134 в виде десятков и единиц.
Теперь у нас 13 десятков и 4 единицы. Можно убрать 5 десятков и 3 единицы и получить 8 десятков и 1 единицу, то есть число 81 (рис. 7).
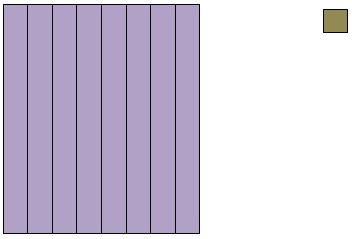
Рис. 7. Результат вычитания — число 81
Представляется, что описываемая проблемная ситуация выполнения вычитания 134 – 53, создает необходимые возможности и для взаимодействия с изучаемым объектом, и для столкновения с позицией другого обучающегося. Для проверки гипотез о правильном ответе можно предложить в парах или группах выполнить вычитание, используя модель счетных единиц, с последующим обсуждением полученных результатов действия.
При таком способе изучения нового материала мы даем обучающимся предметную основу выполняемого действия, к которой они могут обратиться в случае затруднений. И мы создаем условия для развития исходных представлений обучающихся.
Данная статья демонстрирует имеющиеся в педагогической практике приемы работы с исходными математическими представлениями. Мы остановились на способах выявления шаблонов ошибок, допускаемых младшими школьниками при освоении математических понятий, типах ошибок, способах организации развивающего оценивания, квазиисследования и полилога. Дальнейшей задачей нашего исследования является организация опытно-экспериментальной работы по апробации методики развития исходных математических представлений обучающихся до научных понятий в начальной школе.