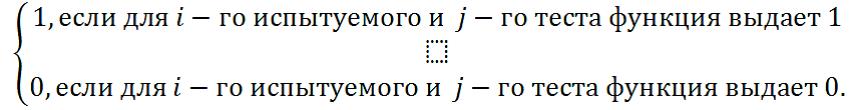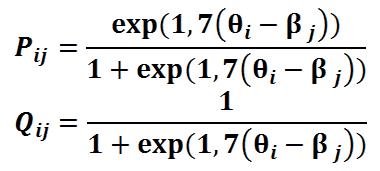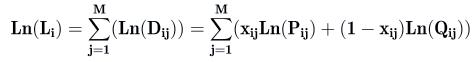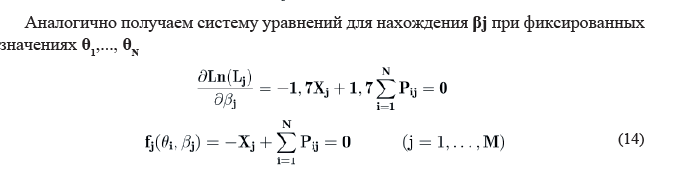Расчет сложностей игровых тестов для системы PLines

В работе предлагается способ вычисления сложностей игровых тестов. Расчеты проводятся для игровой системы PLines. Приводятся краткие сведения о системе PLines.

Введение

В настоящее время бурно развиваются различные средства психологического тестирования. В МГППУ на факультете ИТ разработана игровая система психологического тестирования PLines [5].  За основу взята популярная  игра Lines. Реализовано несколько тестов, воспроизводящих различные закономерности генерации отображения элементов с целью оценить у тестируемых  способности к анализу, планированию действий и рефлексию.

Система PLines функционирует в интернете, результаты тестирования заносятся в базу данных для дальнейшего анализа. С помощью системы PLines многократно проводилось тестирование школьников и студентов.

 Целью данной статьи является предложение подхода к вычислению сложностей разработанных игровых тестов и оценке способностей тестируемых.  Ранее расчеты сложностей заданий и оценки способностей, тестируемых для психологических тестов уже проводились нами [3], [4]. Для этого использовалась методология Раша [1],  [2].

Во всех случаях тестируемые должны были ответить “да” или ”нет” (то есть 1 или 0). Такие ответы часто используются для психологических тестов. В результате получалась матрица из нулей и единиц. К этой матрице применялись методы Раша.  В нашем случае мы получаем  числовые значения  результатов игры. В статье предлагается метод сведения этих числовых значений   к нулям и единицам, что позволило произвести расчеты по ранее опробованным методам. Ниже приводятся краткие сведения об игровых тестах (с примерами),  рассматриваются результаты тестирования и обработка полученных результатов.

Кратко об игре PLines

Система PLines поддерживает несколько различных тестов, количество и порядок следования которых задает администратор-психолог системы.

При запуске каждого теста в системе PLines на окне компьютера отображается квадратное игровое поле из клеток (9 по горизонтали и 9 по вертикали) с тремя шариками разных цветов.  После каждого хода игрока генерируются три новых шарика. Ход состоит из передвижения мышкой шарика с одной позиции на другую. Если игрок выстраивает линию из 5 (или более) шариков одного цвета, то эти шарики сокращаются, а игрок получает очки.  Линия может быть горизонтальной, вертикальной или находиться на диагонали.  Чем больше одновременно сокращается, шариков тем больше очков получает игрок. На Рис 1. изображены возможные фрагменты экрана теста  для закономерностей z103 и z109.

Рис 1. Слева  расположен возможный фрагмент экрана теста  для закономерности z103, справа расположен возможный фрагмент экрана теста  для закономерности z109

Генерация шариков производится по некоторым  закономерностям. Каждому тесту соответствует своя закономерность.

При использовании закономерностей игровое поле делится на две части (верхняя - нижняя или левая - правая).  В этом случае в  одной части шарики располагаются  по указанным  администратором-психологом  закономерности, а на другой шарики появляются в случайном порядке. На выполнение каждого теста дается определенное время.  Результаты заносятся в базу данных.

Обработка результатов

В качестве примера результаты тестирования школьников представлены на Рис 2 и 3.

Строки матриц нумеруем через i (i= 1, ... , N). Столбцы матриц нумеруем через j (j= 1, ... , M).

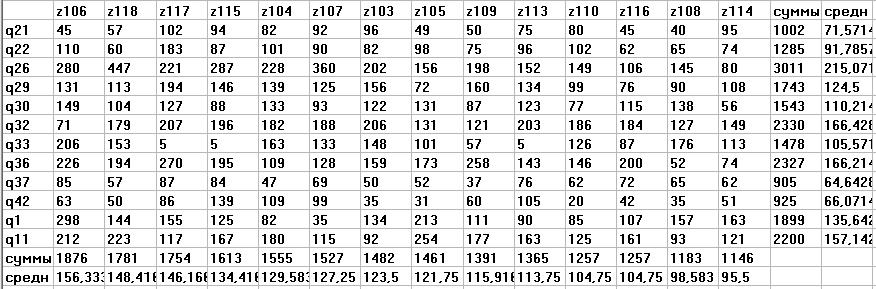
Слева в столбце расположены идентификаторы тестируемых.   В верхней строке расположены  обозначения тестов (или закономерностей). У нас M тестов и N тестируемых.  В предпоследней строке стоят суммы по столбцам. Это набранные очки для каждого теста. В последней строке расположены соответствующие средние значения.

Столбцы отсортированы в порядке убывани средних знаений.  Можно прежположить, что чем больше среднее знаение, тем проще тест (то есть тест z118 проще чем z117).  Но желательно найти велиины, характеризующие сложность  теста без ссылки на набранное оличество очков. Оно может быть разным при каждом тестировании.

Попытаемся свести  к нулям и единицам набранные числовые значения.

Напрашивается желание  присваивать  1, если тестируемый набрал более среднего значени в столбце и 0 в противном случае. Это недостатоно, так как не учитывается взаимосвязь столцов - то, что справа  расположены более трудные тесты.  Желательно прибавлять к среднему некоторое число,  которое будет убавлять колиесто единиц по мере движения по столбцам направо. Важный ворос, какое число прибавлять.  Кроме того, для 1-го теста желательно увеличить число единиц (для стимла).

Пуспь у нас имеется M тестов и SR_j – отсортированные в пордке убывани средние значения для тестов  (SR_j  >= SR_j+1 , j=1,2,..,M).

Пусть  D_j = SR₁  - SR_j , j=2, 3, … , M ,   D₁  = 0    .   

Составим матриу из элементов a_ij  следующим оразом.

Пусть  d_j =  SR_j  /  V  + D_j                (  j=1, 2, … , M ) ,    D₁  = 0      .                                                                                                                       

Здесь V некоторая костанта для увеличения числа единиц  (предлагается V=2).

Обозначим b_ij элементы матрицы для Рис 2. 

Пуспь  a_ij = 1, если b_ij >= d_{j    .}

Пуспь  a_ij = 0, если b_ij < d_{j    .}

Матрицу A из a_ij  возьмем для определения сложностей тестов. К ней можно применить ранее использованную методику вычисления сложностей психологтческих тестов. Такая формула требует улушения и вызывает некоторые сомнения но дает некоторое представление о соотношении сложностей.

Ниже в разделе “Расчет значений сложностей тестов” излагается модифицированна версия этого расчета сложностей.

Обозначим b_ij элементы матрицы для Рис 2. 

Составим матрицу для Рис 2  из элементов a_ij следующим образом:

    Если b_ij  больше d_j  , то берем 1

    В противном случае берем 0

Эти значения также были обработаны по методу Ньютона – Равсона.

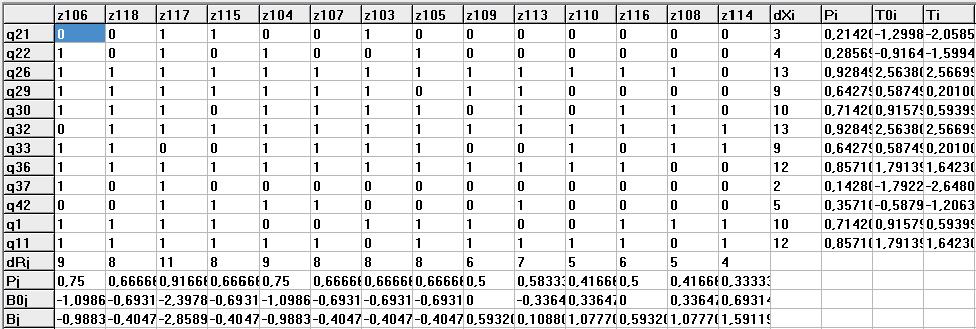
Результаты обработки данных из Рис 2 представлены на  Рис 4. dRj – суммы по столбцам, dXi - суммы по строкам. Pj -  вероятность правильного ответа для теста из  j-го столбца.   Pi  -    доля правильных ответов для i-го испытуемого.

 B0j – начальные значения логитов сложностей. T0i - начальные значения логитов способностей. Bj – вычисленные по “Ньютону” значения логитов сложностей. Ti – вычисленные по “Ньютону” значения логитов способностей.

Рис 2.  Результаты тестирования (очки). Число тестируемых 12

 Идентификаторы тестируемых начинаются с буквы “q”. Число тестов 14 (z118, z117, z107).  Идентификаторы тестов начинаются с буквы “z”.  В предпоследней строке стоят суммы, а в последней строке - стоят средние значения

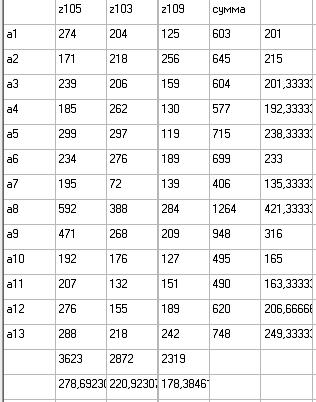
Рис 3.  Результаты тестирования (очки). Число тестируемых 13 (a1-a13)

Число тестов 3 (z105, z103, z109). В предпоследней строке стоят суммы, а в                                    последней строке - стоят средние значения.

Рис 4.  Результаты обработки данных из Рис 2.  Pj – суммы по столбцам, Pi - суммы по строкам. B0j – начальные значения логитов сложностей. T0i - начальные значения логитов способностей. Bj – вычисленные по методу Ньютона – Равсона значения логитов сложностей. Ti – вычисленные по методу Ньютона – Равсона значения логитов способностей

Расчет значений сложностей тестов

Представим вычисление сложностей тестов с помощью концепции Раша в более общем виде.

Пусть имеется M тестов и N испытуемых.  В рассматриваемых тестах испытуемые набирают очки в виде  числовых значений.  Чем меньше в среднем набирают очков, тем тест сложнее. Сортируем столбцы из набранных очков испытуемых по убыванию сумм набранных очков и попытаемся свести вычисления к обычному виду для психологических тестов.

С  помощью средних значений (SR_j) сумм (смотрите выше раздел “Обработка результатов”) и некоторой функции строим матрицу A из нулей и единиц. Один из видов этой функции был рассмотрен выше.  Эта матрица из 0-й и 1-ц представлена на Рис. 4. Она получена с помощью программной обработки данных из Рис. 2.

Обозначим через  элементы матрицы A.  Здесь i  (i = 1,...,N)  дает  номер испытуемого,  j  (j=1,...,M) соответствует номеру теста.

 =  

Получаем матрицу из случайных чисел  x_ij  .

Пусть  - вероятность того, что x_ij  равно 1,     - вероятность того, что x_ij  равно 0.

 Сумма  и   равна 1.

Qij = 1 – Pij

            Обозначим через  логит способности i-го испытуемого, а через  логит  трудности j-го теста.  Наша задача найти  и .  В современной теории тестирования согласно концепции Раша Г. ( Item Response Theory)   и   определяются так:

            Пусть i-й испытуемый в M тестах получил результаты  (j=1,...,M). Тогда  - вероятность получения i-м испытуемым всей последовательности результатов  (j=1,...,M) будет:

Введем обозначения:

p_i – доля единиц в i-й строке  матрицы A (для  i-го испытуемого):   p_i =  X_i  /  M

q_i – доля нулей в i-й строке  матрицы A:   q_i =  1 -  p_i

p_j – доля единиц в j-м столбце  матрицы A (для  j-го испытуемого):   :   p_j =  X_j  /  N

q_j – доля нулей в j-м столбце  матрицы A:   q_j =  1 -   p_j

Приближенные значения оценки способностей испытуемых и трудности заданий теста (их называют логитами) определяются следующим образом [1] :

      = ln (p_i  / q_i )          способности                      (9)

     = ln (q_j  / p_j )          трудности                         (10)

 Верхний индекс 0 здесь поставлен для обозначения того, что они часто используются в качестве начальных значений для вычисления  и .                                                                                                                                  

Вычисление трудности заданий теста и способностей испытуемых с помощью метода максимального правдоподобия

 Более точные значения логитов трудностей тестов и логитов способностей испытуемых  и  вычисляем с помощью метода максимального правдоподобия, используя метод Ньютона-Рафсона.  Точки экстремума для Li и Ln(Li) совпадают. Находим логарифмы  и :

В работе М. Б. Челышкова [1] предлагается решать системы (13, 14) методом

Ньютона-Рафсона, подставляя в них в качестве начальных стандартные значения измеряемых параметров, подсчитанные на основе приближенных значений (9), (10). В работе Ю. М. Неймана, В. А. Хлебникова [2] предлагается находить статистические величины θi и βj только на основе достаточных статистик Xi и Xj, так как это сокращает число неизвестных xij.

Для нахождения корня некоторой функции g(x) = 0 по методу Ньютона-Рафсона (Метод Ньютона, 2013) обычно используется итерационный процесс (15), который начинается с некоего начального приближения x0. Далее:      

Нахождение значений θi и βj производится следующим образом. Сначала вычисляем их приближенные значения (9), (10), затем подсчитываем для них значения по вышеприведенным формулам. Выбираем требуемую погрешность, например, 0,0001. При фиксированных значениях βj подсчитываем по формуле (18) значения θi. Вычисления повторяются до тех пор, пока разность соседних значений не станет меньше значения погрешности по абсолютной величине. Затем повторяем процесс для формулы (19). И так далее… В результате получаем значения трудностей βj для M заданий теста (j= 1, … , M). Проведенные вычисления показали быстрое схождение итераций.

1. Челнышкова М.Б. "Теория и практика конструирования педагогических тестов. Учебное пособие" М. "Логос", 2002.
2. Нейман Ю.М., Хлебников В.А. "Введение в теорию моделирования и параметризации педагогических тестов" М. 2000.
3. Войтов В.К. "Расчет значений сложностей заданий для адаптивного теста интеллекта", Экспериментальная психология, 2013, том 6, №2, с. 120-128.
4. Войтов В.К., Косихин В.В., Ушаков Д.В. Рабочая память как перспективный конструкт когнитивной психологии и методы его измерения // Моделирование и анализ данных. 2015. № 1. С. 57-78.
5. Войтов В.К., Шепелева Е.А., Гаврилова Е.В. , Думин П.Н., Ермаков С.С. Новые средства психологического тестирования  // Моделирование и анализ данных.  2021 № 1  94-108.