Сравнительный анализ эффективности методов построения вполне интерпретируемых линейных регрессионных моделей

Ранее автору удалось свести задачу построения вполне интерпретируемой линейной регрессии, оцениваемой с помощью метода наименьших квадратов, к задаче частично-булевого линейного программирования. В таких моделях знаки оценок соответствуют содержательному смыслу факторов, абсолютные вклады переменных в общую детерминацию существенны, а степень мультиколлинеарности мала. Оптимальное решение сформулированной задачи также может быть найдено методом полного перебора регрессий. Цель статьи заключается в проведении сравнительного анализа эффективности этих двух подходов. Для проведения вычислительных экспериментов использовано 5 наборов реальных статистических данных различных объемов. В результате с помощью пакета LPSolve в разных условиях было решено более 550 различных частично-булевых задач. Параллельно оценена эффективность решения подобных им задач методом полного перебора в пакете Gretl. Во всех экспериментах предложенный нами метод оказался многократно эффективнее метода полного перебора. Самая высокая эффективность была достигнута при решении задач выбора оптимального числа регрессоров из 103 переменных, для решения каждой из которых методом перебора потребовалось бы оценить примерно 2¹⁰³ (10,1 нониллиона) моделей, с чем обычный компьютер не справился бы и за 1000 лет. В LPSolve каждая из этих задач была решена за 32 – 191 секунду. Предложенным методом за приемлемое время удалось обработать выборку данных большого объема, содержащую 40 объясняющих переменных и 515345 наблюдений, что подтверждает независимость его эффективности от объема выборки. Выявлено, что ужесточение в линейных ограничениях задачи требований на мультиколлинеарность и абсолютные вклады переменных практически всегда снижает скорость её решения.

Введение

Процесс построения линейной регрессионной модели условно можно разделить на два этапа: 1) выбор структурной спецификации; 2) оценивание неизвестных параметров регрессии. Выбор структурной спецификации, т.е. математической формы связи между переменными, в линейной модели означает решение задачи отбора  наиболее информативных регрессоров (ОИР) [1,2] из общего их числа  на основе некоторого оптимизационного критерия. Точным методом, гарантирующим оптимальное решение задачи ОИР, считается метод полного перебора [1], алгоритм которого предполагает оценивание  моделей-претендентов. Например, если , , то потребуется оценить 10272278170 моделей. Таким образом, метод полного перебора и самый трудоёмкий из всех методов решения задач ОИР. Если же число отбираемых регрессоров неизвестно, то трудоёмкость метода становится ещё больше, поскольку своей оценки при достаточном объеме выборки  требуют уже  моделей. Самым простым методом оценивания линейных регрессий является метод наименьших квадратов (МНК), в рамках которого разработано множество различных статистических тестов.

Для решения задач ОИР в линейных регрессиях (см., например, [3–11]) в настоящее время успешно применяется аппарат математического программирования, что гораздо эффективнее, чем использование переборных процедур. При этом также гарантируется оптимальность построенной модели. В зарубежной литературе задачи ОИР при использовании МНК принято в основном формулировать в виде задач частично-булевого квадратичного программирования (ЧБКП) [3], скорость решения которых зависит от объема выборки . Результаты анализа научных статей по данной тематике представлены в табл. 1, во втором столбце которой приводятся фамилии учёных и год исследования; в третьем – краткая характеристика решаемой задачи ОИР; в четвёртом – максимальный объем выборки nmax и максимальное число объясняющих переменных lmax , обработанных в результате исследования; в пятом – название решателя задачи математического программирования; в шестом – информация о системе, в которой проводились вычислительные эксперименты.

Таблица 1. Результаты анализа научных статей

По табл. 1 видно, что на сегодняшний день существует множество формулировок задач ОИР в терминах ЧБКП, позволяющих контролировать в процессе решения самые разные характеристики линейных регрессий – качество аппроксимации, мультиколлинеарность, значимость коэффициентов и пр. Также видно, что исследователи избегают решения задач большой размерности, когда объемы выборок более 10000 наблюдений, а число объясняющих переменных более 150 штук. При этом вычислительные эксперименты практически всегда проводятся с использованием дорогостоящих пакетов CPLEX и Gurobi на довольно мощных компьютерах.

В [12] автору удалось свести задачу ОИР в линейной регрессии, оцениваемой с помощью МНК, к задаче частично-булевого линейного программирования (ЧБЛП). Целевой функцией в ней выступает коэффициент детерминации, а количество линейных ограничений, в отличие от формулировок [3–11], не зависит об объема выборки . В дальнейшем формализованная задача дополнилась ограничениями на коэффициенты вздутия дисперсии VIF [13], на t-критерии Стьюдента [14] и пр. На данный момент в [15] приведена самая последняя формулировка задачи ЧБЛП, решение которой приводит к построению вполне интерпретируемой линейной регрессии с оптимальным по коэффициенту детерминации количеством регрессоров, в которой знаки МНК-оценок согласованы со знаками соответствующих коэффициентов корреляции с , абсолютные вклады переменных в общую детерминации не меньше заданного числа , а величины интеркорреляций по модулю не больше заданного числа . Тестирование сформулированной в [15] задачи на реальных выборках большого объема никогда ещё не проводилось.

Цель работы заключается в проведении на основе реальных данных различных объемов сравнительного анализа эффективности решения задачи построения вполне интерпретируемых линейных регрессий методом полного перебора и методом решения специальным образом сформулированной задачи ЧБЛП.

Задача ЧБЛП и программа для её автоматического формирования

Пусть в распоряжении исследователя имеется выборка данных объема  для зависимой (объясняемой) переменной  и  независимых (объясняющих) переменных , , ..., . Составим матрицу коэффициентов интеркорреляций

,

и вектор  корреляций объясняющих переменных с .

Сформулируем задачу ЧБЛП для ОИР в линейной регрессии так, как это сделано в [15]:

,                                                       (1)

,  ,                               (2)

,  ,                                                       (3)

,  ,                                                     (4)

,  ,                                                               (5)

,  ,                                                        (6)

,  ,                           (7)

где , , ...,  – неизвестные параметры линейной регрессии в стандартизованном виде;  – коэффициент детерминации; , , ...,  – бинарные переменные, которые определяются по правилу

 – большое положительное число; ,  – индексные подмножества, элементы которых удовлетворяют условиям  и ;  – абсолютный вклад -й переменной в общую детерминацию ; параметр  – наименьшая величина абсолютных вкладов входящих в модель переменных; параметр  – наибольшая величина коэффициентов интеркорреляций входящих в модель переменных.

Решение задачи ЧБЛП (1) – (7) приводит к построению линейной регрессии с оптимальным по критерию  количеством объясняющих переменных, в которой , , вклады , , а интеркорреляции , , , где  – множество номеров отобранных объясняющих переменных. Заметим, что в построенной регрессии некоторые коэффициенты могут оказаться незначимыми по t-критерию Стьюдента, либо может возникнуть мультиколлинеарность сразу между несколькими переменными. Избежать этого можно, дополнив задачу (1) – (7) линейными ограничениями из работ [13,14].

Как известно, эффективность решения задачи ЧБЛП (1) – (7) зависит от выбора большого положительного числа M: если оно слишком велико, то процесс решения может замедлиться, а если мало, то найденное решение может оказаться неоптимальным. Выбор границ параметра M для задачи (1) – (7) обсуждается в [16]. Сначала определяются параметры ,  для линейных ограничений (3) и (4) по формулам:

,  ,                                                            (8)

где  – коэффициент детерминации регрессии, построенной со всеми  объясняющими переменными. Для удобства можно всегда брать .

Затем находятся параметры ,  для линейных ограничений (2). Для этого нужно решить серию из  задач линейного программирования при :

,                                                       (9)

,  ,                                                          (10)

,  ,                                                         (11)

.                                                                  (12)

После чего аналогично для линейных ограничений (2) находятся параметры , . Для этого решается та же серия задач (9) – (12), но с целевыми функциями на максимум.

И, наконец, в задаче ЧБЛП (1) – (7) ограничения (2) – (4) нужно заменить на следующие:

,  ,                             (13)

,  ,                                                    (14)

,  .                                                    (15)

Формировать задачу ЧБЛП (1), (5) – (7), (13) – (15) по реальной выборке данных для программы-решателя вручную не представляется возможным, особенно, если эта выборка большого объема. Для этого была разработана программа построения вполне интерпретируемых элементарных и неэлементарных квазилинейных регрессионных моделей (ВИнтер-2). Она позволяет в зависимости от выбранных пользователем начальных параметров автоматически формировать для решателя LPSolve IDE задачи ЧБЛП для построения различных, в частности, линейных, регрессионных моделей. Для формирования задачи (1), (5) – (7), (13) – (15) нужно выбрать: 1) число отбираемых регрессоров (при необходимости); 2) число знаков после запятой в действительных числах; 3) параметр ; 4) параметр . Выбор больших чисел M осуществляется автоматически. Сформированная задача представляет собой следующую последовательность блоков: 1) целевая функция (1); 2) левые части двойных неравенств (13); 3) правые части двойных неравенств (13); 4) левые и правые части двойных неравенств (14) и (15), содержащие бинарные переменные; 5) левые и правые части двойных неравенств (14) и (15), не содержащие бинарных переменных; 6) ограничения (6); 7) ограничения (7); 8) ограничения типа b12>=-Inf, указывающие на то, что переменные , , ...,  могут быть не только неотрицательными, но и отрицательными; 9) ограничения типа d10<=1, указывающие верхние границы целочисленных переменных; 10) ограничение типа int d1,d2,d3, указывающее на бинарность целочисленных переменных.

Сформированную задачу нужно вручную открыть в решателе LPSolve, после запуска которого наблюдать за процессом её решения.

Описание данных и их предварительная обработка

Для проведения вычислительных экспериментов были использованы статистические данные, представленные в табл. 2. В третьем столбце указан объем выборки  и количество объясняющих переменных . Как видно по табл. 2, в каждом наборе данных его объем  превосходит число объясняющих переменных . Поэтому предварительно, чтобы убедиться в корректности данных, в пакете Gretl по каждому набору с помощью МНК оценивались модели множественной линейной регрессии. С наборами данных Data1, Data3 и Data5 проблем не возникло, были получены модели без совершенной коллинеарности с коэффициентами детерминации 0.620157, 0.737267 и 0.237001 соответственно.

При построении модели по набору Data2 была выявлена функциональная зависимость:

diffSeTime8 = SeTime6 - SeTime7 + 0.5SeTime8 - 0.5SeTime9 -0.5diffSeTime6,

приводящая к совершенной коллинеарности. При этом установлено, что переменные diffSeTime2 и diffSeTime8 содержат только 2 отличных от нуля значения (-0,001 и 0,001). Поэтому было принято решение исключить эти факторы. В результате осталось 38 объясняющих переменных. В оцененной по новому набору Data2* линейной регрессии нет совершенной  коллинеарности, а её коэффициент детерминации составил 0,819211.

Таблица 2. Описание данных и их характеристики

№	Название (источник); описание; зависимые переменные	(n, l)	Распределение коэффициентов интеркорреляций	Распределение коэффициентов корреляции с y
1	Data1 (пакет Gretl, встроенный файл data7-20.gdt);   данные о зарплатах игроков НБА;   SALARY	(56, 25)
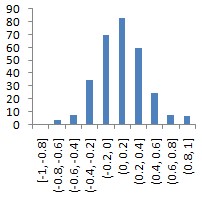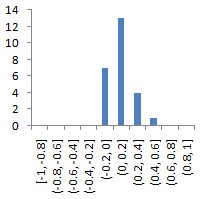2	Data2 (сайт [17]);   данные об элеронах самолёта F16;   Goal	(13750, 40)
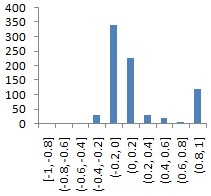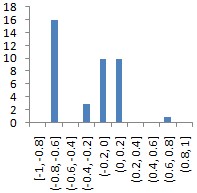3	Data3 (сайт [18]);   данные о критической температуре сверх-проводников;   critical_temp	(21263, 81)
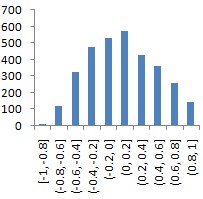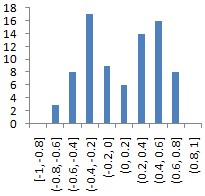4	Data4 (сайт [19]);   данные о стоимостях строитель-ства и ценах продаж квартир в Иране;   V-9, V-10	(372, 103)
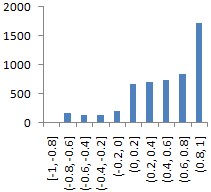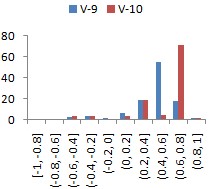5	Data5 (сайт [20]);   данные о годах выпуска песен;   year	(515345, 90)

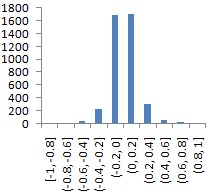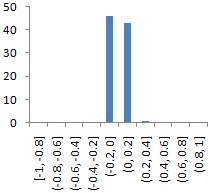Набор данных Data4 содержит две зависимых переменных – V-9 и V-10. Поэтому выборку с зависимой переменной V-9 будем называть Data4a, а с V-10 – Data4b. В модели, оцененной по набору Data4a, выявлена совершенная коллинеарность, поэтому Gretl автоматически исключил 29 переменных. Коэффициент детерминации итоговой модели составил 0,987584. Аналогично, по набору Data4b было исключено 29 факторов, а для итоговой регрессии . Для проведения вычислительных экспериментов было принято решение в наборах Data4a и Data4b оставить список из 103 переменных в полном составе.

Оценка скорости решения задач ОИР методом полного перебора

Получить решение задачи ЧБЛП (1), (5) – (7), (13) – (15) можно также тривиальным способом, организовав полный перебор всех возможных вариантов регрессионных моделей. Для того чтобы была возможность сравнивать эффективность двух этих подходов, требовалось найти статистическую зависимость скорости  решения задач ОИР полным перебором от заданного числа регрессоров . Для этого был разработан специальный скрипт для пакета Gretl, реализующий процедуру отбора ровно  регрессоров в линейной регрессии по следующему алгоритму:

• формируется матрица всех возможных комбинаций регрессоров, содержащая строк и столбцов;
• по выборке находятся корреляционные матрицы и ;
• с помощью матрицы комбинаций в цикле с помощью матриц и находятся стандартизованные оценки линейной регрессии и коэффициенты детерминации ;
• выбирается лучшая модель с наибольшей величиной .

С помощью этого скрипта на персональном компьютере c процессором Intel Core i5-4670 CPU (3.40 GHz) и объемом оперативной памяти 8 GB RAM было проведено два эксперимента – по набору данных Data3 и Data5. Число  задавалось равным 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 20, 25, 30, 35, 36, 37, 40, 45, 50, 55, 58, 64, 70 (при  задача решается практически мгновенно). Для каждого  фиксировалось общее количество обработанных моделей и время решения задачи ОИР (без учёта времени формирования матрицы комбинаций) в секундах. В результате были найдены скорости  (моделей/сек), как отношения общего числа моделей ко времени. Сразу было установлено, что при переходе с  на  в обоих экспериментах произошел солидный скачок скорости  в сторону уменьшения. Поэтому было принято решение строить статистические зависимости отдельно при  и при .

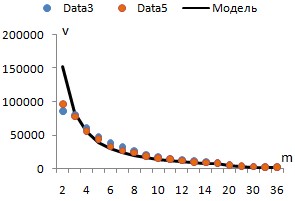
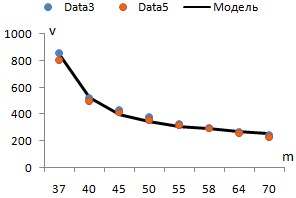
На рис. 1 синими точками указаны скорости, полученные при обработке выборки Data3, а оранжевыми – Data5. Как видно, эти скорости при равных  практически не отличаются. Кроме того, зависимость  от  носит нелинейных характер.

(а)	(б)

Рис. 1. Зависимости скоростей от числа m

Для построения зависимостей в качестве объясняемой переменной была использована средняя скорость . С помощью МНК оценивалась степенная функция  при  и  при . Коэффициенты детерминации оцененных моделей в прологарифмированном виде составили 0,9799 и 0,9856, что подтверждает их высокое качество. Итоговая зависимость средней скорости  решения задач ОИР полным перебором (на конкретном персональном компьютере) имеет вид:

                                         (16)

На рис. 1 черным цветом указаны расчетные по формуле (16) скорости, которые практически совпадают с фактическими.

Вычислительные эксперименты

Вычислительные эксперименты проводились на персональном компьютере c процессором Intel Core i5-4670 CPU (3.40 GHz) и объемом оперативной памяти 8 GB RAM. Решались задачи ЧБЛП (1), (5) – (7), (13) – (15) по наборам данных Data1, Data2*, Data3, Data4a, Data4b и Data5 в зависимости от заданных параметров  и . Параметр  для всех выборок задавался равным от 0,1 до 1 с шагом 0,1. Наименьшее значение параметра  равно 0, а наибольшее  выбиралось так, чтобы при  и  происходил отбор одного или двух регрессоров. Для формирования задач ЧБЛП была использована программа ВИнтер-2, точность действительных чисел – 12 знаков после запятой. Большие числа M в ограничениях (13) – (15) ВИнтер-2 определяет автоматически по формулам (8) при  и как результат решения серий задач линейного программирования типа (9) – (12). Решателем задач ЧБЛП выступает пакет LPSolve IDE с настройками по умолчанию. Лимит времени на решение задачи составляет 1800 секунд (полчаса). Все эксперименты проводились в предположении, что знаки коэффициентов корреляции объясняющих переменных с  согласуются с содержательным смыслом факторов.

Результаты вычислительных экспериментов по данным Data1 представлены в табл. 3.

Таблица 3. Результаты вычислительных экспериментов по набору данных Data1

В табл.3 для каждой пары значений параметров  и  указано количество отобранных переменных , коэффициент детерминации  найденной модели, время  решения задачи в секундах. По этой таблице видно, что, во-первых, во всех 50 случаях получено оптимальное решение в установленный получасовой лимит. Во-вторых, больше всего времени (53,507 с) ушло на решение задачи при  и  (при полном отсутствии требований на вклады переменных и мультиколлинеарность), а меньше всего (0,239 с) – при  и  (при самых жестких требованиях на вклады переменных и мультиколлинеарность). В целом по табл. 3 можно наблюдать, что увеличение  (ужесточение требования на вклады) и уменьшение  (ужесточение требования на мультиколлинеарность) практически всегда снижает время решения задачи.

Решить любую задачу из табл. 3 можно методом полного перебора. Причём, при , 0.001, 0.005, 0.01 для этого пришлось бы оценить  моделей. С помощью формулы (16) установлено, что на это потребовалось бы (без учёта времени на формирование матриц комбинаций и проверки условий) примерно 3206,46 с. Отсюда следует, что эффективность решения задач ОИР представленным способом в LPSolve оказалась в 59,9–8016,1 раз выше, чем методом полного перебора в Gretl. Поскольку значение  для модели со всеми 25 переменными составляет 0,620157, то при  максимальное число регрессоров , поэтому пришлось бы оценить только  моделей, на что потребуется примерно 1232,81 с. В этом случае эффективность решения задач ОИР нашим методом оказалась в 280,2–5158,2 раз выше, чем методом полного перебора.

Результаты вычислительных экспериментов по данным Data2* представлены в табл. 4.

Таблица 4. Результаты вычислительных экспериментов по набору данных Data2*

Как видно, снова во всех 50 случаях получено оптимальное решение в установленный получасовой лимит. И вновь в большинстве случаев чем выше  и ниже , тем меньше время решения задачи. Больше всего времени (365,958 с) ушло на решение задачи при  и , а меньше всего (1,982 с) – при  и . Замечено, что, например, при  с ростом  число отобранных регрессоров может убывать.

При , 0.0005, 0.001, 0.01 методом перебора пришлось бы оценить  (275 миллиардов) моделей, на что потребовалось бы примерно 48138036,2 с или 557 суток непрерывной работы компьютера. Таким образом, эффективность решения задач ОИР представленным способом в LPSolve оказалась в 131540–8731732 раз выше, чем методом полного перебора в Gretl. При  максимальное число регрессоров , поэтому пришлось бы оценить  моделей, на что потребуется примерно 6903730,63 с. В этом случае эффективность решения задач ОИР нашим методом в 1253173–3483214 раз выше, чем методом полного перебора.

Вычислительные эксперименты по набору данных Data3 проводились в четырех разных условиях: 1) прямой порядок объясняющих переменных от 1 до 81; 2) обратный порядок объясняющих переменных от 81 до 1; 3) обратный порядок объясняющих переменных и задача ЧБЛП (1) – (7) с параметрами M=50; 4) обратный порядок объясняющих переменных, задача ЧБЛП (1) – (7) с параметрами M=50 и дополнительными ограничениями на :

,             ,                                              (17)

где  – нижняя граница коэффициента детерминации. Это значение всегда можно брать равным максимальному из коэффициентов детерминации однофакторных линейных регрессий. В данном случае в условиях №4 таблица результатов формировалась построчно слева направо, начиная с нижнего левого угла ( , ). При этом значение  для активных  и  выбиралось равным максимальному из коэффициентов детерминации моделей, полученных на предыдущих шагах при  и . Точность величины  составляла 6 знаков после запятой.

Результаты вычислительных экспериментов по данным Data3 представлены в табл. 5.

Таблица 5. Результаты вычислительных экспериментов по набору данных Data3

В табл. 5 для наглядности серым цветом выделены ячейки, для которых за полчаса либо не доказана оптимальность решения задачи, либо вообще не получено решение. Для сравнения результатов вычислительных экспериментов, проведенных в четырех условиях, была составлена табл. 6. Во втором её столбце для каждого условия указан процент оптимальных решений 50 задач, в третьем – процент задач без решения в установленный лимит времени, в четвертом – общее время решения 50-ти задач, в пятом – среднее время поиска оптимального решения, в шестом – среднее значение  для моделей с доказанной и не доказанной оптимальностью.

Таблица 6. Показатели эффективности решенных по данным Data3 задач в зависимости от условий

По табл. 6 можно сделать следующие выводы.

1. Порядок следования объясняющих переменных в исходной выборке может существенно влиять на скорость решения задачи ЧБЛП. Оказалось, что изменение порядка следования переменных с прямого (от 1 до 81) на обратный (от 81 до 1) увеличило процент оптимальных решений на 22%, снизило процент решений без результата на 2%, уменьшило общее время решения 50-ти задач на 19533 с (примерно на 5,5 часов) и среднее время на поиск оптимального решения на 209,5 с, а также увеличило среднее качество моделей по R2 на 0,007043.
2. На скорость решения задачи ЧБЛП могут существенно влиять выбранные значения больших чисел . Получилось, что по выборке с обратным порядком следования переменных изменение в задаче (1), (5) – (7), (13) – (15) всех больших чисел на уменьшило процент решений без результата на 2%, общее время решения 50-ти задач на 3736,27 с, среднее время на поиск оптимального решения на 109,89. При этом процент оптимальных решений не изменился, а среднее качество моделей по R2 снизилось на 0,000546.
3. Внедрение ограничений (17) может существенно влиять на скорость решения задачи ЧБЛП. Последовательное проведение экспериментов в условиях №4 оказалось самым эффективным. По сравнению с экспериментами в условиях №3 уменьшилось общее время решения 50-ти задач на 743,03 с, среднее время на поиск оптимального решения на 164,23 с, увеличилось среднее качество моделей по R2 на 0,0058. Процент решений без результата не изменился, а процент оптимальных решений снизился на 6% из-за задач при , .

Для сравнения с методом перебора была взяты результаты вычислительных экспериментов (только оптимальные решения), полученные в условиях №3. Тут снова прослеживается снижение времени решения задач при больших  и малых .

При  методом перебора пришлось бы оценить  (2,4 септиллиона) моделей примерно за  с; при  – примерно то же самое; при  –  (2,3 квадриллиона) моделей примерно за  с (7853 года); при  –  (2,1 триллионов) моделей примерно за 144911622 с (4,6 лет); при  –  (3,8 миллиарда) моделей примерно за 151981 с (42,2 часов).

Таким образом, эффективность решения задач ОИР нашим методом в LPSolve при  в  –  раз, при  в  –  раз, при  в 420992349 – 4254439602 раз, при  в 389499,2 – 2838732,6 раз, при  в 515,5 – 3427,4 раз выше, чем методом полного перебора в Gretl. Подтверждают эффективность и дополнительные эксперименты при  и . Эти задачи были решены за 3278,48 с, 7383,34 с, 11866,6 с и 12386,7 с соответственно. Количества отобранных переменных и коэффициенты детерминации построенных моделей оказались следующие: (5, 0.5948), (9, 0.6297), (10, 0.6520) и (11, 0.6543).

Вычислительные эксперименты по набору данных Data4a проводились в двух разных условиях: 1) без ограничений на R2; 2) с ограничениями (17) на R2, . Результаты представлены в табл. 7.

Таблица 7. Результаты вычислительных экспериментов по набору данных Data4a

 По табл. 7 видно, что в обоих условиях процент решений без результата составляет 0%. Оказалось, что введение ограничений на R2 увеличило процент оптимальных решений с 56% до 100%, снизило общее время решения 50-ти задач с 61688,85 с до 4260,19 с (примерно в 14,5 раз) и среднее время на поиск оптимального решения с 788,88 с до 85,2 с (примерно в 9,2 раза), увеличило среднее качество моделей по R2 c 0,824478 до 0,960828.

Для сравнения с методом перебора была взяты результаты вычислительных экспериментов, полученные в условиях №2a. Снова прослеживается снижение времени решения задач при больших  и малых . Но в этот раз оно менее выраженное.

При  методом перебора пришлось бы оценить  (10,1 нониллиона) моделей примерно за  с (без учёта времени на формирование матриц комбинаций и проверки условий); при  – примерно то же самое.

Таким образом, эффективность решения задач ОИР нашим методом в LPSolve в  –  раз выше, чем методом полного перебора в Gretl.

Вычислительные эксперименты по набору данных Data4b проводились в двух разных условиях: 1) без ограничений на R2; 2) с ограничениями (17) на R2, параметр , значение  с шестью знаками после запятой выбиралось так же, как при экспериментировании по выборке Data3 при условиях №4. Результаты представлены в табл. 8.

Таблица 8. Результаты вычислительных экспериментов по набору данных Data4b

 По табл. 8 было установлено, что в условиях №2b процент решений без результата увеличился с 0% до 4%, процент оптимальных решений увеличился с 32% до 82%, общее время решения 50-ти задач уменьшилось с 75279 с до 23360,2 с, среднее время на поиск оптимального решения уменьшилось с 879,9 с до 174,6 с, среднее качество моделей по R2 увеличилось с 0,91034 до 0,957776.

Для сравнения с методом перебора была взяты результаты вычислительных экспериментов, полученные в условиях №2b. Судить о влиянии  и  на время решения задач не правомерно, поскольку все они были решены при разных .

При  методом перебора пришлось бы оценить  моделей примерно за  с; при  – примерно то же самое; при  –  (0,777 октиллиона) моделей примерно за  с; при  –  (0,252 септиллиона) моделей примерно за   с.

Таким образом, эффективность решения задач ОИР нашим методом в LPSolve при  в  –  раз, при  в  –  раз, при  в  –  раз выше, чем методом полного перебора в Gretl.

Вычислительные эксперименты по самому крупному набору данных Data5 предварительно проводились по ненулевым значениям  и низким значениям . В установленные получасовые лимиты были получены следующие результаты: 1) при  и  отобрано 3 регрессора, , оптимальность не доказана; 2) при  и  нет результата; 3) при  и  отобрано 2 регрессора, , оптимальность не доказана; 4) при  и  нет результата.

Таким образом, установленного получасового лимита оказалось недостаточно для решения задач по выборке Data5. Тем не менее, в некоторых случаях довольно быстро получаются близкие к оптимальным, а, возможно, и оптимальные, решения.

Далее было принято решение упорядочить объясняющие переменные по убыванию модулей их коэффициентов корреляции с  и из первых 40 факторов сформировать новую выборку Data5*. Для линейной регрессии со всеми 40 переменными . Результаты вычислительных экспериментов по набору данных Data5* представлены в табл. 9.

Таблица 9. Результаты вычислительных экспериментов по набору данных Data5

 По табл. 9 можно сделать вывод, что оптимальных решений – 84%, решений без результата – 0%, общее время решения 50-ти задач – 41510 с, среднее время на поиск оптимального решения – 645,5 с, среднее качество моделей по R2 – 0,1339. Значения в табл. 9 подтверждают, что с ростом  и уменьшением  скорость решения задач практически всегда возрастает.

При  методом перебора пришлось бы оценить  моделей примерно за 207409219 с (6,57 лет); при  – примерно то же самое; при  –  моделей примерно за 168933865 с (5,35 лет); при  –  моделей примерно за 31076852 с (1 год).

Таким образом, эффективность решения задач ОИР нашим методом в LPSolve при  в 117766 – 7889582 раз, при  в 334967 – 7540007 раз, при  в 76836 – 1479709 раз выше, чем методом полного перебора в Gretl.

Заключение

Подчеркнем основные результаты, полученные в данной работе.

1. Экспериментально доказано, что построение вполне интерпретируемой линейной регрессии предложенным методом, состоящим в решении задачи ЧБЛП (1), (5) – (7), (13) – (15), многократно эффективнее метода полного перебора. Для набора данных Data1 наш подход оказался эффективнее в 59,9 – 8016,1 раз; для Data2* – в 131540 – 8731732 раз; для Data3 – в 515,5 – раз; для Data4a – в –  раз; для Data4b – в  –  раз; для Data5* – в 76836 – 7889582 раз.
2. Среди полученных за получасовой промежуток времени 550-ти решений, представленных в табл. 3, 4, 5, 7, 8, 9, оптимальных оказалось 399 (72,6%), обычных – 130 (23,6%), отсутствующих – 21 (3,8%). Таким образом, за приемлемое время в большинстве случаев были найдены оптимальные или близкие к ним решения.
3. Эффективность предложенного метода не зависит от объема выборки , поэтому удалось обработать набор данных Data5*, содержащий 40 объясняющих переменных и 515345 наблюдений. Так, например, в работах [3-11] зарубежных авторов максимальный объем выборки для решения подобных задач составил всего 9358 наблюдений, т.е. примерно в 55 раз меньше.
4. Замечено, что выбор параметров и может существенно влиять на скорость решения задачи ЧБЛП. Причём, с увеличением  (ужесточение требований на вклады переменных) и уменьшением  (ужесточение требований на мультиколлинеарность) время решения задачи в большинстве случаев снижается, т.е. вполне интерпретируемая линейная регрессия строится быстрее, чем реализуется обычный ОИР без ограничений на  и .
5. Установлено, что на эффективность решения задачи ЧБЛП может существенно влиять порядок следования объясняющих переменных в выборке, параметр M, а также дополнительные ограничения (17) на коэффициент детерминации. Механизм влияния этих и других параметров на скорость решения задачи ЧБЛП требует дальнейших исследований.

1. Стрижов В.В., Крымова Е.А. Методы выбора регрессионных моделей. М.: Вычислительный центр им. А.А. Дородницына РАН, 2010. 60 с.
2. Miller A. Subset selection in regression. CRC Press, 2002.
3. Konno H., Yamamoto R. Choosing the best set of variables in regression analysis using integer programming // Journal of Global Optimization. 2009. Vol. 44. P. 273–282. DOI:10.1007/s10898-008-9323-9.
4. Miyashiro R., Takano Y. Mixed integer second-order cone programming formulations for variable selection in linear regression // European Journal of Operational Research. 2015. Vol. 247. P. 721–731. DOI:10.1016/j.ejor.2015.06.081.
5. Miyashiro R., Takano Y. Subset selection by Mallows’ Cp: A mixed integer programming approach // Expert Systems with Applications. 2015. Vol. 42. P. 325–331. DOI:10.1016/j. eswa.2014.07.056.
6. Park Y.W., Klabjan D. Subset selection for multiple linear regression via optimization // Journal of Global Optimization. 2020. Vol. 77. P. 543–574. DOI:10.1007/s10898-020-00876-1.
7. Tamura R., Kobayashi K., Takano Y., Miyashiro R., Nakata K., Matsui T. Mixed integer quadratic optimization formulations for eliminating multicollinearity based on variance inflation factor // Journal of Global Optimization. 2019. Vol. 73. P. 431–446. DOI:10.1007/s10898-018-0713-3.
8. Tamura R., Kobayashi K., Takano Y., Miyashiro R., Nakata K., Matsui T. Best subset selection for eliminating multicollinearity // Journal of the Operations Research Society of Japan. 2017. Vol. 60(3). P. 321–336. DOI:10.15807/jorsj.60.321.
9. Bertsimas D., Li M.L. Scalable holistic linear regression // Operations Research Letters. 2020. Vol. 48, Is. 3. P. 203–208. DOI:10.1016/j.orl.2020.02.008.
10. Chung S., Park Y.W., Cheong T. A mathematical programming approach for integrated multiple linear regression subset selection and validation // Pattern Recognition. 2020. Vol. 108. DOI:10.1016/j.patcog.2020.107565.
11. Takano Y., Miyashiro R. Best subset selection via cross-validation criterion. Top. 2020. Vol. 28, Is. 2. P. 475–488. DOI: 10.1007/s11750-020-00538-1.
12. Базилевский М.П. Сведение задачи отбора информативных регрессоров при оценивании линейной регрессионной модели по методу наименьших квадратов к задаче частично-булевого линейного программирования // Моделирование, оптимизация и информационные технологии. 2018. Т. 6. № 1 (20). С. 108-117.
13. Базилевский М.П. Отбор информативных регрессоров с учётом мультиколлинеарности между ними в регрессионных моделях как задача частично-булевого линейного программирования // Моделирование, оптимизация и информационные технологии. 2018. Т. 6. № 2 (21). С. 104-118.
14. Базилевский М.П. Отбор значимых по критерию Стьюдента информативных регрессоров в оцениваемых с помощью МНК регрессионных моделях как задача частично-булевого линейного программирования // Вестник Воронежского государственного университета. Серия: Системный анализ и информационные технологии. 2021. № 3. С. 5-16.
15. Базилевский М.П. Формализация процесса отбора информативных регрессоров в линейной регрессии в виде задачи частично-булевого линейного программирования с ограничениями на коэффициенты интеркорреляций // Современные наукоёмкие технологии. 2023. № 8. С. 10-14.
16. Базилевский М.П. Способ определения параметра M в задаче частично-булевого линейного программирования для отбора регрессоров в линейной регрессии // Вестник Технологического университета. 2022. Т. 25. № 2. С. 62-66.
17. Knowledge Extraction based on Evolutionary Learning [Электронный ресурс]. – Режим доступа: https://sci2s.ugr.es/keel/dataset.php?cod=93 (дата обращения 04.10.2023).
18. UCI Machine Learning Repository [Электронный ресурс]. – Режим доступа: https://archive.ics.uci.edu/dataset/464/superconductivty+data (дата обращения 04.10.2023).
19. UCI Machine Learning Repository [Электронный ресурс]. – Режим доступа: https://archive.ics.uci.edu/dataset/437/residential+building+data+set (дата обращения 04.10.2023).
20. UCI Machine Learning Repository [Электронный ресурс]. – Режим доступа: https://archive.ics.uci.edu/dataset/203/yearpredictionmsd (дата обращения 04.10.2023).