Введение
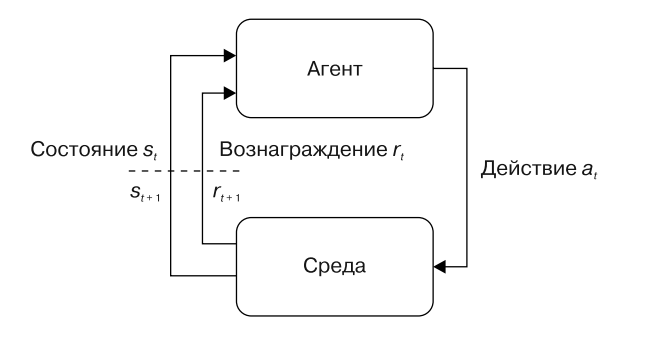
В настоящее время алгоритмы глубокого обучения с подкреплением помогают решать задачи искусственного интеллекта методом проб и ошибок, не обладая априорными знаниями о решаемой задаче. Сам термин подкрепление (reinforcement) обозначает награду или наказание за результат, который может зависеть не только от принятых решений, но и некоторых неподконтрольных факторов. Вместо подачи обучающей выборки на вход алгоритму обучение происходит за счёт взаимодействия с некоторой средой (environment). Под желаемым результатом подразумевается максимизация некоторой скалярной величины, называемой наградой (reward). Саму сущность (систему), которая принимает решения и взаимодействует со средой, принято называть агентом (agent). При взаимодействии агента с миром или средой агенту доступно только некоторое наблюдение (observation) текущего состояния данной среды. Агент взаимодействует со средой посредством действий (actions), которые выбираются благодаря некоторой процедуре. Данную процедуру принято называть стратегией или политикой (policy). Сам процесс взаимодействия агента и среды называется динамикой среды (world dynamics), которая определяет условия, по которым меняются состояния среды во времени и генерируется некоторая награда.
Основываясь на том, что агент взаимодействует со средой, а соответственно, выполняет какие-либо действия благодаря своей стратегии, которая моделируется некоторым распределением, в широкое применение вошло использование глубоких нейронных сетей для аппроксимации данной функции распределения. В связи с прогрессом в области искусственного интеллекта появилось множество новых архитектур нейронных сетей, а именно архитектура сети Transformer, именно она будет использована в данной работе. Благодаря ей стало возможно обрабатывать последовательности векторов и вектор контекста самой последовательности, не теряя при этом входную информацию.
Связь с оптимальным управлением и марковским процессом принятия решений
Буквами s, a, r принято обозначать состояния, действия и награды, буква t используется для идентификации времени. Для объяснения задачи в терминах оптимального управления нужно свести её в рамки лаплассовского детерминизма и определить модель мира [Конспект по обучению]. Это означает, что положение, скорости и ускорения всех атомов вселенной задают её исходное состояние, а изменение этого состояния происходит согласно некоторым дифференциальным уравнениям. Исходя из вышеупомянутых высказываний, систему можно описать:
Поскольку агент обладает некоторой стратегией принятия решений, а соответственно может влиять на среду, то основываясь на уравнении выше можно описать взаимодействие агента со средой следующим образом:
Описываемую задачу можно представить через определение марковской цепи, где переход из состояния в состояние зависит только от текущего момента времени и состояния агента, но не зависит от всей предыдущей истории взаимодействия агента со средой. Таким образом, предложенное свойство Марковости позволяет свести задачу к MDP – Марковскому процессу принятия решений (Markov Decision Process, MDP). Данное определение не проявляется в усложнении задачи, поскольку его легко представить в виде:
где S, A, P – это описание среды, а именно:
S – пространство состояний, множество состояний, в которых в каждый момент времени может находится среда;
A – пространство действий, множество вариантов действий, из которых агент производит свой выбор на каждом шаге;
P – функция перехода, которая задаёт изменение среды после того, как в состоянии s было выбрано действие a;
Описание поставленной задачи и модели мира
Целью данной работы является проверка применимости архитектуры сети Transformer для аппроксимации политики агента и сравнение с полносвязной архитектурой сети в задаче обучения с подкреплением посредством обработки последовательности данных. Идея использования архитектуры сети Transformer основывается на том, что множество алгоритмов обучения с подкреплением страдает от увеличения пространства действий, что прямым образом сказывается на сходимости алгоритма решения. Поэтому использование новой архитектуры сети с возможностью обработки последовательностей позволит уменьшить пространство действий, что приведёт к ускорению сходимости и увеличению суммарной награды.
Задачу можно сформулировать следующим образом. Агенту доступны: вид пространства состояний, вид пространства действий и взаимодействие со средой. Благодаря последнему, агент собирает данные путём выбора некоторого действия, перемещающего его из одного состояния в другое, где совершаемое агентом действие принадлежит некоторой стратегии (политике), которую аппроксимирует нейронная сеть. Требуется определить стратегию агента, максимизирующую суммарную награду на основе его опыта взаимодействия со средой.
Для реализации решения поставленной задачи используется симулятор Mujoco – бесплатный физический движок с открытым исходным кодом, принадлежащий DeepMind. Существует одиннадцать сред Mujoco: Ant, Hopper, Humanoid и др. Для реализации и тестирования поставленной задачи использовалась среда Ant, которая основана на модели мира, представленной Шульманом, Морицем, Левином, Джорданом и Аббилем в работе [High-dimensional continuous control]. Ant – это 3D робот, который состоит из туловища с прикреплёнными к нему четырьмя ногами, где каждая из которых состоит из двух секций. Суть задачи сводится к удержанию роботом равновесия и движения вышеупомянутого вперёд, путём координации его действий с помощью приложения крутящих моментов к каждому шарниру робота. Шарниры находятся на стыках креплений секций ног и соединений самих ног с туловищем.
Таким образом, пространство действий можно представить в виде вектора размерности 8 (Таблица 1), где каждое значение представляет собой крутящий момент, приложенный к шарнирному соединению.
Таблица 1. Пространство действий агента (робота Ant)
|
Индекс |
Действие |
Минимальное значение |
Максимальное значение |
|
0 |
Крутящий момент, приложенный к шарниру между туловищем и задним правым бедром |
-1 |
1 |
|
1 |
Крутящий момент, приложенный к шарниру между двумя секциями задней правой ноги |
-1 |
1 |
|
2 |
Крутящий момент, приложенный к шарниру между туловищем и передним левым бедром |
-1 |
1 |
|
3 |
Крутящий момент, приложенный к шарниру между двумя секциями передней левой ноги |
-1 |
1 |
|
4 |
Крутящий момент, приложенный к шарниру между туловищем и передним правым бедром |
-1 |
1 |
|
5 |
Крутящий момент, приложенный к шарниру между двумя секциями передней правой ноги |
-1 |
1 |
|
6 |
Крутящий момент, приложенный к шарниру между туловищем и задним левым бедром |
-1 |
1 |
|
7 |
Крутящий момент, приложенный к шарниру между двумя секциями задней левой ноги |
-1 |
1 |
Пространство наблюдений для робота описывается значениями положения различных частей его тела и скоростями этих отдельных частей. Следовательно, для описания состояния робота используется вектор размерности 27, который описан в таблице 2.
Таблица 2. Пространство состояний агента (робота Ant)
|
Индекс |
Наблюдение |
Значение |
|
0 |
Координата туловища по оси z |
Позиция (м) |
|
1 |
x – ориентация туловища |
Угол наклона (рад) |
|
2 |
y – ориентация туловища |
Угол наклона (рад) |
|
3 |
z – ориентация туловища |
Угол наклона (рад) |
|
4 |
w – ориентация туловища |
Угол наклона (рад) |
|
5,7, 9, 11 |
Углы между туловищем и секциями каждой ноги |
Угол наклона (рад) |
|
6, 8, 10, 12 |
Углы между двумя секциями каждой ноги |
Угол наклона (рад) |
|
13 |
Скорость движения туловища по x - координате |
Скорость (м/c) |
|
14 |
Скорость движения туловища по y - координате |
Скорость (м/c) |
|
15 |
Скорость движения туловища по z - координате |
Скорость (м/c) |
|
16 |
x – координата угловой скорости движения туловища |
Угловая скорость (рад/c) |
|
17 |
y – координата угловой скорости движения туловища |
Угловая скорость (рад/c) |
|
18 |
z – координата угловой скорости движения туловища |
Угловая скорость (рад/c) |
|
19, 21, 23, 25 |
Угловая скорость угла между туловищем и секциями каждой ноги |
Угол наклона (рад) |
|
20, 22, 24, 26 |
Угловая скорость угла между двумя секциями каждой ноги |
Угол наклона (рад) |
Вознаграждение для агента состоит из трёх частей:
-
1)награда за устойчивость (если агент оставался на ногах до конца эпизода);
-
2)награда за движение вперёд, которая измеряется как скорость продвижения робота вперёд;
-
3)отрицательная награда за величину действия (нормировка по действиям).
Симуляция, или как её называют иначе – эпизод, заканчивается при достижении агентом (роботом) заданной точки, при перевороте робота или при окончании длины симуляции (1000 временных интервалов).
Описание алгоритма решения задачи
Рис. 1. Схема взаимодействия агента и среды
Для решения задачи использовался алгоритм, основывающийся на Policy Gradient подходе. Такой класс алгоритмов использует оценки градиента функционала по параметрам стратегии (политики). Алгоритм Proximal Policy Optimization (PPO) [Proximal Policy Optimization] считается устоявшимся решением в обучении с подкреплением, именно этот алгоритм использовался при создании алгоритма, победившего профессионалов в киберспортивной игре Dota 2.
Алгоритм Proximal Policy Optimization
Гиперпараметры:
M – количество параллельных сред,
N – длина роллаутов (траекторий),
B – размер мини-батчей (пакетов данных),
N_epoch – количество эпох (итераций) обучения,
Оптимизатор – Stohastic Gradient Descent (используется для оптимизации нейронных сетей критика и актёра).
Псевдокод алгоритма:
На каждом шаге:
-
1)В каждой параллельной среде собрать роллаут длины N, используя стратегию , сохраняя вероятности выбора действий как , а выход критика на встреченных состояниях как .
-
2)Для каждой пары s, a из роллаутов посчитать одношаговую оценку Advantage:
где done – показатель конца эпизода.
Посчитать Advantage оценку:
-
3)Для t от (N - 2) до 0:
-
4)Посчитать целевое значение (таргет) для критика:
-
5)Составить датасет из шестёрок:
Для каждого мини-батча:
-
Вычислить ошибку критика:
-
Сделать шаг градиентного спуска по , используя .
-
Нормализовать по батчу, чтобы в среднем значения равнялись 0, а дисперсия – 1.
-
Посчитать коэффициенты для выборки по важности (importance sampling):
-
Посчитать обрезанную версию градиента:
-
Вычислить градиент для нейронной сети актёра:
-
Сделать шаг градиентного подъёма по , используя .
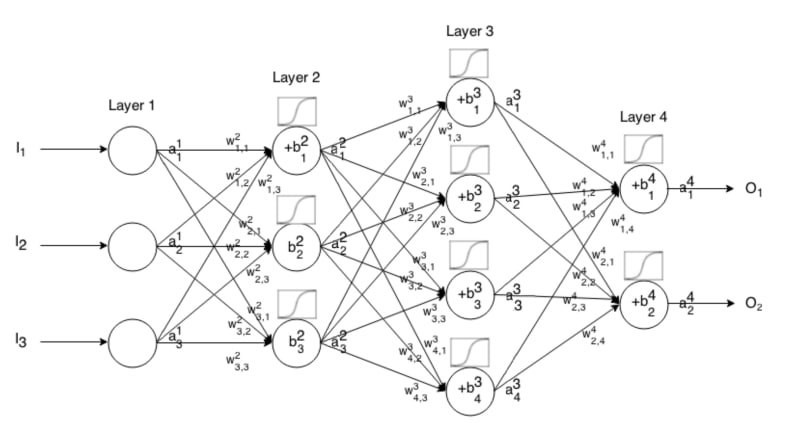
Работы, рассматривающие решение поставленной задачи, как правило, использовали данный алгоритм, в котором в роли аппроксиматора политики агента выступала полносвязная глубокая нейронная сеть. Архитектура такой сети представляет собой перцептрон, состоящий из двух скрытых линейных слоёв с гиперболическим тангенсом (tanh) в качестве функции активации и количеством нейронов 64, 64 и 8 для актёра и 64, 64 и 8 для критика соответственно. Пример архитектуры такой сети представлен на рисунке 2.
Рис. 2. Схема архитектуры полносвязной нейронной сети
Выходная размерность сети соответствует пространству действий агента, следовательно, при увеличении размерности задачи возникали проблемы с увеличением количества выходных нейронов сети актёра.
В данной работе для борьбы с «проклятием размерности» используется подход, который подразумевает замену представления пространства действий и, соответственно, замену архитектуры сети. Ключевой идеей является использование сети, состоящей из энкодера и декодера. Благодаря такому подходу, становится возможным использование последовательностей входных данных и сохранение внутренней информации самой последовательности без потери качества.
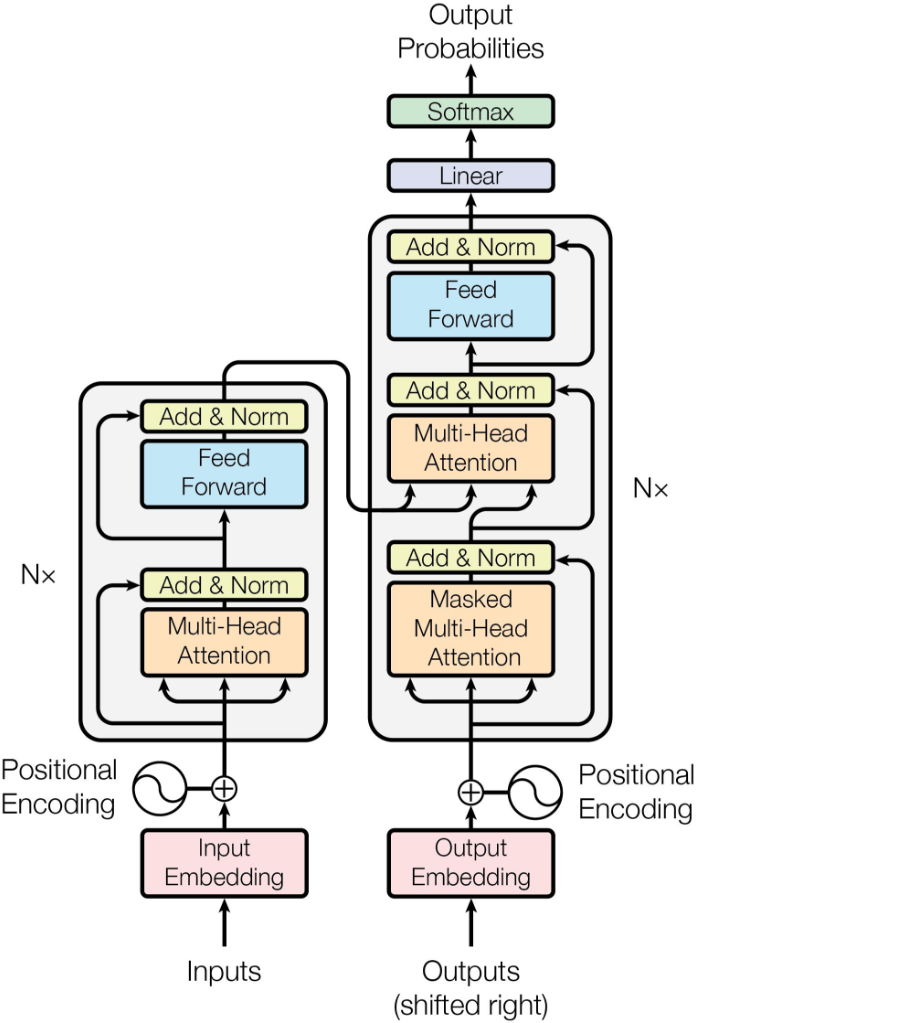
Основой для разработки сети в текущей работе послужила статья [Attention Is All] об архитектуре сети Transformer, которая полностью основывается на механизме внимания и не использует рекуррентные слои или слои свертки. Ниже, на рисунке 3, представлено устройство сети Transformer.
Рис. 3. Схема архитектуры Tranformer
Основная идея заключается в том, что сеть разбивается на два блока – энкодер и декодер, слева и справа на рисунке 3 соответственно.
Энкодер последовательно применяет к исходной последовательности N блоков, в каждом из которых входные данные проходят через два основных слоя: multi-head attention и feed-forward. Multi-head attention состоит из нескольких наборов self-attention, которые можно по-другому назвать слоями самовнимания, они отличаются от обычного слоя внимания тем, что выходом слоя являются новые представления всё той же последовательности, каждый элемент которой напрямую взаимодействует друг с другом. Сама реализация данного слоя изложена в [Attention Is All], стоит отметить лишь то, что благодаря распараллеливанию слоёв внимания удается уловить намного больше внутренних зависимостей последовательности, что и реализует слой multi-head attention.
В декодере используется похожая структура, но основное отличие заключается в слое cross-attention (кросс-внимание). В данном слое для формирования результата многоголового внимания используются результаты обработки энкодером входной последовательности. Кроме того, на вход энкодеру подается вся последовательность сразу, в то время как декодер обрабатывает последовательность итерационно, т.е. на каждом шаге он получает информацию о текущем элементе последовательности (токене) и обо всех предыдущих, не заглядывая вперёд.
Элементы, описывающие торс робота:
Элементы, описывающие переднюю левую ногу робота:
Элементы, описывающие переднюю правую ногу робота:
Элементы, описывающие заднюю левую ногу робота:
Элементы, описывающие заднюю правую ногу робота:
После представления вектора состояния в виде последовательности формируются входные эмбеддинги (векторные представления данных) и передаются в энкодер сети Transformer. В отличие от [Attention Is All] позиционное кодирование не используется, поскольку информация о позициях ног и туловища в последовательности входного вектора не оказывает влияния на дальнейшее обучение, критична лишь их исходная инициализация.
Для использования декодера необходимо определить размерность выходного вектора. Так как агент способен управлять лишь шарнирными соединениями своих ног, то выходной вектор последовательности сокращается до 4 элементов, соответствующих каждой ноге робота. При этом каждый элемент содержит 2 величины крутящего момента для шарниров ноги. Благодаря такому подходу удалось сократить пространство действий до размерности 2, что в четыре раза меньше исходной размерности вектора действий из таблицы 1.
Результаты экспериментов
Обучение агента проводилось на GPU, чтобы ускорить распараллеленные процессы в нейронной сети. Было запущено два эксперимента с одинаковым набором гиперпараметров для алгоритма PPO (см. табл.3), реализованном в библиотеке StableBaselines на языке Python [Stable Baselines Documentation].
Таблица 3. Гиперпараметры алгоритма обучения с подкреплением PPO
|
Learning rate |
0,0003 |
|
Количество шагов в эпизоде |
1000 |
|
Размер мини-батча |
64 |
|
Коэффициент дисконтирования
|
0,99 |
|
Коэффициент для оценки GAE
|
0,95 |
|
Размер clip PPO |
0,2 |
|
Максимальное значение для обрезки градиента |
0,5 |
|
Размер окна для усреднения оценки политики агента |
100 |
В первом эксперименте использовалась полносвязная нейронная сеть с параметрами, описанными в таблице 4.
Таблица 4. Параметры полносвязной нейронной сети для алгоритма PPO
|
Количество скрытых слоёв |
2 |
|
Количество нейронов в скрытых слоях |
64 |
|
Функция активации |
Tanh |
Во втором эксперименте использовалась сеть архитектуры Transformer, параметры которой описаны в таблице 5.
Таблица 5. Параметры нейронной сети архитектуры Transformer для алгоритма PPO
|
Количество голов multi-head attention энкодера |
4 |
|
Функция активации в полносвязном слое энкодера |
ReLu |
|
Количество голов в masked multi-head attention декодера |
4 |
|
Функция активации в полносвязном слое декодера |
Relu |
|
Количество нейронов в слоях энкодера |
64 |
|
Количество нейронов в слоях декодера |
64 |
|
Размерность слоя эмбеддинга для энкодера |
32 |
|
Размерность слоя эмбеддинга для декодера |
32 |
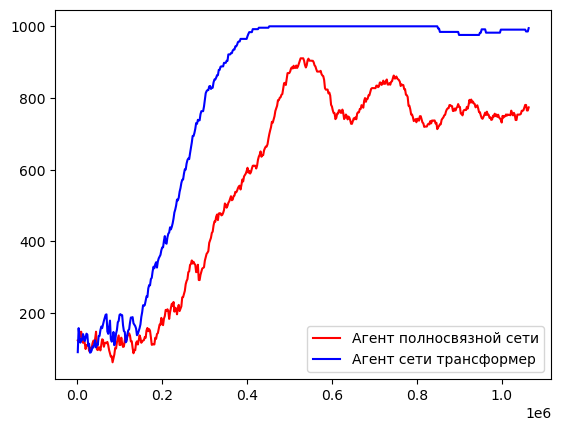
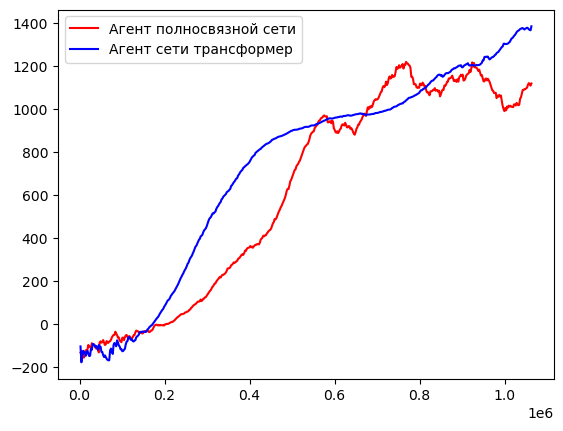
После обучения агента на более чем 1 миллионе шагов в среде были получены следующие результаты. Для агента, обученного с помощью полносвязной сети длина эпизода достигала максимум 910 шагов в среде и среднее значение награды за эпизод 1212, синяя кривая на рисунках 3 и 4. Награда формируется из суммы нескольких значений:
-
1)награда за пребывание в «здоровом» состоянии, если муравей не перевернулся = 1;
-
2)награда за продвижение вперёд = 0.05;
-
3)штраф за слишком большое (по модулю) действие = 0 .
Рис. 4. График зависимости средней длины эпизода агентов от количества шагов обучения.
Результаты для агента, который был обучен с помощью сети Transformer, были выше, чем у предыдущего агента. Длина эпизода для него сошлась к значению 1000 уже за 475000 шагов в среде, в то время как роботу, политика которого основывалась на полносвязной сети, не удалось достигнуть такого результата за всё время обучения. Также, награда у нового агента достигала отметки в 1380 единиц и продолжала расти. Графики для данного агента описываются красной кривой на рисунках 4 и 5.
Рис. 5. График зависимости средней награды агентов от количества шагов обучения.
Заключение
Апробация новой архитектуры сети Transformer для аппроксимации стратегии обучения агента позволила добиться положительных результатов. Благодаря использованию архитектуры сети Transformer при обучении робота передвижению, удалось сузить пространство действий, увеличить продолжительность эпизода и получить награду, превосходящую результат, получаемый для решения аналогичной задачи с использованием глубокой полносвязной нейронной сети. Исходя из всего вышесказанного, можно сделать вывод, что применение архитектуры нейронной сети Transformer для использования в решении задач обучения с подкреплением может привести к улучшению качества результатов обучения и снижению вычислительных нагрузок.