Количественная оценка степени сформированности навыков командной деятельности

В статье представлена методология количественной оценки сформированности навыков командной деятельности с использованием схемы треугольника и математических моделей на основе матриц вероятностей переходов. Исследование фокусируется на анализе индивидуальной и совместной согласованной деятельности участников в экспериментальных условиях, заключающихся в работе на тренажере по совместному управлению воздушным судном. В анализе результатов применяются цепи Маркова, что позволяет детализировать динамику выполнения задач, выявляя ключевые аспекты взаимодействия участников. Результаты подтверждают эффективность предложенного подхода для анализа и улучшения координации действий в команде.

Введение

Изучение процесса формирования и объективной количественной оценки навыков командной деятельности приобретает все большее значение в современных исследованиях. Особенно актуально это для подготовки операторов сложных технических систем, включая экипажи воздушных судов.

Традиционные подходы к оценке навыков командной работы, несмотря на сохраняющуюся актуальность, часто оказываются недостаточными для объективной количественной оценки, требующейся в условиях высокоавтоматизированных и динамических систем. В этом контексте становится необходимым разработка методологий, которые могут интегрировать формальные методы анализа и современные математические модели для более точного и всестороннего анализа командного взаимодействия.

Одним из перспективных подходов в этой области является использование «схемы треугольника», предложенной в работе [1], которая позволяет оценивать навыки командной деятельности на основе анализа взаимодействия участников как в индивидуальном, так и в командном контексте. Применяемый аппарат анализа опирается на сравнения матриц вероятностей переходов между типами элементарных операций, что позволяет анализировать динамику деятельности.

Методология оценки навыков командной деятельности

При оценке навыков командной деятельности по «схеме треугольника» [1] пара испытуемых реализует вместе и индивидуально согласованную деятельность, например, совместное пилотирование воздушного судна. Работа направлена на достижение конкретной цели, понятной испытуемым. В процессе деятельности применяется специализированный программно-аппаратный комплекс для регистрации протоколов деятельности и формирования матриц вероятностей переходов между типами операций [9].

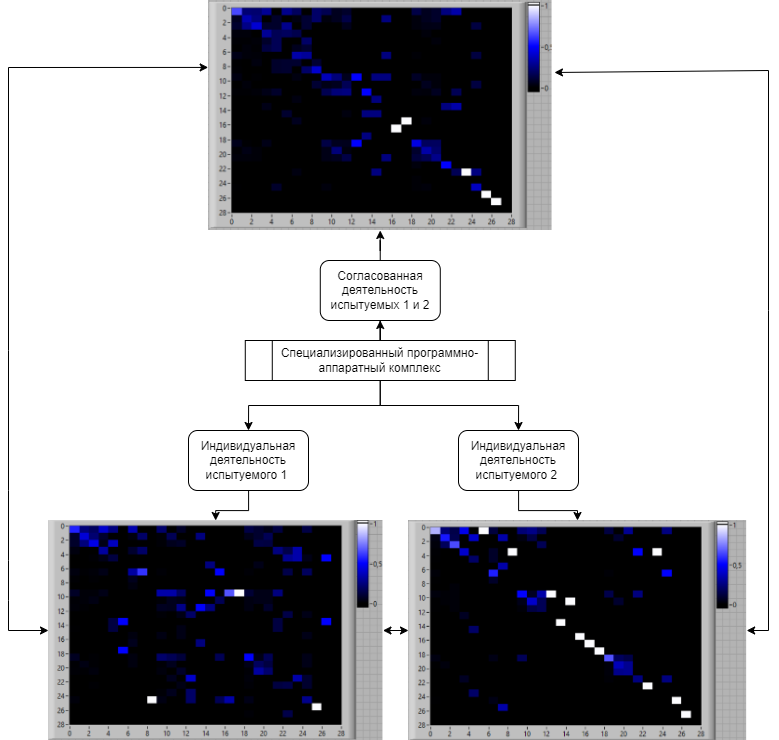
Валидность оценки степени сформированности навыков командной работы определяется структурой сравнений по «схеме треугольника» (рисунок 1).

Согласно этой схеме, согласованная деятельность испытуемых сопоставляется с их индивидуальной деятельностью, которая служит эталоном согласованных командных действий. Использование матриц вероятностей переходов между типами элементарных операций в сочетании с построением сопутствующих квантовых представлений и их сравнениями в спектральной метрике [8; 11-14] позволяет проводить количественные сопоставления различных вариантов действий испытуемых и учитывать особенности конкретной выполняемой работы.

Применение «схемы треугольника» включает три основных этапа:

1. индивидуальная деятельность первого участника;

2. индивидуальная деятельность второго участника;

3. согласованная деятельность обоих участников.

Анализ полученных результатов позволяет выявить особенности индивидуальной деятельности и оценить степень согласованности в совместной работе.

Математическая модель согласованной деятельности испытуемых

Следуя работам [2; 13; 14], согласованная деятельность испытуемых формализуется посредством матриц вероятностей переходов между выполняемыми ими элементарными операциями. Рассматриваемая модель, названная математической моделью сопутствующей деятельности, представляет вероятностную динамику выполнения рассматриваемых типов элементарных операций как марковский процесс с дискретными состояниями и дискретным временем (цепь Маркова):

Эффективность решения прикладных задач регулируется степенью детализации учитываемых элементарных операций, представляющих и конкретизирующих адаптацию модели к предметной области [10].

Данные о деятельности участников представляются в виде матриц вероятностей переходов (рисунок 2) между типами выполняемых элементарных операций. Сравнение этих матриц позволяет выявить особенности индивидуальной и совместной деятельности, оценить уровень согласованности действий и определить ключевые аспекты взаимодействия [6].

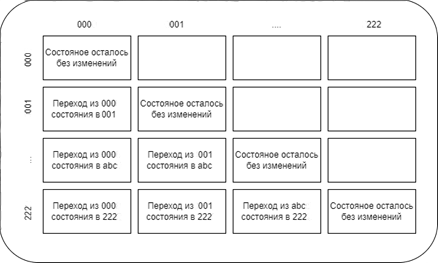
Матрица вероятностей переходов представляет собой квадратную матрицу, где каждая строка и каждый столбец соответствуют различным типам допустимых элементарных операций, выполняемых участниками. Элементами матрицы являются вероятности переходов от одного типа операций к другому в последующий момент времени [7].

Рис. 2. Структура матрицы вероятностей переходов между 33 типами выполняемых элементарных операций

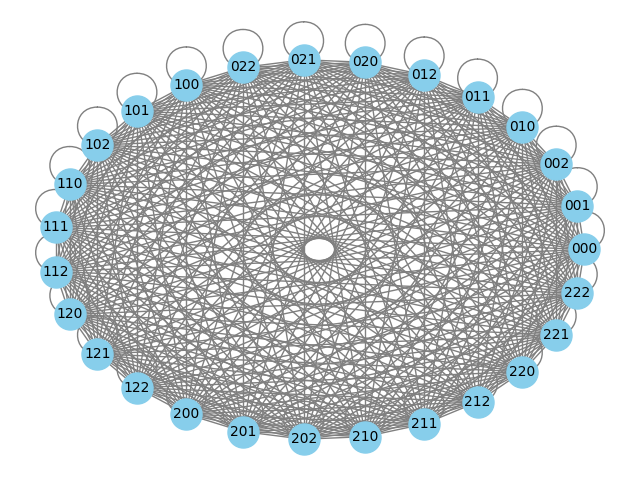
Каждой из таких матриц может быть поставлен в соответствие полносвязный граф, позволяющий анализировать взаимодействия между типами элементарных операций (рисунок 3).

Рис. 3. Полносвязный граф

Такой граф наглядно демонстрирует все возможные переходы и связи, что полезно для моделирования и оптимизации сложных процессов.

Анализ экспериментальных данных

Для исследования возможностей рассматриваемого подхода были проведены эксперименты в двух различных образовательных учреждениях: в каждом учреждении проводилось три эксперимента на паре лиц с расстройствами аутистического спектра, результаты которых показаны в таблицах 1 и 2. Следуя работам [11-12], полученные количественные оценки выражаются через Λ-статистики Уилкса.

Таблица 1 . Значения обратной статистики Уилкса (1- ) в первом эксперименте

Таблица 2. Значения обратной статистики Уилкса (1-Λ) экспериментов во втором эксперименте

В первом эксперименте участвовали ученики 9-го класса, все участники были мужского пола. Во втором эксперименте в исследовании приняли участие студенты 3-го и 4-го курсов, также мужского пола.

Тестирование проводилось на летном тренажере, представляющем собой программно-аппаратный комплекс, имитирующий для работающих на нем испытуемых полет воздушного судна [1; 3-5]. Он управляется экипажем с разделением между пилотами каналов управления, которые в реальном полете контролирует один человек. Экипаж в составе двух находящихся рядом пилотов должен обеспечить корректное управление воздушным судном путем согласованных действий, получая в реальном времени в удобной, понятной и доступной форме информацию о результатах своей деятельности, включая отображение положения воздушного судна относительно земной поверхности [10-11].

Эксперимент прошел в штатном режиме. Однако во время первого полета у некоторых участников возникли сложности в управлении, что является типичным для начальных этапов освоения нового материала. Несмотря на это, к третьему эксперименту все участники успешно разобрались с задачами и продемонстрировали заметное улучшение в управлении и координации действий, как в индивидуальной, так и в командной работе.

После нормализации данных с целью сравнительной оценки результатов первого и второго участника и их совместной деятельности были получены следующие результаты (см. таблицы 3, 4).

Таблица 3. Результаты первого эксперимента

Таблица 4. Результаты второго эксперимента

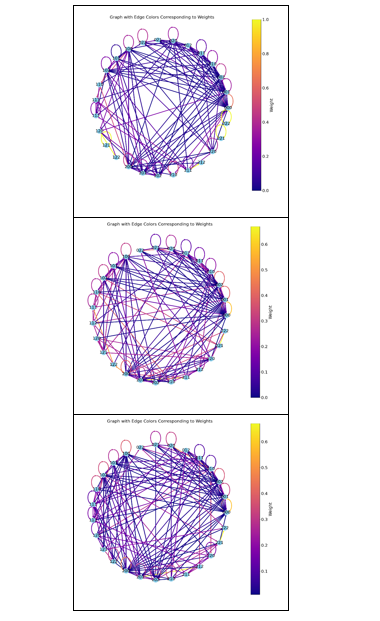
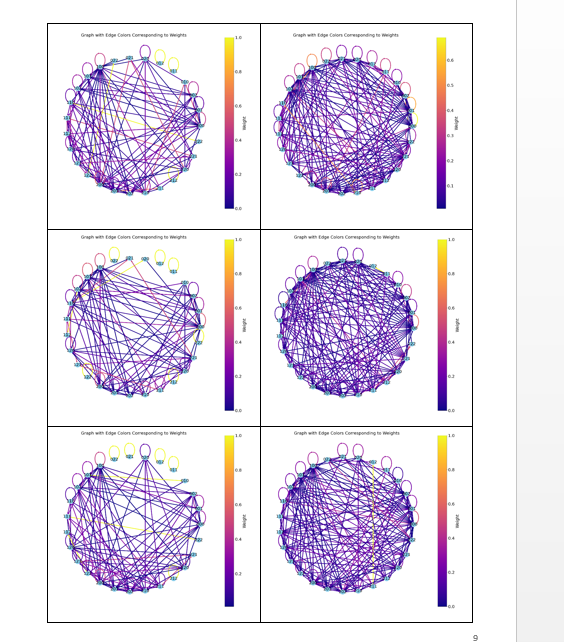
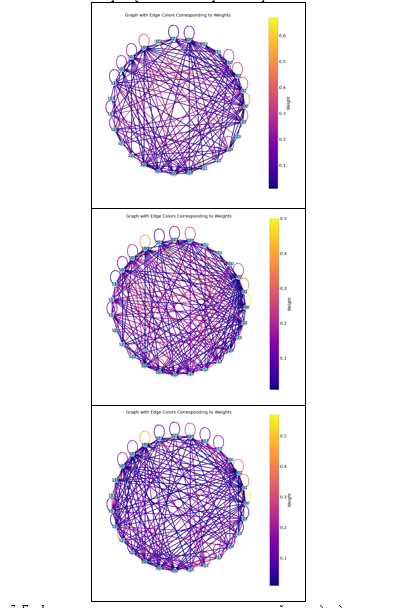
Для анализа данных были построены графы, представляющие матрицы вероятностей переходов между типами операций. Визуализация этих графов позволяет наглядно представить и сравнить действия участников, выявить ключевые особенности их индивидуальной и совместной деятельности (рисунки 4-7).

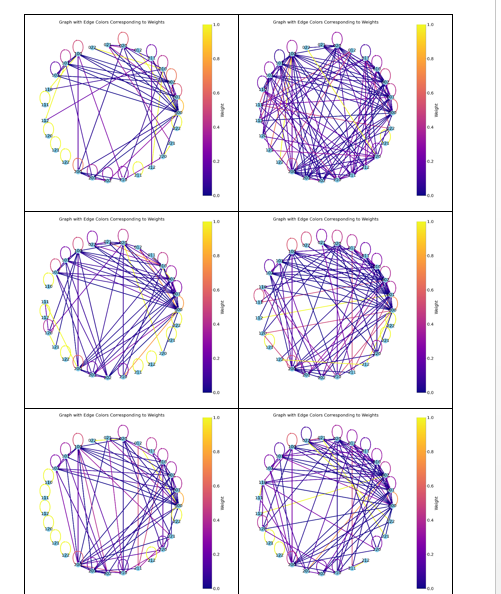
Рис. 4. Графы, построенные на основе матриц вероятностного перехода первого и второго участников первого эксперимента

Рис. 5. Графы, построенные на основе матриц вероятностей переходов для представления совместной деятельности первого эксперимента

Рис. 6. Графы, построенные на основе матриц вероятностей переходов для первого и второго участников второго эксперимента

Рис. 7. Графы, построенные на основе матриц вероятностей переходов для совместной деятельности в рамках второго эксперимента

Анализ результатов первого эксперимента демонстрирует, что второй участник показал прогресс на 82,2% в навыках индивидуальной деятельности, что свидетельствует о значительном улучшении его навыков и повышении эффективности работы. Значения статистики Уилкса показывают, что первый пилот превосходит второго по качеству пилотирования, что подтверждает его более высокий уровень навыков.

Совместная деятельность также продемонстрировала улучшение: показатели снизились с 1,07 в первом эксперименте до 0,9 в третьем, что говорит о повышении координации и эффективности в командной работе. Это позволяет предположить, что существует положительная корреляция между прогрессом второго пилота и улучшением их совместной деятельности, что подчеркивает важность индивидуального роста для успешной командной работы.

Результаты второго эксперимента, демонстрируют, что первый участник показал стабильные показатели.

Второй участник продемонстрировал значительное улучшение: его результаты снизились с 8,83 в первом эксперименте до 5,78 в третьем, что указывает на успешную адаптацию к задачам и повышение эффективности выполнения работы.

Совместная деятельность в основном соответствует показателям второго пилота и изменяется по мере его развития. В начале первый пилот положительно влияет на взаимодействие, однако к третьему эксперименту, вероятно из-за усталости первого пилота, происходит перераспределение ролей, и второй пилот начинает доминировать, что отражается на результатах.

Основные результаты и выводы

Проведённое исследование подтвердило высокую эффективность представленного подхода к анализу взаимодействий как на индивидуальном, так и на командном уровнях. Использование схемы оценки, основанной на сравнении индивидуальных и согласованных действий, позволило выявить важные аспекты взаимодействия и уровня координации между участниками экспериментов.

Экспериментальные данные подтвердили, что «схема треугольника» не только помогает выявить особенности индивидуального выполнения заданий, но и позволяет оценивать степень согласованности в командной деятельности. Применение матриц вероятностей переходов между типами элементарных операций, обеспечило подробный количественный анализ взаимодействий, способствуя более глубокому пониманию динамики изменений в навыках участников и их влияния на общую эффективность команды.

Результаты экспериментов показали значительное улучшение координации действий и качества выполнения задач по мере накопления опыта и адаптации участников. Эффективность совместной деятельности увеличивалась по мере развития индивидуальных навыков, что подчеркивает значимость как индивидуального, так и командного обучения для достижения оптимальных результатов. Особое внимание следует уделить динамическому распределению ролей и взаимной поддержке внутри команды, что также отражается на изменениях показателей совместной деятельности.

Таким образом, «схема треугольника», применяемая в данном исследовании, доказала свою ценность как инструмент для глубокого анализа и объективной количественной оценки навыков командной работы. Обнаруженные улучшения и значимые аспекты взаимодействия подчеркивают необходимость продолжения исследований в этом направлении с целью дальнейшего совершенствования методик оценки и развития навыков командной деятельности в сложных технических системах.

1. Куравский Л.С., Юрьев Г.А., Михайловский М.А., Несимова А.О., Юрьева Н.Е., Поляков Б.Ю. Формирование навыков командной деятельности и их объективная количественная оценка на основе квантовых представлений // Экспериментальная психология. 2024. Том 17. № 2. С. 154–177. DOI: 10.17759/exppsy.2024170210
2. Куравский Л.С., Козырев А.Д., Грешников И.И.Математическая модель сопутствующей деятельности пилотов и ее применение для объективной оценки его состояния и профессиональной подготовки // Экспериментальная психология. Том 17. № 1. С. 161—180. DOI:10.17759/exppsy.2024170111
3. Ермаков С.С., Савенков. Е.А., Катышев Д.А. Влияние современных симуляционных тренажеров на развитие навыков командной работы: согласованных действий и коммуникации // Экспериментальная психология. 2024. Том 13. № 2. С. 131–141.
4. Ермаков С.С., Быстрова Ю.А. Анализ исследований роли компьютерных тренажеров в формировании, измерении и совершенствовании навыков командной работы // Экспериментальная психология. 2024. Том 17. № 2. С. 113–127.
5. Грешников И.И., Куравский Л.С., Юрьев Г.А. Принципы построения программно-аппаратного комплекса для интеллектуальной поддержки экипажа и оценки уровня его подготовки // Моделирование и анализ данных. 2021. Том 11. № 2. C. 5-30.  DOI: 17759/mda.2021110201
6. Kabi, M. Dhar, P. Arora, B.B. Bhardwaj, N. Chowdhury, S. Rao Effectiveness of a Simulation-Based Training Program in Improving the Preparedness of Health Care Workers Involved in the Airway Management of COVID-19 Patients // Cureus. 2021. Vol. 13(8). Article ID e17323. 8 p.  DOI: 10.7759/CUREUS.17323
7. Rasch G. Probabilistic models for some intelligence and attainment tests. (Copenhagen, Danish Institute for Educational Research), expanded edition with foreword and afterword by B.D. Wright. Chicago: The University of Chicago Press, 1980.
8. Nielsen Michael A. & Chuang Isaac L. Quantum Computation and Quantum Information. Cambridge University Press, 2010. 702
9. Kuravsky L.S., Yuryev G.A., Zlatomrezhev V.I.New approaches for assessing the activities of operators of complex technical systems // Experimental psychology (Russia). Vol. 12. № 4. 27—49. DOI:10.17759/exppsy.2019120403
10. Kuravsky L.S., Yuryev G.A.A novel approach for recognizing abnormal activities of operators of complex technical systems: three non-standard metrics for comparing performance patterns [Электронный ресурс] // International Journal of Advanced Research in Engineering and Technology (IJARET). Vol. 11(4). P. 119—136. URL: http://www.iaeme.com/IJARET/issues.asp?JType=IJARET&VType=11&IType=4 (дата обращения: 06.07.2024).]
11. Kuravsky L.S., Greshnikov I.I., Yuryev G.A., Zlatomrezhev V.I.Synthesis of Civil Aircraft Control Using Empirical Data and Quantum Filtering // Lobachevskii J. Math. 2023. 44(6). P. 2079—2100.
12. Kuravsky L.S., Greshnikov I.I., Kozyrev A.D., Kosachevsky S.G., Frolova L.I., Zakharcheva A.A. A mathematical model for representing the related operator professional activities and its relevant diagnostic assessment based on the quantum representations // Lobachevskii J. Math. 2024. 45(6), pp. 2549—2566. DOI: 10.1134/S1995080224602819
13. Kuravsky L.S. Simplification of Solving Diagnostics Problems by Convolution of Applied Markovian Models into the Quantum Representations // Lobachevskii J. Math. 2022. 43(7). P.1669—1682.
14. Kuravsky L.S.Modeling Dynamical Behavior of Stochastic Systems: Spectral Analysis of Qubit Representations vs the Mutual Markovian Model Likelihood Estimations // Lobachevskii J. Math. 2021. 42(10). P. 2364—2376.