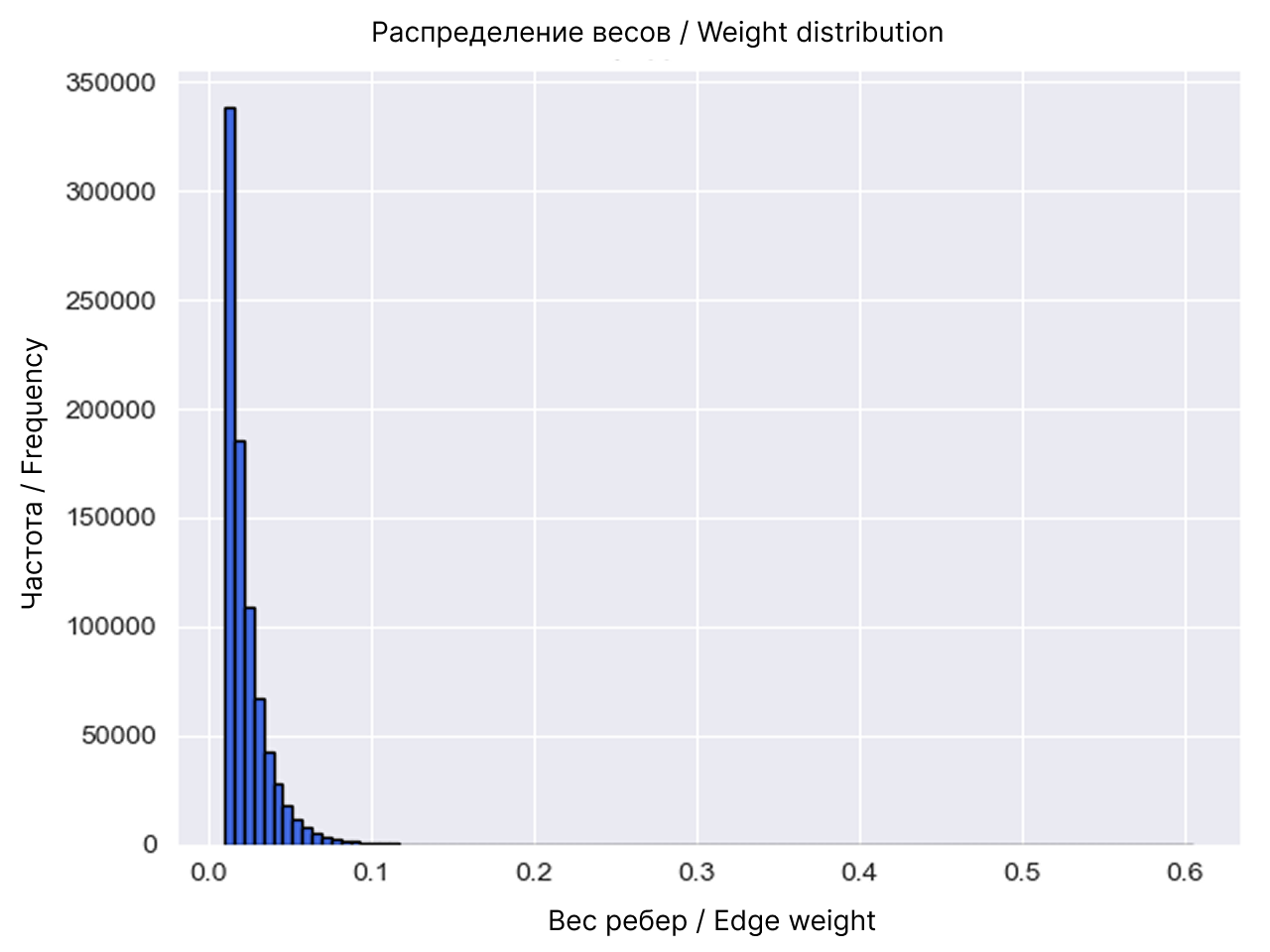
Введение
В различных ситуациях, требующих принятия решений, выбор, осуществляемый индивидами, часто основывается на информации, поступающей от их окружения [Jackson]. Таким окружением может быть семья, сверстники, коллеги по работе, средства массовой информации и другие источники. Так, исследование [Гегель] показало, что 40% старшеклассников ориентируются на мнение семьи при выборе профессии, 22% – на школу, а 13% – на сверстников.
Влияние окружения распространяется и на другие сферы, например принятие решений о покупках. Отзывы друзей, рекомендации в соцсетях и лидеры мнений могут существенно повлиять на поведение потребителей [Berger; Chevalier; Iyengar]. Это особенно важно в маркетинге, где информация о брендах и акциях формирует потребительские предпочтения. Понимание этих механизмов необходимо для разработки эффективных стратегий продвижения.
Интересный пример влияния социальной группы на индивидуальное поведение был представлен в эксперименте, описанном в работе [Milgram], в ходе которого исследователи попросили группы испытуемых различного размера (от одного до пятнадцати человек) встать на улице и смотреть в небо. Эксперимент показал, что влияние группы на поведение усиливается с увеличением её размера: один человек, смотрящий в небо, почти не привлекал внимания, несколько человек – немного больше, а группа из 15 человек заставляла 45% прохожих остановиться и смотреть вверх.
Исследование [Padgett] показало, что центральное положение в социальной сети, как у семьи Медичи в эпоху Возрождения, способствует успеху в политике. Их доминирование стало возможным благодаря сети брачных и деловых связей, что подчеркивает важность социальных связей для достижения влияния и успеха.
Необходимость определения влиятельных (важных) узлов в сетях возникает в различных задачах: ранжирования поисковых запросов (например, алгоритм PageRank [Полякова], который был предложен Google в конце 1990-х годов, что вместе с развитием сети Интернет положило начало активному изучению мер центральности [Центральность в социальных] как эффективному инструменту для анализа структуры сетей), работы рекомендательных систем [Дьяконов], анализа распространения инфекций, слухов или мнений [Утакаева], а также оценки устойчивости информационных сетей [Волков].
В социальных сетях определение ключевых акторов имеет особое значение для понимания поведения системы и формирования эффективных стратегий взаимодействия. От этого зависит способность предсказать последствия различных действий, таких, как распространение информации, влияние на общественное мнение или реакции на маркетинговые кампании.
Целью данной работы является сравнительный анализ различных мер центральности для задачи обнаружения влиятельных агентов в сети региональных маркет-сообществ. Для достижения этой цели проводится обзор популярных метрик, таких как степень центральности, посредничество, близость, собственный вектор, PageRank и центральность по Кацу. Ожидается, что результаты анализа помогут выбрать наиболее эффективную меру центральности для выявления ключевых агентов, влияющих на распространение информации в маркет-сообществах.
Основная часть
Меры центральности
В литературе по сетевому анализу для оценки значимости узлов используются четыре базовые характеристики, каждая из которых отражает тот или иной аспект положения узла в сети [Jackson]:
− степень узла;
− близость узла;
− промежуточность узла;
− важность соседей узла.
Степень узла отражает, насколько связан узел с соседями, близость – насколько просто некоторому узлу добраться до других в сети, промежуточность – насколько связующим является узел в сети, а важность соседей узла – насколько важны (влиятельны) его соседи.
В анализе социальных сетей очень часто для обнаружения наиболее влиятельных акторов используются индексы (меры) центральности. Существуют более 400 различных индексов центральности [Центральность в социальных]. Некоторые из них требуют учета локальных характеристик узла для количественной оценки его важности, к таким мерам относится, например, центральность степени. Другие индексы используют глобальную информацию обо всей сети – это центральность близости, посредничества, собственного вектора, центральность по Кацу, PageRank и другие.
Центральность степени
Изначально степенная центральность возникла в теории графов. Степенью вершины в графе G называется количество ребер, инцидентных вершине v. Данная мера центральности является базовой и для ненаправленных невзвешенных сетей определяется как:
|
|
|
(1) |
|
|
|
(2) |
|
|
|
(3) |
Параметр в данном определении позволяет придать большую значимость степени узла, а придает большее значение силе. Выбор точного значения параметра зависит от конкретных требований и его определение может быть затруднено. Метод выбора оптимального значения параметра был предложен в статье [Wei].
Центральность близости
Центральность близости (closeness centrality) показывает, насколько удален данный узел сети от остальных. Данный индекс центральности является величиной, обратной среднему расстоянию от некоторого узла в сети до всех остальных. Для заданного узла v она определяется как [Freeman]:
|
|
|
(4) |
где d – функция расстояния в графе (количество ребер на кратчайшем пути) между узлами u и v, n – количество узлов в сети, а множитель n-1 нормирует размер графа. Суммирование осуществляется по всем узлам сети u за исключением v. Поскольку путь между любыми двумя вершинами u и v существует только для связных графов, то и данное определение центральности применимо только к ним. Существует также расширение этого типа центральности на взвешенные сети. В них центральность узла v определяется как:
|
|
|
(5) |
Центральность промежуточности
В основе центральности промежуточности (betweenness centrality) лежит предположение о том, что информация всегда проходит по кратчайшим путям между вершинами, а ее расчет основан на количестве таких кратчайших путей, на которых расположена вершина. Центральность промежуточности определяется как [Freeman]:
|
|
|
(6) |
|
|
|
(7) |
где число в знаменателе – это максимальное количество путей в графе порядка n, проходящих через узел v.
Центральности на основе собственного вектора (спектральные)
Центральность на основе собственного вектора является обобщением степенной центральности. При этом, если центральность степени назначает одинаковую важность соседям узла, что для измерения важности узлов в социальных сетях может оказаться недостаточным, то центральность собственного вектора назначает соседям узла различную значимость. Вследствие этого, узел, связанный с очень важными узлами, сам становится важным:
|
|
|
(8) |
|
|
|
(9) |
|
|
|
(11) |
|
|
|
(12) |
|
|
|
(13) |
Еще одним примером данного типа центральностей является центральность PageRank. Данный тип центральности основан на модели случайного блуждания и определяется как:
|
|
|
(14) |
PageRank используется в библиометрии, анализе социальных и информационных сетей, дорожных сетей и во многих других приложениях.
Материалы и методы
Таблица 1 / Table 1
Категории ключевых слов
Keyword categories
|
Ключевые слова / Keywords |
Количество сообществ / Number of communities |
|
1. Магазин, товары, продажа, купить, каталог, аксессуар, прайс, опт, розница, скидки, распродажа, интернет-магазин, заказ, доставка, услуги, мастер-класс, обучение, курсы, консультация, аренда, ремонт, красота, салон / 1. Shop, goods, sale, buy, catalog, accessory, price list, wholesale, retail, discounts, sale, online store, order, delivery, services, master class, training, courses, consultation, rent, repair, beauty, salon |
3409 |
|
2. Одежда, обувь, аксессуары, стиль, мода, бренд, джинсы, футболки, шубы, пальто, сумки, рюкзаки, украшения, ювелирные изделия, часы, ремни, шарфы, перчатки, одежда больших размеров, секонд-хенд, винтаж / 2. Clothing, shoes, accessories, style, fashion, brand, jeans, T-shirts, fur coats, coats, bags, backpacks, jewelry, jewelry, watches, belts, scarves, gloves, plus-size clothing, second-hand, vintage |
1529 |
|
3. Электроника, телефоны, смартфоны, планшеты, компьютеры, ноутбуки, бытовая техника, гаджеты, оргтехника, аксессуары для техники, наушники, телевизоры, видеокамеры, игровые консоли, игровые устройства, ремонт техники, Apple, Android / 3. Electronics, phones, smartphones, tablets, computers, laptops, household appliances, gadgets, office equipment, accessories for appliances, headphones, televisions, video cameras, game consoles, gaming devices, repair of appliances, Apple, Android |
839 |
|
4. Мебель, декор, интерьер, посуда, текстиль, ковры, обои, шторы, лампы, осветительные приборы, кухонные принадлежности, бытовая химия, садовая техника, сад, огород, инструменты / 4. Furniture, decor, interior, tableware, textiles, carpets, wallpaper, curtains, lamps, lighting, kitchen utensils, household chemicals, gardening equipment, garden, vegetable garden, tools |
684 |
|
5. Косметика, парикмахерская, уход, макияж, парфюмерия, уход за кожей, маникюр, педикюр, волосы, витамины, спорт, фитнес, массаж, SPA, йога, плавание, бассейн, здоровый образ жизни, медицинские услуги, диета, натуральные продукты, татуировки, пирсинг / 5. Cosmetics, hairdressing, grooming, makeup, perfumes, skin care, manicure, pedicure, hair, vitamins, sports, fitness, massage, SPA, yoga, swimming, pool, healthy lifestyle, medical services, diet, natural products, tattoos, piercing |
1624 |
|
6. Игрушки, коляски, детская одежда, товары для малышей, детская мебель, конструкторы, настольные игры, рюкзаки для школы, книги для детей, обучение для детей, кружки, секции, репетиторы / 6. Toys, strollers, children's clothing, baby products, children's furniture, construction kits, board games, backpacks for school, books for children, education for children, clubs, sections, tutors |
1387 |
|
7. Еда, продукты, напитки, доставка еды, фермерские продукты, экотовары, выпечка, кондитерские изделия, торты на заказ, пироги, рестораны, сеть ресторанов, кафе, сеть кафе, столовая, чай, кофе, конфеты, доставка обедов, здоровое питание, пекарня, хлеб, рыба / 7. Food, groceries, drinks, food delivery, farm products, eco-products, pastries, confectionery, cakes to order, pies, restaurants, restaurant chain, cafe, cafe chain, canteen, tea, coffee, sweets, lunch delivery, healthy food, bakery, bread, fish |
1138 |
|
8. Рукоделие, handmade, DIY, вязание, вышивка, шитьё, рисование, творчество, арт, декупаж, скрапбукинг, фотография, видеосъёмка, музыка, танцы, мастер-класс, вокал / 8. Needlework, handmade, DIY, knitting, embroidery, sewing, drawing, creativity, art, decoupage, scrapbooking, photography, videography, music, dancing, master class, vocals |
1322 |
|
9. Спорт, спортивное питание, снаряжение, бег, тренажёры, фитнес, плавание, бассейн, велоспорт, велосипед, туризм, кемпинг, альпинизм, охота, рыбалка, спортивное снаряжение, лыжи, сноуборд, активный отдых, теннис, яхта, яхтклуб, скалолазание, ролики, волейбол, каток, коньки, скейтборд, хоккей, футбол, баскетбол, турник, брусья, гимнастика, бокс, бодибилдинг, пауэрлифтинг, настольный теннис, большой теннис, физические упражнения, горнолыжный / 9. Sports, sports nutrition, equipment, running, fitness equipment, fitness, swimming, pool, cycling, cycling, hiking, camping, mountaineering, hunting, fishing, sports equipment, skiing, snowboarding, outdoor activities, tennis, yacht, yacht club, rock climbing, roller skates, volleyball, ice rink, ice skating, skateboard, hockey, football, basketball, horizontal bar, uneven bars, gymnastics, boxing, bodybuilding, powerlifting, table tennis, lawn tennis, physical exercises, skiing |
1006 |
|
10. Авто, автомобили, автозапчасти, мотоциклы, велосипеды, аксессуары для авто, аренда авто, грузоперевозки, ремонт авто, тюнинг, электросамокаты, скутеры, запчасти / 10. Auto, cars, auto parts, motorcycles, bicycles, car accessories, car rental, cargo transportation, car repair, tuning, electric scooters, scooters, spare parts |
585 |
|
11. Подарки, сувениры, цветы, праздничные услуги, организация мероприятий, воздушные шары, украшения, кейтеринг, фотограф, видеооператор, ведущий, тамада, фейерверк, салют, декор для праздников / 11. Gifts, souvenirs, flowers, holiday services, event management, balloons, decorations, catering, photographer, videographer, presenter, toastmaster, fireworks, fireworks, holiday decor |
1009 |
|
12. Обучение, курсы, репетиторство, мастер-классы, вебинары, онлайн-школы, языковые курсы, повышение квалификации, подготовка к экзаменам, карьерное консультирование, тренинги, программирование / 12. Training, courses, tutoring, workshops, webinars, online schools, language courses, advanced training, exam preparation, career counseling, trainings, programming |
770 |
|
13. Зоотовары, корм для животных, аквариумы, аквариумные рыбки, аксессуары для животных, одежда для собак, уход за животными, ветеринарные услуги, дрессировка, гостиницы для животных, кошки, собаки, питомцы / 13. Pet supplies, pet food, aquariums, aquarium fish, animal accessories, dog clothes, animal care, veterinary services, training, animal hotels, cats, dogs, pets |
287 |
|
14. Кино, театры, концерты, билеты, квесты, экскурсии, парки, клубы, игровые центры, настольные игры, настолки, видеоигры, туризм, путешествия, квизы / 14. Movies, theaters, concerts, tickets, quests, excursions, parks, clubs, game centers, board games, board games, video games, tourism, travel, quizzes |
628 |
Для обнаружения сообществ нами использовался лувенский метод. Меры центральности рассчитывались с использованием библиотеки NetworkX и языка программирования Python (версия 3.8). Визуализация сети и распределения мер центральности проводились с помощью matplotlib, seaborn и средств визуализации с открытым исходным кодом Gephi.
Результаты
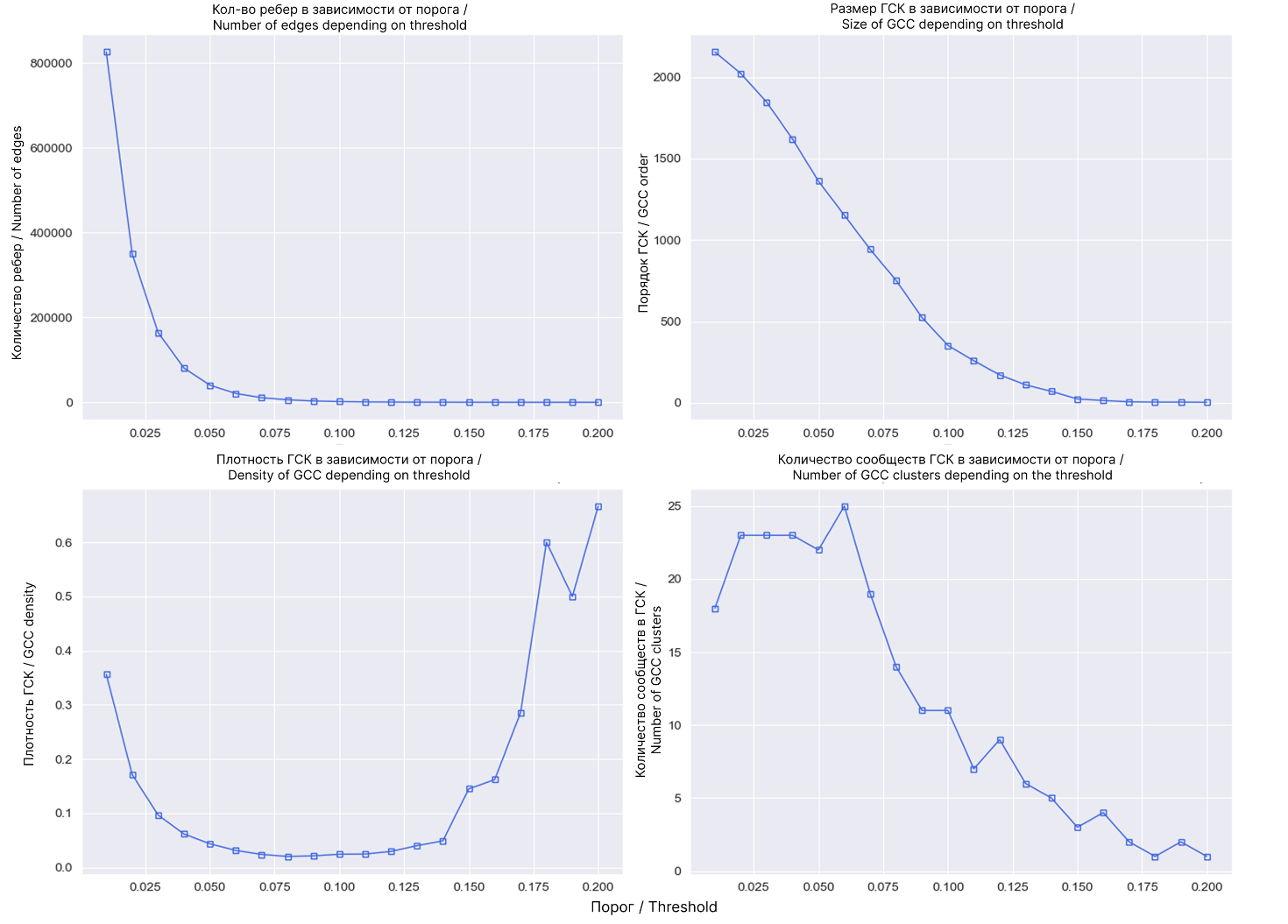
Рис. 2. Влияние порога на структуру сети
Fig. 2. The effect of the threshold on the network structure
Таблица 2 / Table 2
Характеристики сети маркет-сообществ
Characteristics of a network of market communities
|
Характеристики сети / Network Characteristics |
Значения / Values |
|
Модулярность / Modularity |
0.53 |
|
Количество узлов / Number of nodes |
942 |
|
Количество ребер / Number of edges |
10648 |
|
Средняя степень / The average degree |
22.607 |
|
Средняя взвешенная степень / Weighted average degree |
1.957 |
|
Плотность / Density |
0.024 |
|
Количество треугольников / Number of triangles |
95398 |
|
Коэффициент кластеризации / Clusterization coefficient |
0.436 |
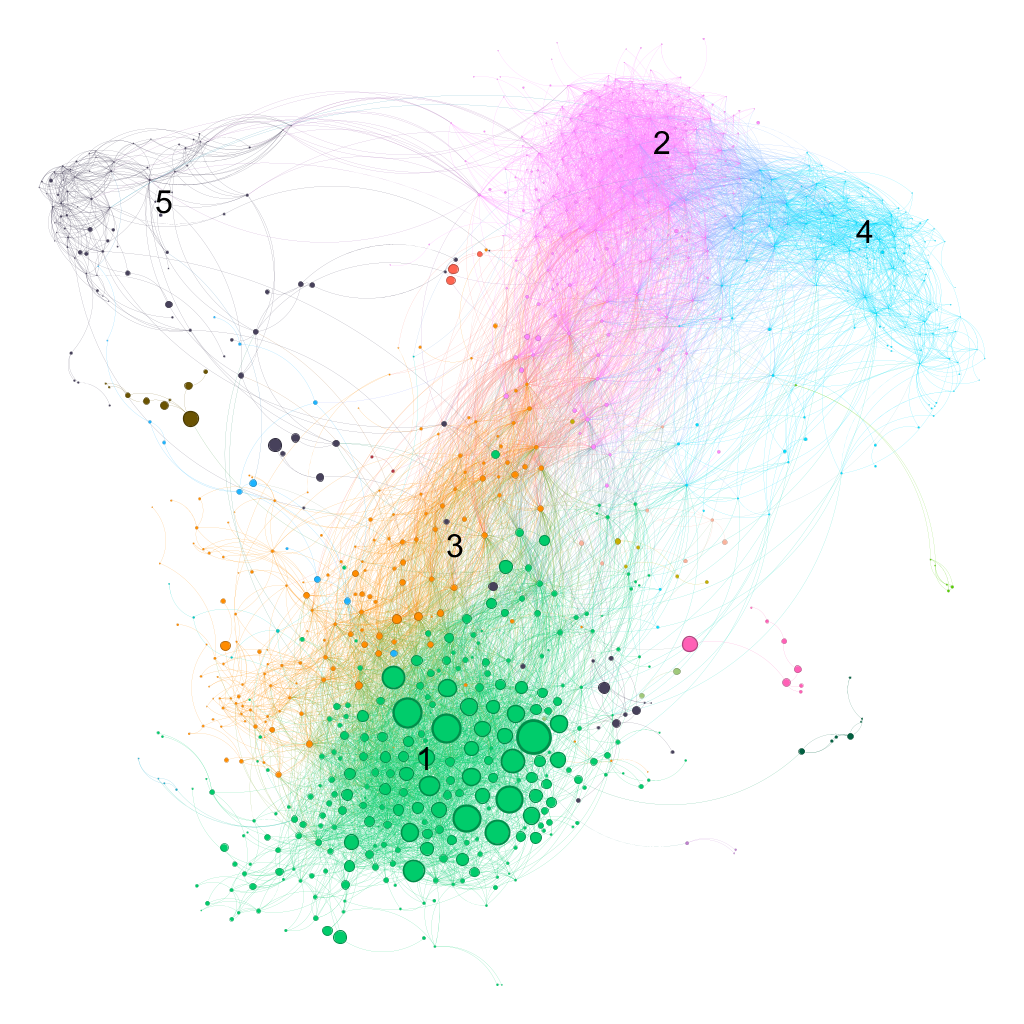
В таблице 3 отражены доли узлов в кластерах.
Таблица 3 / Table 3
Доли узлов в кластерах
Shares of nodes in clusters
|
Номер кластера / Cluster Number |
1 |
2 |
3 |
4 |
5 |
|
Доля узлов, % / The proportion of nodes, % |
27.39 |
22.51 |
16.45 |
14.12 |
11.46 |
Модулярность исследуемой сети составляет 0.53, что свидетельствует о наличии выраженной кластерной структуры. В сети 942 узла и 10648 рёбер. Средняя степень узлов равна 22.607, следовательно, каждое из маркет-сообществ имеет пересекающуюся аудиторию с более чем 22 другими. Средняя взвешенная степень составляет 1.957. Плотность сети, равная 0.024, говорит о её разреженности, поскольку из всех возможных связей реализована лишь малая их часть. Сеть характеризуется высокой степенью кластеризации: коэффициент кластеризации равен 0.436, количество треугольников в сети достигает 95398, что указывает на тенденцию к триадическому замыканию, типичному для социальных сетей с сильными внутренними связями. Средняя длина пути составляет 3.722, что свидетельствует о высокой связности сети, несмотря на ее разреженность.
На рис. 4 представлены распределения значений центральности степени, собственного вектора, центральности по Кацу, промежуточности, близости и PageRank.
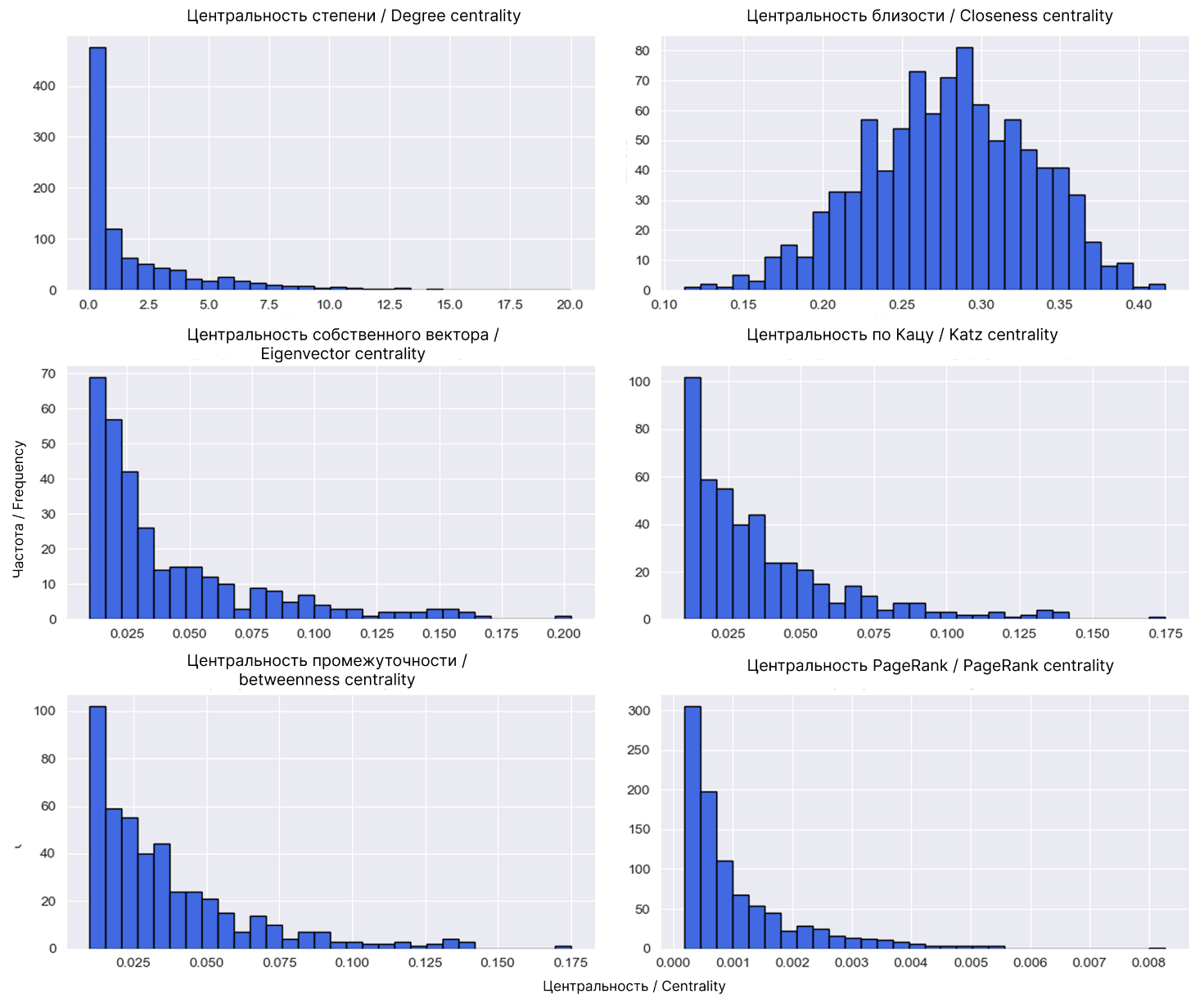
Рис. 4. Распределения индексов центральности
Fig. 4. Distributions of centrality indices
В качестве примера наиболее центральных сообществ в таблице 4 представлены результаты по пяти сообществам наиболее центральными по Кацу и PageRank.
Таблица 4 / Table 4
Показатели мер центральностей
Indicators of centrality measures
|
№ |
Название группы / Group name |
Количество подписчиков / Number of subscribers |
Показатель / Indicator |
|
Центральность по Кацу / Katz centrality |
|||
|
1 |
Ремонт ванных комнат в Архангельске «Уют Центр» |
1471 |
0.174894 |
|
2 |
Фотограф Евгения Кожина Архангельск-Северодвинск |
1376 |
0.141196 |
|
3 |
Superburg - бургеры, роллы, хот-доги, чиабатта |
1495 |
0.138296 |
|
4 |
Натуральная косметика Savonry в Архангельске |
857 |
0.136912 |
|
5 |
ТОРТ✿*♡MARy CAKe♡*✿ на заказ АРХАНГЕЛЬСК |
4426 |
0.134763 |
|
PageRank |
|||
|
1 |
Ремонт ванных комнат в Архангельске «Уют Центр» |
1471 |
0.008269 |
|
2 |
Кафе - кондитерская «Венский пекарь» |
12556 |
0.005481 |
|
3 |
ТОРТ✿*♡MARy CAKe♡*✿ на заказ АРХАНГЕЛЬСК |
4426 |
0.005430 |
|
4 |
Фотограф Евгения Кожина Архангельск-Северодвинск |
1376 |
0.005309 |
|
5 |
Натуральная косметика Savonry в Архангельске |
857 |
0.005221 |
По данным таблицы 4 прослеживается корреляция между различными индексами центральности. Корреляционная матрица (таблица 5) отражает взаимосвязь между индексами, используемыми при выявлении ключевых агентов.
Таблица 5 / Table 5
Корреляционная матрица индексов центральности
Correlation matrix of centrality indices
|
Центральность / Centrality |
|
|
|
|
|
|
|
|
1 |
0.72086 |
0.61648 |
0.843130 |
0.95324 |
0.93246 |
|
|
0.72086 |
1 |
0.47175 |
0.62388 |
0.61611 |
0.70260 |
|
|
0.61648 |
0.47175 |
1 |
0.42489 |
0.69391 |
0.50089 |
|
|
0.84313 |
0.62388 |
0.42489 |
1 |
0.71343 |
0.97634 |
|
|
0.95324 |
0.61611 |
0.69391 |
0.71343 |
1 |
0.81805 |
|
|
0.93246 |
0.70260 |
0.50089 |
0.97634 |
0.81805 |
1 |
Высокая корреляция между центральностью собственного вектора, центральностью по Кацу и PageRank указывает на высокую глобальную значимость обнаруженных маркет-сообществ в структуре сети. Эти узлы, вероятно, имеют устойчивые связи с другими важными участниками и играют ключевую роль в формировании ядра сети. Низкие значения корреляции центральности промежуточности с другими мерами (0.42−0.69) отражают её уникальность: узлы, обнаруженные данной мерой, влияют на процессы распространения информации в сети.
На основе распределений центральности проведена оценка устойчивости сети при удалении наиболее центральных узлов по сравнению со случайным удалением (рис. 5). Поскольку исходная сеть совпадает с размером ГСК, то в начальный момент ее размер совпадает со всей сетью и равен 1.0.
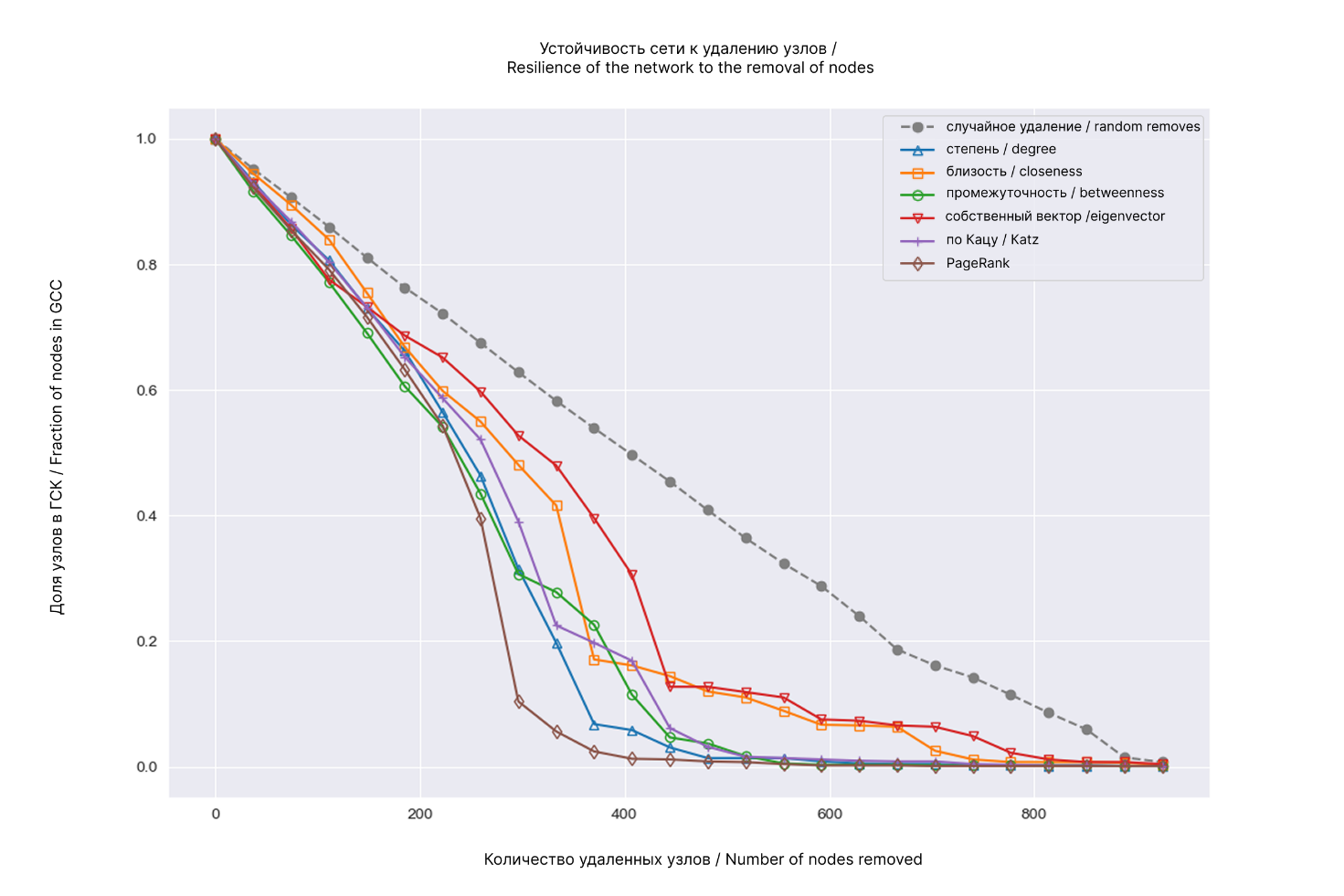
Рис. 5. Результат теста устойчивости сети маркет-сообществ
Fig. 5. The result of the stability test of the network of market communities
При рандомизированном выборе узлов для удаления – относительный размер гигантской связной компоненты линейно зависит от числа удаленных узлов. Напротив, при выборе наиболее центральных узлов сеть распадается (таблица 6).
Таблица 6 / Table 6
Устойчивость сети
Network stability
|
При удалении / When deleting |
Network stability |
|||||
|
|
|
|
|
|
|
|
|
20% узлов / 20% of nodes |
0.65393 |
0.66454 |
0.59660 |
0.68471 |
0.62314 |
0.64756 |
|
40% узлов / 40% of nodes |
0.06794 |
0.16561 |
0.22399 |
0.38854 |
0.02447 |
0.19745 |
Сеть оказалась наиболее уязвимой при выборе центральных по PageRank узлов для удаления. Количество узлов в исходной сети составляло 952, а при удалении примерно 40% узлов в соответствии с центральностью степени и PageRank сеть стала почти фрагментированной. Удаление узлов в соответствии с центральностью собственного вектора меньше всего влияет на структуру сети (0.68 для 20% и 0.39 для 40%) по сравнению с остальными.
Устойчивость сети маркет-сообществ тесно связана с выбором стратегии удаления узлов. Наиболее критичными для её структуры являются более важные по PageRank узлы. Эти узлы, вероятно, играют ключевую роль в распространении информации через сеть, а их удаление значительно снижает её функциональность.
Обсуждение результатов
Ключевыми маркетинговыми сообществами, вовлеченными в распространение информации в сети, с точки зрения ее структуры оказались относительно небольшие (по количеству подписчиков) сообщества. Наиболее центральные сообщества преимущественно имеют праздничную тематику. Анализ устойчивости показал относительно высокую надежность сети (полная фрагментация достигается при удалении свыше 40% узлов), а при удалении 20% наиболее центральных узлов сохраняется от 0.59 (в случае центральности промежуточности) до 0.68 (в случае центральности собственного вектора).
Заключение
В статье проведен обзор базовых мер центральности, включающих центральность степени, близости, посредничества, собственного вектора, центральности по Кацу, PageRank. Построена сеть маркет-сообществ города Архангельска на основе данных онлайн-платформы социальных сетей ВКонтакте. Определены допустимые значения коэффициента Жаккара.
Анализ распределений центральности показал, что, как и в большинстве социальных сетей, в сети маркет-сообществ преобладают низкостепенные узлы и лишь небольшой процент узлов выступает в роли хабов. На основе распределений центральности, проведена оценка устойчивости сети маркет-сообществ. Показано, что данная сеть оказалась наименее устойчивой при использовании центральности PageRank, а наиболее устойчивой – при использовании центральности собственного вектора.
Полученные результаты подтверждают ключевую роль хабов в социальных сетях. Оценка устойчивости сети при использовании той или иной меры центральности может быть использована для измерения степени влияния в социальных сетях. В дальнейшем исследовании предполагается использование выявленных ключевых игроков для моделирования стратегического взаимодействия в задаче дележа сети как неоднородного ресурса.
Ограничения. В исследовании рассматриваются сообщества, предоставляющие данные о подписчиках, однако, существуют сообщества, в которых подписчики скрыты - такие сообщества не учтены в сети, что может несколько исказить реальную структуру сети. При фильтрации ребер использовалась простейшая эвристика на основе связности гигантской связной компоненты, в дальнейшем можно использовать более сложные методы (например, фильтр диспаритета).
Limitations. The research considers communities that provide data on subscribers, however, there are communities in which subscribers are hidden - such communities are not taken into account in the network, which can somewhat distort the real structure of the network. When filtering edges, the simplest heuristics based on the connectivity of a giant connected component were used, in the future, more complex methods can be used (for example, a disparity filter).