Изучение теории алгоритмов включается в образовательные программы вузов по специальностям 09.02.03 «Программирование в компьютерных системах», 09.03.01 «Программная инженерия и компьютерные науки», 02.03.03 «Математическое обеспечение и администрирование информационных систем». Её цель – формирование знаний об основных результатах теории алгоритмов; развитие логической и алгоритмической интуиции как в математике, так и в информатике; формирование и развитие у студентов понимания уровня строгости математической модели. Здесь ключевая математическая модель – машина Тьюринга (МТ). В учебниках и учебных пособиях теме о конечных автоматах и МТ уделяется значительное внимание (Поляков, Скорубский, 2012), (Лукин, Чернышов, 2021), (Чернецкая, 2022).
Практика показывает, что студенты нередко испытывают трудности в изучении дисциплин, связанных с теорией автоматов. Причина кроется в том, что для этого требуется высокий уровень абстракции, в то время как автомат обычно ассоциируется с чем-то материальным. Поэтому у преподавателя стоит задача подать материал максимально наглядно без потери строгости. Здесь большую пользу может принести программное средство для демонстрации как статического представления автомата, так и его работу, что способствуют лучшему усвоению материала.
Базовые знания и теория в полном объеме даются в известных монографиях (Ахо, Ульман,1978) и (Хопкрофт, Мотвани, Ульман, 2002).
Рассмотрим представление машины Тьюринга. Она задаётся перечислением символов алфавита, множеством состояний и набором правил перехода, по которым она работает. Диаграмму состояний можно определить в виде графа, на дугах которого отмечаются действия машины: перемещение головки по ленте и запись символа на ленту. Подобные диаграммы строятся и для других моделей вычислений.
Существует множество различных инструментов для построения диаграмм состояний, графов и машин Тьюринга (Редактор графов, 2025), (Эмулятор машины Тьюринга, 2025), (Finite Automata Designer, 2025), (Инструмент для построения диаграммы состояния, 2025) и др. Однако не все они удобны для демонстрации: как правило, нет возможности анимации действий не только машин Тьюринга, но и существенно более простых моделей: автоматов с магазинной памятью (МП-автоматов) и конечных автоматов (КА). Кроме того, они обычно предназначены для решения ограниченного набора задач для конкретных моделей и имеют сложный интерфейс.
Наиболее известный и популярный инструмент для визуализации объектов теории формальных языков – программа JFLAP, разрабатываемая в университете Дьюка с 1990 года (JFLAB, 2018). Она имеет развитый функционал, позволяет моделировать автоматы разных типов, она мультиплатформенная (написана на языке Java). Но для её установки требуется регистрация (проприетарная лицензия). Кроме того, она достаточно объемная: более 300 папок и 6000 файлов, что затрудняет ее изучение и модификацию.
Для проведения практических занятий на построение автоматов и грамматик есть онлайн-сервис (AutomataTutor, 2025), распространяемый под лицензией Apache 2.0. Он позволяет преподавателям составлять упражнения, а студентам отправлять выполненные задания, который автоматически проверяются.
В курсе теории алгоритмов тема машин Тьюринга основная, но лишь одна из многих. Общим для всех видов автоматов является граф состояний. Существует множество различных программ для построения графов и решения задач с их помощью. Наиболее подходящей для использования оказалась программа с открытым кодом, разработанная И. Уоллесом (Wallace Evan, 2010). Программа имеет простой интерфейс и позволяет строить размеченные графы, в которых можно выделить конечные состояния. Построенные графы статичны и сохраняются в локальной памяти с помощью средства localstorage.
Однако для учебных целей необходима не только возможность визуализации автоматов. Нужна и анимация их работы, и пригодность для решения задач. Важно показать как формальное определение автоматов, так и динамику работы в виде последовательности конфигураций. Для машин Тьюринга есть программа (Эмулятор машины Тьюринга, 2025), разработанная именно для обучения, но в ней нет диаграмм. Диаграммы МТ строятся в системе (The busy beaver challenge, 2025), но для этого необходимо написать программу определения автомата на некотором псевдокоде.
Для использования в учебном процессе желательно иметь удобный инструмент, допускающий расширения для разных моделей и разных задач. Основой должен служить построитель графов, на элементы которого налагаются ограничения, соответствующие выбранной модели. Этот инструмент должен предоставлять преподавателю среду для подготовки демонстрационных примеров (презентаций) к лекциям, разработки заданий для контрольных и лабораторных работ. Кроме того, нужно, чтобы студенты, в свою очередь, могли использовать его при изучении соответствующих тем, решать задачи и готовить отчеты к ним.
Одним из авторов (Чернышовым Л.Н.) построено как раз такое программное средство: построитель конечных автоматов FSMD (см. www.chernyshov.com/FSM). Его основная цель – графическое представление конечных автоматов. В свою очередь, графическая форма может быть легко преобразована в текстовую. Это позволяет встраивать изображение в документы разных форматов: SVG – в HTML-документы, LaTeX – в офисные документы, JSON – в JavaScript-программы. Кроме того, предусмотрено преобразование графов в специальные представления, которые удобно использовать в программах на разных языках (в частности, в Haskell).
Основные возможности программы следующие:
- построение диаграмм конечных автоматов, автоматов с магазинной памятью, машин Тьюринга;
- экспорт диаграмм в JSON, SVG, LaTeX;
- импорт диаграмм (как отдельной диаграммы, так и набора) в JSON-формате;
- генерация по диаграммам формальных определений КА, МР-автомата, МТ, регулярных грамматик с проверкой корректности диаграмм;
- задание команд МТ в сокращенном виде (можно не указывать запись текущего символа и движение головки);
- задание МТ и автоматическая генерация диаграмм по компактному стандартному описанию;
- возможность определения детерминированности автоматов;
- нахождение пустых и недостижимых состояний в автоматах;
- сохранение рабочей диаграммы и комментария к ней в локальной памяти;
- формирование наборов диаграмм и хранение их в локальном хранилище;
- демонстрация пошаговой работы автоматов с визуализацией рабочей ленты (магазинной памяти для МП-автомата) и конфигураций как в ручном режиме, так и в автоматическом с заданием интервала времени;
- демонстрация вывода цепочек в регулярной грамматике;
- генерация случайных диаграмм;
- хранение на сервере демонстрационных наборов автоматов;
- доступ к базе данных МТ определенного вида для их исследования.
Для использования в учебном процессе созданы демонстрационные наборы автоматов. Они служат вспомогательным материалом при чтении лекций и на практических занятиях. Примеры, на которых они построены, взяты из монографий (Ахо, Ульман,1978), (Хопкрофт, Мотвани, Ульман, 2002) и учебных пособий (Поляков, Скорубский, 2012), (Лукин, Чернышов, 2021). Там они снабжены комментариями и подробно разбираются.
Важная особенность интерфейса программы состоит в том, что на экране одновременно показаны формальное определение автомата, диаграмма состояний и последовательность конфигураций (рис.1). Зачастую студенты с трудом могут дать формальное математическое определение автомата и результата его работы. Отображение различных форм одной и той же абстракции поможет понять суть и запомнить определения.
Программный код FSMD, как и ядро построителя диаграмм, открытый. Это даёт возможность ставить задачи по расширению возможностей и развивать силами студентов.
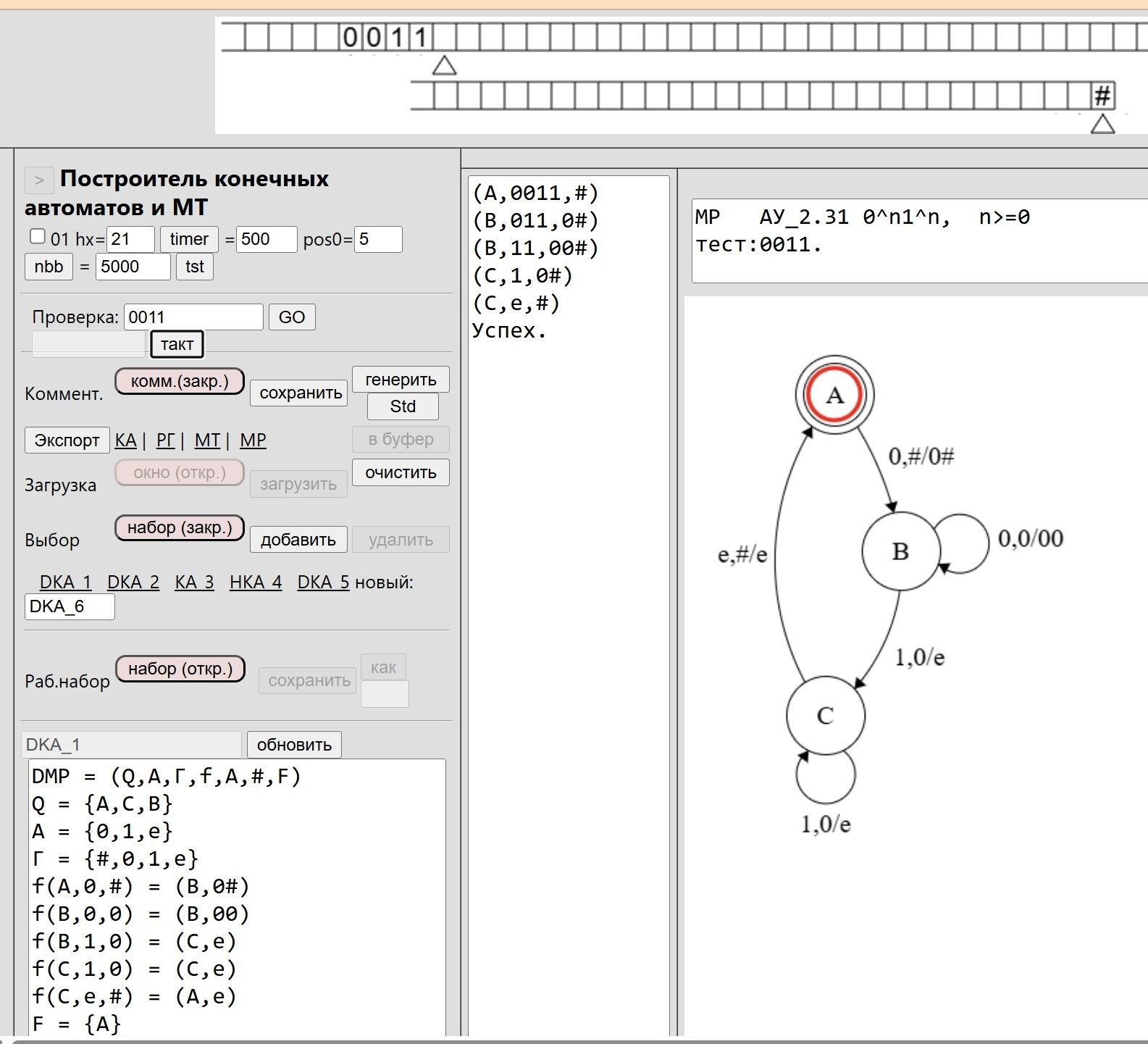
Рис.1. Моделирование работы МП-автомата
Fig. 1. Simulation of pushdown automaton
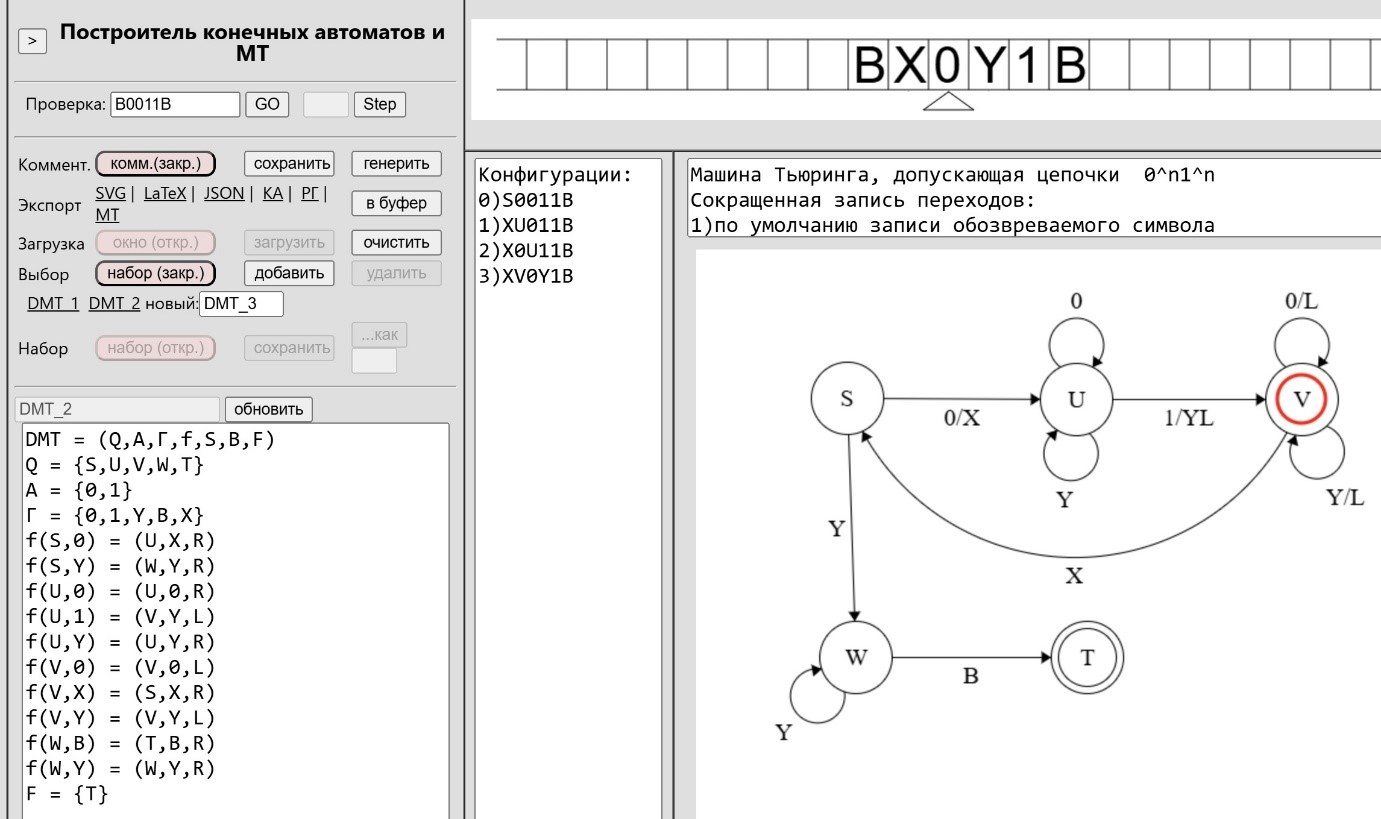
Рис. 2. Моделирование работы машины Тьюринга
Fig. 2. Simulation of Turing machine operation
В программе предусмотрены параметры для настройки отображаемой ленты: ее размеры, число клеток на экране, ограничение с одного из концов и начальное состояние. Часть примеров МТ соответствует правилам, принятым в (Хопкрофт, Мотвани, Ульман, 2002), а именно: пустые клетки заполнены символом «B», который включается в алфавит МТ. При этом отмечается только клетки, которые расположены непосредственно слева и справа от обрабатываемой цепочки. В другом режиме лента полностью заполняется нулями, и МТ может начинать работу, когда на ленте нет символов, отличных от нуля.
В случае двухсимвольного алфавита {0,1} МТ можно задать не только диаграммой, но и описанием в виде строки. Строка составляется их последовательности подстрок, разделенных знаком «_». Первая подстрока определяется командами перехода из начального состояния A в зависимости от 0 и 1 в текущей позиции на ленте. Например, если f(A,0) = (B, 1, R) и f(A,1) = (C, 0, L), то строкой будет «1RB0LC». Далее следуют подстроки, полученные для состояний B. C и т. д. Последнее состояние считается конечным. Если перехода по какому-либо символу нет, соответствующая подстрока заменяется на «---». Диаграмма по такой строке, которая задается в комментариях, строится автоматически.
Для МТ с начальной нулевой лентой естественным образом возникает задача, известная как проблема «усердного бобра» (The busy beaver challenge, 2025). Она состоит в том, чтобы среди всех МТ с n-состояниями и алфавитом {0,1} (их конечное число) найти машину BB(n), которая делает максимальное число шагов S(n) до остановки и записывает на ленту максимальное число единиц (n).
Алан Тьюринг в 1936 году доказал, что не существует алгоритма, который для любой МТ мог бы определить, остановится ли она. Поэтому задача нахождения значений функций S(n) и (n) для n>4 оказывается непростой. Для n=5 задача была решена только в 2024 году. В программе FSMD приводится набор решений для n от 1 до 5, а для n=6 и n=7 построены наилучшие решения, обнаруженные в июне и мае 2025 года соответственно. На рисунке 3 приводятся диаграммы МТ для n=5 и n=6.
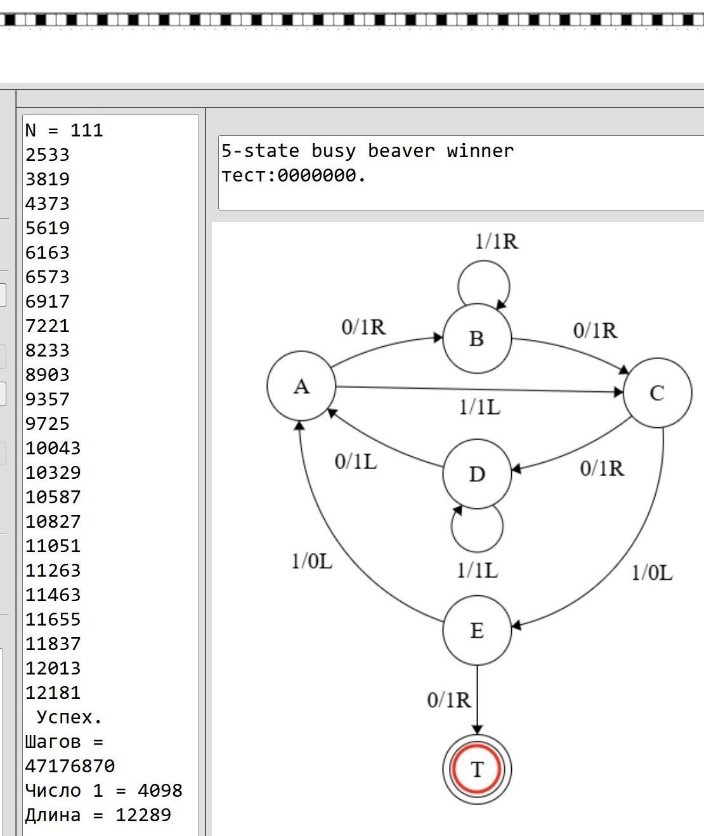
Рис.3. Диаграммы МТ для BB(5) и кандидата BB(6)
Fig. 3. MT charts for BB(5) and candidate BB(6)
Машина BB(5) останавливается через 47176870 шагов, и это можно промоделировать в программе. На рисунке для BB(5) показано заключительное состояние. В окне конфигураций через каждые 2 миллиона шагов указывается длина текущей цепочки, на ленте – часть последней цепочки длиной 111.
Для машин BB(6) и BB(7) значения функций S и настолько огромны, что для их определения найдены только нижние границы:
S(6) > (6) > 2 5 и S(7) > (7) > 2 112113 (запись больших чисел в нотации Д. Кнута).
Доказательство BB(5) потребовало не только больших вычислительных ресурсов, но и уникальных математических методов. Для некоторых МТ было использованы инструменты автоматизации доказательств, в частности, язык Lean (Lean, 2025).
В программе имеется доступ к базе данных из 10000 машин с шестью состояниями, для которых можно ставить задачи исследования их поведения.
Один из ведущих исследователей в области теории алгоритмов, Скотт Ааронсон, так отозвался о проблеме BB: «… изучение «бобров» делает философские открытия Гёделя и Тьюринга «количественными и конкретными». Мы больше не говорим абстрактно о «каких-то» пределах — мы пытаемся нащупать их руками. Найти машину Тьюринга, поведение которой непредсказуемо, — это всё равно что найти первую трещину в здании общепринятой математики» (Самая сложная задача математики, 2025).
По тематике проблемы BB достаточно много публикаций, и знакомство и ними может заинтересовать студентов и побудить к исследованиям.
Предполагается продолжить разработку программы FSMD для реализации следующих возможностей:
- генерация случайных диаграмм с заданными характеристиками (числом вершин, дуг, алфавита символов и т.п.);
- задание и сохранение набора тестовых цепочек для автоматов;
- решение задач по аналогии с программой JFLAB;
- решения задачи построения регулярного выражения по КА;
- автоматизация удаления пустых и недостижимых состояний в КА и МТ-автоматах;
- решение задачи удаления пустых переходов;
- реализация возможности генерации отчета по задаче построения автоматов;
- построение пространственно-временных диаграмм для МТ.
В заключение приведём краткий обзор результатов использования программы FMT в учебном процессе.
В течение учебного года 2024/25 в Финансовом университете были прочитаны лекции и проведены семинарские занятия по дисциплинам «Теория компиляции» и «Теория алгоритмов». В рабочих программах этих дисциплин предусмотрено решение задач на построение конечных автоматов и машин Тьюринга. Разработанная программа оказалась очень полезным инструментом: студенты легко осваивали работу в программе и справлялись с подобными задачами. На зачетах были предложены задачи, отличные от тех, что разбирались на занятиях. Некоторые студенты, в основном те, которые пропускали занятия или не были активными, понадеялись на помощь искусственного интеллекта (ИИ). Но они просчитались: при проверке решений легко обнаруживалось, что они этим пользовались. По условию задач результат должен был представлен в виде JSON-файла, который загружался бы в программу FSMD. Но ИИ, хотя и выдавал JSON, но формат не соответствовал требованиям программы. При использовании FSMD файл формируется автоматически в требуемом формате. Кроме того, в диаграммах от ИИ присутствовали склеенные дуги и неудачное размещение вершин. При запросе к ИИ можно было бы сформулировать уточняющие детали представления решений, но это требовало дополнительных усилий со стороны студентов.
Использование ИИ студентами носит массовый характер, и этому трудно препятствовать. Решение задач в любой дисциплине способствует не только лучшему усвоению материала, но и развитию логического мышления, приобретению полезных навыков в применении соответствующих инструментов. Студент, который вместо того, чтобы самостоятельно решать задачи, прибегает к помощи ИИ, не сможет освоить дисциплину в должной степени, получить новые знания и навыки. Поэтому правильно поставить его в условия, когда использование ИИ было бы затруднительным. Именно применение специализированных программ, подобных FSMD, позволяет это сделать. Решение задач в среде таких программ может быть обусловлено различными динамически настраиваемыми особенностями, которые ИИ не сможет учесть.