Введение
В настоящее время количество пользователей интеллектуальных ассистентов (как сейчас принято говорить, «искусственного интеллекта» - ИИ или «нейронных сетей») растёт лавинообразно. Значительная часть таких пользователей, не имея ни математической подготовки, ни опыта программирования, декларирует себя продвинутыми специалистами по ИИ. В результате создаются проблемы, обусловленные попытками некорректного применения доступных интеллектуальных средств, сомнительной интерпретацией и практическим использованием полученных результатов, а также вводящими в заблуждение пафосными заявлениями без реального содержания.
Это делает актуальным создание средств поддержки пользователя при работе с интеллектуальными ассистентами (ИА), в первую очередь, актуальна разработка средств автоматизации работы промпт-инженеров, обеспечивающих подготовку запросов к ИА.
В целом, результат взаимодействия субъекта с ИА определяется двумя факторами:
-
семантическим содержанием запросов или других текстов, предъявляемых ИА;
-
интеллектуальными возможностями самого ИА, которые могут варьироваться в широких пределах.
Неопределённость интерпретации семантического содержания запросов или других релевантных текстов, а также известная непредсказуемость реакции ИА на запросы затрудняют применение математического аппарата, требуя его существенной адаптации для нового контекста применения. В этой работе сделана одна из первых попыток такой адаптации. Для обеспечения компактного описания применяемых алгоритмов разработана специальная нотация.
Генерация правдоподобной, но неверной информации, называемая «галлюцинацией», пока является проблемой, сопровождающей практическое использование ИА. В частности, хорошо известно, что ИА может обосновать утверждения, взаимно отрицающие друг друга, если получит соответствующий запрос. Исключение составляют только строго обоснованные или очевидные наблюдаемые факты. Поэтому актуальным становится поиск инструментов, которые могут объективно оценивать корректность формулировок, вычисленных с помощью ИА.
Проблемы, рассмотренные в этой работе, стали особенно актуальными после 2020 года (Николенко и др., 2020), поэтому релевантных публикаций на тему автоматизации работы с ИА и устранения проблемы «галлюцинаций» относительно немного. Среди подходов, внушающих умеренный оптимизм, диалоговые методы, среди которых - «игра в дебаты» («Debate Game») (Irving и др., 2025) и генерация цепочек проверки (Chain-of-Verification Method) (Shehzaad и др., 2025), обеспечивающая устранение «галлюцинаций» путём запросов на обдумывание ИА собственных ответов и их самокоррекции. Однако эти подходы не опираются на значимый математический аппарат и безнадёжно далеки от полезного практического применения.
В этой работе представлены алгоритмы для решения двух задач:
-
генерации запросов, для которых аннотации (краткие описания ответов на запрос) наиболее близки к заданному описанию (решение обеспечивается эволюционным алгоритмом подбора запросов);
-
проверки корректности ответов интеллектуального ассистента (решение обеспечивается эволюционным алгоритмом проверки корректности ответов ИА, или «алгоритмом маятника»).
Основными компонентами указанных выше алгоритмов, определяющими вычисляемый результат, являются вновь разработанный квазигенетический алгоритм, обеспечивающий выполнение расширения множества запросов, и метод многомерного метрического шкалирования, строгое описание которого относительно редко встречается в публикациях. Квазигенетический алгоритм построен по аналогии с известным генетическим алгоритмом (Емельянов и др., 2003), применяемым для решения задач оптимизации и, в частности, для обучения нейронных сетей, с заменой операций кроссовера и мутации на выполняемые ИА операции псевдокроссовера и вариации, близкие по контексту применения, но принципиально другие по содержанию.
Основной принцип, реализуемый в применяемом подходе к решению задач, заключается в выполнении интеллектуальным ассистентом всех содержательных операций, связанных с извлечением количественных оценок из исследуемого материала, с последующим анализом этих оценок, применяя методы многомерного статистического анализа, технику проверки статистических гипотез и другие математические инструменты.
Инструментальные средства, работающие на основе приведённых далее алгоритмов, программно реализованы на базе OpenAI API. Эти средства в пилотном режиме работали с текстами психологического содержания, продемонстрировав убедительные результаты.
Наиболее очевидные перспективы практического применения представленные алгоритмы имеют там, где используются понятия со значительной вариативностью в интерпретации: в психологии, социологии, искусствоведении и других гуманитарных областях (Shoham и др., 2009; Николенко и др., 2020).
Статья предназначена для программистов, создающих средства для работы с большими языковыми моделями, и математиков, разрабатывающих методы практического использования возможностей искусственного интеллекта.
Применяемая нотация и основные понятия
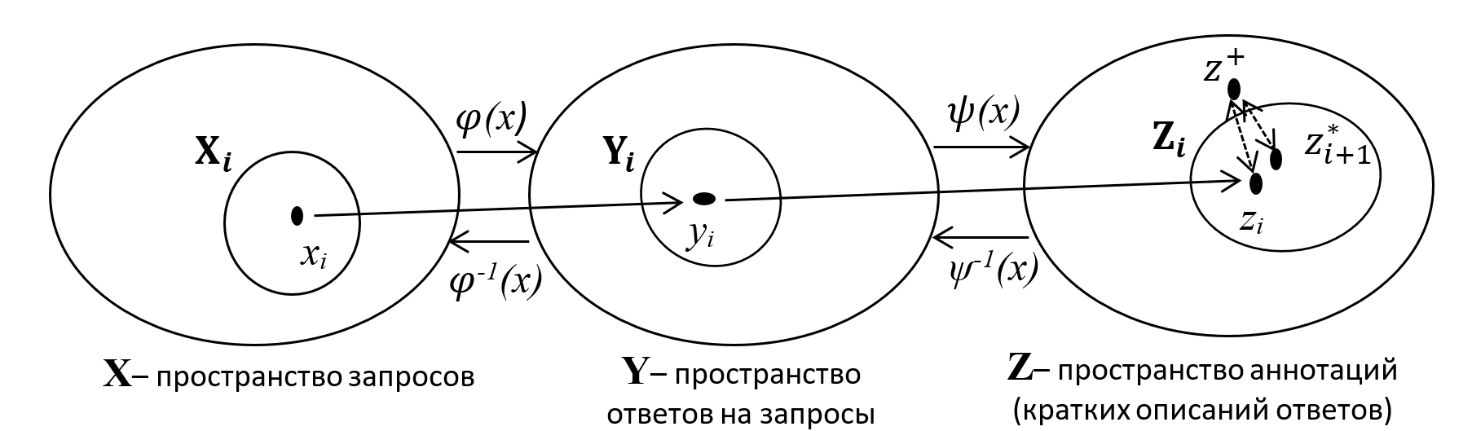
Рис. 1. Эволюционный алгоритм подбора запросов для ИА: операции над элементами метрических пространств
Fig. 1. Evolutionary prompt-selection algorithm for an intelligent assistant: operations on elements of metric spaces
X, Y и Z также используются как пространства шкалирования. Под расстояниями далее понимаются евклидовы расстояния. Квазирасстояния представляются значениями из числового отрезка [0;1] и вычисляются для заданных пар элементов метрических пространств X, Y и Z с помощью ИА как результаты запросов на сравнение элементов, входящих в заданные пары. Значение 1 соответствует полному совпадению содержания сравниваемых элементов, значение 0 – его полному несовпадению (очевидно, что результат сравнения неоднозначен и определяется особенностями применяемых ИА). В запросах к ИА явно указывается требование сделать сравнение предъявляемых элементов, выразив результат вещественным числом из интервала.
- заданная аннотация (краткое описание ответа на запрос).
Операции в метрическом пространстве X:
i++ и j++ - увеличение индексов i и j на единицу;
Эволюционный алгоритм подбора запросов для ИА
Задача формулируется следующим образом.
Алгоритм решения:
-
Задать множество базовых запросов . . и для всех элементов множеств и . .
-
Если , то вычислить ИА-отображения и для всех элементов множеств и .
-
Найти медиану Кемени и образы её отображений и .
-
Вычислить расширение применив квазигенетический алгоритм.
-
Вычислить матрицы , и .
-
Вычислить , и , пометив полученные взаимные расстояния между элементами множеств , и .
-
Найти медиану Кемени .
-
Определить окрестность запроса , используя взаимные расстояния, определяемые матрицей ;
-
Вычислить ИА-отображения для всех элементов окрестности запроса .
-
Проверить условие . Если условие выполнено, то , удалить заданную относительную часть элементов и их прообразов и и переход к шагу 11, иначе переход к шагу 4.
-
Вычислить .
-
Если , то и останов, иначе переход к шагу 13.
-
.
-
i++.
-
Переход к шагу 2.
Квазигенетический алгоритм для выполнения расширения множества запросов при выполнении операций
-
Задать множество базовых запросов . j=0.
-
Проверить условие . Если условие выполнено, то переход к шагу 3, иначе останов.
-
Квазигенетический отбор элементов множества на итерации j по «правилу рулетки» с использованием в качестве функции качества расстояния , где
-
Формирование дополнения к множеству путём применения к элементам множества операций псевдокроссовера , и , а также псевдомутации .
-
Объединение множества запросов , соответствующего итерации j, и дополнения : .
-
j++.
-
Переход к шагу 2.
Сходимость вычислительной процедуры определяется условием, указанным на шаге 10 её описания, результат проверки которого, в свою очередь, зависит от семантического содержания запросов, предъявляемых ИА, и интеллектуальных возможностей самого применяемого ИА.
Эволюционный алгоритм проверки корректности ответов ИА
Основной тезис: корректные по содержанию ответы на запросы ИА значимо лучше согласованы между собой, чем ответы, некорректные по содержанию.
-
Получить необходимый для анализа содержательный материал в ответ на порождающий запрос или задать непосредственно. i=0. . .
-
i++.
-
Вычислить .
-
Если i - чётное, то и , иначе и .
-
Вычислить .
-
Вычислить дисперсии и .
-
При условии нормальности распределений расстояний до центроидов и , проверить нулевую гипотезу о равенстве дисперсий и , используя F-тест для статистики , если , или для статистики , если . Если нулевая гипотеза F-теста о равенстве дисперсий не отвергается и , то переход к шагу 2, иначе переход к шагу 8.
-
Если нулевая гипотеза о равенстве дисперсий отвергнута, то, если , сделать вывод о корректности исследуемого содержательного материала , или, если , сделать вывод о корректности отрицания исследуемого содержательного материала , иначе считать корректность указанного материала неустановленной.
Сходимость рассматриваемой вычислительной процедуры определяется условием, указанным на шаге 7 её описания, результат проверки которого, в свою очередь, зависит от семантического содержания порождающего запроса к ИА (или исходного исследуемого содержательного материала) и интеллектуальных возможностей самого применяемого ИА.
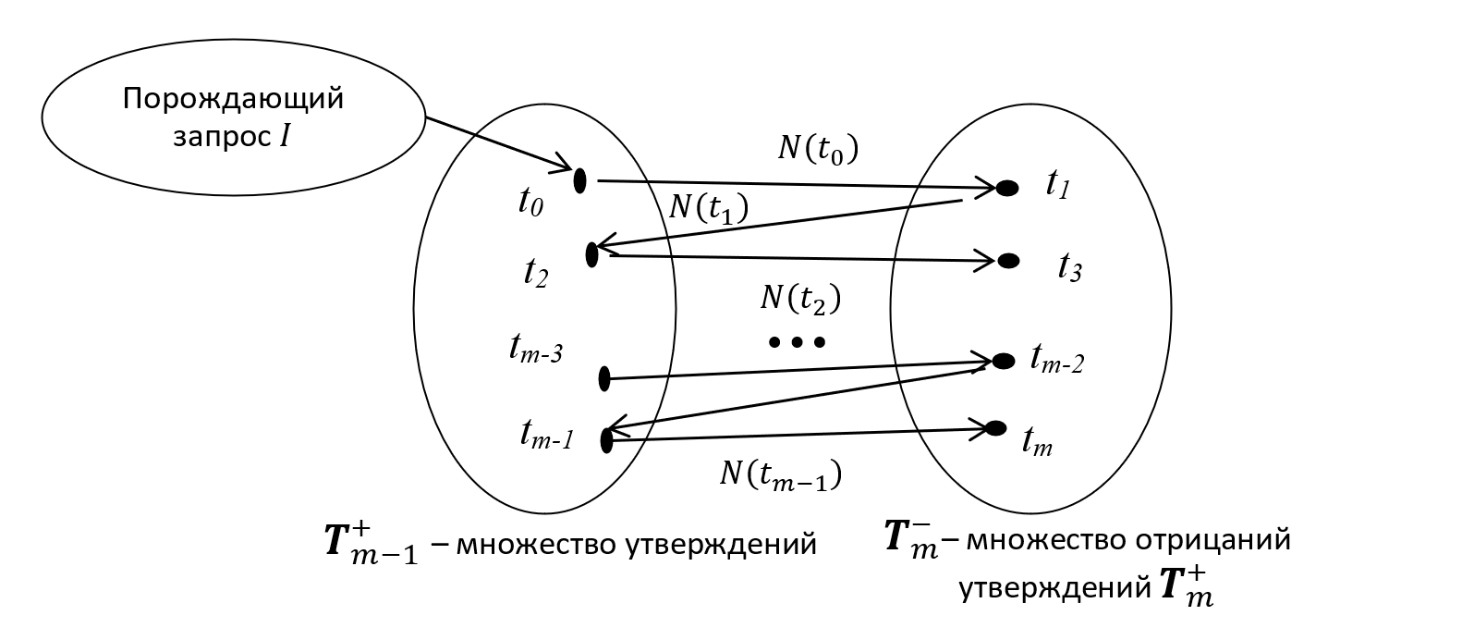
Рис. 2. Алгоритм маятника: операции над элементами множества утверждений и множества отрицаний утверждений
Fig. 2. Pendulum algorithm: operations on elements of the set of statements and the set of their negations
В качестве событий, в частности, может рассматриваться нахождение множеств точек, представляющих утверждения и их отрицания, в определённых областях пространства шкалирования или распределение определённых конфигураций точек, соответствующих исследуемым классам признаков, по заданным областям этого пространства (Kuravsky, 2014; Kuravsky, Greshnikov и др., 2024; Kuravsky, Orishchenko и др., 2025; Куравский, Юрьев и др., 2024).
Метод многомерного метрического шкалирования Торгерсона
Алгоритм многомерного метрического шкалирования Торгерсона
-
Вычислить матрицу квадратов квазирасстояний
-
Вычислить матрицу взаимных скалярных произведений (матрицу Грама) , где - матрица двойного центрирования, — единичная матрица размера , — вектор-столбец из единиц, — вектор-строка из единиц (умножение на матрицу центрирует матрицу, вычитая из каждого её элемента среднее по строке и среднее по столбцу и добавляя общее среднее).
-
Решить алгебраическую проблему собственных значений, вычислив спектральное разложение , где ) - диагональная матрица собственных значений, упорядоченных по убыванию ( ), – матрица соответствующих им собственных векторов, расположенных по столбцам.
-
Вычислить -координатное представление элементов заданного множества в линейном евклидовом пространстве размерности , определив матрицу , где ) - диагональная матрица квадратных корней из наибольших собственных значений матрицы , упорядоченных по убыванию, - матрица первых координат собственных векторов матрицы , расположенных по столбцам (т.е., первых срок матрицы ; координаты элементов множества в матрице размера также расположены по столбцам).
Следует заметить, что:
-
Матрица Грама является симметрической и положительно полуопределенной, что позволяет представить её в виде ; один из способов вычисления матрицы координат рассмотрен выше;
-
Доказано, что приведённый алгоритм обеспечивает вычисление решения, обеспечивающего наименьшее значение критерия ;
-
Величина равна нулю при
-
Всли - ортогональная матрица размера и - некоторое -координатное решение задачи, обеспечивающее наименьшее значение критерия , то – равноценное решение, обеспечивающее то же самое наименьшее значение критерия .
Результаты
Генерация запроса, для которого аннотация наиболее близка к заданному описанию
В приведённых далее запросах сохранён индивидуальный стиль формулировок, подготовленных опытным промпт-инженером.
Что такое бихевиоральный подход?
Как изучается поведение в психологии?
Какие методы используются для анализа поведения?
Что такое объективное изучение поведения?
Для решения задачи применялся ИА ChatGPT [gpt-4o-mini].
«Создай новый запрос, объединяющий идеи из следующих двух запросов.»
«Создай КРАТКИЙ новый запрос, выделяя общие ключевые идеи из следующих двух запросов. Запрос должен быть лаконичным (не более 2-3 предложений).»
«Создай КРАТКИЙ новый запрос, дополняя первый запрос элементами из второго. Запрос должен быть лаконичным.»
«Переформулируй следующий запрос КРАТКО, сохраняя его смысл»
«Оцени семантическое расстояние между двумя текстами по шкале от 0.00 до 1.00 как меру различия их основных утверждений. Будь строгим: не занижай расстояния, учитывай различия в деталях, уровне абстракции, примерах и выводах. Если один текст даёт общее описание, а другой — конкретную теорию или пример, расстояние должно быть повышенным, даже при тематической близости. Верни только одно число с двумя знаками после запятой, без какого-либо дополнительного текста.»
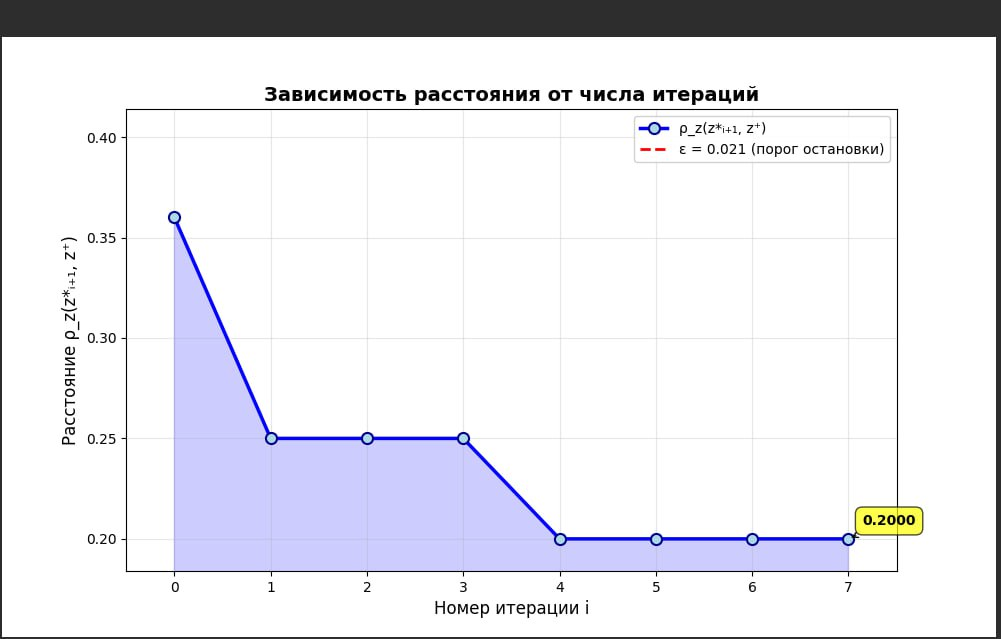
Проверка корректности тезиса, используя алгоритм маятника
В приведённых далее запросах сохранён индивидуальный стиль формулировок, подготовленных опытным промпт-инженером.
В качестве исследуемого тезиса использовалась фраза «Культурно-историческая психология построена на основе марксистской теории».
«Ты — эксперт в области философии, психологии и методологии науки. Сформулируй чёткий, аргументированный тезис H на заданную тему, который можно как подтверждать, так и опровергать; его правдоподобность далее будет проверяться по компактности кластеров подтверждающих и опровергающих аргументов в пространстве смыслов. Ответ должен иметь логическую структуру (тезис, обоснование, вывод), быть конкретным и лаконичным (3–5 содержательных предложений).»
Результат 1
«Культурно-историческая психология построена на основе марксистской
теории.
Обоснование: Основоположник культурно-исторической психологии Лев
Выготский использует идеи Маркса о социальном контексте в развитии индивида,
подчеркивая, что психологические процессы формируются в результате социального
взаимодействия и исторических условий. Он акцентирует внимание на роли культуры
и языка в когнитивном развитии, что согласуется с марксистской концепцией о
влиятельности социальной среды на личность.
Вывод: таким образом, можно утверждать, что культурно-историческая психология во многом опирается на марксистские идеи, что подтверждается анализом ключевых понятий и принципов, заложенных в обоих подходах.»
«Ты работаешь с цепочкой теоретических высказываний.
Сформулируй новое самодостаточное высказывание (1–2 предложения), которое по смыслу противоречит данному тексту, но остаётся в рамках исходной темы и той же предметной области, сохраняя ключевые понятия и изменяя только отношения между ними.
Не используй метаязык (типа “аргумент”, “тезис”, “это утверждение/текст”), не пересказывай и не цитируй исходный текст, не предлагай компромиссов “с одной стороны… с другой стороны”.
Верни только текст нового высказывания, без пояснений.»
Результат 2
«Культурно-историческая психология не может быть сведена к марксистским идеям,
так как ее основные принципы, разработанные Львом Выготским, подчеркивают
уникальность культурных факторов и индивидуального развития, значительно
отличаясь от марксистского акцента на классовой борьбе и экономических условиях.
На самом деле, понимание когнитивного развития напрямую вытекает из специфики
культурного контекста, а не из марксистской теории о влиянии социальной среды.»
Текст запроса 3 совпадает с текстом запроса 2.
Результат 3
«Культурно-историческая психология тесно связана с марксистскими идеями, поскольку акцент на социальных условиях и взаимодействии подчеркивает, что как индивидуальное развитие, так и когнитивные процессы невозможно понять без учета экономических и социальных факторов, описанных в марксизме. Таким образом, понимание этих процессов действительно зависит от анализа социальных структур и классовых отношений, важность которых существенно перекрывает роль уникальных культурных факторов.»
Текст запроса 4 совпадает с текстом запроса 2.
Результат 4
«Культурно-историческая психология может быть понята вне марксистской теории, так как она акцентирует внимание на уникальных культурных факторах, формах общения и языковых практиках, которые формируют когнитивные процессы независимо от экономических и социальных условий. Таким образом, развитие индивида и его психология могут быть исследованы без необходимости опираться на классовые отношения или социальные структуры, что подчеркивает разнообразие влияний на личность и стиль мышления.»
«Оцени семантическое расстояние между двумя текстами по шкале от 0.00 до 1.00 как меру различия их основных утверждений. Будь строгим: не занижай расстояния, учитывай различия в деталях, уровне абстракции, примерах и выводах. Если один текст даёт общее описание, а другой — конкретную теорию или пример, расстояние должно быть повышенным, даже при тематической близости. Верни только одно число с двумя знаками после запятой, без какого-либо дополнительного текста.»
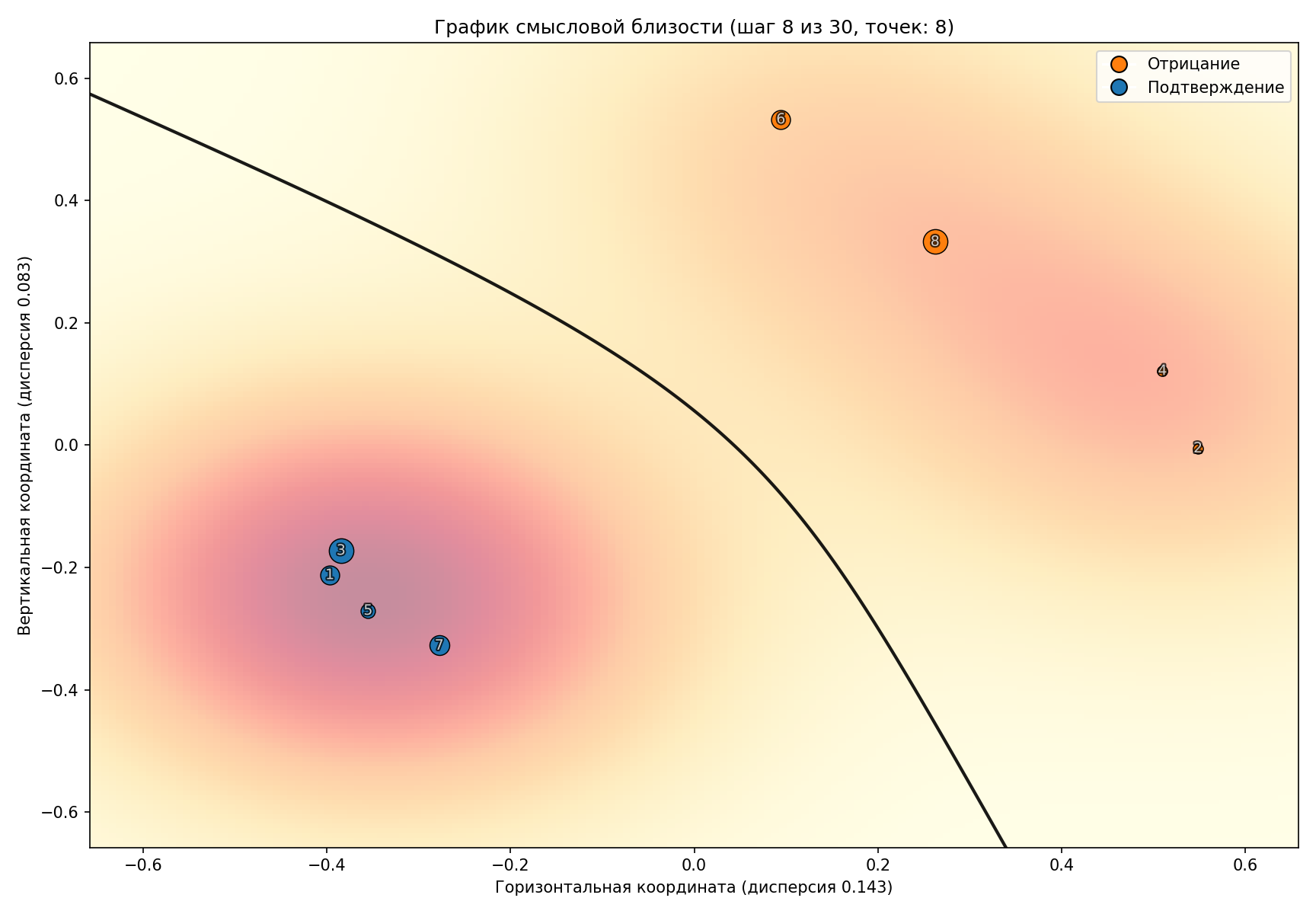
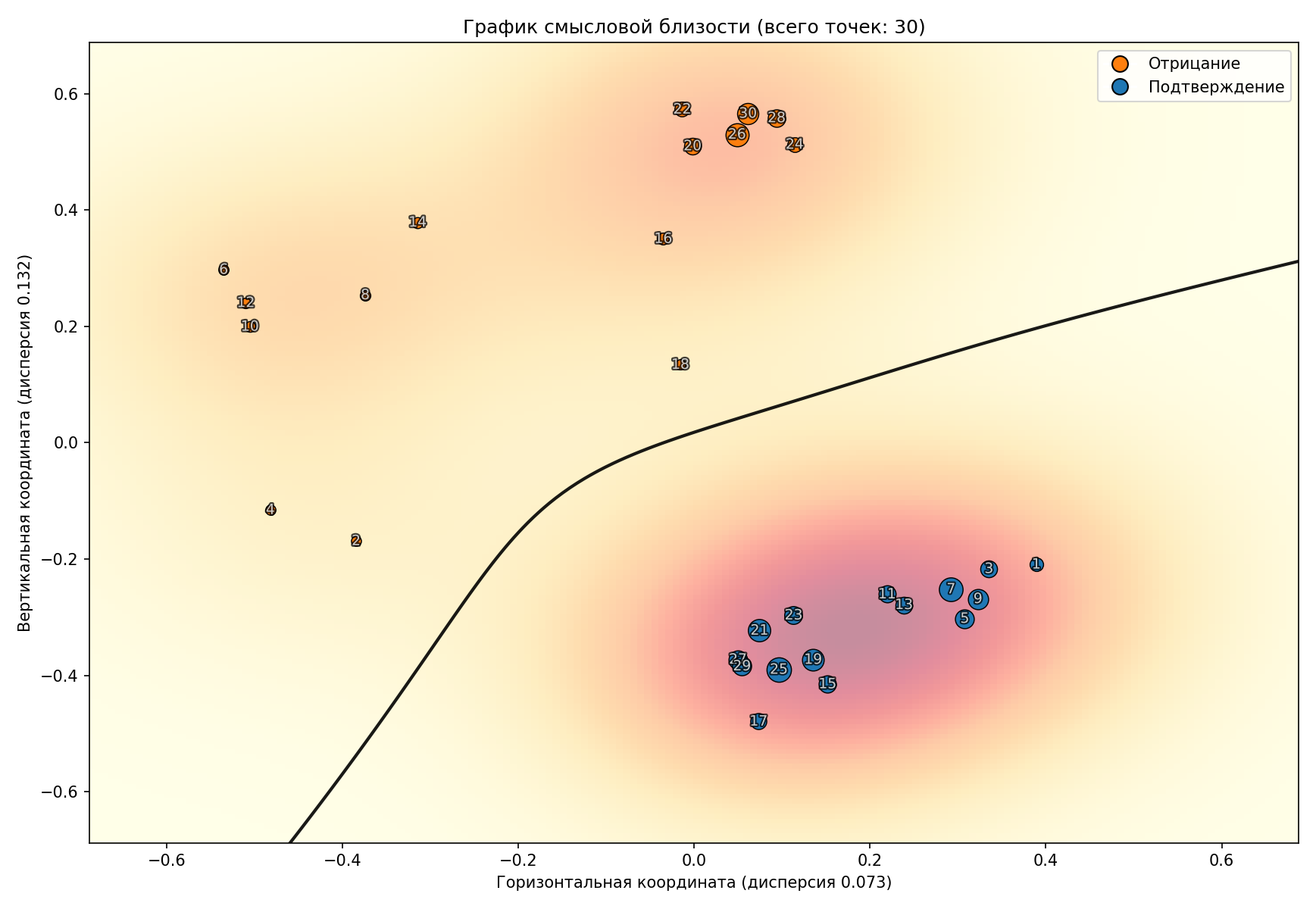
Продолжительность вычислений на компьютере среднего быстродействия (базовая тактовая частота процессора – 2,70 ГГц) составило 71 секунду, средняя продолжительность отработки одного запроса к ИА - 2,34 сек.
Дополнительное наблюдение: сужение цепочки к семантическому ядру противоречия
-
«Индивидуальный опыт и уникальные культурные формы рассматриваются как значимый индикатор когнитивного развития.»
-
«Индивидуальный опыт трактуется как субъективная основа, недостаточная без анализа социальных и структурных условий.»
Это наблюдение позволяет рассматривать алгоритм маятника как инструмент, автоматически выявляющий смысловую основу, вокруг которой происходит спор по заданной теме.
Заключение
- Результат взаимодействия с ИА определяется двумя факторами: семантическим содержанием запросов или других текстов, предъявляемых ИА, и интеллектуальными возможностями самого ИА, которые могут варьироваться в широких пределах.
- Основной принцип, реализуемый в применяемом подходе к решению задач, заключается в выполнении интеллектуальным ассистентом всех содержательных операций, связанных с извлечением количественных оценок из исследуемого материала, с последующим анализом этих оценок, применяя методы многомерного статистического анализа, технику проверки статистических гипотез и другие математические инструменты.
- Разработаны эволюционный алгоритм генерации запросов для ИА, аннотации ответов на которые наиболее близки к заданным описаниям, и эволюционный алгоритм проверки корректности ответов интеллектуального ассистента.
- Основой эволюционного алгоритма генерации запросов является квазигенетический алгоритм, который обеспечивает выполнение расширения множества запросов. Квазигенетический алгоритм построен по аналогии с известным генетическим алгоритмом, применяемым для решения задач оптимизации и, в частности, для обучения нейронных сетей, с заменой операций кроссовера и мутации на выполняемые ИА операции псевдокроссовера и вариации, близкие по контексту применения, но принципиально другие по содержанию.
- Алгоритм маятника позволяет выявлять смысловую основу, вокруг которой происходит спор по заданной теме.
- Для обеспечения компактного описания эволюционных алгоритмов разработана специальная нотация.
- Доказана сходимость эволюционного алгоритма генерации запросов при определённых условиях (представленных на шаге 10 описания алгоритма), результат проверки которых задаётся семантическим содержанием запросов, предъявляемых ИА, и интеллектуальными возможностями самого применяемого ИА.
- Сходимость эволюционного алгоритма проверки корректности ответов определяется условием, указанным на шаге 7 её описания, результат проверки которого зависит от семантического содержания порождающего запроса к ИА (или исходного исследуемого содержательного материала) и интеллектуальных возможностей самого применяемого ИА.
- Доказано, что при достаточно больших количествах событий даже разовое проявление некоторой закономерности фактически свидетельствует о её наличии. В качестве таких событий может рассматриваться нахождение множеств точек в определённых областях пространства шкалирования.
- Пилотное применение разработанных алгоритмов для решения психологических задач показало их эффективность и семантическую корректность.