С. Ю. Прошлый урок закончился тем, что мы доказывали, что произведение двух чисел не зависит от того, в каком порядке их умножать. Мы доказывали, что 2 х3 и 3 х2 - одно и то же. Мы сейчас поупражняемся немножко, а потом докажем, что произведение двух чисел не зависит от того, в каком порядке перемножать эти числа. К доске пойдет Паша Павлов. Напиши, Паша X х4. Нужно нарисовать схему к этому выражению. Скажи, пожалуйста, Славочка, что здесь умножается, X или 4?
Слава. X, конечно.
С. Ю. X, конечно. Садись, правильно. Сколько раз нужно взять число X, Сережа?
Сережа. 4.
С. Ю. Правильно, Сережа.
Паша рисует схему:
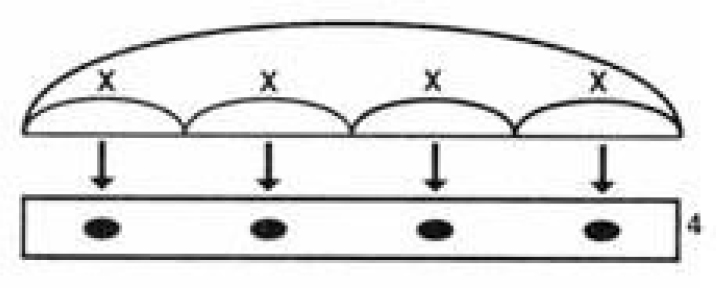
С. Ю. Очень важную вещь сделал Паша Павлов. Он стал обозначать все вместе не в уравнениях, а в выражениях. Садись, Паша. А теперь надо подумать, что же поставить здесь (показывает). Это не уравнение, у нас нет конкретного числа.
Юля. х х 4.
Лена. х + 4.
С. Ю. Два варианта у нас есть: Вариант Юли: х х4 - и вариант Лены: х + 4. Давайте обсудим, кто из них прав. Кто докажет, что надо ставитьх х4, ах + 4- ошибка?
Юля. Потому что в выражении не х + 4. Если х + 4, то совсем другая схема будет.
С. Ю. Согласен. А кто нарисует схему к выражению х + 4, чтобы стало ясно, что х + 4 здесь нельзя ставить.
Юля рисует:

С. Ю. Только возьми тот же самый х, что на схеме I, у Паши.
Юля. А 4 тогда как рисовать?
С. Ю. А вот это страшно интересный вопрос. Поставить х легко, он тот же самый, а вот как 4 поставить? Мы не знаем, чему равна здесь единица, поэтому 4 можно поставить любым. Теперь у нас две схемы: х х4 и х + 4. Вот, это - х, а рисуется как угодно, потому что мы не знаем, чему равна единица. У нас здесь единица равна вот этому (показывает). Кто может пойти к доске и найти единицу? Леночка, пожалуйста. (Лена делит отрезок, равный 4, на 4 части.) Правильно. Вот этот кусочек - это единица Четвертая часть четверки. Ирине Ефимовна, у вас взгляд очень возмущенный, чем вы возмущены?
И. Е. Конечно, я возмущаюсь. Если ли мы выяснили, что этот отрезок равен единице, то тогда вот этот отрезок чему равен?
Дети. Двойке.
И. Е. У нас получилось, что х равен двум единицам, а ведь неизвестно, чему равен х. Его нельзя рисовать заведомо равным двум. Поэтому я не знаю, как можно сделать схему; на которой одновременно будет их, и 4. Чтобы было одновременно показано, что х равен неизвестно чему, а второй отрезок на этой схеме равен 4.
Голос. Нам надо узнать, чему равен х, тогда нарисуем.
И. Е. Да, но если у нас выражение с х неизвестным, то непонятно, как рисовать.
С. Ю. Вы, Ирина Ефимовна, предлагаете вообще не рисовать схемы к таким выражени-
ям?
И. Е. Нет, почему. Есть, например такой вариант:

X рисовать в виде отрезка с разрывом. Неизвестно, чему он равен. Нарисовать его с разрывом, т. е. нарисовать такой отрезок, который может сжиматься и растягиваться в зависимости оттого, чему равен х.
С. Ю. Это очень красиво, очень остроумно.
Голос. А почему 4 без разрыва?
И. Е. Но 4 нам же известно, чему равно. Этот отрезок фиксированный, мы знаем, чему
он равен.
Дети. Четырем.
И. Е. А этот отрезок (х) неизвестен.
С. Ю. Идея Ирины Ефимовны заключается в том, чтобы х всегда рисовать особым обра-
зом. Мне эта идея очень нравится. Особым образом, показывая, что х нам неизвестен. Его
нельзя нарисовать обыкновенным отрезком. Например, если я нарисую так:

С. Ю. Чему он равен?
Дети. Двум.
С. Ю. А если я нарисую так:

С. Ю. Чему он будет равен?
Дети. Трем.
С. Ю. Правильно, т. е., каким бы я ни нарисовал х - большим, маленьким, я его рисую не иксом, а чем?
Дети. Ответом.
С. Ю. Ответом, очень точно. И вот Ирина Ефимовна предлагает нам из этого интересного положения выйти так. В первой схеме у нас нет конкретного числа на схеме. Конкретное число живет здесь, в домике, а на схеме его нет. Поэтому не страшно, можно рисовать х. А если мы на той же схеме, где х, поставим конкретное число, любое число, то мы разделим его на него самого и получим единицу. И х здесь получается двойка, а это неправильно, мы не знаем, чему оно равно. Ирина Ефимовна предлагает: там, где на схемах стоит конкретное число, х рисовать с разрывом. Вот эти точки означают, что х не такой, как здесь изображен, а мы не знаем, какой, может быть, больше, а может быть, меньше. X меняется. Я бы представлял себе его в виде пружинки или резиночки, которая может сжиматься или растягиваться.
Дети. Как жвачка.
С. Ю. Правильно, вот жвачка может сжиматься и растягиваться. И х - это такая жвачка. А жвачку как нарисовать? Ее нарисовать очень трудно. Нарисуйте, дети, жвачки. Света, нарисуй жвачку. Не показывай, нарисуй. Нарисуй, Юля.
Все рисуют:
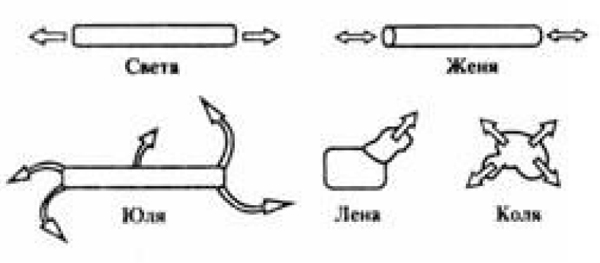
С. Ю. Посмотрите, почему так нарисовала жвачку Света, что означают эти стрелочки?
Света. Эти стрелочки значат, что она растягивается.
С. Ю. Что ты нарисовала, Юля?
Юля. Я нарисовала жвачку, а эти стрелочки показывают, что она может в разные сторо-
ны растягиваться, совсем в разные.
Женя. А она лопнет.
Юля. Есть такие жвачки, которые не лопаются.
С. Ю. Юля показывает, что можно жвачку не просто растягивать, как у Светы или у Жени, а можно тянуть, и сюда тянуть, и сюда, и сюда (показывает). А у Светы эти стрелочки не означают, что можно сюда потянуть, сюда и сюда, а просто, что можно тянуть. У Светы можно тянуть туда и сюда, а у Юли и сюда, и сюда, и сюда в разные стороны она растягивается.
Лена поднимает руку.
С. Ю. Иди, Лена, нарисуй. (Лена рисует.) Вот как интересно. Нарисован квадратик, а потом в какую-то штуку превращается. Объясни.
Лена. Эту жвачку можно растянуть, вытянуть из квадратика и обратно собрать.
С. Ю. А какая она была вначале, покажи. (Лена рисует квадратик.) Смотрите, вначале была такая жвачка, квадратная. Обыкновенный квадратик, никакая не жвачка, как наше обыкновенное число. А теперь ее можно менять, вытягивать и обратно загонять в квадрат. А теперь скажите, пожалуйста, если сравнить вот это (что нарисовала Ирина Ефимовна) и вот, это (жвачки) - это одно и то же? Или нет?
Дети. Да, одно и то же.
С. Ю. Я прошу вас нарисовать рядом вот такой х (отрезок) и вот такую жвачку - квадратиком, которую можно тащить, во что угодно превращать и загонять обратно в квадратик. Интересно, чем отличаются эти схемы и что в них общего? В той, что предлагала Ирина Ефимовна для описания неизвестного х, и в рисунках жвачки. Разные это вещи или это одно и то же? Пожалуйста, Коля. Коля подходит к схеме.

Коля. Вот эта единица - вот она вся (показывает весь отрезок).
С. Ю. Вот и поработали со жвачками. Коля предлагает вернуться обратно и говорит, что эта схема правильная, только единица не это, а всё - единица, весь отрезок - единица. Он предлагает назвать единицей всё в целом, всё, что является конечным итогом. Так, Коля?
Коля. Да.
С. Ю. Тебя не смущает, что вот это один (показывает весь отрезок), а внутри его 4?
Коля. Нет, не смущает.
Юля. Если это один, то почему же здесь 4?
С. Ю. Непонятно, что означает один. Здесь масса важных и очень нужных вопросов. Первый вопрос: почему 4 находится внутри единицы? 4 же больше, чем единица? Вопрос второй: если это 4, то вот это (показывает 1/4 от этой 4) тоже один. Странная вещь, две единицы и они разные. Это одно и то же - это один и это один:

С. Ю. Или нет?
Дети. Нет.
С. Ю. Коля, ответь на два вопроса.
Коля. Вот + 4, четверка прибавляется, а вот один - вот какой большой.
С. Ю. 4 меньше единицы, да?
Коля. Да.
С. Ю. Спасибо. Коля говорит, что х + 4 и все это вместе - единица, конечно, эта единица больше, чем какая-то четверка. Коля на второй вопрос не ответил. А вот эта единица, которая четвертушка четверки, и эта большая единица - они тоже разные?
Коля. Они одинаковые.
С. Ю. А тебя не смущает, что одна вот такая большая, а другая вот такая маленькая. Почему?
Коля. Потому что вот это (показывает скобку на схеме) все круглое. Единица круглая.
С. Ю. Почему она круглая?
Коля. Закругленная, целая.
С. Ю. Коля говорит, что эта штука не просто скобочка, а обозначает, что она целая, закругленная. Это все целое. И целое в каком-то смысле действительно закругленное. А все остальное - его части. Так вот для Коли это круглое - единица, т. е. все целое. Ответь на второй вопрос: вот эта единичка и вот эта единица - разные или одинаковые?
Коля. Одинаковые.
С. Ю. Почему? Я вижу глазом, что разные - маленькая и большая.
Коля. Потому что это тоже круглая, только меньше.
С. Ю. Это уменьшенная копия той единицы, да?
Коля. Да.
С. Ю. Можно ли сказать так, Коля, что никаких чисел нет, есть только единицы?
Коля. Можно.
С. Ю. Все числа - единицы. Есть вот такая единица, такая (показывает разной длины отрезки), и они все целенькие и закругленные. Каждое число - единицы. Они все-единицы. Это ты хочешь сказать, Коля?
Коля. Да.
С. Ю. Это очень правильно, по-моему. Абсолютно верно. Но мне интересно сюда вернуться, к этим схемам. Они разные или одинаковые (схемы с отрезком и со жвачкой)?
Дети. Одинаковые.
Голос. Разные.
С. Ю. И я считаю, что они разные. Это совершенно очевидная вещь, дети. Как вы боитесь сказать, в отличие от Коли, то, чего никто не думает. Если 5 человек закричали, что одинаковые, то уже никто не скажет, что разные.
Женя. Схемы разные, потому что та схема, схема х, она длинная, а эта - квадратная.
С. Ю. Эта схема про длину, а эта - про площадь.
Лена. Вот эта вот жвачка (схемаЖени), она тоже объемная, тут я тоже вижу объем.
С. Ю. Ну как ты видишь объем? Нарисуй.
Дети. Он не рисуется.
С. Ю. Такой объем, который не рисуется? Объем можно нарисовать.
Рисует:

С. Ю. Вот этот X у нас будет как палочка, но прерывистая. То сжимается, то разжимается.
Дети. Сигарета.
С. Ю. Вы это имели в виду или другой какой-то?
Надя. Другой.
С. Ю. Какой другой? Нарисуй. Надя считает, что можно так дорисовать схему Ирины Ефимовны, чтобы получилась как жвачка.
Надя рисует.
Коля. Можно растянуть эту жвачку, и получится отрезок.
С. Ю. У Коли та же мысль, что и у Лены, только выражена более строго математически. У Лены можно тянуть только этот кусок. А Коля говорит, что можно брать этот столбик и растягивать его в блин, как тесто катают. Его можно и так тянуть, и так сжимать, а можно не сжимать, не растягивать, а катать, т. е. делать плоским. Поэтому стрелочки надо так поставить: и туда, и сюда... Теперь мы выяснили точно с помощью Леночки и Коли различие этих схем. Первая схема говорит, что х можно уменьшать или увеличивать, и всё. А здесь можно х уменьшать, увеличивать, можно делать совсем другим. Можно из длинного делать плоское. Превращать длину в объем. Это очень тонкое замечание. Действительно, такой х совсем другой. Здесь длина переходит в длину, а здесь она переходит в объем, точнее, в площадь1.
Данный урок был впервые опубликован в книге: Берлянд И. Е., Курганов
С. Ю. Математика в Школе диалога культур. Кемерово: «АЛЕФ» Гуманитарный Центр, 1993.
1 Урок проводил С.Ю. Курганов.