К проблеме оценки метапредметной компетентности испытуемых

 В связи с принятием в 2009 г. в Российской Федерации нового Федерального государственного стандарта общего начального образования второго поколения, ориентированного на компетентностный подход к оценке качества образования, остро встал вопрос о проектировании методик диагностики образовательных результатов учащихся [7]. В Московском городском психолого-педагогическом университете проводится разработка и экспериментальная проверка пакета диагностических методик оценки метапредметных образовательных результатов учащихся начальной школы. К метапредметным результатам обучающихся относятся освоенные ими универсальные учебные действия (познавательные, регулятивные и коммуникативные), которые обеспечивают овладение ключевыми компетенциями, составляющими основу умения учиться, и межпредметные понятия. Разрабатываются задания для массового обследования выпускников начальной школы.

В рамках этих работ нами была предпринята попытка спроектировать диагностические задания, нацеленные на проверку таких метапредметных компетенций выпускников начальной школы, как использование знаково-символических средств представления информации для создания моделей изучаемых объектов и процессов, схем решения учебных и практических задач. В настоящей статье анализируются результаты экспериментальной проверки двух диагностических заданий закрытого типа для оценки понимания выпускниками начальной школы пространственных отношений объектов, изображенных на схематическом рисунке. При проектировании заданий мы исходили из развитого в научной школе В.В.Давыдова понимания психологической природы метапредметных компетенций как формы теоретического мышления, проявляющегося при решении различных предметных задач[1; 2; 3; 5]. Как показывает опыт проектирования контрольно-измерительных методов в образовании, для оценки метапредметных компетенций желательно использовать задания разной предметной сложности [1;           4].

Предполагается, что для решения более сложных предметных задач обычно требуется более высокое развитие метапредметных компетенций.

В заданиях закрытого типа обычно дается насколько вариантов ответа на поставленный вопрос. Испытуемому предлагается выбрать один правильный вариант ответа. Такой тип диагностических заданий удобен при обследовании большого количества испытуемых и обработке этих данных. Вместе с тем всегда возможен случай, когда испытуемый не будет решать поставленную задачу, а попробует угадать верный ответ. В этой связи возникает проблема оценки компетентности испытуемого по результатам выбора правильного ответа в заданиях заведомо разной сложности. В частности, возникает вопрос, можно ли более сложной предметной задаче придать заведомо больший вес, чем менее сложной, при подсчете баллов по совокупности решения всех задач диагностической методики.       Мы исходим из того, что этот вопрос надо решать по результатам экспериментальной проверки конкретных заданий.

Рассмотрим два задания. Они основаны на проверке понимания схематичного изображения некоторой пространственной ситуации. Сами изображения стилизованы под детские рисунки. Появление этих рисунков объяснено в задании как результат действия некоторых учеников. Это позволяло, образно говоря, уменьшить возможный страх ученика перед этими довольно трудными заданиями.

Задание 1. Ваня наблюдал за тренировкой бегунов на стадионе. Спортсмены бежали строго друг за другом, не отставая. Ваня нарисовал момент, когда некоторые спортсмены оказались за плакатом (рис.1). Сколько всего спортсменов было на беговой дорожке? Выбери один правильный ответ! Варианты ответов: а) 5 человек; б) 7 человек; в) 8 человек; г) не могу точно сказать.

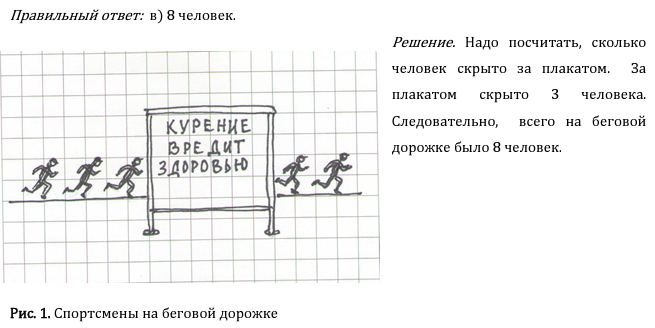
Решение. Надо посчитать, сколько человек скрыто за плакатом. За плакатом скрыто 3 человека. Следовательно, всего на беговой дорожке было 8 человек.

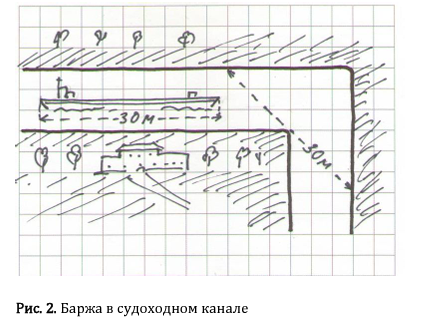
Задание 2. Сережа нарисовал, как баржа плывет по каналу (рис.2). Канал изображен сверху, баржа изображена сбоку. Длина баржи - 30 м. Ширина баржи 5 м. Ширина канала на повороте, как показано на рисунке, - 30 м. Может ли баржа пройти поворот? Выбери один правильный ответ! Варианты ответов: а) может пройти; б) не может пройти; в) может пройти впритирку к берегу; г) не могу точно сказать.

Правильный ответ: б) не может пройти.

Решение. Нужно представить себе вид баржи сверху, так же, как мы смотрим на канал. Тогда становится ясно, что ширины канала на поворот баржи не хватает.

В обоих заданиях ученику надо было продемонстрировать умение представить себе с помощью схематичного рисунка и текстового описания отношения между величинами пространственных объектов. При этом задания существенно различались по трудности. Если в задании 1 достаточно было «прочитать» заданные в рисунке пространственные отношения, то в задании 2 надо было продемонстрировать еще умение трансформировать чертеж, т. е. действовать в двух планах пространственного отображения реальности, что значительно труднее. Проблема заключается в следующем вопросе: можно ли второму заданию придать больший вес, чем первому?

В соответствии с этим было выдвинуто две гипотезы.

Первая гипотеза: задание 2 более трудное, чем задание 1.

Вторая гипотеза: задание 1 и задание 2 между собой связаны; успешное выполнение задания 1 является условием выполнения задания 2.

Если обе гипотезы подтвердятся, то заданию 2 можно будет придать больший вес. Например, в случае решения задания 1 испытуемый получает 1 балл, а в случае решения задания 2 - 2 балла. Итого в сумме можно получить 3 балла.

Результаты экспериментальной проверки

Проверка первой гипотезы. Наши задания проходили экспериментальную проверку в числе других диагностических заданий на контингенте выпускников начальных классов школ Центрального административного округа Москвы1. В табл. 1 представлены результаты выполнения обоих заданий.

Т а б л и ц а 1

Распределение всех испытуемых по успешности выполнения задания 1 и задания 2

Мы не можем предполагать нормальность распределения данных, поэтому для проверки значимости различий можно воспользоваться критерием Х2 Ван-дер-Вандена. В данном случае различия в распределении по успешности выполнения задания 1и задания 2 оказались существенны ( р < 0,001).

Таким образом, первая гипотеза подтвердилась: задание 2, действительно, более трудное для учеников, чем задание 1.

Проверка второй гипотезы. Пусть группа 1 - ученики, верно выполнившие задание 1, а группа 2 - ученики, неверно выполнившие задание 1. В табл. 2 представлены данные по успешности выполнения задания 2.

1 Коллектив ВНИКа благодарит школы и Управление образованием ЦАО г.Москвы за помощь в проведении эксперимента.

Т а б л и ц а 2

Распределение групп испытуемых по успешности выполнения задания

Различия в распределении двух групп значимы ( р< 0,001). Процент учеников группы 1, выполнивших задание 2,                  существенно выше, чем процент учеников группы 2,

выполнивших задание 2. Но это подтверждает вторую гипотезу только частично. Ведь некоторые ученики могли верно выполнить задание 2 случайно. Если выяснится, ЧТО все ученики действовали случайно, то результаты по заданию 2 можно аннулировать.

Итак, предположим, что все ученики группы 2 действовали случайно. Но тогда вероятность правильного выполнения задания 2 должна быть равна 25%. Надо проверить, имеются ли                                          существенные различия между теоретическим и эмпирическим распределением.

Т а б л и ц а 3

Распределение испытуемых группы 2 по успешности выполнения задания 2 (теоретическое и эмпирическое)

В данном случае различия в распределении оказались существенны ( р < 0,01). Значит, фактические данные не починяются случайному распределению. Значительная часть испытуемых могла действовать осмысленно и верно выполнила задание.

Предположим, что только 25% учеников действовали осмысленно, тогда они бы дали 75-76 правильных ответов. Если остальные 75% учеников действовали случайно, то было бы еще 55-56 правильных ответов. Тогда возможное количество правильных ответов на задание 2 было бы равно примерно 75 + 56 =131. Это ненамного отличается от фактических данных. Значит, хотя бы 25% учеников, не выполнивших задание 1, осмысленно выполнили более трудное задание 2.

Но ведь могли и в группе 1 некоторые ученики действовать случайно! Для того, чтобы был фактически получившийся процент успешных ответов (52,6%), достаточно, чтобы только 38-40% учеников действовали осмысленно, а остальные 60-62% могли действовать случайно.

Итак, вторая гипотеза не может быть нами принята безоговорочно. Поэтому по данным экспериментальной проверки нет оснований заданию 2 присваивать больший вес, чем заданию 1. Несмотря на заведомо большую предметную сложность, задание 2 не перекрывает все метапредметное содержание задания 1. Обоим заданиям лучше присваивать одинаковый вес. Если ученик выполняет только какое-то одно задание, то он получает 1 балл, если оба - то 2 балла. Тем самым уменьшается влияние случайного выбора решения на конечный результат диагностики.

Выводы

Обычно предполагается, что ученик, обладающий той или иной компетентностью, действует осмысленно при решении соответствующей задачи. При проектировании заданий методик диагностики мы также обычно исходим из предположения, что все ученики действуют сознательно, и успешность выполнения заданий определяется уровнем развития соответствующих компетентностей. Но, как показывают данные экспериментальной проверки наших диагностических заданий закрытого типа, нельзя исключать возможность случайного выбора правильного ответа. Поэтому проблематично присваивать одному какому-то заданию больший вес, чем другому, на основе содержательного анализа этих заданий. Лучше предлагать ученикам большее количество однотипных заданий и тем самым уменьшать влияние случайного выбора правильного ответа на конечный результат диагностики. Это надо учитывать и психологам, и, что особенно важно, учителям новой школы при проектировании методик текущей диагностики метапредметных образовательных результатов [3; 5]. Этот вопрос специально рассматривается в магистерской программе ФГОС ВПО психолого-педагогического образования [6].

Но возможен и другой путь. Можно спроектировать задания так, что их содержание настолько захватит воображение учеников, что они не будут действовать случайно, а будут стремиться действовать содержательно. Тогда предположение о возможности случайного выбора правильного ответа можно будет снять. Такой путь потребует проведения иного типа эксперимента и другой конструкции диагностических методик.