Evolutionary algorithms to generate prompts and verify responses of intelligent assistants

Introduction

Currently, the number of users of intelligent assistants (now commonly referred to as «artificial intelligence» or AI, or «neural networks») is growing exponentially. A significant portion of these users, having neither mathematical training nor programming experience, declare themselves to be advanced AI specialists. This creates problems due to attempts to misuse available intelligent tools, questionable interpretation and practical application of the results obtained, as well as misleading, grandiose statements without real content.

This makes it important to create user support tools for working with intelligent assistants (IA), and first and foremost, it is important to develop tools for automating the work of prompt engineers who prepare prompts for IA.

In general, the result of a subject's interaction with an IA is determined by two factors:

• the semantic content of prompts or other texts presented to the IA;

• the intellectual capabilities of the IA itself, which can vary widely. 

The uncertainty of interpreting the semantic content of prompts or other relevant texts, as well as the known unpredictability of the AI's response to prompts, complicate the application of formalization, requiring its significant adaptation to the new context of application. This work is one of the first attempts at such adaptation. A special notation has been developed to ensure a compact description of the algorithms used.

The generation of plausible but incorrect information, known as «hallucination», remains a problem accompanying the practical use of AI. In particular, it is well known that AI can justify mutually contradictory statements if it receives a corresponding prompt. The only exceptions are strictly substantiated or obvious observable facts. Therefore, it is becoming urgent to find tools that can objectively evaluate the correctness of formulations calculated using AI.

The issues discussed in this paper have become particularly relevant after 2020 (Nikolenko et al., 2020), so there are relatively few relevant publications on the automation of AI and the elimination of the problem of «hallucinations». Among the approaches that inspire moderate optimism are dialogical methods, including the «Debate Game» (Irving et al., 2025) and the Chain-of-Verification Method (Shehzaad et al., 2025), which eliminates «hallucinations» by asking AI to reflect on its own answers and self-correct. However, these approaches are not based on a significant formalization and are hopelessly far from useful practical application.

This paper presents algorithms for solving two problems:

• generating prompts for which the annotations (brief descriptions of the answers to the prompt) are closest to the given description (the solution is provided by an evolutionary algorithm for selecting prompts);

• verifying the correctness of the intelligent assistant's answers (the solution is provided by an evolutionary algorithm for verifying the correctness of IA answers, or the «pendulum algorithm»).

The main components of the above algorithms that determine the calculated result are a newly developed quasi-genetic algorithm that ensures the expansion of the set of prompts, and a method of multidimensional metric scaling, a rigorous description of which is rarely found in publications. The quasi-genetic algorithm is constructed by analogy with the well-known genetic algorithm (Emelyanov et al., 2003), used to solve optimization problems and to train neural networks, with crossover and mutation operations replaced by pseudo-crossover and variation operations performed by AI, which are similar in context but fundamentally different in content.

The main principle implemented in the approach to solving problems is that the intelligent assistant performs all substantive operations related to extracting quantitative estimates from the material under study, followed by analysis of these estimates using methods of multidimensional statistical analysis, statistical hypothesis testing techniques, and other mathematical tools.

The tools, which operate based on the algorithms described below, are implemented in software based on the OpenAI API. These tools have been tested in pilot mode with psychological texts, demonstrating convincing results.

The most obvious prospects for practical application of the presented algorithms are in areas where concepts with significant variability in interpretation are used: in psychology, sociology, art history, and other humanities (Shoham et al., 2009; Nikolenko et al., 2020).

This article is intended for programmers who create tools for working with large language models and mathematicians who develop methods for the practical use of artificial intelligence capabilities.

Notation and basic concepts

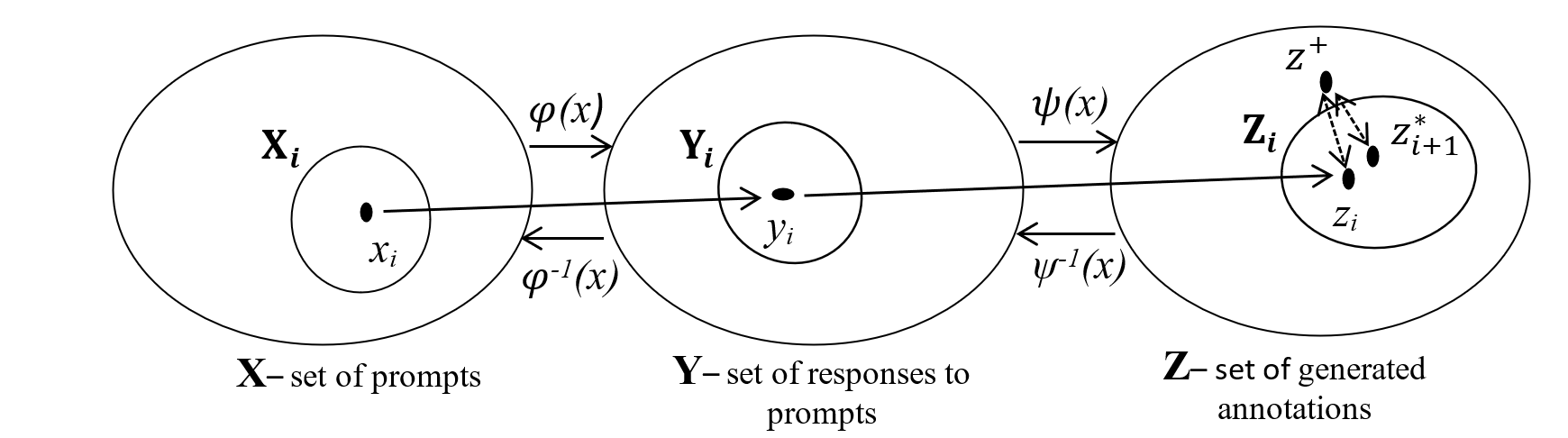
X, Y, and Z are also used as scaling spaces. Distances are understood to be Euclidean distances. Quasi-distances are represented by values from the numerical interval [0;1] and are calculated for given pairs of elements of metric spaces X, Y, and Z using AI as the results of prompts for comparing elements included in given pairs. A value of 1 corresponds to a complete match between the contents of the compared elements, while a value of 0 corresponds to a complete mismatch (obviously, the comparison result is ambiguous and is determined by the characteristics of the AI used). AI prompts explicitly specify the requirement to compare the presented elements, expressing the result as a real number from the interval.

Operations in metric space X:

i++ and j++ — increase the indices i and j by one;

Evolutionary algorithm for prompt selection for AI

The task is formulated as follows.

Solution algorithm:

1. Set a set of basic prompts $X_0$ . $i=0$ . $Y_0={\left\{\phi (x)\right\}}_{{x\in X}_0}=\phi (X_0)$ and $Z_0={\left\{\psi (y)\right\}}_{{y\in Y}_0}=$ $\psi (Y_0)$ for all elements of the sets $X_0$ and $Y_0$ . $z_0^{}=\eta (Z_0)$ .
2. If $i>0$ , then compute the IA-mappings $Y_i={\left\{\phi (x)\right\}}_{{x\in X}_i}=\phi (X_i)$ and $Z_i={\left\{\psi (y)\right\}}_{{y\in Y}_i}=$ $\psi (Y_i)$ for all elements of the sets $X_i$ and $Y_i$ .
3. Find the median of Kemeny $x_i=\eta (X_i)$ and the images of its mappings $y_i=\phi (x_i)$ and $z_i=\psi (y_i)$ .
4. Compute the extension $\omega (Xi)={\mu }_i\left(X_i\right),$ using a quasi-genetic algorithm.
5. Compute the matrices $\chi$ , $\chi$ and $\chi$ .
6. Compute $\vartheta$ , $\vartheta$ , and $\vartheta$ , marking the resulting mutual distances between the elements of the sets $X_i$ , $Y_i$ , and $Z_i$ .
7. Find the Kameni median $\eta$ .
8. Determine the neighborhood of the prompt ${\tau }_{X_i}$ using the mutual distances defined by the matrix $\vartheta$ .
9. Compute IA mappings $Y_i=\phi$ for all elements of the prompt neighborhood ${\tau }_{X_i}$ .
10. Check the condition $(\exists z\in Z_i)(\forall z_i\in Z_i)$ . If the condition is satisfied, then $z_{i+1}^{}=\mathit{arg}\underset{z}{\mathit{min}}$ , delete the specified relative part of the elements $Z_d=$ and their preimages $X_{\mathit{nd}}={\phi }^{-1}(Y_{\mathit{nd}})$ and $Y_{\mathit{nd}}={\psi }^{-1}(Z_i\{Zd)$ and proceed to step 11, otherwise proceed to step 4.
11. Calculate $x_{i+1}^{}={\phi }^{-1}({\psi }^{-1}(z_{i+1}^{}))$ .
12. If ${\rho }_z$ , then $x^{}=x_{i+1}^{}$ and stop, otherwise go to step 13.
13. $X_{i+1}={\tau }_X(x_{i+1}^{})$ .

14. i++.

15. Proceed to step 2.

Quasi-genetic algorithm for performing set expansion of prompts when performing operations  ${\mu }_i\left(G\right)$

1. Set the set of basic prompts $X_0$ . j=0.
2. Check the condition $(\nexists x\in X_j)$ . If the condition is met, go to step 3, otherwise stop.
3. Quasi-genetic selection of elements of the set $X_j$ at iteration j using the «roulette rule» with the distance ${\rho }_z$ as the quality function, where $x\in X_j$ .
4. Formation of the complement $\gamma (X_j)$ to the set $X_j$ by applying pseudo-crossover operations $U,V$ and $N$ , as well as pseudo-mutation $\delta$ , to the elements of the set $X_j$ .
5. Combining the set of prompts $X_j$ corresponding to iteration j and the complement $\gamma (X_j)$ : ${\omega (Xj)=X}_j\cup$ $\gamma (X_j)$ .

6. j++.

7. Go to step 2.

The convergence of the computational procedure is determined by the condition specified in step 10 of its description, the result of which, in turn, depends on the semantic content of the prompts submitted by the AI and the intellectual capabilities of the AI itself.

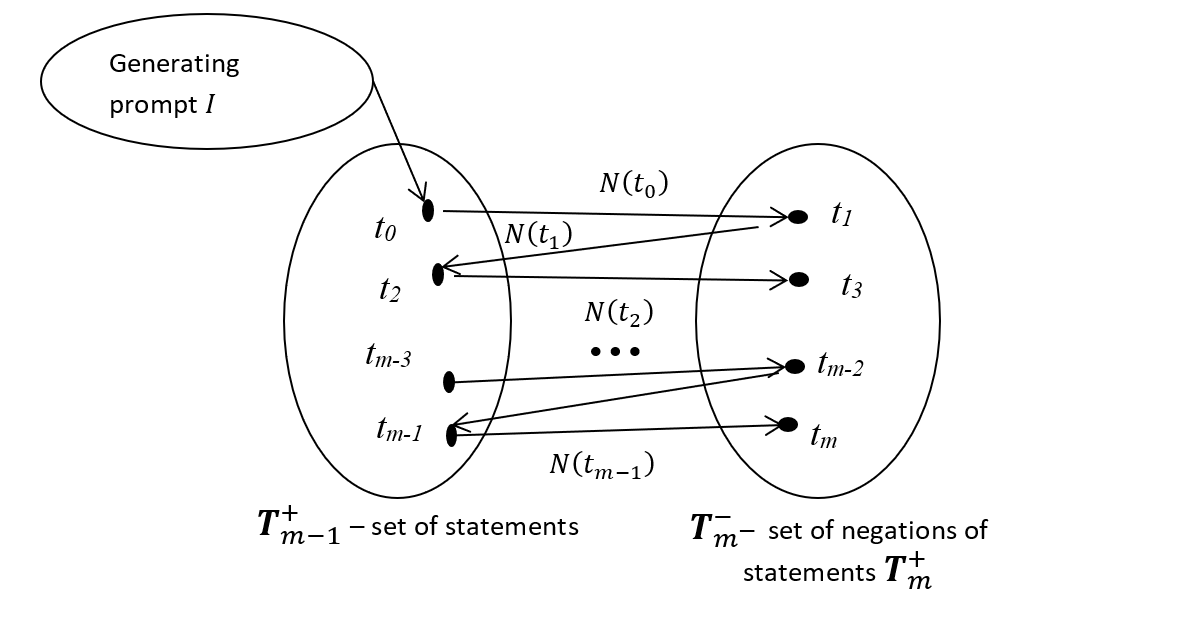
Evolutionary algorithm for checking the correctness of AI responses

Main thesis: AI responses that are correct in content are significantly more consistent with each other than responses that are incorrect in content.

1. Obtain the content material necessary for analysis $t_0$ in response to the generating request $I$ or ask $t_0$ directly. i=0. $T_0^{+=t_0}$ . $T_0^{-=\varnothing }$ .

2. i++.

3. Calculate $t_i=N(t_{i-1})$ .
4. If i is even, then $T_i^{+=T_{i-2}^{+\cup t_i}}$ and $T_i^{-=T_{i-1}^{-}}$ , otherwise $T_i^{-=T_{i-2}^{-\cup t_i}}$ and $T_i^{+=T_{i-1}^{+}}$ .
5. Calculate $\vartheta$ .
6. Calculate the variances ${\Omega }^{+=\Omega }$ and ${\Omega }^{-=\Omega }$ .
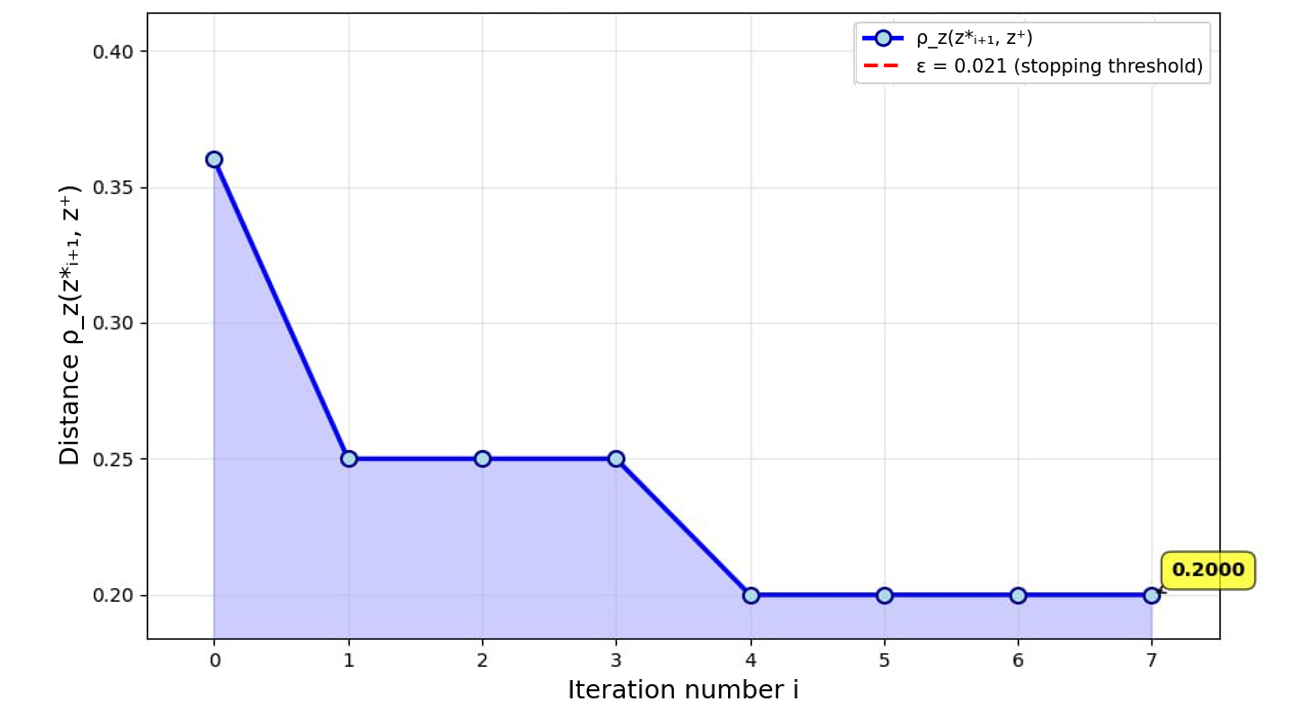
7. Assuming that the distributions of distances to centroids ${\zeta }^{+=\zeta }$ and ${\zeta }^{-=\zeta }$ are normal, test the null hypothesis of equality of variances ${\Omega }^{+}$ and ${\Omega }^{-}$ using the F-test for the statistic ${\Omega }^{-/{\Omega }^{+}}$ if ${\Omega }^{->{\Omega }^{+}}$ , or for the statistic ${\Omega }^{}$ if ${\Omega }^{-<{\Omega }^{+}}$ . If the null hypothesis of the F-test on the equality of variances is not rejected and $i<N_{\mathit{max}}$ , then proceed to step 2, otherwise proceed to step 8.
8. If the null hypothesis of equality of variances is rejected, then if ${\Omega }^{->{\Omega }^{+}}$ , conclude that the content material under investigation is correct $t_0$ , or if ${\Omega }^{-<{\Omega }^{+}}$ , conclude that the content material under investigation is incorrect $t_0$ , otherwise consider the correctness of the specified material to be undetermined.

The convergence of the computational procedure under consideration is determined by the condition specified in step 7 of its description, the result of which, in turn, depends on the semantic content of the prompt generated to the AI (or the original content being studied) and the intellectual capabilities of the AI itself.

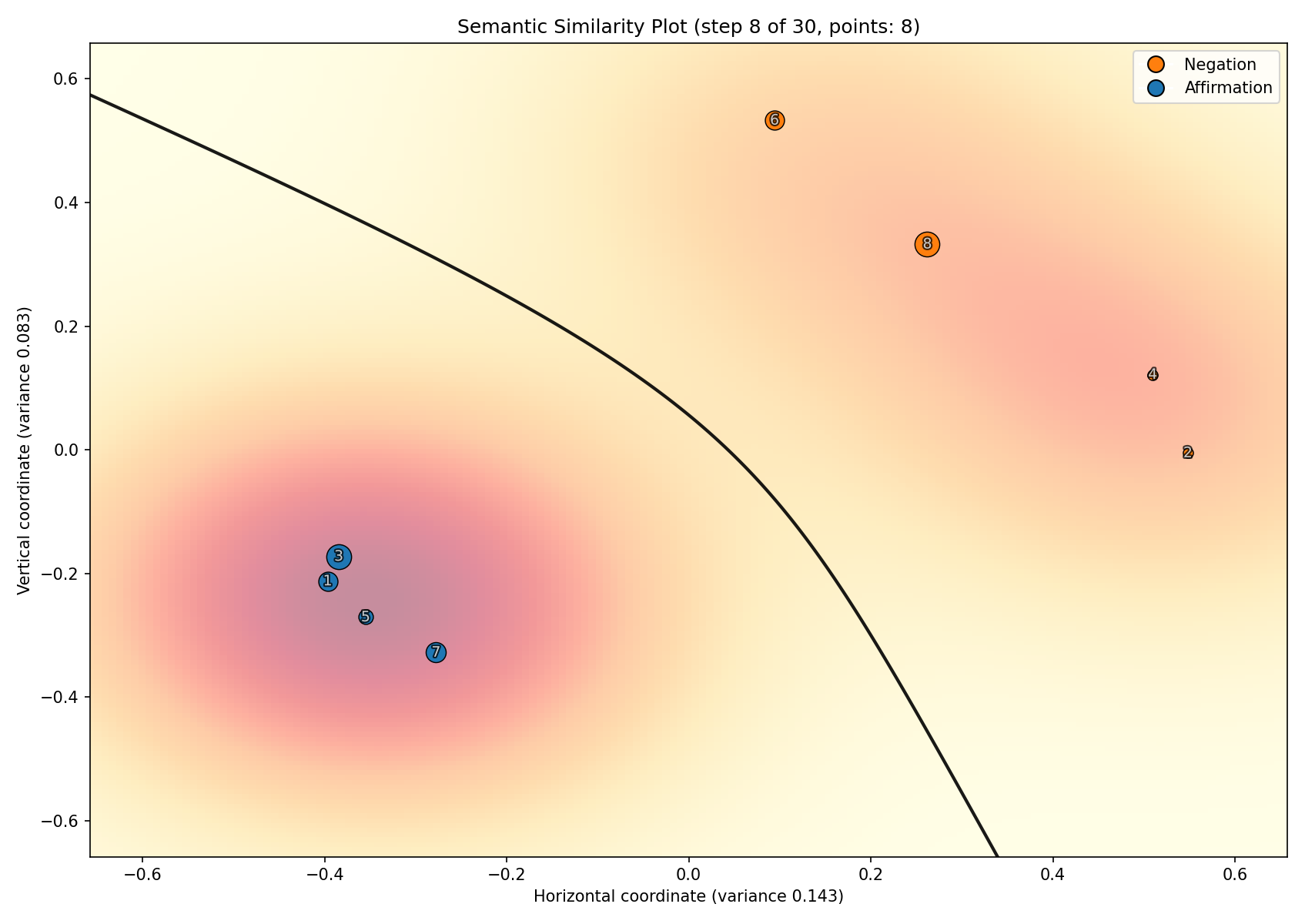
In particular, events can be considered as finding sets of points representing statements and their negations in certain areas of the scaling space or the distribution of certain configurations of points corresponding to the classes of features under study in specified areas of this space (Kuravsky, 2014; Kuravsky, Greshnikov et al., 2024; Kuravsky, Orishchenko et al., 2025; Kuravsky, Yuryev et al., 2024).

Torgerson's multidimensional metric scaling method 

Torgerson's multidimensional metric scaling algorithm

1. Calculate the matrix of quasi-distance squares $D=\Vert d_{\mathit{ij}}={\pi }_{\mathit{ij}}^2\left(m_i,m_j\right)\Vert ,\mathit{где}{m}_j,m_k\in M,i,j=1,\dots ,n\mathrm{.}$
2. Calculate the matrix of mutual scalar products (Gram matrix) $B=\frac{-1}{2}\mathit{JDJ}$ , where $J=I-\frac{1}{n}O{O}^T$ is the double centering matrix, $I$ is the unit matrix of size $nxn,O$ is a column vector of $n$ units, $O^T$ is a row vector of $n$ units (multiplication by the matrix $J$ centers the matrix by subtracting the row mean and column mean from each of its elements and adding the overall mean).
3. Solve the algebraic eigenvalue problem by computing the spectral decomposition $B=E^T\mathit{\Lambda E}$ , where $\Lambda =\mathit{diag}$ ) is a diagonal matrix of eigenvalues in descending order ( ${\lambda }_1\ge {\lambda }_2\ge \dots \ge {\lambda }_n\ge 0$ ), and $E$ is a matrix of corresponding eigenvectors arranged in columns.
4. Compute the coordinate representation $n$ of the elements of the given set $M$ in a linear Euclidean space of dimension $m<n$ by defining the matrix $X={\Lambda }^{1/2}{E}_m$ , where $\Lambda =\mathit{diag}$ ) — diagonal matrix of square roots of $m$ largest eigenvalues of the matrix $B$ , ordered in descending order, $E_m$ — matrix of the first $m$ coordinates of the eigenvectors of the matrix $B$ , arranged in columns (i.e., $m$ first terms of the matrix $E$ ; the coordinates $n$ of the elements of the set $M$ in the matrix $X$ of size $m\times n$ are also arranged in columns).

It should be noted that:

• The Gram matrix $B$ is symmetric and positive semidefinite, which allows it to be represented as $B=X^{T}X$ ; one of the methods for calculating the coordinate matrix $X$ is discussed above;
• It has been proven that the given algorithm provides a solution that ensures the smallest value of the criterion $S$ ;
• The value $S$ is zero when $m=n-1;$
• $Q$ is an orthogonal matrix of size $m\times m$ , and $X$ is a certain k-coordinate solution to the problem that provides the smallest value of the criterion $S$ . Then $QX$ is an equivalent solution that provides the same smallest value of the criterion $S$ .

Results

Generation of a prompt for which the annotation is closest to the given description

The prompts below retain the individual style of wording prepared by an experienced prompt engineer.

• What is the behavioral approach?

• How is behavior studied in psychology?

• What methods are used to analyze behavior?

• What is objective behavior study?

ChatGPT [gpt-4o-mini] was used to solve the problem.

«Create a new prompt combining ideas from the following two prompts.»

«Create a SHORT new prompt, highlighting the common key ideas from the following two prompts. The prompt should be concise (no more than 2-3 sentences).»

«Create a SHORT new prompt, supplementing the first prompt with elements from the second. The prompt should be concise.»

«Rephrase the following prompt BRIEFLY, preserving its meaning.»

«Assess the semantic distance between two texts on a scale from 0.00 to 1.00 as a measure of the difference between their main statements. Be strict: do not underestimate the distance, consider differences in details, level of abstraction, examples, and conclusions. If one text provides a general description and the other provides a specific theory or example, the distance should be increased, even if the topics are similar. Return only one number with two decimal places, without any additional text.»

Verifying the correctness of a thesis using the pendulum algorithm

The prompts below retain the individual style of wording prepared by an experienced prompt engineer.

The phrase «Cultural-historical psychology is based on Marxist theory» was used as the thesis under investigation.

«You are an expert in philosophy, psychology, and scientific methodology. Formulate a clear, well-argued thesis H on a given topic that can be either confirmed or refuted; its plausibility will then be verified by the compactness of clusters of confirming and refuting arguments in the space of meanings. The answer should have a logical structure (thesis, justification, conclusion), be specific and concise (3–5 meaningful sentences).»

Result 1

«Cultural-historical psychology is based on Marxist theory.

Justification: The founder of cultural-historical psychology, Lev Vygotsky uses Marx's ideas about the social context in the development of the individual, emphasizing that psychological processes are formed as a result of social interaction and historical conditions. He emphasizes the role of culture and language in cognitive development, which is consistent with the Marxist concept of the influence of the social environment on the individual.

Conclusion: Thus, it can be argued that cultural-historical psychology is largely based on Marxist ideas, as confirmed by an analysis of the key concepts and principles underlying both approaches.»

«You are working with a chain of theoretical statements.

Formulate a new self-sufficient statement (1–2 sentences) that contradicts the meaning of the given text but remains within the original topic and subject area, preserving the key concepts and changing only the relationships between them.

Do not use metalanguage (such as "argument," "thesis," "this statement/text"), do not paraphrase or quote the original text, and do not offer compromises such as "on the one hand... on the other hand."

Return only the text of the new statement, without explanation.»

Result 2

«Cultural-historical psychology cannot be reduced to Marxist ideas, as its basic principles, developed by Lev Vygotsky, emphasize the uniqueness of cultural factors and individual development, significantly differing from the Marxist emphasis on class struggle and economic conditions.

In fact, the understanding of cognitive development stems directly from the specific cultural context, rather than from Marxist theory about the influence of the social environment.»

The text of request 3 coincides with the text of request 2.

Result 3

«Cultural-historical psychology is closely linked to Marxist ideas, as the emphasis on social conditions and interaction emphasizes that both individual development and cognitive processes cannot be understood without taking into account the economic and social factors described in Marxism. Thus, understanding these processes really depends on analyzing social structures and class relations, the importance of which significantly overlaps the role of unique cultural factors.»

The text of prompt 4 is identical to the text of prompt 2.

Result 4

«Cultural-historical psychology can be understood outside of Marxist theory, as it focuses on unique cultural factors, forms of communication, and linguistic practices that shape cognitive processes independently of economic and social conditions. Thus, individual development and psychology can be studied without relying on class relations or social structures, which highlights the diversity of influences on personality and thinking styles.»

«Estimate the semantic distance between two texts on a scale from 0.00 to 1.00 as a measure of the difference between their main statements. Be strict: do not underestimate the distance, consider differences in details, level of abstraction, examples, and conclusions. If one text provides a general description and the other provides a specific theory or example, the distance should be increased, even if the topics are similar. Return only one number with two decimal places, without any additional text.»

The duration of calculations on a medium-speed computer (processor base frequency — 2.70 GHz) was 71 seconds, with an average duration of 2.34 seconds per prompt to the AI.

Additional observation: narrowing of the chain  $\left\{t_i\right\}$ to the semantic core of the contradiction

1. «Individual experience and unique cultural forms are considered a significant indicator of cognitive development.»

2. «Individual experience is interpreted as a subjective basis, insufficient without analysis of social and structural conditions.»

This observation allows us to consider the pendulum algorithm as a tool that automatically identifies the semantic basis around which a dispute on a given topic takes place.

Conclusion

1. The result of interaction with the IA is determined by two factors: the semantic content of prompts or other texts presented to the IA, and the intellectual capabilities of the IA itself, which can vary widely.

2. The main principle implemented in the applied approach to solving problems is that the intelligent assistant performs all content-related operations associated with extracting quantitative estimates from the material under study, followed by analysis of these estimates using methods of multidimensional statistical analysis, statistical hypothesis testing techniques, and other mathematical tools.

3. An evolutionary algorithm has been developed for generating prompts for the IA, the annotations of which are closest to the given descriptions, as well as an evolutionary algorithm for verifying the correctness of the intelligent assistant's responses.

4. The basis of the evolutionary algorithm for generating prompts is a quasi-genetic algorithm, which ensures the expansion of the set of prompts. The quasi-genetic algorithm is constructed by analogy with the well-known genetic algorithm used to solve optimization problems and, in particular, for training neural networks, with the replacement of crossover and mutation operations with pseudo-crossover and variation operations performed by the IA, which are similar in context of application but fundamentally different in content.

5. The pendulum algorithm allows identifying the semantic basis around which the debate on a given topic takes place.

6. A special notation has been developed to ensure a compact description of evolutionary algorithms.

7. The convergence of the evolutionary algorithm for generating prompts under certain conditions (presented in step 10 of the algorithm description) has been proven, the result of which is determined by the semantic content of the prompts submitted by the AI and the intellectual capabilities of the AI itself.

8. The convergence of the evolutionary algorithm for checking the correctness of answers is determined by the condition specified in step 7 of its description, the result of which depends on the semantic content of the generating prompt to the AI (or the original content material being studied) and the intellectual capabilities of the AI itself.

9. It has been proven that with a sufficiently large number of events, even a single manifestation of a certain pattern actually indicates its existence. Such events can be considered as finding sets of points in certain areas of the scaling space.

10. The pilot application of the developed algorithms for solving psychological problems has demonstrated their effectiveness and semantic correctness.

1. Емельянов В.В., Курейчик В.В., Курейчик В.М. Теория и практика эволюционного моделирования. - М: ФИЗМАТЛИТ, 2003, - 432 с.
   Emelianov V.V., Kureichik V.V., Kureichik V.M. Theory and practice of evolutionary research. - M: FIZMATLIT, 2003, - 432 p.
2. Колмогоров А.Н., Фомин С.В. Элементы теории функций и функционального анализа. – М.: URSS, 2023. -572 с.
   Kolmogorov A.N., Fomin S.V. Elements of the theory of functions and functional analysis. – M.: URSS, 2023. -572 p.
3. Куравский Л.С., Юрьев Г.А., Михайловский М.А., Несимова А.О., Юрьева Н.Е., Поляков Б.Ю. Формирование навыков командной деятельности и их объективная количественная оценка на основе квантовых представлений // Экспериментальная психология. 2024. 17(2). C. 154-177. DOI: https://doi.org/10.17759/exppsy.2024170210.
   Kuravskiy L.S., Yuryev G.A., Mikhailovsky M.A., Nesimova A.O., Yuryeva N.E., Polyakov B.Yu. Formation of teamwork skills and their objective quantitative assessment based on quantum representations // Experimental Psychology. 2024. 17(2). P. 154-177. DOI: https://doi.org/10.17759/exppsy.2024170210.
4. Николенко С.И., Кадурин А.А., Архангельская Е.О. Глубокое обучение.– СПб.: Питер, 2020. – 480 с.
   Nikolenko S.I., Kadurin A.A., Arkhangelskaya E.O. Deep learning. - St. Petersburg: Piter, 2020. - 480 p.
5. Borg and P. J. F. Groenen, Modern Multidimensional Scaling Theory and Applications (Springer, New York, 2005).
6. Cox T.F. and Cox M.A.A., Multidimensional Scaling, 2nd ed. (Chapman and Hall/CRC, Boca Raton, 2001).
7. Cramer H., Mathematical Methods of Statistics. Princeton University Press, 1999. 575 pp.
8. Irving G., Christiano P., Amodei D. AI safety via debate. – Open AI, 2025. 
9. Kuravsky L.S. Quantum Representations and Their Applications in Diagnostics. - М.: Де Либри, 2024. - 128 с.
10. Kuravsky L.S., Greshnikov I.I., Kozyrev A.D., Kosachevsky S.G., Frolova L.I., Zakharcheva A.A. A mathematical model for representing the related operator professional activities and its relevant diagnostic assessment based on the quantum representations, Lobachevskii J. Math., 45 (6), 2534-2551 (2024).
11. Kuravsky L.S., Greshnikov I.I., Orishchenko V. A. Quantum Representation of the Civil Aircraft Pilot Activity. Lobachevskii Journal of Mathematics., 46 (6), pp.2609-2621, 2025.
12. Morrison D. F., Multivariate Statistical Methods, 2nd ed. (McGraw-Hill, New York, 1976).
13. Rao C.R., Linear Statistical Inference and its Applications (Wiley, Hoboken, 1973).
14. Shehzaad Dhuliawala, Mojtaba Komeili, Jing Xu, Raileanu Roberta, Xian Li, Asli Celikyilmaz, Weston Jason. Chain-of-Verification Reduces Hallucination in Large Language Models. - Meta AI, 2025.
15. Shoham Y., Leyton-Brown K. Algorithmic, Game-Theoretic, and Logical Foundations. — London: Cambridge University Press, 2009.