Introduction
The standards for school education emphasize the “use of symbolic means of presenting information to create models of objects and processes of interest, and/or schemes for learning and solving practical tasks” [Federal’nyj gosudarstvennyj obrazovatel’nyj, 2018, p. 6] as one of the most important components of meta-subject educational results.As we apply the Activity approach to educational design, we are to consider model mediation of learning actions as the core of students’ mastering of conceptual thinking.It is through models, that the meaning of a future concept is presented and delivered to students.This defines the quality of forming new actions, which is required for problem-solving [3, 8].Thus, the assessment of students’ capability to work with models within a learning situation, becomes an urgent issue, in particular, the functions of new means of knowledge presentation, which are provided by the teacher.In most cases, students do not refer to any means to organize their own actions and simply manipulate the data from the task without any success.Thus, the adoption of a “conceptual” way of problem-solving by students, is in question — and it brings forth the problem of working with models as the means of one’s own work.Models should not be considered by students as simple “visual” illustrations of the content of the task, to which they should refer only at the teacher’s request, using symbolic means “formally”, and not “meaningfully” [2, 5, 10].
Therefore, the analysis of factors, which determine the effectiveness of the application of modeling means by students, should reflect the indicators of their meaningful use.It is important to choose tasks, which can be solved only if one refers to modeling means.
We have conducted a study to investigate students’ actions with the model, which demonstrates the general way to construct solutions for a problem.22 fourth-grade students of a regular Moscow school participated in the study.The goals of our research were:
— to set up a quasi-learning situation of model acquisition during a lesson.A model should reflect the essential relations within some class of problems;
— to assess the results that students achieve through this kind of instruction;
— to compare students’ performance in these tasks to a number of their meta-subject characteristics, which are related to how students act as they search for solutions to a new problem.
Procedure and results
The experimental one-lesson instruction elaborated the balance scale problem, which is difficult, as both parameters of equilibrium — the weight and the distance of each weight from the fulcrum — have to be considered simultaneously.There are numerous studies [9, 13, 15, 18], which examined the strategies to achieve balance for participants of different age categories, either in the situations of hands-on work with a dynamic model or based on analysis of weights’ configuration drawn on paper.The results of these and other studies [14, 16, 17] convinced us, that the age of our participants (10—11 years) allows them either individually, or with some help from an adult to determine the “rule of balance” in its simplest form and apply it to the tasks of balancing a scale.Most children are familiar with similar situations in their everyday life and know, how they can deal with them (see-saw swing, primitive scale constructions, and others).However, common balancing strategies, which children design as a result of their own search for this problem’s solution, mainly comprise a series of comparisons of “weight” values and “distance from fulcrum” values which also involve the attempts to compensate the lacking or excessive weight with corresponding transpositions [6, 19].The “rule of balance”, which is thus deduced, enables one to solve “simple” problems of equilibrium identification.However, it usually does not provide for grasping the general rule equilibrium assessment in situations with “scattered” weights (when weights are distributed over several suspension points).
Thus, the problems with “scattered” weights were chosen for the quasi-learning situation design.The instruction suggested students master the general way and means to assess the balance of a weights’ configuration, while they were working with a regular school balance scale device.Students were introduced to the matter through a challenging task of balancing three weights, attached to one side of the “scales”, with two weights on the other side, their suggestions were tried out with the real balance scale (Figure 1).
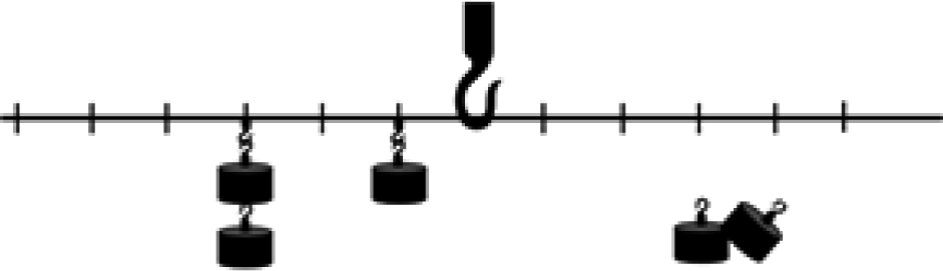
Fig. 1. Balancing unequal amounts of weights on the scale
The procedure for our study was set as a lesson for students, who were to solve a quasi-learning problem.The most common features of a learning situation were reproduced: introducing students to some practical problem; finding out, that the suggested ways to place weights are insufficient; trying out the general way (assessing the “contribution” of each weight to the state of balance) to solve a number of problems and testing the solutions on a dynamic model of the scale; and then — the application of the verified model of equilibrium to solving control tasks.The balance scale problem is not included in the fourth-grade curriculum, and those children, who participated in our study, were not familiar with the way of balancing scattered weights, which was provided during the lesson.The ideas, which students put forward during the introductory problem, confirmed that their placement of the two weights while balancing the other three, was random.
Students were offered a general way to assess (and predict) the balance, which allowed to check any solution: the “load” inflicted by each weight depending on its distance to the fulcrum had to be calculated and the sum of “load” values on each side had to be equal.The rule of modeling the “load” was also explained to children: they were to lay down a “coin” for every “step” that distanced the weight from the fulcrum by one scale mark.This model allowed to assess the present configuration of weights, as well as its possible transformations.The calculations involved (counting “steps” for every weight, laying down “coins” and comparing summary “loads” achieved for each side) were of no difficulty for students.
The training educational tasks, which were provided for students to test the model of equilibrium evaluation (8 tasks: see examples Fig.2, 3) included the following types:
— to estimate the equilibrium for the given weights’ configuration: “Is the scale balanced? Which side outweighs the other?”;
— to restore the balance by adding only one weight unit;
— to suggest several ways to balance an unequal number of weights for both sides of a scale.
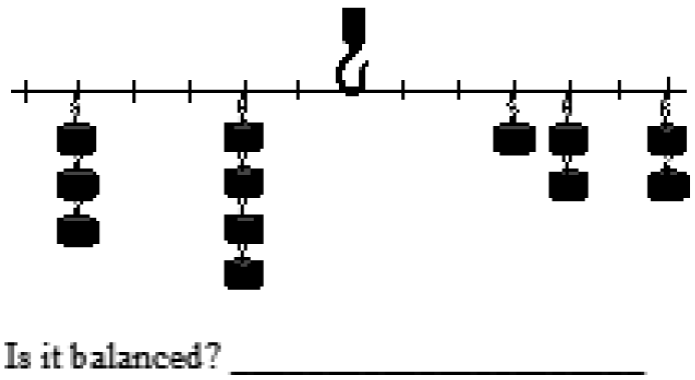
Fig. 2. The estimation of the weights’ configuration
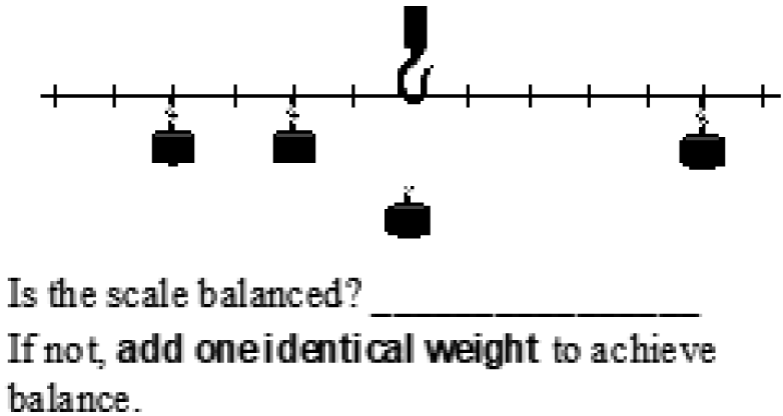
Fig. 3. Balancing the scale by adding one weight
During the lesson the teacher organized the collective work on the problems and oversaw that each participant of the joint problem-solving had the opportunity to check his suggestions on how the weights are to be attached and the coins are to be laid with the actual lever device in front of the class.It was required that each suggestion, which students came up with and discussed, was to be supported with modeling.
At the end of the lesson the students were to accomplish three tasks individually: the tasks were similar to the practice ones, but the hands-on trials were disabled.The students’ performance was evaluated as the number of problems solved correctly.Table 1 presents the students’ results.
The qualitative analysis of the students’ solutions allowed us to split our participants into two groups according to their individual performance (correct and wrong solutions, modeling the “load” as required or ignoring this step):
— I group (10 students): these were the students, who failed in all tasks, or succeeded in only one task, which required to estimate the balance of a ready-made configuration of weights.While solving the control tasks they placed weights in random places and did not refer to the method of “load” calculation, which was provided by the teacher and was tried out in a collective work over training tasks throughout the lesson;
— II group (12 students): those students, who managed to succeed in two or three control tasks.They performed the “load” calculations for each side of the scales: their answer sheets contained drawings of “coins” configurations, which were used for calculations, or the appropriate “load” values were inscribed, which both reflected their reasoning for each problem.
We have additionally conducted the “Transpositions” test, developed by Zak [4, 7], to compare the students’ performance in the experimental quasi-learning situation with the level of cognitive meta-subject results they achieved, which are substantially related to the general approach to solving inquiry-based problems.“Transpositions” assess three components:
— analysis, i.e., search for actions, which determine the subsequent solution’s design;
— reflection, which means the awareness of the general (conceptual) way of solving problems of this kind;
— planning, which determines the accuracy of the operations needed to solve the problem [Ocenka metapredmetnyh kompetencij, 2015, p. 27].
The tasks of this test require rearranging shapes in a given grid in such a way that the location of similar shapes will correspond to the location of similar numbers in the pattern grid, provided alongside.Depending on the difficulty level, the task can be solved in two, three, or four transpositions.All tasks have more than one way to solve them.There are three blocks of tasks.The ability of students to determine the general way to solve the tasks of the first block correctly (where only two transpositions are needed) is the indicator for the students’ reflection.The method, which they extract, can be applied eventually to solving the tasks of the other two blocks (the second block requires three transpositions and indicates the substantial analysis of the tasks’ modifications; the third block requires four operations and assesses the ability to plan a sequence of transpositions).
The students’ performance in the “Transpositions” test are presented in Table 2.
Table 1
The Students’ Performance in Control Tasks
|
Solved correctly |
0 tasks |
1 task |
2 tasks |
3 tasks |
|
Number of students (person) |
4 |
6 |
8 |
4 |
Table 2
The Students’ Performance in the “Transpositions” Test (the average number of the tasks solved, %)
|
Al tasks |
Components |
|||||||
|
Reflection |
Analysis |
Planning |
|
|||||
|
All students |
65,8 |
79,4 |
86,3 |
36,8 |
||||
|
I group |
47,7 |
65,6 |
70,8 |
12,5 |
||||
|
II group |
81,8 |
91,7 |
100,0 |
58,3 |
||||
The significant correlation between the students’ success in balance-scale tasks and in “Transpositions” tasks (Spearman’s rank correlation coefficient rs=0,633, p <0,01) allows us to consider the differences between two groups of students as qualitative, not only quantitative ones.
An additional analysis of the results — defining the approach to problem-solving for each student as either “empirical” (rank=1) or “theoretical” (rank=2) — allows us to describe each group of students by the ways of problem-solving which prevail [11, с. 197—198].The differences in the approach, which the students in the two groups displayed in regard to all three components, are significant according to Mann—Whitney U test (Urefl=20, p <0,01, Uanalysis=12, p <0,01, Uplan=25, p <0,05) — see Fig. 4.
Thus, the majority of students of the first group demonstrated an “empirical” approach to a problem solving, and students of the second group demonstrated a “theoretical” approach, which allowed them to succeed in a sequence of tasks on transpositions using the identified general method.Based on the results of the data comparison, we have pondered over the possible reasons behind the differences in the students’ actions in a quasi-learning situation of mastering the modeling means.
Discussion
The analysis of the data obtained with the “Transpositions” test, allows us to classify the students’ approach to problem-solving as “empirical” (a number of formal procedures aimed to “split” the situation of the problem into separate data pieces), and “theoretical”
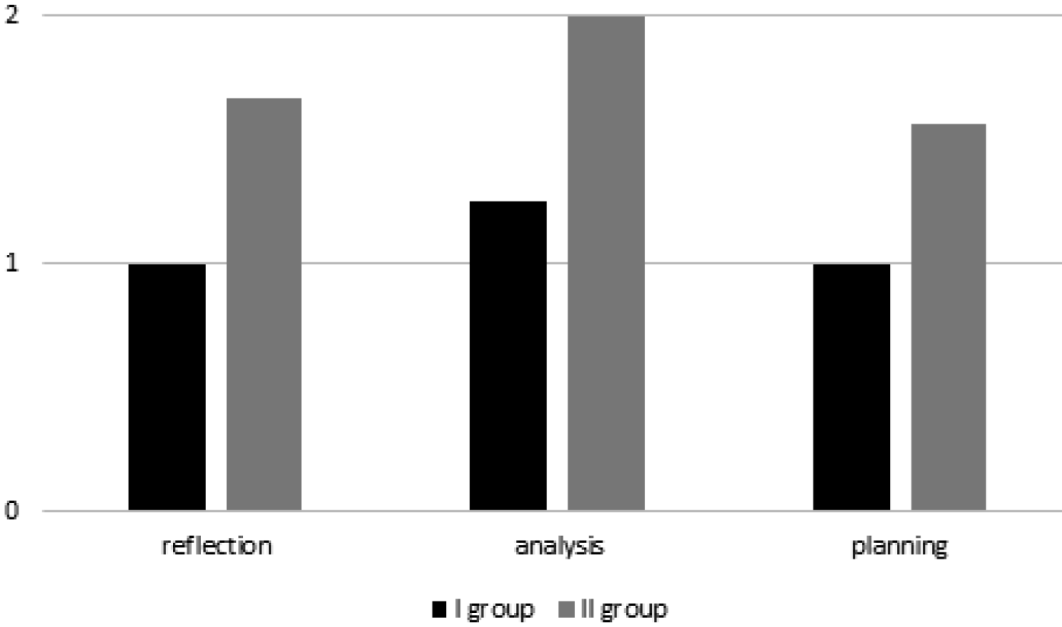
Fig. 4.The distribution of “empirical” and “theoretical” approach to problem-solving in the “Transpositions” test among the students of two groups with different performance in the balance-scale tasks
(substantial analysis of the situation and operations needed to solve the problem).
This classification helps us interpret the differences between the students’ ways of solving the “inquiry-based” task within the quasi-learning situation, which we designed.Judging by the students’ performance in the quasi-learning situation and their level of reflection, analysis and planning, the “empirical” and “theoretical” approaches, diagnosed by the “Transpositions” test, revealed themselves, when students solved balance scale problems using modeling means provided.An obvious, “practical” way of solving these problems usually relies on the consideration of the number of weights and their distance from the fulcrum, rather than on the analysis of the essential terms of balancing the scale.The result of a theoretical calculation of the “load”, caused by all weights on each side, obviously differs from a simple sum of all the weights.To act “conceptually”, each time they moved a weight, students were to lay down “coins” according to the model of the “load”.This method of problem-solving makes the students abandon the usual “trials and errors” method, based on the “eye-catching” parameters of the matter.
Thus, the “empirical” approach may reveal itself in the balance-scale problem solving, as a disregard for the actions, which model the equilibrium with special means.Even though during the lesson, the students have constructed the models for each new task and observed the direct parallel between the calculated “total load” and the equilibrium achieved, in their point of view, these actions may have still seemed “irrelevant”, as some formal accompaniment of a solution.Model building here did not work for them as a means of analysis of the “hidden” relationship between weights and the distance to the fulcrum, which defines the balance, though this analysis makes the relationship tangible and allows students to refer to it in other problems.The “empirical” approach was most likely to prevent some of the students from modeling these implicit relations in their individual work.Students could think, that the “model’s job” was to record the current state of a scale, as required by the teacher, rather than to guide their future actions — and thus, some students managed to solve the simplest task on the estimation of the ready-made configuration of weights, but failed in other control-tasks.Accordingly, these students focused on the partial “rules”, also known as “empirical strategies” [Siegler, 2013], which mostly implied the consideration of the “weight’s” factor and the “distance” factor separately, or sometimes sequentially [6, 9, 17].Within the “scattered” weights condition these “rules” were bound to fail students in their individual work over control-tasks.
The differences of the same kind, most likely, emerge in solving simple problems from the “Transpositions” test, where a general principle was to be extracted and then applied in subsequent tasks.Thus, we consider the characteristics of the students’ performance in the quasi-learning situation, which we have set, as indicative towards the “empirical” or “theoretical” approach in other situations, when some means of conceptual analysis will be provided for the students to master them.
Conclusion
The differences in students’ adoption of the “equilibrium model” as an actual working tool, which were revealed in the quasi-learning situation, were then qualified as indicators of “formal” or “meaningful” attitude towards the preset general way of solving all problems of the kind.During the experimental lesson each balance estimation was done according to the method provided and accompanied with practical trials, nevertheless, almost half of the participants have not even tried to use the model of “balance” in their individual work with control-tasks, and among these students were those, who actively participated in the collective problem-solving.This discrepancy may be, however, understood as we consider the real contradiction of the “visual-active” versus conceptual orientation behind the “hands-on” testing of the ways to achieve balance by moving weights.It is obvious, that the students, who failed in the individual tasks, regarded previous work as some formal “technique” to follow the “real” solution (manipulating weights), rather than a test of the general notion of balance.
The formal acquisition of school information is a common problem in the psychology of education.Bozhovich accurately described “formalism” among students: “These students’ attitude towards school knowledge is characterized by complete indifference to the essence of what they are studying.Often, they treat it as something alien to their life, imposed from the outside, rather than the result of generalization of phenomena and facts of reality”; it is difficult “to put them before a theoretical inquiry-based task” [1, p.308—309].The correct solution of problems, which demand conceptual action (i.e., mediated with the equilibrium model) despite visually presented terms (the opportunity to manipulate weights), may, to our mind, serve as an adequate indicator, that the special “theoretical” functions of the general way to act in such situations were assimilated by students.
The significant correlation between the students’ acceptance of the “equilibrium model” and the “theoretical” and “empirical” level of analysis, reflection and planning, diagnosed independently in similar individual tasks, poses a question about the origins of the related cognitive attitudes, which determine the students’ approach to the means of conceptual analysis of the matter, provided in school education.Will a new task be transformed by a student into a learning task, aimed at mastering the general way of handling the matter, or will it be treated separately, as a particular problem, which demands a “suitable” set of operations? Answering this question, we have to analyze the psychological and pedagogical conditions in which different approaches to the adoption of modeling means, provided by teachers, are formed and developed.The design of diagnostic tasks of a special kind, which allow to assess and predict the effectiveness of students’ promotion within a particular lesson, especially if it includes some opportunities for their personal experiments, is, to our mind, an increasingly urgent challenge for the research.