В сегодняшних образовательных стандартах каждому педагогу предписывается достигать и оценивать метапредметные образовательные результаты. На наш взгляд, метапредметность — это качественная разработанность («добротность», «выделка», «полезность») образовательных результатов, придание им определённой фундаментальной основы с помощью выработанных универсальных учебных действий и ключевых компетенций. Собственно, достигая уровня метапредметности, мы встраиваем личностное знание человека в матрицу современной общечеловеческой культуры. Очевидно, что любой предмет без метапредметной основы «зависает», теряет научные и онтологические корни, свою социокультурную востребованность.
Например, можно дать формальное определение какому-либо понятию или явлению, но можно рассмотреть его в культурно-историческом развитии, диалектических противоречиях, контекстуальных сопряжениях, образно-символических воплощениях, межпредметных и междисциплинарных связях, опытно-практическом применении и т. п. Тем самым формальное понятие превращается в «живое понятие». Добавим, что для метапредметного подхода не бывает малозначительных явлений и процессов. В определённом контексте любая «мелочь» может обрести ключевой смысл (особенно в художественно-образной интерпретации). При этом, конечно, не исключаются особые «узловые точки» или «точки притяжения», которые концентрируют в себе на данный момент особо актуальное содержание.
В этой связи мы не считаем, что необходимо создавать какие- либо специальные метапредметы, как предлагают некоторые учёные (А.В. Хуторской и др.), ведь метапредметы в конечном итоге легко превращаются в очередные предметы. Как представляется, нужно изменить подход к школьным предметам, насыщая их вновь и вновь обновляющимися культурно-историческими, философско-психологическими и научно-методологическими смыслами. И тогда в ходе достижения мета- предметного уровня образования преодолеваются привычные предметные границы, обнаруживаются универсальные смыслы и межпредметные связи, приоткрываются сакральные глубины, казалось бы, ничем не примечательных знаний. Именно свойства открытости и неисчерпаемости позволяют удерживать креативную силу метапредметных достижений для любого поколения педагогов и учащихся.
Приведём пример того, как предметные знания переходят в метапредметные. Возьмём обычную пропорцию. Компетенция, связанная с пропорцией, нужна практически на всех школьных предметах. На уроках математики — это знание обычной и геометрической пропорции, на уроках литературы — это поэтические сравнения, на уроках химии — это расчёт меры смешиваемых веществ, на уроках физкультуры — это чувство равновесия и эстетическое восприятие физической красоты человека, на уроках труда — это способность создать гармоничную и устойчивую конструкцию, на уроках рисования — это использование «формулы красоты» или «золотого сечения», на этических занятиях — это использование «золотой пропорции» в поведении и т. д. Но, самое главное, в результате исследования пропорции до внутреннего мира ученика можно донести то, что она, как уже понимали древние мудрецы (Пифагор, Платон, Аристотель, Плотин и др.), лежит в основе гармонии мира. В последнем случае пропорция приобретает статус универсального знания.
Такая универсальность пропорции говорит о том, что она является своеобразным архетипом общечеловеческой культуры и при определённых условиях способствует становлению общей культуры человека. Можно предположить, что метапредметное содержание проходит сквозной линией через многие учебные предметы, получая на соответствующем материале личностно, социально и культурно значимое воплощение.
Неоценимую помощь в метапредметном освоении материала даёт методологический инструментарий (аппарат), который используется в исследованиях и проектах: проблема, гипотеза, цель, задачи, планирование, методы, приёмы, способы, механизмы, развивающая деятельность, эксперимент, универсальные учебные действия, компетенции, контролирование, рефлексия, прогнозирование т. д.
Действительно, в современном мире невозможно выжить, если человек не обладает такими компетенциями, как предвидение, целеполагание, моделирование, планирование, ориентирование, исследование, контролирование, рефлексирование, прогнозирование, преобразование, которые и составляют основу проектно-исследовательской деятельности. Вот почему в последнее время в образовании особое внимание придаётся именно проектно-исследовательской деятельности.
Как известно, во ФГОСах второго поколения значимое место отводится психологической поддержке образовательного процесса. Можно даже сказать, что стандарты пропитаны психологическими коннотациями. И это не случайно, так как, в конечном счёте, все знания упираются в личность и генерируются личностью. В этой ситуации психолог может занять в современной школе, благодаря своей некоторой «отстранённости» (особому панорамному видению различных формирующих и развивающих процессов), совершенно уникальную и незаменимую позицию, или лучше сказать — статус: он может стать психологом-методологом. Психолог-методолог активно занимается обеспечением проектной и исследовательской деятельности учащихся в урочное и внеурочное время, помогает в этом учителям и, тем самым, продвигает идеи ФГОСов в жизнь.
Слово «методология» обычно пугает практиков, но на самом деле смысл не очень сложный — «установление оснований», «осознание пути», «знание о способах», «постижение метода», «стратегия исследования» и т. п. Методология предполагает процедуру осмысленного отбора центральных положений, ведущих идей, принципов. Таким образом, это система подходов, оснований, методов, принципов, с помощью которых изучается и преобразовывается действительность. Обозначив методологические основания, человек проявляет для себя содержательно-смысловые рамки возможных действий и их последствий. Именно данное слово очень близко проектно-исследовательскому стилю мышления. И кто, как не психолог, в современной школе может достаточно квалифицированно этим заниматься!?
С точки зрения психологии, проектно-исследовательская деятельность обеспечивает особое состояние открытости сознания новому, неизведанному. Проектно-исследовательское сознание, с одной стороны, ориентировано на извлечение знания из опыта, из рефлексии над этим опытом и действиями субъекта в его рамках, с другой — способно порождать на основе знания, полученного опытным путем, некие структурообразующие образы, выполняющие опережающую функцию относительно будущих состояний объектов. Другими словами, проектно-исследовательская деятельность учит жить человека в будущем, в каком-то смысле приближает это будущее и тем самым выполняет превентивные меры.
Сразу оговоримся, что мы сближаем исследовательскую и проектную деятельности, так как они тесно переплетены и в них множество взаимопереходов. Если кратко, то разница заключается в том, что исследовательская деятельность делает акцент на интеллектуальных достижениях (какие мыслительные методы нужно применить, чтобы прийти к данному выводу?), а проектная — на технологических результатах (с помощью каких последовательных опытно-практических процедур может быть получен данный продукт?).
Когда мы знакомимся с ФГОСАми второго поколения, то понимаем, что будущее современного образования в кардинальном сближении мышления педагогов и учащихся: например, педагог создаёт урок-проект и учащийся на уроке моделирует индивидуальный учебный проект. Действительно, педагог должен уметь ставить проблему и учащийся осознанно должен находить противоречие или затруднение, учитель планирует свою деятельность и учащийся составляет план своей работы и т. д. Другими словами, учащиеся выступают полноправными субъектами образовательного процесса. Отсюда ФГОСы создают реальные предпосылки к такому интеллектуальному сотрудничеству. И здесь очень важно достигать данной высокой образовательной планки и удерживать её на соответствующем уровне, для этого требуются постоянные и непрерывные усилия.
Не случайно, что во многих программах развития главной целью является формирование у субъектов образовательного процесса (педагогов и учащихся) компетенций учебно-исследовательской и проектной деятельности как универсального способа освоения и воссоздания действительности (через посредство создания образовательных продуктов), обеспечивающего достижение метапредметных результатов основной образовательной программы основного общего образования (ЗУНы, универсальные учебные действия, предметные умения, общеучебные умения, межпредметные умения, надпредметные умения и т. д.).
Педагог при построении урока оперирует таким понятийным инструментарием, как проблема, гипотеза, цель, задачи, планирование, методы, приёмы, механизмы, развивающая деятельность, ЗУНы, универсальные учебные действия, компетенции, рефлексия, вывод, прогнозирование и т. д. Данные понятия наталкивают на совершенно другое понимание и структурирование образовательного материала. Нужно сказать, что, например, понятие «рефлексия» ещё каких-то десять лет назад в педагогическом общении использовалось крайне редко. А сегодня без него не может обойтись самый элементарный анализ урока или мероприятия.
Если говорить о конкретных проектах на уроках математики, то можно, например, «просто» решать задачи, а можно освоить систему эстетически выразительных и привлекательных задач на заданную тему и оформить их как целостный и самодостаточный проект. Например, подобрать по какому-либо основанию задачи, связанные с равносторонним треугольником (рис. 1).
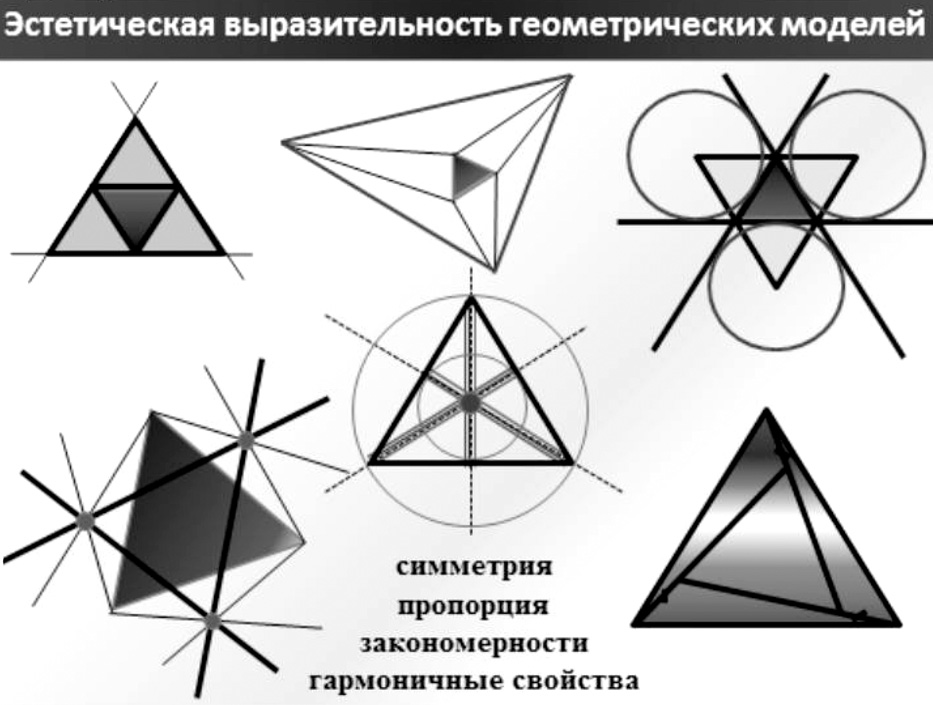
Рис. 1
Можно «просто» решать примеры на заданную тему, но можно подобрать примеры с определённым культурно-историческим подтекстом. Например, русские, китайские, индийские или древнеегипетские задачи на дроби. Очевидно, что в данном проекте могут участвовать большое количество детей: одна группа подбирает задачи из Древней Индии, другая — из Древнего Египта и т. д. Проектным результатом может стать книжечка, а исследовательским — сравнительный анализ задач из различных культур (выявление специфики) (рис. 2).

Рис. 2
Можно «просто» ставить точки на координатной плоскости, но можно моделировать различные эстетически привлекательные фигуры и геометрические формы, параллельно отмечая их гармонию, симметрию или асимметрию (рис. 3).
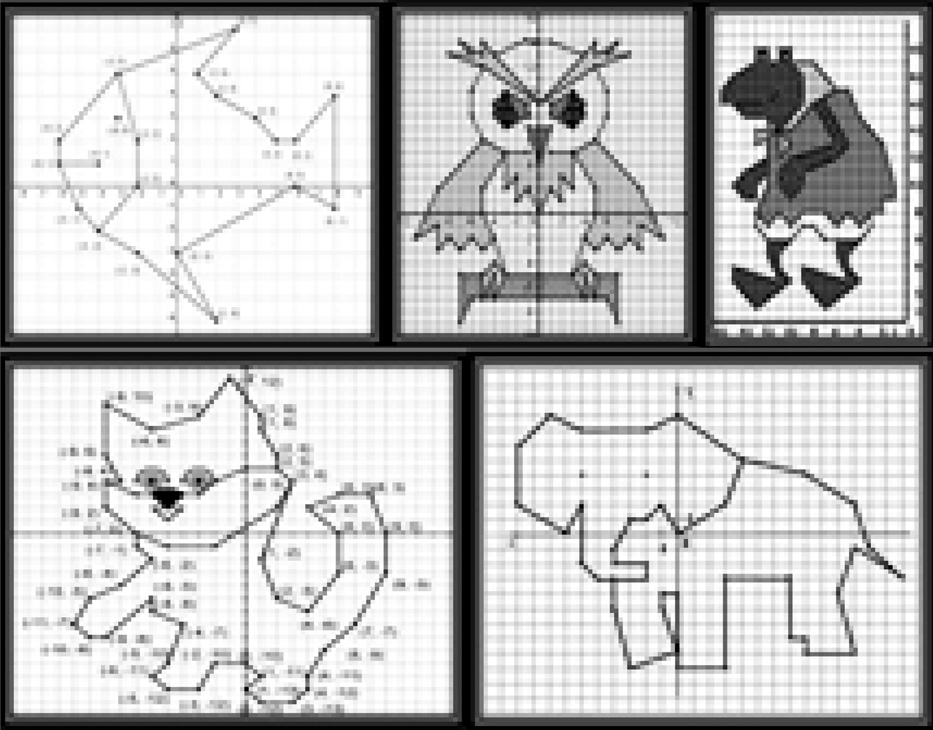
Рис. 3
Можно «просто» весь урок решать задачи на заданную тему, но можно целый урок путём продуманного наращивания, шаг за шагом создавать универсальную образно-геометрическую модель изучаемой темы, которая вберёт в себя прошлые модели уроков (развёрнутые, полные, вертикальные, смежные, внутренние накрест лежащие, внутренние односторонние, соответственные и другие углы) и позволит доказать теорему о сумме углов треугольника относительно любой из трёх вершин (А, В или С). При этом тут же рождается интересная геометрическая задача: используя полученную в ходе урока модель, по одному из известных углов найти величины всех остальных двадцати углов (рис. 4).
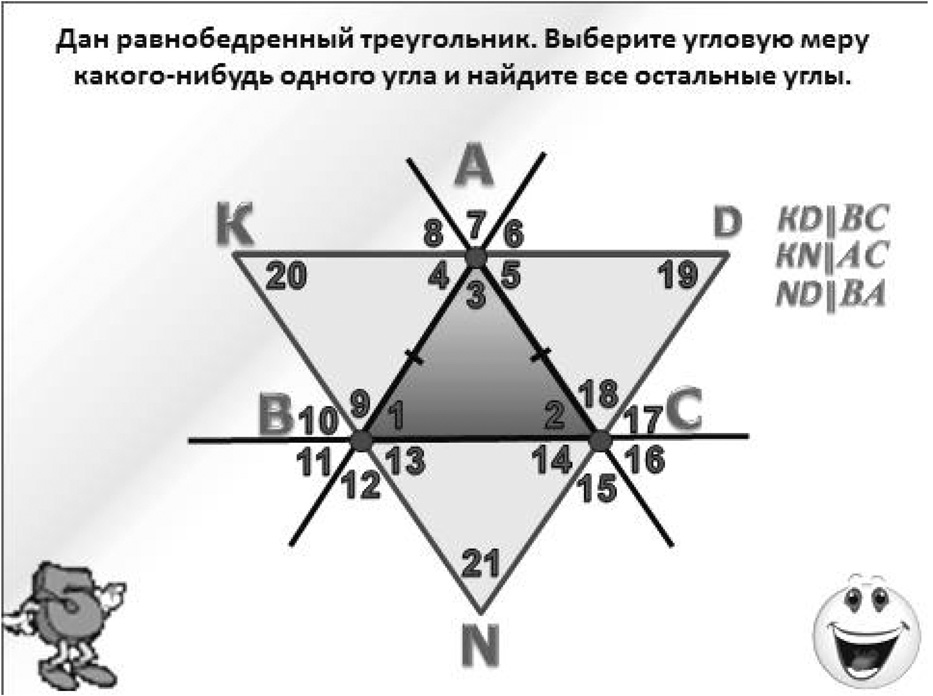
Рис. 4
Поэтому проектно-исследовательский подход трансформирует и углубляет содержание школьного образования, привлекая громадные культурно-исторические и духовно-личностные ресурсы. Другими словами, стоит изменить подход к образовательному материалу и личности ребёнка, как меняется весь уклад школьной жизни, характер взаимоотношений, в том числе такие показатели, как «успешность», «интерес к предмету», «креативность», «коммуникабельность» наполняются новыми смыслами, поскольку проектно-исследовательская форма образовательного процесса кардинально меняет роли и позиции школьника и учителя.
Диагностика и оценка метапредметных результатов проводятся на основании создаваемой субъектами образовательного процесса образовательной продукции — уроков, текстов, моделей, об
разов, исследований, проектов и т. д. Другими словами, учащиеся совместно с педагогами ищут те креативные проектно-исследовательские формы, в которые они могут безболезненно встроиться и выстроить свой образовательный маршрут. В обычном же образовательном процессе педагоги стремятся втиснуть сознание учащихся в уже веками существующие закостенелые учебные формы, чему дети, разумеется, усиленно противятся.
В нижеприведённой таблице (табл. 1) демонстрируются основные этапы-критерии создания и оценки образовательного продукта. Все составляющие должны быть актуализированы, интегрированы и соответствовать друг другу. При этом реализация каждого этапа подразумевает наличие определённой выработанной образовательной компетенции.
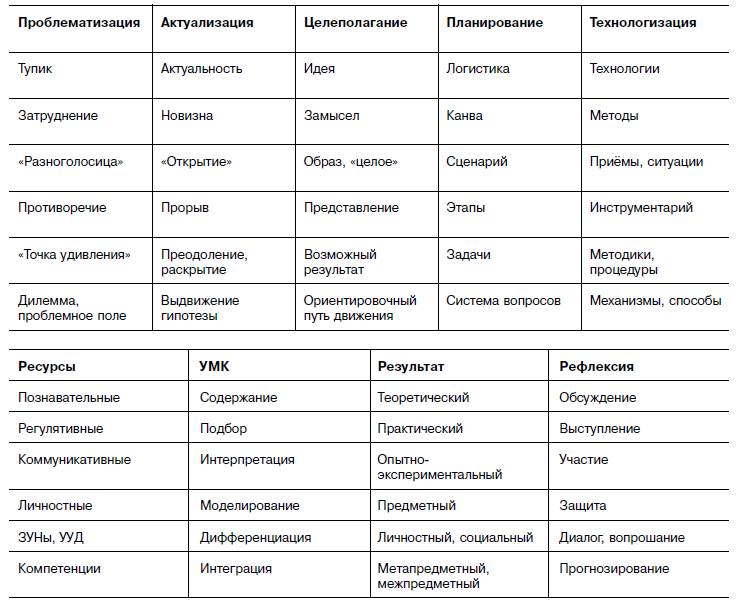
Табл. 1
Собственно, данная таблица и задаёт основные проектно-исследовательские компетенции: постановка проблемы, целеполагание, планирование, прогнозирование и т. д. Наличие данных компетенций у педагогов и учащихся нетрудно проверить в процессе создания, получения и «защиты» образовательного продукта (урока, проекта, исследования и т. д.).
Во внеурочное время образовательное пространство школы — это не нечто дидактико-ангажированное и уроко-подобное, а бытие своеобразных мест («таинственных», «укромных») жизнедеятельности различных сообществ учащихся и педагогов, которые имеют нетривиальные названия, как «Клуб пифагорейцев», «Сообщество алхимиков», «Клуб путешественников», «Поисковая бригада» и т. д. Поэтому различные проекты и исследовательские работы не спускаются сверху, они рождаются и культивируются в гуще жизни различных сообществ педагогов и детей.
Здесь важны следующие условия:
1) проектно-исследовательская деятельность распространяется на всех учителей и учащихся школы;
2) критерии проектно-исследовательской деятельности распространяются на создание всех образовательных продуктов (особый ракурс, подход, взгляд, технология, оценка);
3) в ходе применения проектно-исследовательского мышления (по его стилю) педагог и ученик принципиально не отличаются друг от друга (общие критерии, методы, механизмы), тем самым создаются реальные предпосылки к сотрудничеству.
Развитие каких же метапредметных навыков отслеживает психолог-методолог в различные возрастные периоды?
В начальной школе вырабатываются следующие умения и навыки: обнаруживать и фиксировать изменения в ходе каких-либо процессов, соотносить результат с целью, выявлять признак предмета с помощью сравнения, объединять предметы по общему признаку, различать часть и целое, умение самостоятельно устанавливать последовательность действий и составлять план действий, определять способы контроля и оценки деятельности, предвидеть и настраиваться на трудности, находить и исправлять ошибки в работе, оценивать личностный вклад в общее дело, различать добро и зло.
В основной школе — сравнение и сопоставление объектов по одному или нескольким основаниям; постановка цели, планирование; определение соотношения целей и средств; навыки рефлексии и самоконтроля; навыки самооценки; поиск и устранение причин возникших трудностей; оценивание своих учебных достижений, личностных качеств, своего физического и эмоционального состояния; оценивание своего вклада в решение общих задач коллектива; оценивание своей деятельности с точки зрения нравственных и правовых норм, эстетических ценностей; умение предвидеть возможные последствия своих действий и поступков.
В средней школе — умение самостоятельно и мотивированно организовывать свою познавательную деятельность (от постановки цели до получения и оценки результата); самостоятельный выбор критериев для сравнения, сопоставления, оценки и классификации объекта; элементарные умения прогноза; объективное оценивание своих учебных достижений, поведения, черт своей личности, учёт мнения других людей при оценке, при определении собственной позиции и самооценке; умение соотносить приложенные усилия с полученными результатами своей деятельности; владение навыками организации и участия в коллективной деятельности: постановка общей цели и определение средств её достижения; объективное определение своего вклада в общий результат; оценивание и корректировка своего поведения в окружающей среде; осознание своей национальной, социальной, конфессиональной принадлежности; определение собственного отношения к явлениям современной жизни; осуществление осознанного выбора путей продолжения образования или будущей профессиональной деятельности; выработанная траектория по культурно-нравственному самосовершенствованию.
К серьёзным проектам и исследованиям путь неблизкий, для этого требуется развитие многих универсальных учебных действий и компетенций. Поэтому мы работаем «широким педагогическим фронтом» и не требуем от ребят, чтобы они сразу же создавали полноценные исследования и проекты. И для плавного «наведения» создали следующую таблицу возможных образовательных продуктов, приближающихся к проектам и исследованиям. Ещё раз отметим, что любой образовательный продукт в той или иной мере может отвечать проектно-исследовательским требованиям и критериям, нужно только выработать определённый ракурс и подход (табл. 2).
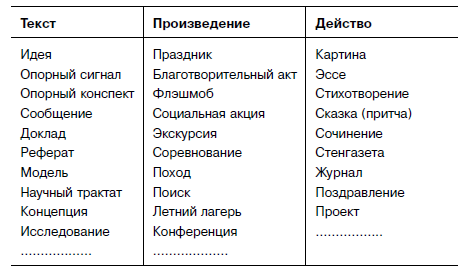
Табл. 2
Значимым фактором по актуализации универсальных компетенций могут стать общешкольные научно-практические конференции, на которых присутствуют педагоги и участвуют учащиеся различных возрастов. Именно на общешкольных конференциях проявляются метапредметные результаты и достижения, которые объединяют педагогов и учеников. Хорошо проведённые конференции заряжают педагогов и ребят творческой энергией, а также рождают новые креативные идеи, которые потом и разрабатываются. И главное — учат масштабному, панорамному или метапредметному видению, мышлению.
Предлагаем вашему вниманию названия и главные идеи конференций, разработанных и проведённых в МОУ СОШ №6 г. Обнинска и других школах России.
1. «Всё есть число» (5-6 классы). Числовое разнообразие в математике выражает смысловое богатство мира. Числовые закономерности позволяют понять явления окружающего мира и раскрыть глубины духовного мира человека. Древние мудрецы пришли к выводу, что вещи суть копии чисел, а числа — начала вещей.
2. «Целое — доля — часть в математике и жизни» (6-7 классы). Между понятиями «целое», «доля» и «часть» существует глубинная взаимосвязь, которую можно найти как в математике, так и в жизни. Целое — это то, относительно чего мы измеряем. Часть — это то, что приобщается к «целому» и тем самым приобретает размерность. Доля — это то, что связывает «часть» и «целое». Пропорция — это гармоническое соотношение «целого», «доли» и «части».
3. «Симметрия в науке, искусстве и жизни» (78 классы). Идея симметрии (асимметрии, диссимметрии) характеризует визуально-пространственное и чувственное равновесие или его отсутствие во внешнем и во внутреннем мире человека и тем самым помогает на эмоционально-физиологическом уровне почувствовать гармонию мира.
4. «Пропорция и гармония мира» (8-9 классы). Различные типы пропорций («обычная», «геометрическая», «золотая» и т. д.) помогают обнаружить разнообразие зависимостей явлений окружающего мира, выразить гармонию мира на языке математики, выявить закономерности духовно-нравственной жизни человека.
5. «Софисты и софистика» (7-9 классы). Софистические доказательства возникают тогда, когда «мерой» всего выступает только человек. Для сохранения объективного взгляда на мир человеку помогают такие структуры, как аксиомы математики, принципы логики, законы мироздания, общечеловеческая культура, абсолютные ценности и т. д.
6. «Истина и логика» (7-9 классы). Для понимания мира и человека очень важно овладеть законами правильного мышления, правилами логики, основами культуры мышления; только тогда человек вправе надеяться на постижение истины.
7. «Великая тайна пифагорейцев» (8-9 классы). Проблема несоизмеримости открыла для человечества новый взгляд на мир, с учётом как его рациональной составляющей, так иррациональной. Гармония и красота мира есть синтез рационального и иррационального.
8. «Парадоксы бесконечности» (9-10 классы). Осваивая различные виды (актуальная, потенциальная и т. д.) математической бесконечности, человек параллельно осваивал и звёздные просторы вселенной, и окружающий мир, и глубины своего внутреннего мира.
9. «Тайны и загадки совершеннейшей формы» (5-11 классы). Совершеннейшая из форм, различные модификации которой выражаются окружностью, кругом, сферой и шаром, благодаря своим удивительным свойствам и признакам, является символом идеальной гармонии и полноты, надёжным ориентиром в человеческих отношениях и переживаниях.
10. «Угловатая форма, устремлённая вверх» (511 классы). Угловатую форму в первую очередь связывают с треугольником и теми фигурами, в которых треугольник является образующим элементом (тетраэдр, пирамида и т. д.). С давних времён с данной формой связывали человеческую устремлённость к идеалам, духовное восхождение. Обнаружить это можно, созерцая великие памятники архитектуры.
11. «Царство многогранников» (6-11 классы). Многогранники, благодаря своим уникальным свойствам, являют нам идеальные модели наиболее компактного, совершенного и гармоничного существования объектов мира. Теория многогранников тесно связана с топологией, теорией графов, линейным программированием и т. д. Недаром многогранник является символом многосторонней одарённости человека.
12. «Этот вероятностный мир» (9-11 классы). Идея вероятности — одна из основополагающих и интригующих идей, лежащих в фундаменте современной науки. Вероятность — количественная мера возможности осуществления события при наличии неопределенности. Вероятностные методы исследований интенсивно входят практически в каждую из наук о природе и обществе. Везде, где наука сталкивается со сложностью, с исследованием сложноорганизованных систем, вероятность приобретает важнейшее значение.
13. «Евклидова и неевклидова геометрии» (911 классы). В 19 веке, благодаря работам Я. Боия, К. Гаусса, Н. Лобачевского и Г. Римана, оказалось, что евклидова геометрия не является единственно возможной. Вслед за ними математики создали и исследовали многие различные «геометрии», которые оказались столь же логичными, стройными и непротиворечивыми. И только в 20 веке учёные доказали, что геометрия Н. Лобачевского нашла применение в специальной теории относительности А. Эйнштейна, а геометрия Г. Римана служит фундаментом для общей теории относительности. Оказалось, что взаимосвязь пространства и времени имеет непосредственное отношение к неевклидовой геометрии. Мир предстал перед человеком не столь «плоским» и «прямолинейным», как в геометрии великого Евклида.
14. «Особенности интегрально-дифференциального понимания мира и человека» (10-11 классы). Для понимания мира человеку приходится постоянно производить операции интегрирования и дифференцирования (в широком смысле). Интегрирование позволяет осмыслить и сохранить полноту мира (удержать его целое), дифференцирование — обнаружить ценность составляющих его частей и мгновений. Взаимообусловленность этих процессов выражается в принципах «всё во всём», «часть подобна целому», «максимум и минимум тождественны», «единое во многом», «различное в одном» и т. д.
Итак, повторим еще раз, что формирование метапредметных результатов учащихся наиболее эффективно осуществлять средствами проектно-исследовательской деятельности, которая опирается на разработанный в последние десятилетия отечественными учёными соответствующий методологический инструментарий. При этом ведущую роль в этом может сыграть школьный психолог, который выступает в роли психолога-методолога и профессионально помогает овладению соответствующими компетенциями педагогам и учащимся.
Версия статьи с цветными иллюстрациями представлена на CD-диске.


Клепиков Валерий Николаевич — кандидат педагогических наук, ведущий научный сотрудник «Института социальной педагогики» РАО, учитель математики МБОУ СОШ №6 г. Обнинска Калужской области.
Беспрозванная Татьяна Владимировна — педагог-психолог, высшая квалификационная категория, МБОУ СОШ №6 г. Обнинска Калужской области.