Введение
Автоматизация психолого-педагогических измерений приобрела широкое распространение с развитием вычислительной техники; очевидным преимуществом компьютерного тестирования перед традиционным является возможность проведения более масштабных выборочных исследований. Параллельно с внедрением компьютеризированных тестовых методик велась активная работа по формированию методологии проектирования тестов с вопросами закрытого типа, был разработан целый ряд концепций (Куравский, 2011; Тюменева, 2007), позволяющих повысить достоверность результатов тестирования, за счет применения оригинальных математических моделей процесса тестирования (Куравский, 2017; Куравский, 2012). До недавнего времени отсутствие подходящей программно-технической базы препятствовало развитию средств автоматизации оценивания ответов на задания открытого типа, с повышением интереса к семантическому анализу ситуация начала меняться. В данной статье изложена концепция параметризации данных, представленных на естественном языке, основанная на использовании современных технологий векторизации текстовой информации и методов нелинейного снижения размерности многомерных данных.
Приводится пример практического применения подхода к текстовым описаниям авиапроисшествий, этот подход легко может быть экстраполирован на задачи обработки ответов, описанных естественным языком на тестовые вопросы открытого типа.
Постановка задачи
Существует выборка наблюдений, характеризующихся набором категориальных переменных и соответствующих им текстов на естественном языке, задача заключается в поиске способа обработки текстовых данных позволяющего автоматически, на основе нового фрагмента текста определить значения соответствующих категориальных переменных, т. е. классифицировать наблюдение. Первичная обработка текстовых данных выполнялась с использованием программного инструмента Word2vecc (Mikolov, 2013), позволяющего получать контекстные вектора слов из векторного пространства, построенного по корпусу текстов при помощи рекуррентной нейронной сети. Параметризованное представление текста, соответствующего наблюдению, вычислялось как среднеарифметическое векторов слов, входящих в этот текст (такой способ представления документа является стандартным (Mikolov, 2013)). Предложенный метод стохастической роевой кластеризации может применяться в комбинации с любой аналогичной, построенной на основе концепции дистрибутивной семантики, технологией параметризации текстовых данных.
Выборку наблюдений обозначим как 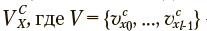 — множество из l наблюдений, характеризуемых классом c и многомерным параметрическим вектором
— множество из l наблюдений, характеризуемых классом c и многомерным параметрическим вектором 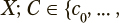
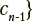 — одно из n возможных значений категориальной переменной;
— одно из n возможных значений категориальной переменной; 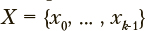 — параметрический вектор из k вещественных компонент (в контексте рассматриваемой задачи — результат параметризации текста). Необходимо определить множество компонент из
— параметрический вектор из k вещественных компонент (в контексте рассматриваемой задачи — результат параметризации текста). Необходимо определить множество компонент из 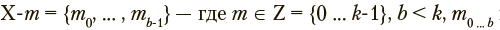 из m уникальны, такое что
из m уникальны, такое что 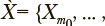
![]() обеспечивает квазиоптимальные значения функционала качества
обеспечивает квазиоптимальные значения функционала качества 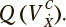
Концепция функционала качества найденного признакового пространства
Если задана категориальная переменная, значение которой известно для всех наблюдений обучающей выборки, для любого результата кластеризации может быть задан функционал качества, связанный с «чистотой» найденных классов в контексте этой категориальной переменной. Тогда поиск подмножества компонент, оптимальных для дискриминации заданных классов, можно считать комбинаторной задачей на поиск одной из 2N (где N — размерность исходного пространства признаков) комбинаций параметров, обеспечивающей наилучшие значения заданного функционала качества ![]() , большие значения которого будут соответствовать результатам кластеризации с большей однородностью кластеров. В качестве метода кластеризации использовался метод k-средних с инициализацией центройдов случайными значениями либо самоорганизующиеся карты Кохонена (Куравский, 2012).
, большие значения которого будут соответствовать результатам кластеризации с большей однородностью кластеров. В качестве метода кластеризации использовался метод k-средних с инициализацией центройдов случайными значениями либо самоорганизующиеся карты Кохонена (Куравский, 2012).
Для формализации понятия «чистота кластера» определим понятие однородность как обобщенную меру отклонения количества наблюдений заданного класса c e {c0, ... , c}, «выигравших» в каждом кластере от общего числа отнесенных к данному классу наблюдений (далее долевая однородность 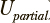 ), и обобщенное отклонение количества уникальных классов наблюдений в каждом кластере от 1 (далее конструктивная однородность
), и обобщенное отклонение количества уникальных классов наблюдений в каждом кластере от 1 (далее конструктивная однородность 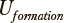 . Если количества наблюдений каждого класса в V сопоставимы, целесообразно дополнить функционал качества характеристикой, отражающей обобщенное отклонение объема результирующих кластеров от ожидаемого объема (например, от среднеарифметического объема l/n), далее для ссылки на этот параметр будет использоваться термин взвешенность W.
. Если количества наблюдений каждого класса в V сопоставимы, целесообразно дополнить функционал качества характеристикой, отражающей обобщенное отклонение объема результирующих кластеров от ожидаемого объема (например, от среднеарифметического объема l/n), далее для ссылки на этот параметр будет использоваться термин взвешенность W.
Графическое представление структурных характеристик результатов кластеризации
В качестве иллюстраций к результатам применения предложенного алгоритма далее будет использоваться графическое представление чистоты кластерной структуры, предложенное исследователем Narayana Swamy (Swamy, 2016). Поскольку такая форма представления (рис. 1) не является стандартизованной, далее даются краткие пояснения по ее интерпретации.
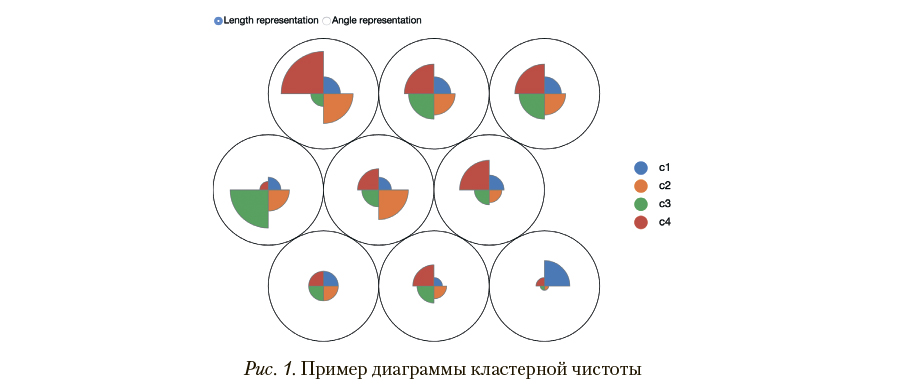
Предполагается, что заранее известны метки классов, кластеризованных наблюдений, их значения перечислены в легенде в правой части рис. 1. Каждому из классов сопоставлен цветовой код, также отраженный в легенде. В основной части диаграммы размещается набор концентрических окружностей, их число соответствует числу кластеров, полученных при выполнении процедуры кластеризации (9 для примера на рис. 1). Отношение площадей внутренних окружностей друг к другу соответствует отношению объемов соответствующих кластеров. Размер секторов во внутренних окружностях соответствует объему наблюдений класса с соответствующей цветовой кодировкой в соответствующем кластере; например, в кластере, представленном левой верхней окружностью, большая часть наблюдений отнесена к классу c4, имеющему красный цветовой код.
Практические оценки функционала качества
Могут быть даны формальные оценки каждой из компонент ![]() , перечисленных ранее. Перед началом вычислений следует получить результат кластеризации
, перечисленных ранее. Перед началом вычислений следует получить результат кластеризации ![]() V^ методом k-средних; множество из j результирующих кластеров далее будет обозначено как
V^ методом k-средних; множество из j результирующих кластеров далее будет обозначено как 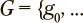
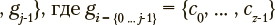 — множество из z меток классов, соответствующих наблюдениям, отнесенным к данному кластеру. Пусть
— множество из z меток классов, соответствующих наблюдениям, отнесенным к данному кластеру. Пусть 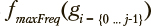 — функция, возвращающая абсолютное количество меток класса, имеющих максимальную долю в i-ом кластере. Тогда долевая однородность может быть оценена как
— функция, возвращающая абсолютное количество меток класса, имеющих максимальную долю в i-ом кластере. Тогда долевая однородность может быть оценена как
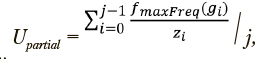
где zi — число наблюдений, отнесенных к кластеру g по итогам кластеризации.
Результат максимизации долевой однородности на выборочных данных при фиксированном числе кластеров отражен на рис. 2
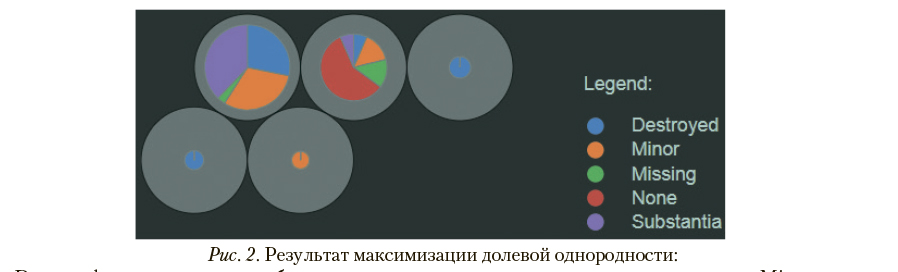
Destroyed — воздушное судно было полностью разрушено в результате происшествия; Minor — воздушное судно получило незначительные повреждения в результате происшествия; Missing — в результате происшествия воздушное судно было полностью утрачено, его судьба не известна; None — воздушное судно не было повреждено в результате происшествия; Substantia — воздушное судно получило значительное повреждения в результате происшествия
Пусть 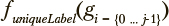 — функция, возвращающая количество уникальных меток класса в i-ом кластере. Тогда конструктивная однородность
— функция, возвращающая количество уникальных меток класса в i-ом кластере. Тогда конструктивная однородность
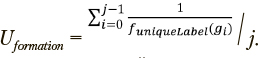
Результат максимизации конструктивной однородности на том же массиве данных отражен на рис. 3.
Несмотря на схожесть результатов максимизации обоих критериев, легко заметить, что в первом случае (рис. 2) предпочтение отдается увеличению доли выигравшего класса в каждом из кластеров, а во втором (рис. 3) меньшему числу классов, представленных в рамках одного кластера.
Оценка взвешенности, основанная на предположении о равных размерах результирующих кластеров,
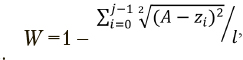
где zi — число наблюдений отнесенных к кластеру gi по итогам кластеризации, l — общий объем выборки.

Destroyed — воздушное судно было полностью разрушено в результате происшествия; Minor — воздушное судно получило незначительные повреждения в результате происшествия; Missing — в результате происшествия воздушное судно было полностью утрачено, его судьба не известна; None — воздушное судно не было повреждено в результате происшествия; Substantia — воздушное судно получило значительное повреждения в результате происшествия
Результат максимизации взвешенности с теми же исходными данными показан на рис. 4.

Destroyed — воздушное судно было полностью разрушено в результате происшествия; Minor — воздушное судно получило незначительные повреждения в результате происшествия; Missing — в результате происшествия воздушное судно было полностью утрачено, его судьба не известна; None — воздушное судно не было повреждено в результате происшествия; Substantia — воздушное судно получило значительное повреждения в результате происшествия
Совокупный функционал качества может быть записан следующим образом:
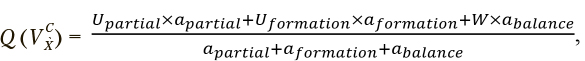
где  — коэффициенты усиления соответствующих компонент заданного функционала качества, позволяющие обозначить желаемые характеристики результатов кластеризации, получаемых в процессе оптимизации. Результат максимизации совокупного функционала качества при попарно равных
— коэффициенты усиления соответствующих компонент заданного функционала качества, позволяющие обозначить желаемые характеристики результатов кластеризации, получаемых в процессе оптимизации. Результат максимизации совокупного функционала качества при попарно равных  отражен на рис. 5.
отражен на рис. 5.
Значения ![]() — нормированы к единице, строгое равенство 1 достигается при описанных процедурах оценки в случае, когда все кластеры имеют равные размеры и внутри каждого из кластеров находятся наблюдения только одного класса.
— нормированы к единице, строгое равенство 1 достигается при описанных процедурах оценки в случае, когда все кластеры имеют равные размеры и внутри каждого из кластеров находятся наблюдения только одного класса.
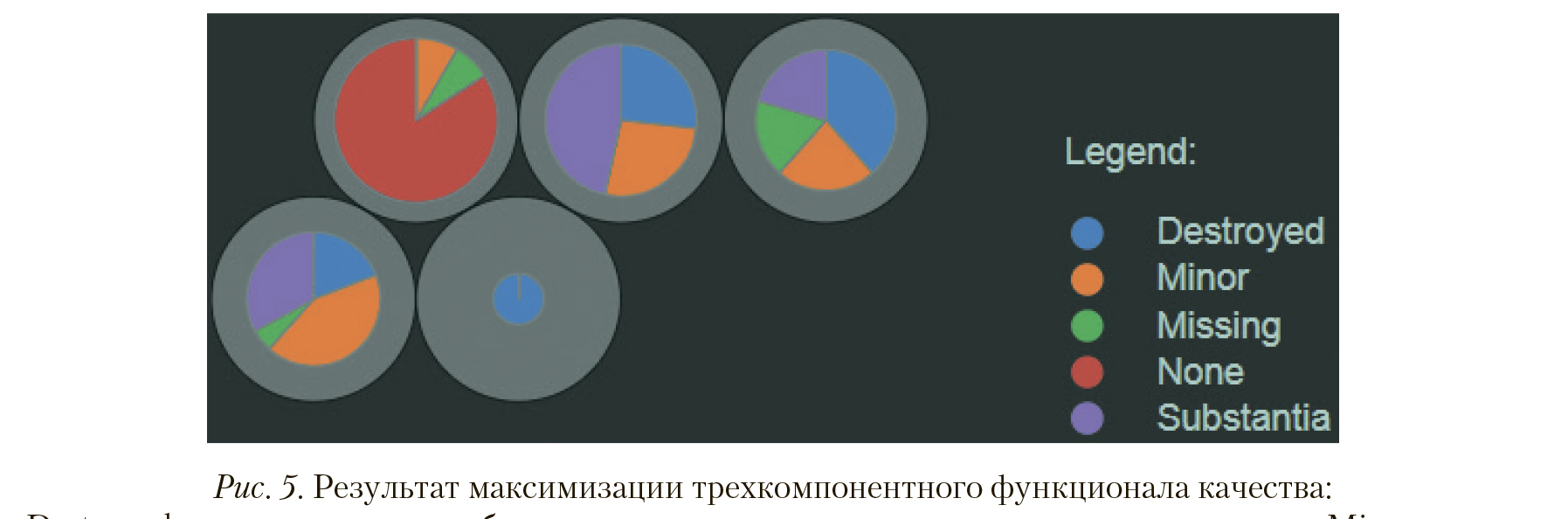
Destroyed — воздушное судно было полностью разрушено в результате происшествия; Minor — воздушное судно получило незначительные повреждения в результате происшествия; Missing — в результате происшествия воздушное судно было полностью утрачено, его судьба не известна; None — воздушное судно не было повреждено в результате происшествия; Substantia — воздушное судно получило значительное повреждения в результате происшествия
Стохастическое решение задачи комбинаторной оптимизации
Как говорилось ранее, задачу поиска ![]() можно рассматривать как задачу комбинаторной оптимизации. Для решения оптимизационных задач, не имеющих явной аналитической интерпретации, часто применяют методы поиска квазиоптимальных параметров, основанные на численных оценках градиента функционала качества, либо на стохастических методах направленного перебора (Гладков, 2009; Куравский, 2017; Формалев, Ревизников, 2004). В этом разделе приводится описание стохастического метода оптимизации, основанного на методе «роя частиц» в приложении к сформулированной проблеме поиска оптимального с точки зрения кластерной чистоты подмножества компонент исходного параметрического вектора, полученного из текстовых данных.
можно рассматривать как задачу комбинаторной оптимизации. Для решения оптимизационных задач, не имеющих явной аналитической интерпретации, часто применяют методы поиска квазиоптимальных параметров, основанные на численных оценках градиента функционала качества, либо на стохастических методах направленного перебора (Гладков, 2009; Куравский, 2017; Формалев, Ревизников, 2004). В этом разделе приводится описание стохастического метода оптимизации, основанного на методе «роя частиц» в приложении к сформулированной проблеме поиска оптимального с точки зрения кластерной чистоты подмножества компонент исходного параметрического вектора, полученного из текстовых данных.
Идея метода «роя частиц» была предложена и развита в работах (3. Kennedy, 1995; 3. Kennedy, 2001; 6. Eberhart, 1995); в оригинальном приложении алгоритм использовался для моделирования социального поведения птиц, пчел и других животных, для которых характерно пространственное перемещение в рамках больших групп (стаи, роя). Позже была отмечена возможность эффективного использования такой модели для исследования признаковых пространств, в частности, поиска квазиоптимальных решений многомерных оптимизационных задач.
Роевые алгоритмы оптимизации можно отнести к эволюционным, общая схема перебора решений описывается следующей последовательностью шагов.
1. Генерируется популяция «особей», каждая из которых содержит некоторое случайное решение целевой задачи. Поиск решения представлен итерационным процессом (п. 2 и 3). В каждой итерации (эпохе) решения (позиции) всех особей незначительно модифицируются по правилам, обеспечивающим схождение итерационного процесса к квазиоптимальным решениям.
2.Вычисляется направление изменения позиции каждой особи, которое зависит от ее текущей позиции, наилучшего решения полученного данной особью за историю ее «существования» (локальным экстремумом) и наилучшим известным решением (полученным любой особью) для всей популяции (глобальным экстремумом).
3. Вычисляются новые позиции особей (их координаты) в соответствии с направлениями, полученными на шаге 2.
4.Проверяются критерии останова; если параметры решения им не соответствуют, переходят к шагу 2, в противном случае поиск прерывается.
Баланс между локальными и глобальными тенденциями в поведении особей определяется коэффициентами интерпретируемыми как ускорения движения особей в направлении локального и глобального экстремума. В первоначальной постановке задачи подразумевалось вещественное пространство решений, что не позволяло использовать метод в задачах линейного программирования, в частности, задачах комбинаторной оптимизации. Рядом авторов была предложена адаптация метода для линейных задач (Eber hait, 1995), при этом «ускорения» получили вероятностную интерпретацию. Рассмотрим более подробно модифицированную версию алгоритма, описанного в (Eberhart, 1995), которая может быть использована для поиска квазиоптимальных в смысле ![]() Q значений
Q значений 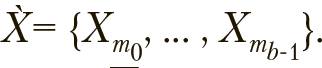 .
.
Поиск оптимальных комбинаций параметров из 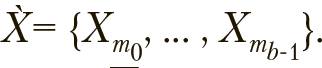 можно сформулировать как задачу о «сборке многомерного рюкзака» с однократным выбором. Ее решение
можно сформулировать как задачу о «сборке многомерного рюкзака» с однократным выбором. Ее решение 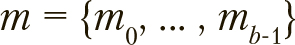 представимо как вектор
представимо как вектор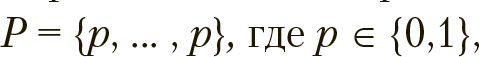 P = {p, ... , p}, его компоненты с номерами из m равны 1, а все остальные 0, т. е. единица в i-й позиции P означает, что хi входит в подмножество компонент
P = {p, ... , p}, его компоненты с номерами из m равны 1, а все остальные 0, т. е. единица в i-й позиции P означает, что хi входит в подмножество компонент ![]() выбранных для кластеризации.
выбранных для кластеризации.
Популяция особей состоит из d решений, каждая из особей хранит текущее решение 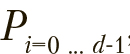 ., лучшее из полученных ей решений
., лучшее из полученных ей решений ![]() . и два вектора
. и два вектора 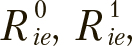 , определяющих частоту инверсии каждого из k бит в каждом из возможных направлений:
, определяющих частоту инверсии каждого из k бит в каждом из возможных направлений: ![]() — вероятность заменить 1 на 0 в позиции
— вероятность заменить 1 на 0 в позиции ![]() для i-ой особи;
для i-ой особи; ![]() — вероятность заменить 0 на 1 в позиции
— вероятность заменить 0 на 1 в позиции ![]() для i-ой особи. Значения
для i-ой особи. Значения ![]() , Rie будут изменяться на каждой итерации, как и позиции особей.
, Rie будут изменяться на каждой итерации, как и позиции особей.
Для позиций каждой особи 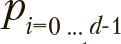 на каждой итерации вероятность инверсии каждого бита
на каждой итерации вероятность инверсии каждого бита 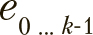 . 1 обозначим
. 1 обозначим 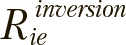 , она будет определяться на основе ее текущей позиции по ... - следующему правилу:
, она будет определяться на основе ее текущей позиции по ... - следующему правилу:
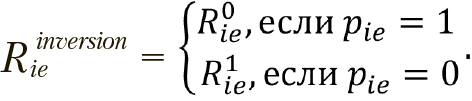 . ..
. ..
На производные ускорения 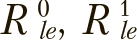 будут влиять их текущие значения, лучшее локальное решение
будут влиять их текущие значения, лучшее локальное решение ![]() , лучшее глобальное решение
, лучшее глобальное решение ![]() и коэффициент инерции
и коэффициент инерции  .
.
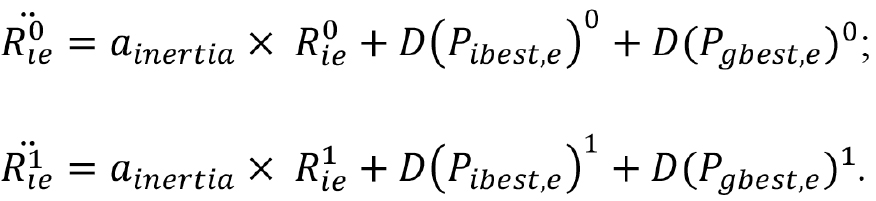
Для вычисления 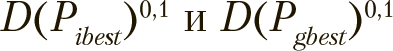 используются два масштабирующих коэффициента
используются два масштабирующих коэффициента 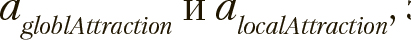 значения которых лежат в пределах {0...1}, они формируют баланс между локальными и глобальными тенденциями в полученной производной позиции. Кроме этого, на каждой итерации рандомизированно генерируется другая пара масштабирующих значений —
значения которых лежат в пределах {0...1}, они формируют баланс между локальными и глобальными тенденциями в полученной производной позиции. Кроме этого, на каждой итерации рандомизированно генерируется другая пара масштабирующих значений — 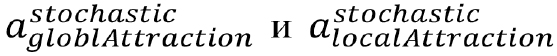 — в пределах {0.1}. Итоговые значения формируются по следующему правилу:
— в пределах {0.1}. Итоговые значения формируются по следующему правилу:
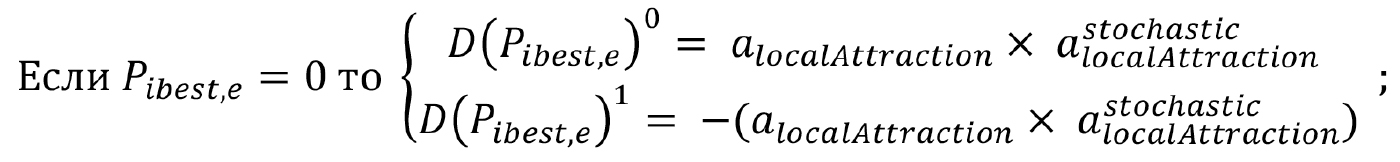
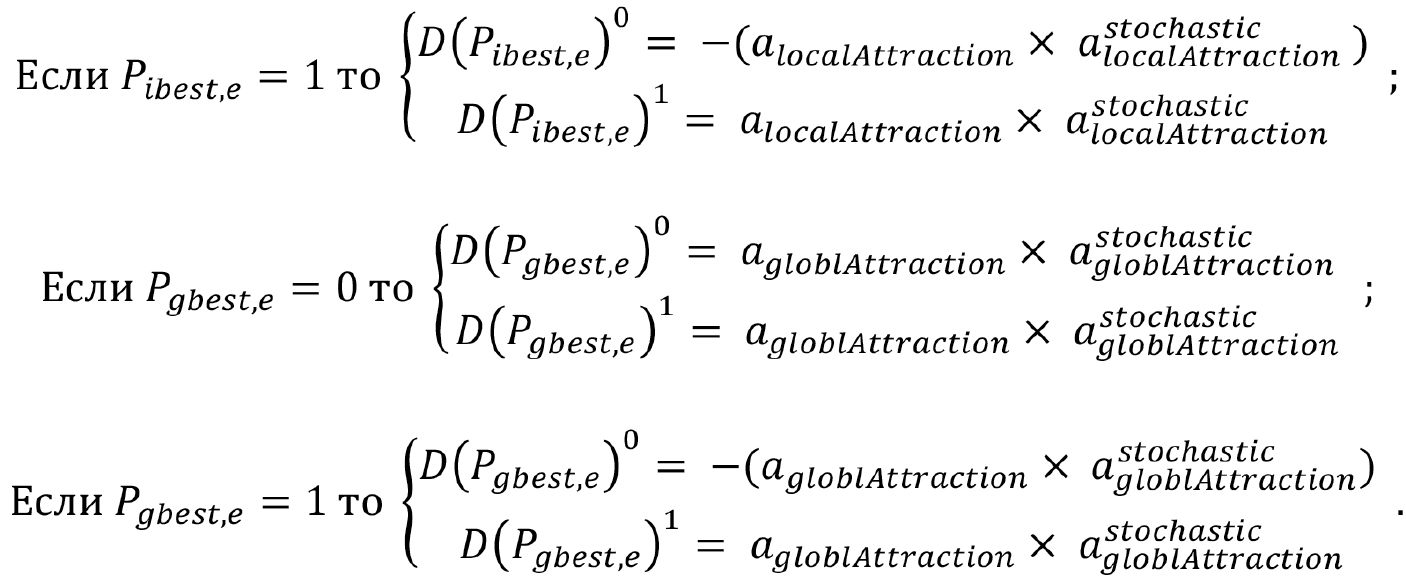
Фактически, вероятность инверсии каждой компоненты вектора снижается при условии, что ее значение совпадает с соответствующим значением известного оптимального решения и возрастает — в противном случае.
Для вычисления новых позиций каждой особи i компоненты соответствующего ей решения e инвертируются с вероятностями 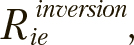 для этого значения
для этого значения 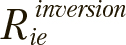 сопоставляются со случайными значениями
сопоставляются со случайными значениями 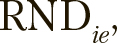 , генерируемыми при каждом сравнении. К вектору предварительно применяется следующее нормализующее условие:
, генерируемыми при каждом сравнении. К вектору предварительно применяется следующее нормализующее условие:
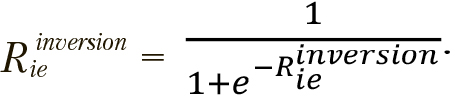
Тогда правило определения производных позиций будет выглядеть так:
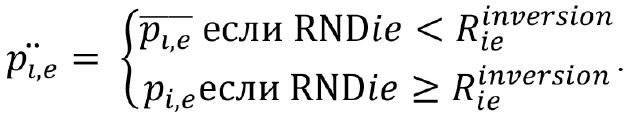
Содержательно приведенный алгоритм соответствует описанному в (Eberhart, 1995). Очевидно, что подобная процедура после определенного числа шагов значительно снизит вероятность появления в популяции новых решений, т. е. алгоритм «застрянет» в точке найденного локального экстремума. Для преодоления проблемы локальных экстремумов предлагается ввести процедуру рандомизации позиций, основанную на критерии «плотности роя». Под плотностью предлагается понимать обобщенную оценку отклонения позиции каждой особи от 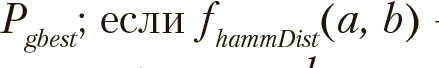 — функция, возвращающая расстояние Хэмминга между бинарными векторами a и b, плотность роя будет оцениваться как
— функция, возвращающая расстояние Хэмминга между бинарными векторами a и b, плотность роя будет оцениваться как
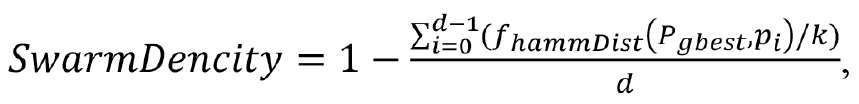 где k —длина бинарного вектора решения, d — количество особей в популяции.
где k —длина бинарного вектора решения, d — количество особей в популяции.
Область значений SwarmDencity соответствует интервалу {0...1}, при этом значение равное единице указывает на то, что текущие позиции всех особей совпадают наилучшим из известных решений, найденных алгоритмом. Значение SwarmDencity оценивается в конце каждой итерации; в случае превышения заданного порога плотности предлагается выполнять рандомизацию позиций определенного процента особей и соответствующих векторов ускорений 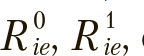 R0e, R1e, с сохранением сведений об их лучших локальных решениях. Такой подход позволяет автоматически выводить численную процедуру из локальных экстремумов без потери общего направления поиска определенного в процессе оптимизации. Мёньшие значения порога для SwarmDencity будут приводить к менее интенсивному поиску решения в области текущего экстремума, и наоборот.
R0e, R1e, с сохранением сведений об их лучших локальных решениях. Такой подход позволяет автоматически выводить численную процедуру из локальных экстремумов без потери общего направления поиска определенного в процессе оптимизации. Мёньшие значения порога для SwarmDencity будут приводить к менее интенсивному поиску решения в области текущего экстремума, и наоборот.
Оценка эффективности при кластеризации данных на естественном языке
Предложенная концепция была протестирована на данных, представленных на естественном языке, об авиапроисшествиях, взятых из открытой базы «Aviation safety network» (Aviation safety network, 2017; https://aviation-safety.net/database/). В исходных данных содержались описания происшествий на английском языке и категориальные переменные, связанные с этим происшествием (уровень повреждений, тип судна, фаза полета и т. д.). Описания происшествий были параметризованны с использованием технологии word2vec и свободно распространяемого словаря, обученного на текстах агрегатора новостной информации Google News;каждому наблюдению был сопоставлен 300-мерный числовой вектор Эти векторы рассматриваются как интегральные оценки семантики описаний, не имеющие явной интерпретации в контексте указанных категориальных переменных. Для проверки предложенного алгоритма был проведен вычислительный эксперимент, целью которого ставилось снижение размерности многомерных векторных описаний с максимизацией их дискриминирующей силы в отношении уровня повреждений, полученных в результате инцидента.
Рассматривались следующие уровни значений повреждения:
• Serious — воздушное судно было существенно повреждено в результате происшествия;
• Minor — воздушное судно получило незначительные повреждения в результате происшествия;
• None — воздушное судно не было повреждено в результате происшествия;
• Missing — в результате происшествия воздушное судно было полностью утрачено, его судьба не известна.
Обучение выполнялось на выборке из 600 наблюдений — 300 использовались в качестве обучающей выборки, 300 — в качестве контрольной. Разделение выполнялось на 4, 8 и 12 кластеров с использованием при вычислении функционала качества метода k-средних и самоорганизующихся карт Кохонена в качестве алгоритмов кластеризации.
Графически результаты этого исследования представлены в табл. 1.
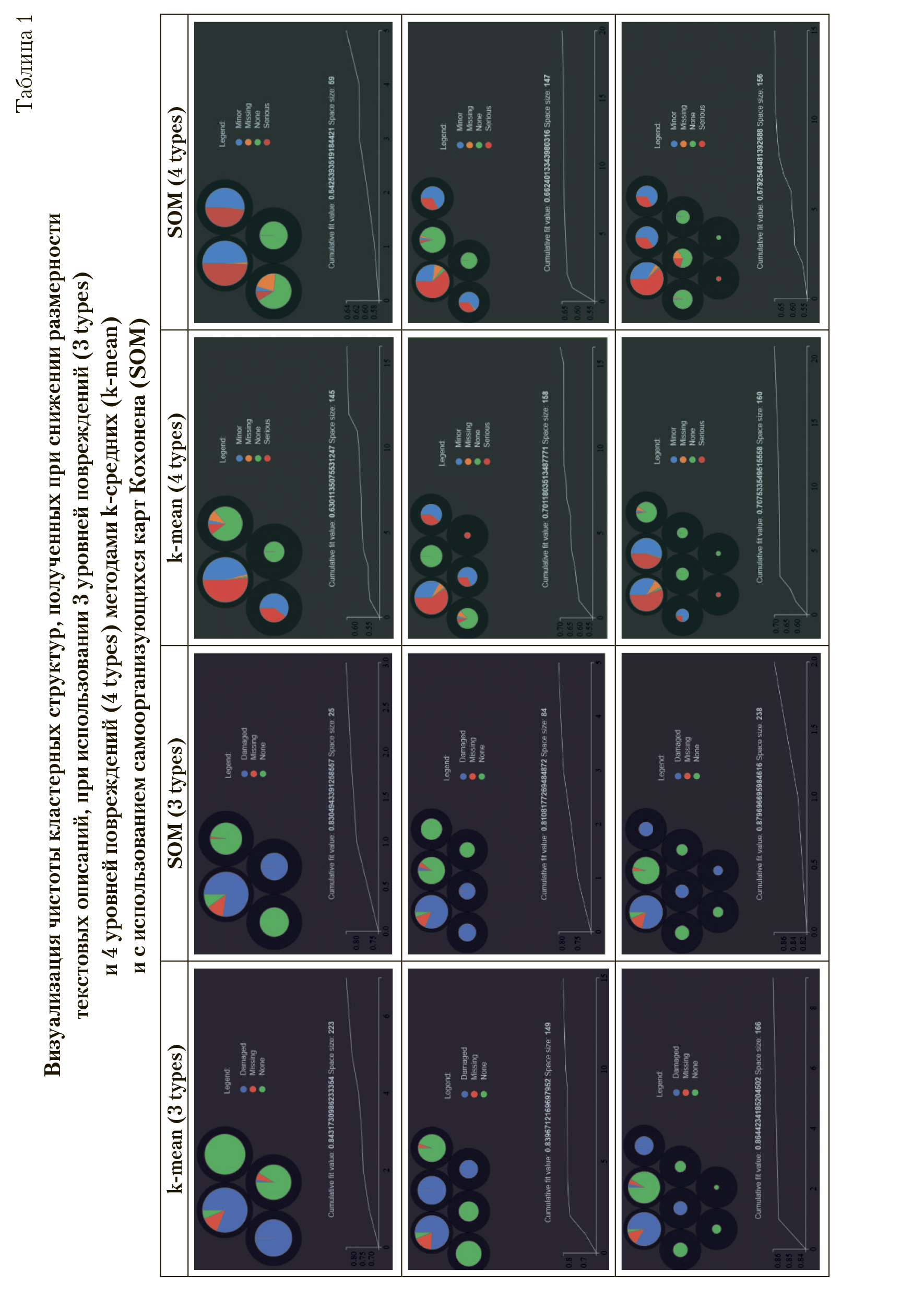
В результатах кластеризации полученных с использованием 4 уровней значений категориальной переменной (уровень повреждения) заметно, что случаи с незначительными повреждениями (minor, синий сектор) и с серьезными повреждениями (serious, красный сектор) регулярно объединяются в один кластер. В действительности, эти описания близки содержательно: использование способа нелинейного снижения размерности для визуализации расположения многомерных (300-компонентных) точек наблюдений в трехмерном пространстве — t-SNE показывает, что точки с соответствующими уровнями повреждений слабо разделимы (рис. 6).

При агрегации категорий Minor и Serious в один класс Damaged (табл. 1, колонки 1 и 2) результат разделения существенно улучшается. В терминах ошибки определения класса на контрольной выборке ошибка составляет ~12% ошибок для разбиения на 4 кластера и ~8% ошибок при разбиении на 6 и 8 кластеров. Результаты слабо зависят от выбранного метода кластеризации. Этот вывод может быть специфичен для данной конкретной задачи.
Визуализация чистоты кластерных структур, полученных при снижении размерности текстовых описаний, при использовании 3 уровней повреждений (3 types) и 4 уровней повреждений (4 types) методами k-средних (k-mean) и с использованием самоорганизующихся карт Кохонена (SOM) CAT — категория событий; NATURE — характер полета; STATUS — статус расследования происшествия; TYPE — производитель и модель, участвующего в аварии воздушного судна; FATE — последствия для самолета, потерпевшего крушение; PHASE — фазы полета. Serious — воздушное судно получило серьезные повреждения в результате происшествия; Minor — воздушное судно получило незначительные повреждения в результате происшествия; None — воздушное судно не было повреждено в результате происшествия; Unknown — уровень повреждения не определен; Missing — в результате происшествия воздушное судно было полностью утрачено, его судьба не известна
Размерность результирующего пространства признаков в каждом из случаев, представленных в табл. 1, составила от трети до одной десятой от исходного числа компонент.
Выводы
Разработан и апробирован новый метод снижения размерности данных, обеспечивающий решения квазиоптимальные с точки зрения дискриминации заданных классов. Метод, в сочетании с технологией параметризации текстов, может использоваться для обработки записей на естественном языке в произвольных прикладных областях.
1. Результатом работы предложенного алгоритма является не только комбинация исходных признаков, но и координаты центров кластеров, объединяющих наблюдения в найденном пространстве (либо обученная сеть Кохонена в случае выбора ее в качестве метода кластеризации).
2. Предложенный метод не требуют предварительных предположений относительно вида исходного распределения наблюдаемых признаков.
3. Было выполнено прототипирование описанной процедуры снижения размерности, подтвердившее ее практическую применимость.
4. Эффективность предложенной технологии оценивалась на примере задач с вещественным исходным пространством. Метод может быть расширен на случай любых исходных пространств, в которых возможно выполнение кластеризации точек методом k-средних.
5. Сформулирован многокомпонентный функционал качества, позволяющий управлять процессом снижения размерности признакового пространства и формировать различные характеристики результирующего пространства.
6. Для комбинаторной оптимизации методом «роя частиц» предложен критерий «застревания» алгоритма в области локального экстремума. Описана процедура вывода алгоритма из этой области, выполняемая по результатам проверки критерия.
Финансирование
Работа выполнена при финансовой поддержке Министерства образования и науки Российской Федерации в рамках Соглашения о предоставлении субсидии от «26» сентября 2017 г. № 14.576.21.0092 (Уникальный идентификатор соглашения RFMEFI57617X0092) на выполнение прикладных научных исследований по теме: «Разработка нейросетевой системы прогнозирования авиапроисшествий и управления рисками безопасности полетов на основе ретроспективных данных, включающих множество параметров и текстовых описаний событий».