Перейти к основному содержанию

Экспериментальная психология
2024. Том 17. № 1. С. 161–180
doi:10.17759/exppsy.2024170111
ISSN: 2072-7593 / 2311-7036 (online)

Математическая модель сопутствующей деятельности пилота и ее применение для объективной оценки его состояния и профессиональной подготовки

3

Куравский Л.С., Козырев А.Д., Грешников И.И.

PDF (RUS)
GS
Информация
в Google Scholar

Аннотация

Представлен новый подход к анализу и диагностике деятельности пилотов, позволяющий сравнивать с точки зрения эффективности применения как различные варианты информационно-управляющего поля кабин экипажей воздушного судна, так и профессиональную подготовку лётного состава. Используемая для этого математическая модель сопутствующей деятельности представляет работу пилота посредством матрицы вероятностей переходов между выполняемыми им операциями. Рассматриваемый подход опирается на свертку прикладных марковских процессов, построенных на базе протоколов деятельности пилотов, в квантовые представления, что позволяет выявлять структуру этих процессов с помощью квантового спектрального анализа. Применение квантовой фильтрации позволяет получать количественные диагностические оценки деятельности пилотов. Приведен анализ результатов экспериментов с участием пилотов различных уровней подготовки, демонстрирующий возможность оценки их профессиональных навыков, а также перспективы применения предложенных методов.

Общая информация

Ключевые слова: комплексная оценка, оценка уровня подготовки экипажа, квантовые представления, квантовая фильтрация, марковские процессы

Рубрика издания: Психология труда и инженерная психология

Тип материала: научная статья

DOI: https://doi.org/10.17759/exppsy.2024170111

Получена: 04.10.2023

Для цитаты: Куравский Л.С., Козырев А.Д., Грешников И.И. Математическая модель сопутствующей деятельности пилота и ее применение для объективной оценки его состояния и профессиональной подготовки // Экспериментальная психология. 2024. Том 17. № 1. С. 161–180. DOI: 10.17759/exppsy.2024170111

Полный текст

Введение

Совершенствование технологий обеспечения безопасности полетов и повышения эффективности управления воздушными судами (ВС) являются в настоящее время одними из наиболее актуальных задач, стоящих перед гражданской авиацией. Их решение невозможно без количественного анализа деятельности пилотов, которые играют в обеспечении безопасности ключевую роль, при этом уровень их профессиональной подготовки является определяющим фактором.

Эффективность управления ВС и безопасность полета напрямую зависят от действий пилотов в сложных и стрессовых ситуациях, их способности принимать быстрые и правильные решения. Оценка деятельности экипажей в различных лётных ситуациях помогает оптимизировать процесс разработки информационно-управляющего поля (ИУП) авиационных кабин и определить наиболее удобный и надежный вариант интерфейса взаимодействия, что требует решения ряда проблем, обусловленных различными психическими и психофизиологическими состояниями пилотов.

Опираясь на накопленный опыт, можно утверждать, что многообразие опасных и нежелательных психических и психофизиологических состояний в полете, а также сложность или невозможность количественных измерений, необходимых для оценки большей части признаков и предикторов этих состояний, делают бесперспективными попытки их одновременного автоматического выявления в режиме реального времени. Учитывая этот вывод, а также то, что практический интерес с точки зрения безопасности полёта представляют не сами эти состояния, а обусловленные ими некорректные действия или поведение экипажа, в работах [1; 3] сделано заключение о том, что диагностику пилотов следует привязывать не к «размытым» по содержанию психологическим понятиям, а к количественно измеримым характеристикам деятельности пилота, выявив на основе эмпирического опыта относительно небольшое количество определяемых экспертами классифицируемых типов недопустимых действий или поведения, представляющих практический интерес.

Такое заключение полностью согласуется с результатами, полученными в рамках так называемого «деятельностного подхода» [6] отечественной школой психологии на основе интерпретации культурно-исторической концепции Л.С. Выготского. Основным принципом этого подхода является «единство сознания и деятельности»: психическое состояние, формируясь в деятельности, в деятельности и проявляется. При этом деятельность не представляет собой набор рефлекторных реакций на внешний стимул, а регулируется сознанием.

Очевидно, что, решая диагностические задачи, следует представлять деятельность посредством количественных (измеримых) показателей. На роль их источников в случае лётного состава могут претендовать данные видеоокулографии, кардио- и пульсометрии, а также электроэнцефалографии.

Принципы построения модели сопутствующей деятельности

Основным критерием для практического использования указанных характеристик является способность различать проблемные и допустимые действия или поведение пилотов с помощью определенных методов анализа данных. В ряде исследований [1; 2; 3; 11—13] демонстрируется возможность создания эффективных диагностических методик, основанных на сопоставлении исследуемых образцов (паттернов) действий или поведения с типовыми паттернами эмпирических данных, накопленными в результате экспериментов. В зависимости от выбора применяемых измеримых характеристик и типа диагностической задачи, в качестве таких паттернов могут использоваться воздействия на ручки управления ВС, параметры состояния ВС, траектории движения взгляда, временные ряды показателей кардио- и пульсометрии, параметры электроэнцефалограмм и т.д.

Подходы, не использующие сравнения с эмпирическими данными, в контексте диагностической задачи не имеют перспективы из-за отсутствия на сегодняшний день достаточно полной и адекватной наблюдениям формализованной модели действий или поведения пилота, опирающейся на выявленные в результате научных исследований количественные психологические и психофизиологические закономерности.

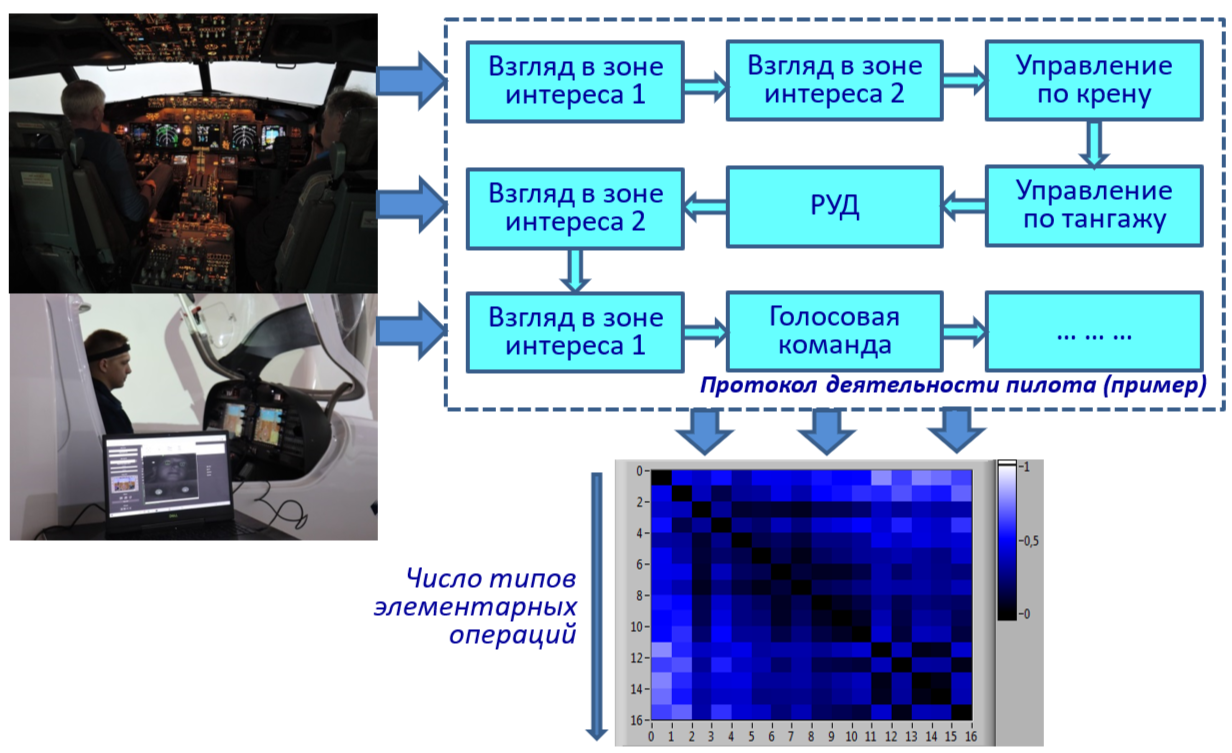
В свою очередь, методы, опирающиеся на сравнение с эмпирическими данными, позволяют формализовать деятельность пилота как последовательность дескрипторов разнотипных элементарных операций, регистрируемых с помощью бортовых измерительных систем. Это может включать в себя:

– попадания взгляда пилота в заданные зоны интереса на приборной доске воздушного судна;

– подачу голосовых команд;

– воздействия на ручки управления;

– смену знака производных по времени от параметров, наиболее значимых при выполнении сложных лётных маневров (а именно: углов атаки, тангажа и крена, перегрузки, приборной скорости, высоты, и т.д. — т.е. тех параметров, которые, как правило, отображаются на командно-пилотажных индикаторах).

В разных практических задачах — в зависимости от объема доступных результатов наблюдений и имеющихся вычислительных ресурсов — могут использоваться различные подмножества показателей из приведенного списка.

Зарегистрированный в результате наблюдений протокол деятельности пилота, представляющий собой последовательность дескрипторов, легко преобразуется в матрицу вероятностей переходов (точнее, в матрицу выборочных оценок вероятностей переходов) между типами выполняемых им элементарных операций, размер которой определяется числом учитываемых типов операций (рис.1). Полученная выборочная оценка матрицы вероятностей переходов, в свою очередь, дает возможность рассматривать динамику действий пилота как марковский процесс с дискретными состояниями и дискретным временем (или марковскую цепь), состояниями которого являются учитываемые в протоколе типы элементарных операций. В общем случае, данный марковский процесс допускает полную систему связей между состояниями. Имеющая место разнотипность операций несущественна, поскольку используются только их вероятностные связи.

Рис. 1. Представление протокола деятельности пилота посредством последовательности дескрипторов элементарных операций и матриц вероятностей переходов

Важно отметить, что во многих прикладных задачах для получения необходимых диагностических заключений достаточно учитывать только сам факт воздействия на ручки управления, не уточняя, в чем они заключались. Информации, заключённой в матрице вероятностей переходов, как правило, вполне достаточно для дискриминации различных состояний и типов поведения пилотов.

Представление деятельности пилотов с помощью матрицы вероятностей переходов между элементарными операциями имеет существенные преимущества перед другими подходами к построению модели их поведения, включая простоту построения представления деятельности по результатам наблюдений, доступность и разумный объем измерений, необходимых для создания модели поведения, и возможность проведения эффективного анализа данных. Распознаваемые типы пилотов определяются прикладной задачей, в интересах которой проводится анализ.

Математическая модель сопутствующей деятельности

Математическая модель сопутствующей деятельности есть формальное представление деятельности пилота посредством матрицы вероятностей переходов между выполняемыми им элементарными операциями. Эта модель предназначена для использования в качестве инструмента для сравнительных оценок эффективности различных технических решений, касающихся построения информационно-управляющего поля (ИУП) кабины экипажа и управления бортовыми системами, по деятельности экипажа, включая сравнительные оценки различных способов построения мультимодального управления ВС и соответствующих им человеко-машинных интерфейсов.

Рассматриваемая модель представляет динамику вероятностей выполнения рассматриваемых типов элементарных операций как марковский процесс с дискретными состояниями и дискретным временем:

p i + 1 = U d p i ,
где значения индекса i ∈ { 1 ,2 , … , N } соответствуют дискретным моментам времени в основной шкале; вероятности выполнения учитываемых типов элементарных операцийв момент времени i представляются как p i = ( p i ,1 , ⋯ , p i , G ) T ; G — число типов элементарных операций (или количество состояний марковского процесса); U d = ‖ u d , ij ‖ — стохастическая матрица вероятностей переходов между типами элементарных операций размера G × G , в которой u d , ij — вероятность перехода от операции j к операции i для исследуемого фрагмента полета d .
Стационарное распределение вероятностей выполнения рассматриваемых типов элементарных операций определяется решением p следующего уравнения:
p = U d p ,
где p является собственным вектором стохастической матрицы U d , соответствующим собственному значению 1 [18].

Таким образом, для выявления уровней подготовки и состояния пилотов на основе протоколов их деятельности используется матрица вероятностей переходов между заданными типами элементарных операций. Эффективность решения прикладной задачи при этом регулируется степенью детализации учитываемых элементарных операций, представляющих и конкретизирующих адаптацию модели к предметной области. Выбор указанной формы математической модели обусловлен высокой эффективностью квантового спектрального анализа матриц вероятностей переходов в сочетании с квантовой фильтрацией при решении задач классификации [9—11].

Альтернативный подход, который опирается на оценки взаимных правдоподобий [1; 7], построенные с использованием матриц вероятностей переходов, при решении данной задачи допустим, однако, как показано в работе [11] и рассмотренном далее примере, этот способ решения существенно уступает по полноте, эффективности и качеству получаемых результатов методу, построенному на основе квантовых представлений.

Математическая модель сопутствующей деятельности обеспечивает сопоставление различных технических решений для одного и того же пилота с выявлением наилучшего варианта. Если, наоборот, зафиксировать техническое решение, касающееся построения ИУП кабины, и сопоставить эффективность деятельности различных пилотов, то данная модель превращается в инструмент для сравнительной оценки уровня их профессиональной подготовки.

Количественная оценка эффективности различных вариантов взаимодействия пилотов с ИУП

Количественная оценка эффективности различных вариантов взаимодействия пилотов с ИУП кабины экипажа и управления бортовыми системами строится на основе сравнений исследуемых вариантов такого взаимодействия с паттернами (эталонами) эмпирических данных, имеющими известную интерпретацию. Указанные сравнения выполняются для матриц вероятностей переходов, представляющих протоколы деятельности пилотов, в спектральной метрике квантовых представлений этих матриц с последующим выполнением квантовой фильтрации. Вид используемых паттернов и структура сравнений определяются прикладной задачей.

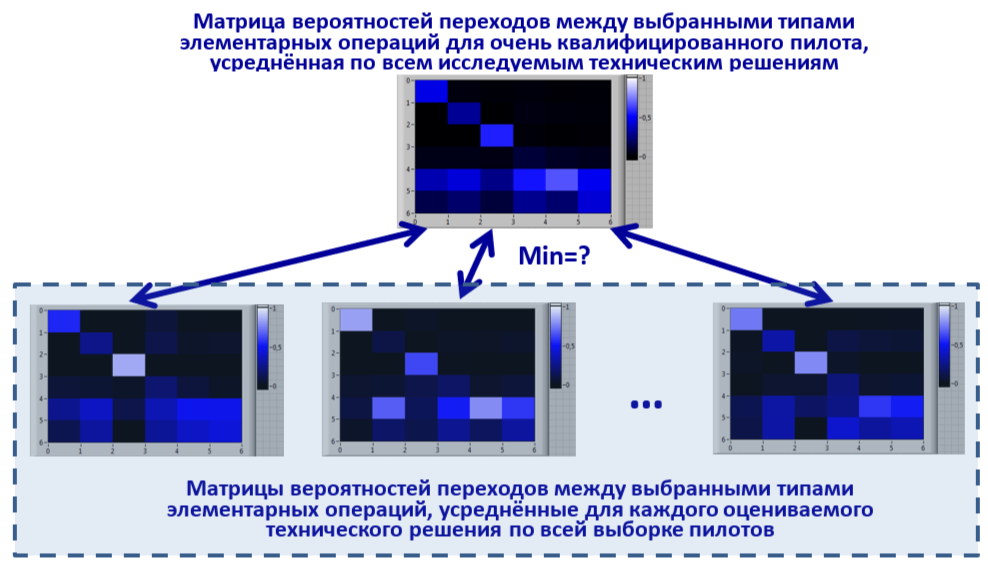
Рис. 2. Схема сравнений при выборе наиболее эффективного варианта ИУП кабины, с использованием математической модели сопутствующей деятельности

Для выбора наиболее эффективного варианта ИУП изменяемой частью сравнений являются различные технические решения по его компоновке (рис. 2). Матрицы вероятностей переходов усредняются по всей выборке пилотов для каждого оцениваемого технического решения. В качестве эталонной используется матрица очень квалифицированного пилота, усредненная по исследуемым техническим решениям (как показали проведенные эксперименты, эта матрица у пилотов с очень высокой квалификацией варьируется слабо). В качестве наилучшего принимается решение с матрицей, ближайшей к эталонной матрице.

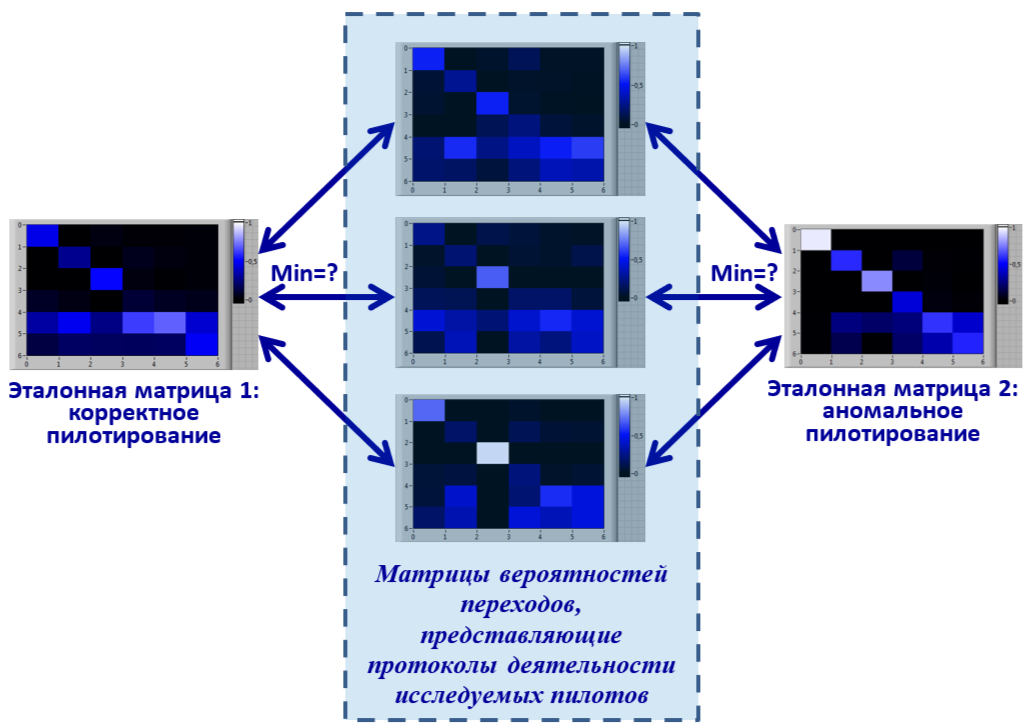
Рис.3. Схема сравнений при оценке эффективности взаимодействия различных пилотов с заданным ИУП кабины, с использованием математической модели сопутствующей деятельности

При оценке эффективности взаимодействия различных пилотов с заданным ИУП изменяемой частью сравнений являются матрицы вероятностей переходов, соответствующие протоколам деятельности исследуемых пилотов (рис.3). В качестве эталонных используются матрицы пилотов с известной интерпретацией (например, представляющие корректное или аномальное пилотирование в различных вариантах). Исследуемому пилоту приписывается оценка взаимодействия, соответствующая ближайшему эталону.

Еще одна полезная схема сравнений рассмотрена далее в рамках примера анализа деятельности пилотов

Построение квантовых представлений марковских процессов

Применимость квантового спектрального анализа [3; 9—11], позволяющего выявлять структуру исследуемых процессов, обеспечивается преобразованием марковских моделей в их квантовые представления. Подобно анализу функций с помощью преобразования Фурье, результаты квантового спектрального анализа выражают внутреннюю структуру случайного наблюдаемого процесса в частотной области. Полученные результаты затем могут применяться для углубленного анализа поведения квантовой системы. Как показывает накопленный эмпирический опыт, данный подход значительно увеличивает объем полезной и значимой информации о поведении исследуемой системы по сравнению с марковскими процессами.

Чтобы представить прикладной марковский процесс данного типа для решения диагностической задачи, используется набор  M кубитов { q k ⟩ } k = 0 M − 1 , размер и величина которого определяются количеством распознаваемых состояний. Полученное представление кубитов отражает переходы между кластерами состояний, число которых значительно меньше числа состояний исходной марковской модели (это обеспечивает понижение размерности задачи). Кластеры распознаваемых состояний определяются на основе эмпирических данных, содержащихся в матрице вероятностей переходов между состояниями марковской модели, преобразуемой посредством процедуры многомерного шкалирования. Кластеризация позволяет выявить информацию, которая является значимой для диагностического решения.

Пребывание марковского процесса в заданном кластере состояний является для рассматриваемых квантовых систем наблюдаемой величиной. «Измеряемые» значения для заданного набора состояний могут быть представлены биполярными константами, например:

  • марковский процесс находится внутри множества заданных состояний: 1,

  • марковский процесс находится вне множества заданных состояний: –1.

Исследуемые марковские процессы могут быть выражены с помощью квантовых представлений пребывания в соответствующих кластерах состояний, а именно: вероятностная структура, представляемая кубитами, описывает динамику пребывания в нескольких кластерах состояний, причем рассматриваемый процесс в любой момент времени находится в одном и только одном из M рассматриваемых кластеров.

Пребывание процесса в кластере состояний k ( k = 0 , … , M − 1 ) представляется кубитом q k ( t ) ⟩ = A k ( t ) ∨ a k ⟩ + B k ( t ) ∨ b k ⟩ , где t — время; a k ⟩ и b k ⟩ образуют базис, элементы которого становятся результатами наблюдений за системой кубитов; A k ( t ) , B k ( t ) ∈ C ( C − множество комплексных чисел ); | A k ( t ) | 2 + | B k ( t ) | 2 = 1 , где | A k ( t ) | 2 согласно правилу Борна рассматривается как вероятность пребывания в кластере состояний 𝑘; | B k ( t ) | 2 согласно тому же правилу рассматривается как вероятность отсутствия в кластере состояний k (т.есть пребывания в любом другом доступном кластере системы j ≠ k , который не совпадает с кластером i ).
Векторы a k ⟩ и b k ⟩ получаются в результате наблюдений за системой кубитов, а именно: каждое такое наблюдение («измерение») дает a k ⟩ или b k ⟩ с двумя очевидными условиями нормализации, следующими из приведенных выше определений A k ( t ) и B k ( t ) :
∑ k = 0 M − 1 | A k ( t ) | 2 = 1 , | B k ( t ) | 2 = ∑ j ≠ k | A j ( t ) | 2 .

Структурная схема, представляющая алгоритмические аспекты данного подхода, представлена на рис. 4.

Рис.4. Структурная схема, представляющая анализ марковских процессов на основе квантовых представлений 

Как отмечено в [9; 10; 16], преобразования нормализации делают представленные кубиты запутанными по измерениям (entangled by measuring — EM). Совокупность таких кубитов далее называется EM-квантовой системой. Нормализация формирует ограничение, накладываемое прикладными задачами. Фактически, рассматриваемые кубиты используются как своего рода «зонды», которые получают информацию о состоянии системы и формируют фон для диагностических выводов.

Каждый кубит q k ( t ) ⟩ рассматривается как формальная квантовая структура, эволюция которой в закрытом режиме описывается некоторым унитарным оператором эволюции U k ( t 0 , t ) k -й квантовой системы:

q k ( t 0 + t ) ⟩ = U k ( t 0 , t ) ∨ q k ( t 0 ) ⟩ ,
где q k ( t 0 ) ⟩ — текущее состояние исследуемой замкнутой системы в момент времени t 0 , q k ( t 0 + t ) ⟩ — последующее состояние той же замкнутой системы в момент времени t 0 + t .
Оператор унитарной эволюции U k ( t 0 , ∆ t ) , который отвечает за эволюцию системы в течение малого промежутка времени ∆t (от q k ( t 0 ) ⟩ в момент времени t 0 до q k ( t 0 + ∆ t ) ⟩ в момент времени t 0 + ∆ t ) можно выразить как I − i ∆ t H k + o ( ∆ t ) , где H k — оператор Гамильтона (гамильтониан) k-й квантовой системы; I — тождественный оператор. Это выражение вытекает из непрерывности оператора U k ( t 0 , ∆ t ) , причем − i ∆ t H k является его главной линейной частью приращения.
Если гамильтониан H k установлен, то полное поведение k-го кубита определяется решением уравнения Шрёдингера, записанного для оператора U k :
d dt U k ( t 0 , t ) = − i H k U k ( t 0 , t ) .

Применяемая вероятностная модель квантовых представлений подтверждена известными физическими экспериментами [16].

Решение уравнения Шрёдингера имеет вид: U k ( t 0 , t ) = U k ( t 0 ,0 ) e − i H k t . Эрмитовы операторы { H k } k = 0 M − 1 определяются биполярными собственными значениями (–1 или 1). Для представления решения уравнения Шрёдингера допустим известный оператор вращения, использованный в работах [9—11] для описания поведения квантовой системы:
U k ( t 0 , t ) = U k ( t 0 ,0 ) ( cos t − sin t sin t cos t ) .
Скорость эволюции различных кубитов может различаться, при этом все кубиты, находящиеся в одной и той же EM-квантовой системе, должны эволюционировать в одном и том же масштабе времени. Поэтому для каждого кубита q k ( t ) ⟩ должен быть определен частотный параметр θ k . Приведенный выше оператор вращения принимает вид:
U k ( t 0 ,0 ) ( cos ( 2 π θ k t ) − sin ( 2 π θ k t ) sin ( 2 π θ k t ) cos ( 2 π θ k t ) ) ,
где t — общее время; θ k — частота вращения кубита. Эволюция, представленная таким образом, выражает скрытую периодичность нахождения в заданных кластерах состояний в течение периода наблюдения.

Идентификация параметров представлений кубитов, выполняемая отдельно для каждого из исследуемых процессов, и сопутствующие проблемы представлены в работах [9—10]. Путем имитационного моделирования динамики марковской цепи в соответствии с вероятностями переходов между состояниями соответствующих матриц генерируются выборки траекторий прохождения кластеров состояний для каждого распознаваемого класса объектов. Эти выборки и выявленные параметры представлений кубитов используются для вычисления элементов матриц взаимных расстояний в определенной далее спектральной метрике.

Для исследуемой ЕМ-квантовой системы в качестве спектра анализируемого процесса рассматриваются значения частот { θ k } k = 0 , … , M − 1 и наблюдаемые числа попаданий { F k } k = 0 , … , M − 1 в кластеры состояний k = 0, …, M − 1 в моменты времени { t j } j = 1 ,2 , … , N , которые называются амплитудами { L k } k = 0 , … , M − 1 . При анализе поведения ЕМ-квантовой системы оцениваются скрытые периодичности попаданий в рассматриваемые кластеры в течение периода наблюдений. Спектральная метрика [9—10] оказалась эффективной для сравнения спектров пар вариантов поведения системы:
w uv = M − Z uv e − β ∑ k = 0 M − 1 ( L u , k − L v , k ) 2 ,
где u и v ( u , v = 1 , … , Z ) — пара индексов сравниваемых Z процессов такого поведения; w uv — расстояние между процессами u и v ; Z uv — количество совпадающих частот { θ u , k } k = 0 , … , M − 1 и { θ v , k } k = 0 , … , M − 1 с одинаковыми индексами k для сравниваемых процессов u и v (частоты θ u , k и θ v , k с одинаковым индексом k считаются совпадающими, если модуль их разности меньше заданной общей точности ∆ θ , т.е. | θ u , k − θ v , k | ≤ ∆ θ ); L u , k и L v , k — амплитуды k-го кубита для процессов u и v соответственно; β ≥ 0 — эмпирический коэффициент. Указанная выше экспоненциальная функция принимает наибольшее значение, если L u , k = L v , k для всех k , при этом расстояние w uv принимает наименьшее значение.

Для решения диагностической задачи для исследуемого испытуемого, представленного определенной траекторией прохождения кластеров состояний, необходимо включить соответствующую ему траекторию в выборку других допустимых траекторий. Используя вычисленную матрицу взаимных расстояний в качестве входных данных, многомерное шкалирование позволяет преобразовать представление траекторий прохождения кластеров состояний (включая траекторию, соответствующую исследуемому объекту) в диаграмму рассеяния в пространстве шкалирования заданной размерности. Основываясь на информации о принадлежности к заданным классификационным классам, дискриминантный анализ того или иного типа может выявить класс траекторий, соответствующий исследуемому объекту. Преимущества представленного подхода рассмотрены в работах [1; 8—14]. Эффективность диагностической процедуры может быть повышена путем применения методов, рассмотренных в работах [10—11].

Свертка марковского процесса в систему кубитов предполагает генерацию выборки траекторий прохождения кластеров состояний, формирующих квантовые представления, в соответствии с матрицами вероятностей переходов между состояниями марковских цепей, с использованием имитационного моделирования. Для элементов таких выборок, вычисленных для пар рассматриваемых траекторий прохождения кластеров состояний, вычисляются матрицы взаимных расстояний в спектральной метрике, после чего многомерное шкалирование позволяет представить эти траектории в виде точек в пространстве шкалирования заданной размерности.

Полученные пары множеств точек в пространстве шкалирования позволяют вычислить попарные статистики Уилкса, или Λ-статистики, которые используются для количественной оценки качества дискриминации между определенными выше парами множеств точек.

Статистики Уилкса μ для пар траекторий прохождения кластеров состояний и μ вычисляются с помощью отношения
❑ μ = det ( Υ μ ) / det ( Ω μ ) ,
где Υ μ = ‖ γ μ , ij ‖ - матрица внутригрупповых ковариаций, Ω μ = ‖ ω μ , ij ‖ — общая матрица ковариаций, γ μ , ij = ∑ α = 1 Ξ ∑ β = 1 η α , ω μ , ij = ∑ α = 1 Ξ ∑ β = 1 η α ( ζ μ , iαβ − ζ μ , i ∗ ) ( ζ μ , jαβ − ζ μ , j ∗ ) , ζ μ , lαβ — значение переменной ζ μ , l для -й сгенерированной траектории α -го варианта, l ∈ { i ; j } , ζ μ , l ∗ — среднее значение переменной ζ μ , l по всем вариантам траекторий, ζ μ , iα ∗ и ζ μ , jα ∗ — средние значения переменных ζ μ , i и ζ μ , j по всем сгенерированным траекториям α -го варианта, ζ μ , i и ζ μ , j — координаты точек, представляющих сгенерированные траектории в пространстве шкалирования, η α — число сгенерированных траекторий, относящихся к α -му варианту, Ξ — число вариантов траекторий. В данном случае Ξ = 2 .

Статистики Уилкса выступают в качестве оценок близости соответствующей исследуемому испытуемому траектории прохождения кластеров состояний и паттернам таких траекторий для распознаваемых типов испытуемых. Эти оценки «отфильтрованы» от искажений, возникающих вследствие разброса выборочных оценок элементов матриц вероятностей переходов между состояниями исходной марковской цепи.

Квантовая фильтрация

Возможность фильтрации искажений обусловлена:

  • учетом выявляемой квантовым спектральным анализом [9—10] дополнительной скрытой информации о поведении испытуемых;
  • взаимной компенсацией разнонаправленных сдвигов точек в пространстве шкалирования, что приводит к значительному снижению уровня «шума», связанного с выборочными ошибками (сдвиги вызваны искажениями элементов анализируемых матриц вероятностей переходов при вычислении статистик Уилкса для рассмотренных ранее пар выборок траекторий прохождения кластеров состояний: вычисляется «тенденция», отфильтрованная от «шума»).

Квантовая фильтрация обеспечивается выполнением вычислительной процедуры [3; 11], включающей:

  1. свертку марковских процессов, описывающих процессы обхода состояний марковской цепи, в квантовые представления (каждому рассматриваемому типу испытуемых ставится в соответствие свое квантовое представление);
  2. генерацию выборок траекторий прохождения кластеров состояний, формирующих указанные квантовые представления, в соответствии с матрицами вероятностей переходов(для каждого типа испытуемых создается свое множество траекторий прохождения кластеров состояний фиксированного объема);
  3. вычисление элементов матриц взаимных расстояний для пар множеств сгенерированных траекторий прохождения кластеров состояний в спектральной метрике с выполнением следующих условий:
    • каждой паре рассматриваемых типов испытуемых соответствует своя пара указанных сгенерированных множеств;
    • эти матрицы вычисляются для одного и того же разбиения на кластеры, полученного с использованием матрицы вероятностей переходов первого типа пары для всех траекторий, входящих в указанную пару множеств;
  4. представление указанных траекторий в виде точек в пространстве заданной размерности с помощью процедуры многомерного шкалирования;
  5. вычисление статистик Уилкса для пар сгенерированных множеств точек в пространстве шкалирования, представляющих рассматриваемые пары типов траекторий;
  6. вычисление для траекторий прохождения кластеров состояний, соответствующих исследуемым испытуемым, ближайших паттернов прохождения кластеров состояний, соответствующих их распознаваемым типам и определяющих таким образом искомый результат классификации, с использованием в качестве меры близости попарных статистик Уилкса.

Анализ деятельности пилотов на основе протоколов: пример практического применения квантовых представлений

Рассмотрим задачу оценки по данным видеоокулографии уровня сформированности навыков взаимодействия с ИУП кабины экипажа, демонстрируемой при выводе ВС из сложного пространственного положения (СПП).

Для экспериментов, которые были проведены на универсальном стенде прототипирования ГосНИИАС, привлекались пять пилотов, имеющих опыт полетов на исследуемых режимах. Информация о них в обезличенной форме представлена в табл.1.

Участник экспериментов с идентификатором EP-1, Заслуженный лётчик-испытатель РФ, рассматривался как пилот с очень высокой квалификацией, пилоты с идентификаторами EP-2 и EP-4— как квалифицированные пилоты, пилоты с идентификаторами EP-3 и EP-5— как пилоты с неизвестной квалификацией.

Таблица 1. Участники экспериментов

№

Идентификатор пилота

 

Налёт с различными видами индикации, час

 

1

EP-1

Более 12000

2

EP-2

3500

3

EP-3

1400

4

EP-4

5400

5

EP-5

1600

После консультаций с опытными пилотами, в качестве элементарных операций были использованы попадания взгляда пилота в пять зон интереса, содержащих следующие показатели: угла атаки, высоты, перегрузки, приборной скорости, угла тангажа и крена (из-за особенностей компоновки элементов индикации углы тангажа и крена были включены в одну зону интереса). Всё, что не охватывалось этими зонами, рассматривалось как условная шестая зона.

Воздействия на ручки управления при анализе не учитывались, поскольку они не регистрировались во время эксперимента. Таким образом, оценки уровня сформированности навыков взаимодействия с ИУП кабины экипажа, демонстрируемой при выводе ВС из СПП, выполнялись с использованием всего шести элементарных операций.

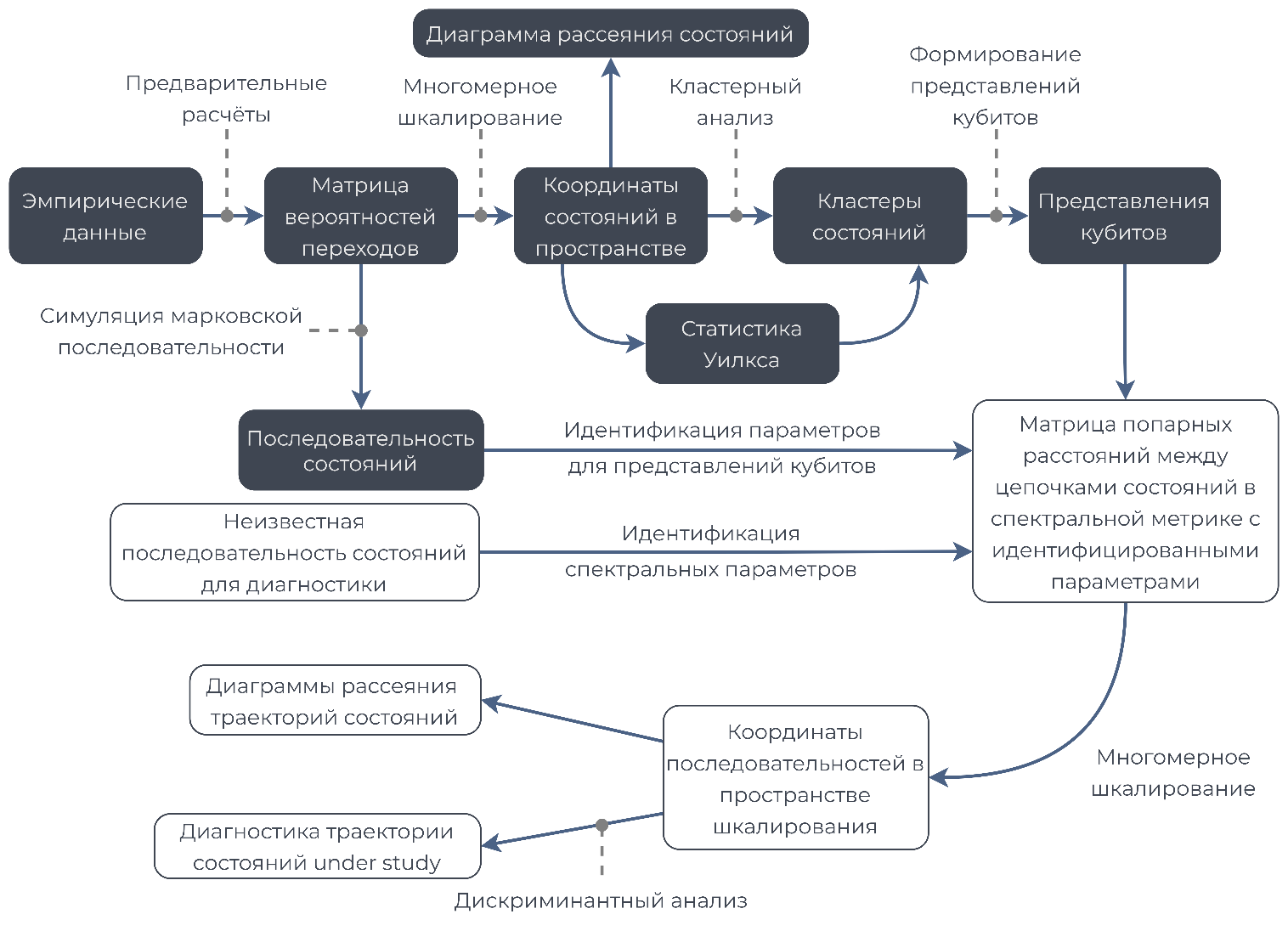
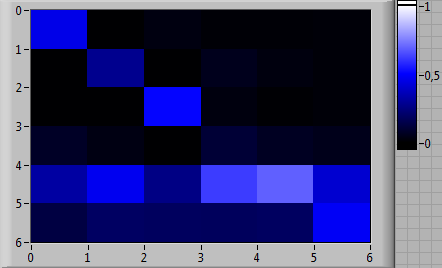
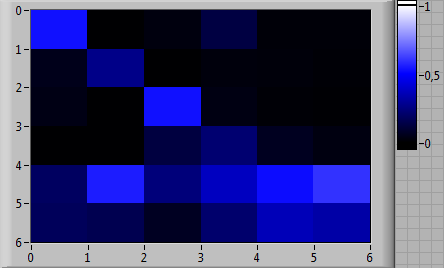
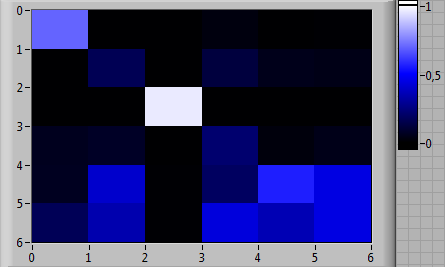
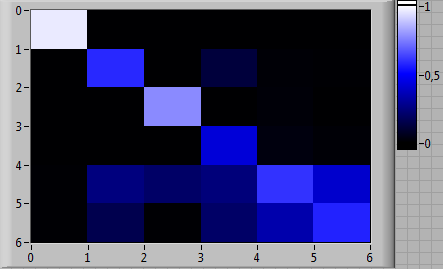
Для каждого пилота были вычислены четыре матрицы вероятностей переходов: по одной для каждого из трех вариантов выхода из СПП и одна общая для всех анализируемых вариантов выхода из СПП (таким образом, анализировалось 20 паттернов (образцов) деятельности пилотов). Общие матрицы вероятностей переходов приведены на рис. 5 (а—д) в цветовой шкале.

Применение:

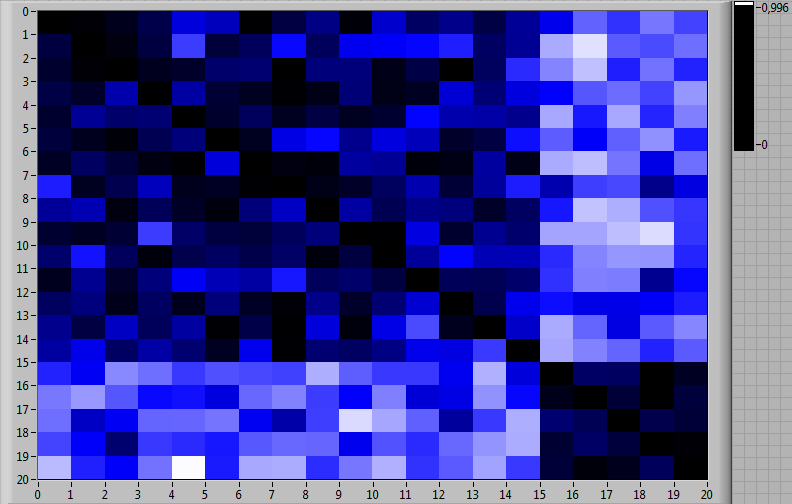
  • квантовой фильтрации с вычислением попарных статистик Уилкса ❑ μ для всех пар вариантов деятельности пилотов по выходу из СПП, обозначенных как и μ ,
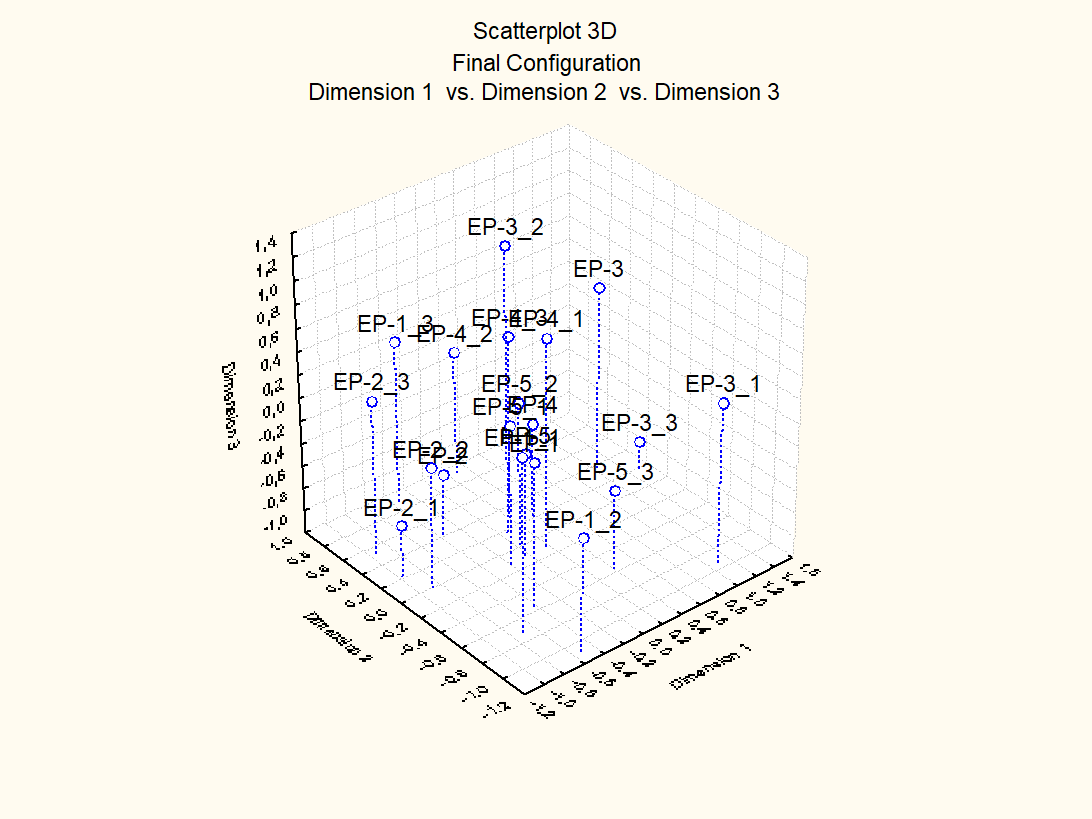
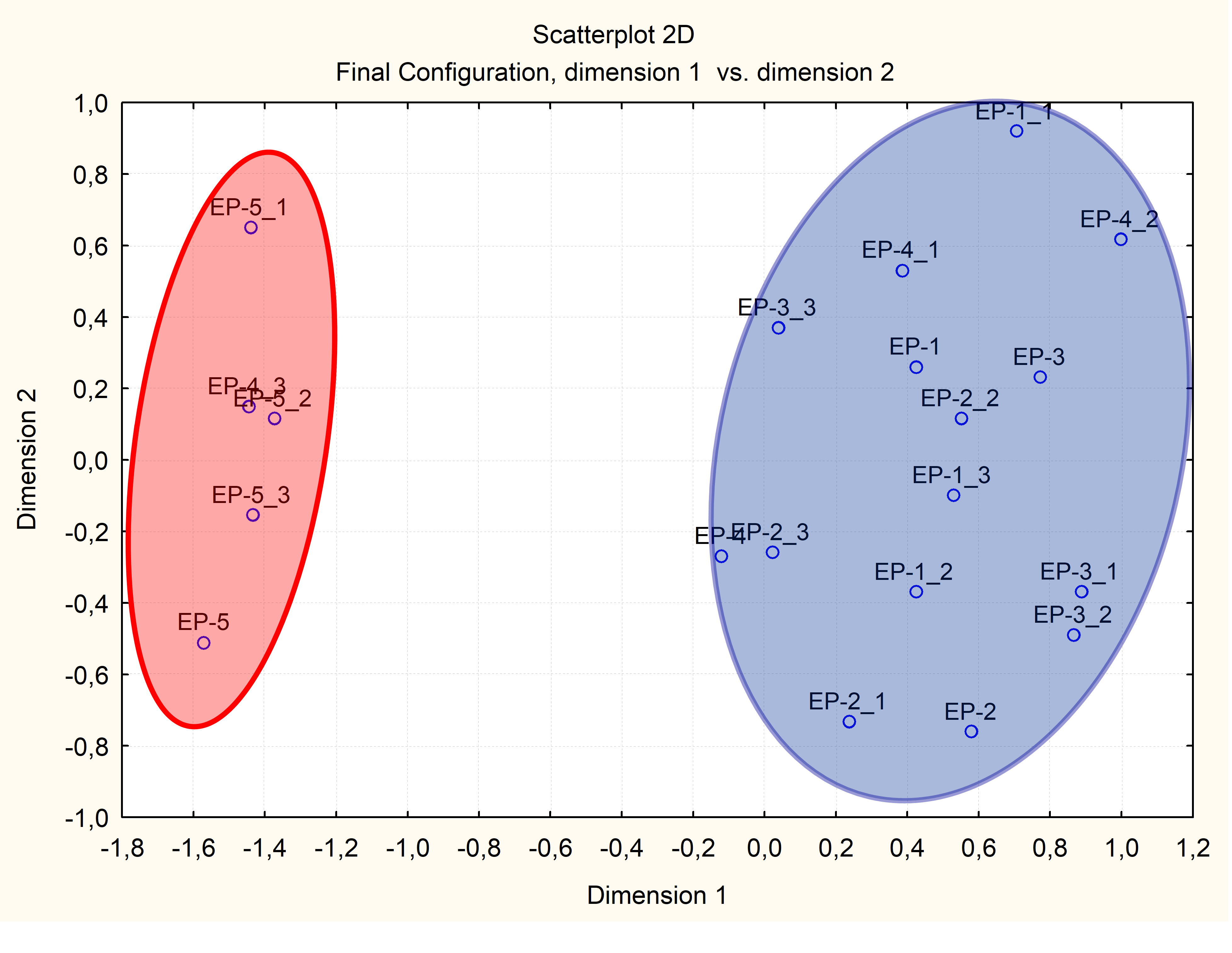
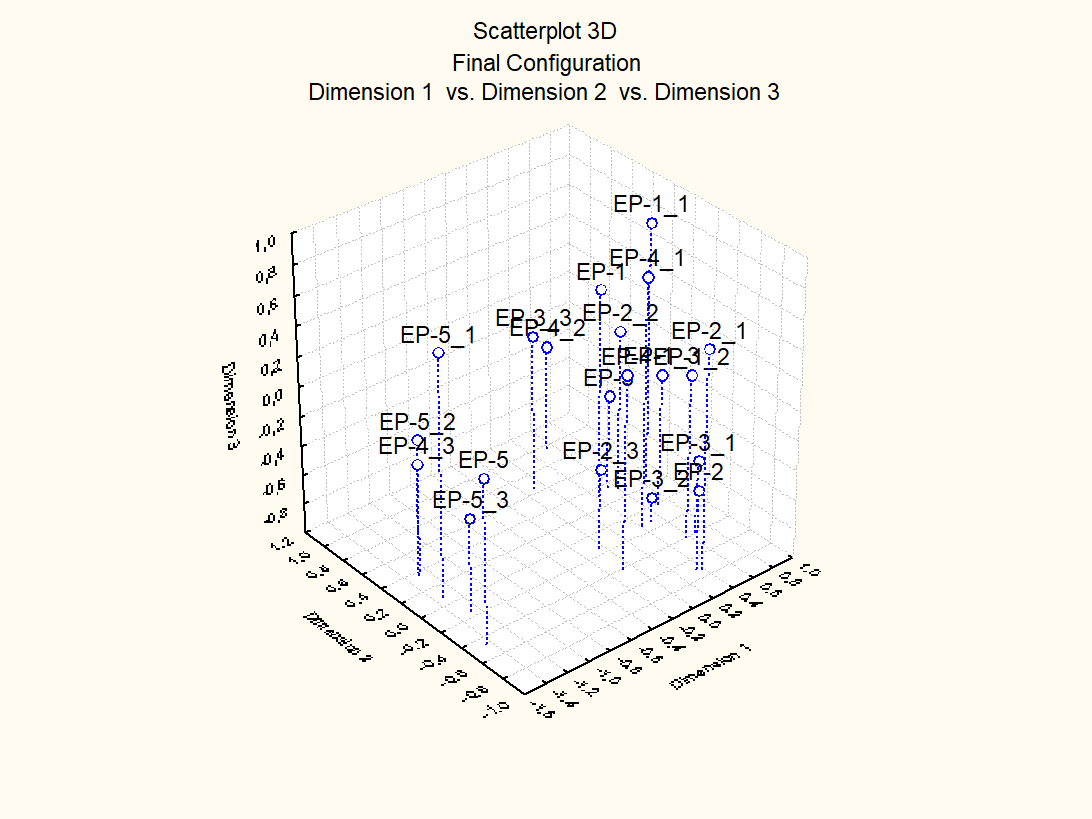
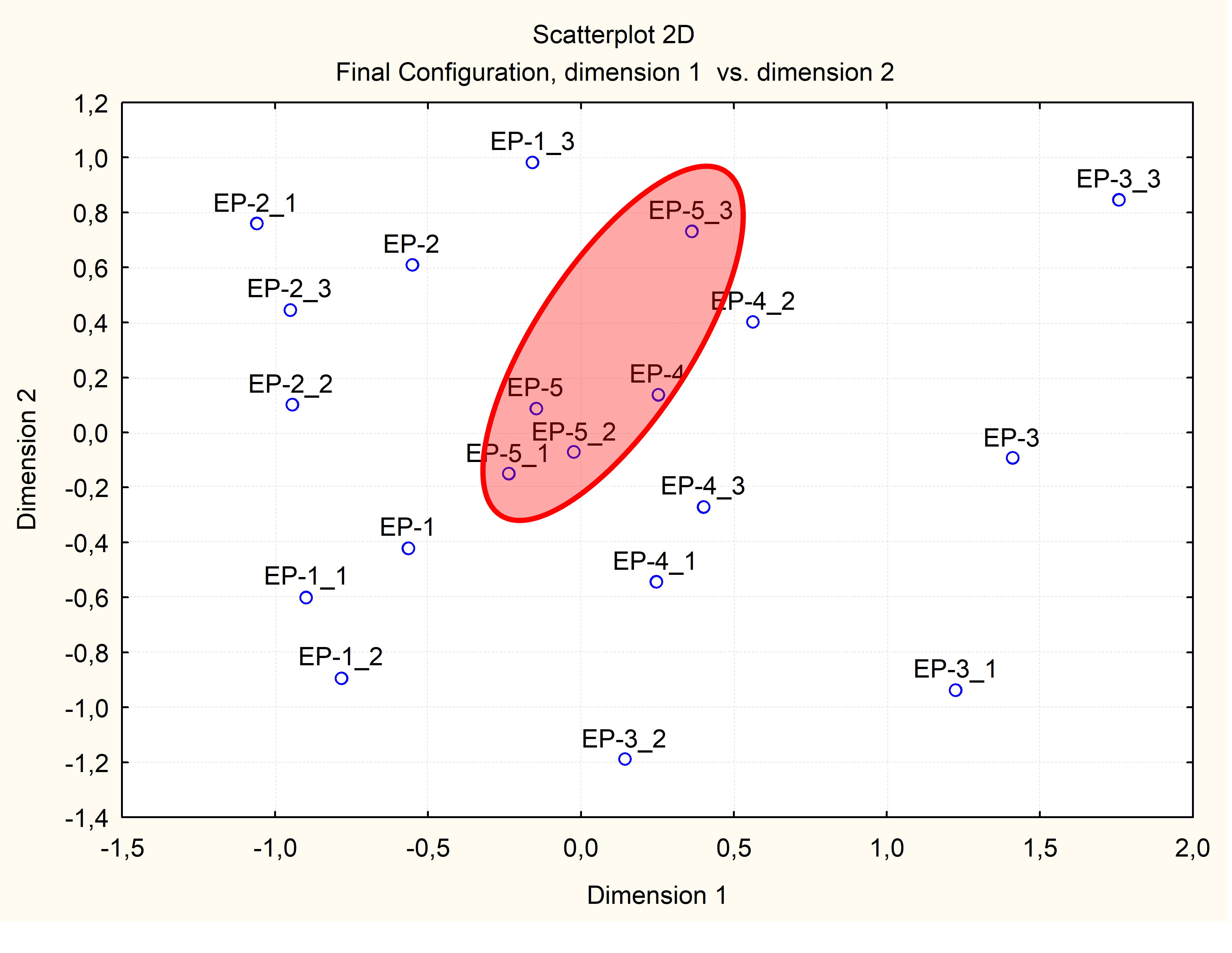
  • последующим за этим формированием матрицы взаимных расстояний Μ = ‖ m μ ‖ = (рис. 6) и заключительным шкалированием в пространствах размерности 2 и 3, - привело к распределению паттернов деятельности пилотов, показанному на рис. 7 в виде диаграмм рассеяния.

 

(а)

(б)

(в)

(г)

(д)
 

Рис. 5. Общие матрицы вероятностей переходов по трем вариантам выхода из СПП для каждого из пилотов в цветовой шкале: (а) EP-1, (б) EP-2, (в) EP-3, (г) EP-4, (д) EP-5

Рис. 6. Матрица взаимных расстояний, построенная в результате квантовой фильтрации с вычислением попарных статистик Уилкса для всех пар вариантов деятельности пилотов по выходу из СПП
 

(а)

(б)

Рис. 7. Распределение паттернов деятельности пилотов в виде диаграмм рассеяния: (а) шкалирование результатов квантовой фильтрации в пространстве размерности 2, (б) шкалирование результатов квантовой фильтрации в пространстве размерности 3

(а)

(б)

Рис. 8. Сравнение всех паттернов деятельности (а) с паттерном EP-1 и (б) с паттерном EP-5 без шкалирования, с применением только квантовой фильтрации с вычислением попарных статистик Уилкса

Результаты сравнения всех 20 паттернов деятельности с паттернами EP-1 и EP-5 без шкалирования, с применением только квантовой фильтрации с вычислением попарных статистик Уилкса { ❑ ❑ μ } μ = 1 20 и взаимных расстояний { m ❑ μ = 1 − ❑ ❑ μ } μ = 1 20 , где μ = 1 ,2 , … ,20 — индексы паттернов, а индексы ❑ соответствуют паттернам EP-1 или EP-5, представлены в виде диаграмм на рис. 8.

Диаграммы на рис. 7 и 8 показывают, что содержание деятельности пилотов EP-1, EP-2, EP-3 и EP-4 по выходу из СПП в основном группируется вокруг усредненной по попыткам квалифицированной деятельности пилота EP-1 и, в целом, не выходит за рамки разброса паттернов деятельности самого пилота EP-1. Деятельность же пилота EP-5 качественно отличается от деятельности других пилотов и, с очень высокой степенью достоверности, не укладывается в рамки такого разброса. Очевидно, что это обусловлено недостатком опыта: в отличие от других пилотов, пилотировавших различные типы ВС, этот пилот ранее летал только на одном учебно-тренировочном самолете устаревшего типа.

Учитывая очень высокую квалификацию пилота EP-1, паттерны деятельности, группирующиеся вокруг его паттернов, можно рассматривать как корректные, а паттерны, группирующиеся в области деятельности пилота EP-5, — как аномальные.

Таблица 2. Ассоциированные со статистиками Уилкса статистики F(3,13), вычисленные для пар пилотов по координатам в пространстве шкалирования

 

EP-1

EP-2

EP-3

EP-4

EP-5

EP-1

 

1,046

1,674

1,893

12,925

EP-2

1,046

 

1,018

1,600

9,971

EP-3

1,674

1,018

 

2,461

12,917

EP-4

1,893

1,600

2,461

 

5,226

EP-5

12,925

9,971

12,917

5,226

 

Таблица 3. Соответствующие статистикам F(3,13) p-значения, вычисленные для пар пилотов по координатам в пространстве шкалирования

 

EP-1

EP-2

EP-3

EP-4

EP-5

EP-1

 

0,405

0,221

0,181

0,000

EP-2

0,405

 

0,416

0,237

0,001

EP-3

0,221

0,416

 

0,109

0,000

EP-4

0,181

0,237

0,109

 

0,014

EP-5

0,000

0,001

0,000

0,014

 

Приведенные в табл. 2 и 3 F-статистики, ассоциированные со статистиками Уилкса, и соответствующие им p-значения, вычисленные для пар пилотов по координатам в пространстве шкалирования, количественно подтверждают приведенные выше качественные выводы: попарное сравнение содержания деятельности пилотов EP-1, EP-2, EP-3 и EP-4 по выходу из СПП не выявляет значимых различий ни в одной из пар (p>0,01), в то же время попарное сравнение содержания деятельности пилота EP-5 с деятельностью других пилотов (EP-1, EP-2, EP-3 и EP-4) выявляет высокозначимые (p<0,001) и значимые (p<0,015) различия в каждой паре.

Деятельность пилота EP-4 при выполнении одного из выходов из СПП является артефактом: этот опытный пилот — в отличие от других — демонстрировал во время экспериментов повышенную раздражительность и, поддавшись эмоциям, выполнил одно из лётных упражнений небрежно, не заботясь о результате.

Таким образом, количественный анализ эффективности различных вариантов взаимодействия пилотов с ИУП кабины экипажа, построенный на основе сравнений исследуемых вариантов такого взаимодействия с паттернами эмпирических данных, которые имеют известную интерпретацию, позволяет с высокой степенью достоверности отнести пилота с идентификатором EP-3 к квалифицированным пилотам, а пилота с идентификатором EP-5 — к недостаточно квалифицированным.

Полученные результаты свидетельствуют о возможности надежно отделить корректную деятельность пилотов от аномальной, используя как матрицы взаимных расстояний Μ = , где ❑ μ — попарные статистики Уилкса, так и взаимные расстояния { m ❑ μ = 1 − ❑ ❑ μ } μ = 1 N , где μ = 1 ,2 , … , N — индексы паттернов, а индексы ❑ соответствуют заданным типам деятельности.

В целом, рассмотренный подход представляет собой новый гибкий способ анализа и интерпретации сложных стохастических систем. Он может быть применен не только к деятельности пилотов, но и к анализу других человеко-машинных систем, где оказываются неэффективными традиционные методы.

Для сравнения на рис. 9 показаны результаты применения альтернативного подхода, опирающегося на оценки взаимных правдоподобий. Эти оценки вычислялись для тех же матриц вероятностей переходов, что использовались при реализации процедуры квантовой фильтрации. Попарное сравнение содержания деятельности пилота EP-5 с деятельностью других пилотов (EP-1, EP-2, EP-3 и EP-4) с использованием F-статистики свидетельствует об отсутствии значимых различий с пилотами EP-1 и EP-4 (p>0,14) и наличии значимых различий с пилотами EP-2 и EP-3 (p<0,001). Учитывая имеющиеся сведения о профессиональной квалификации пилотов, такой результат не позволяет говорить о возможности обоснованного отделения корректной деятельности пилотов от аномальной на основе анализа оценок взаимных правдоподобий. Это подтверждает вывод о том, что альтернативный подход выявляет существенно меньше значимых различий в содержании деятельности пилотов, заложенных в МВП, уступая по полноте, эффективности и качеству получаемых результатов рассмотренному выше методу, построенному на основе квантовых представлений.

(а) (б)

Рис. 9. Распределение паттернов деятельности пилотов в виде диаграмм рассеяния: (а) шкалирование оценок взаимных правдоподобий в пространстве размерности 2, (б) шкалирование оценок взаимных правдоподобий в пространстве размерности 

Основные результаты и выводы

  1. Математическая модель сопутствующей деятельности есть формальное представление деятельности пилота посредством матрицы вероятностей переходов между выполняемыми им элементарными операциями. Эта модель предназначена для использования в качестве инструмента для сравнительных оценок эффективности различных технических решений, касающихся построения ИУП кабины экипажа и управления бортовыми системами, по деятельности экипажа, включая сравнительные оценки различных способов построения мультимодального управления ВС и соответствующих им человеко-машинных интерфейсов.

  2. Зарегистрированный в результате наблюдений протокол деятельности пилота, представляющий собой последовательность дескрипторов, преобразуется в матрицу вероятностей переходов между типами элементарных операций, размер которой определяется числом учитываемых типов операций. Полученная матрица вероятностей переходов, в свою очередь, дает возможность рассматривать динамику действий пилота как марковский процесс с дискретными состояниями и дискретным временем (или марковскую цепь), состояниями которого являются учитываемые в протоколе типы элементарных операций. В общем случае, данный марковский процесс допускает полную систему связей между состояниями. Имеющая место разнотипность операций несущественна, поскольку используются только их вероятностные связи. Эффективность решения прикладной задачи регулируется степенью детализации учитываемых элементарных операций, представляющих и конкретизирующих адаптацию модели к предметной области.

  3. Выбор указанной формы математической модели обусловлен высокой эффективностью квантового спектрального анализа матриц вероятностей переходов в сочетании с квантовой фильтрацией при решении задач классификации. Альтернативный подход, который опирается на оценки взаимных правдоподобий, построенные с использованием матриц вероятностей переходов, допустим, однако этот способ выявляет существенно меньше значимых различий в содержании деятельности пилотов, уступая по полноте эффективности и качеству получаемых результатов методу, построенному на основе квантовых представлений.

  4. Анализ деятельности пилотов на основе протоколов деятельности строится на сравнениях матриц вероятностей переходов для исследуемых паттернов действий или поведения с релевантными матрицами для паттернов эмпирических данных. Эти сравнения опираются на результаты квантового спектрального анализа, обеспечивающего количественные сопоставления степени близости в спектральной метрике характеристик периодичностей выполнения типовых элементарных операций и их количеств, детально и содержательно представляя последовательности действий пилотов.

  5. Подход, опирающийся на использование квантовых представлений марковских процессов, представляет собой новый гибкий способ анализа и интерпретации сложных стохастических систем. Он может быть применен не только к деятельности пилотов, но и к анализу других человеко-машинных систем, где оказываются неэффективными традиционные методы.

Литература

  1. Грешников И.И., Куравский Л.С., Юрьев Г.А. Принципы построения программно-аппаратного комплекса для интеллектуальной поддержки экипажа и оценки уровня его подготовки // Моделирование и анализ данных. 2021. Том 11. № 2. C. 5—30. DOI:10.17759/mda.2021110201
  2. Куравский Л.С., Баранов С.Н., Юрьев Г.А. Синтез и идентификация скрытых марковских моделей для диагностики усталостного разрушения // Нейрокомпьютеры: разработка и применение. 2010. № 12. C. 20—36.
  3. Куравский Л.С., Юрьев Г.А., Юрьева Н.Е., Николаев И.А., Несимова А.О., Поляков Б.Ю., Козырев А.Д. Построение систем психологической диагностики на основе новых математических представлений // Экспериментальная психология. 2023. Том 16. № 2. C. 188—212. DOI:10.17759/exppsy.2023160212
  4. Куравский Л.С., Юрьева Н.Е., Юрьев Г.А., Порохин В.А., Грешников И.И., Златомрежев В.И. "The Intelligent System for Flight Analysis 3.3" (ISFA V. 3.3). Свидетельство о регистрации программы для ЭВМ 2021668683, 18.11.2021. Заявка № 2021668197 от 17.11.2021.
  5. Марковские модели в задачах диагностики и прогнозирования: учеб. пособие / Под ред. Л.С. Куравского. 2-е изд., доп. М.: Изд-во МГППУ, 2017. 197 с.
  6. Рубцов В.В. Социально-генетическая психология развивающего образования: деятельностный подход. М.: МГППУ, 2008. 416 с.
  7. Kuravsky L.S., Yuryev G.A. A novel approach for recognizing abnormal activities of operators of complex technical systems: three non-standard metrics for comparing performance patterns [Электронный ресурс] // International Journal of Advanced Research in Engineering and Technology (IJARET). Vol. 11(4). P. 119—136. URL: http://www.iaeme.com/IJARET/issues.asp?JType=IJARET&VType=11&IType=4 (дата обращения 21.09.2023).
  8. Kuravsky L.S. Discriminant analysis based on the approaches of quantum computing // Lobachevskii J. Math. 2020. 41(12). P. 2338—2344.
  9. Kuravsky L.S. Modeling Dynamical Behavior of Stochastic Systems: Spectral Analysis of Qubit Representations vs the Mutual Markovian Model Likelihood Estimations // Lobachevskii J. Math. 2021. 42(10). P. 2364—2376.
  10. Kuravsky L.S. Simplification of Solving Diagnostics Problems by Convolution of Applied Markovian Models into the Quantum Representations // Lobachevskii J. Math.2022. Vol. 43(7). P. 1669—1682.
  11. Kuravsky L.S., Greshnikov I.I., Yuryev G.A., and Zlatomrezhev V.I. Synthesis of Civil Aircraft Control Using Empirical Data and Quantum Filtering // Lobachevskii J. Math.2023. Vol. 44(6). P. 2079—2100.
  12. Kuravsky L.S., Yuryev G.A. Detecting Abnormal Activities of Operators of Complex Technical Systems and their Causes Basing on Wavelet Representations[Электронныйресурс] //International Journal of Civil Engineering and Technology (IJCIET). 2019. Vol. 10(2). P. 724—742. URL: http://www.iaeme.com/IJCIET/issues.asp?JType=IJCIET&VType=10&IType=2 (дата обращения 26.09.2023).
  13. Kuravsky L.S., Yuryev G.A., Zlatomrezhev V.I. New approaches for assessing the activities of operators of complex technical systems // Eksperimental’naya psikhologiya = Experimental psychology (Russia). 2019. Vol. 12. № 4. P. 27—49. DOI:10.17759/exppsy.2019120403
  14. Kuravsky L.S., Yuryev G.A., Zlatomrezhev V.I., Yuryeva N.E. Assessing the Aircraft Crew Actions with the Aid of a Human Factor Risk Model // Eksperimental’naya psikhologiya = Experimental Psychology (Russia). 2020. Vol. 13. № 2. P. 153—181. DOI:10.17759/exppsy.2020130211
  15. Lloyd E. Handbook of Applicable Mathematics. Vol. 6: Statistics / by W. Ledermann. Wiley, Hoboken, 1984.
  16. Nielsen Michael A. & Chuang Isaac L. Quantum Computation and Quantum Information. Cambridge: Cambridge University Press, 2010.
  17. von Neumann J. Mathematical Foundations of Quantum Mechanics. Princeton: Princeton Univ. Press, 1955.
  18. Wilkinson J.H. The Algebraic Eigenvalue Problem. Oxford: Clarendon Press, 1988.

Информация об авторах

Куравский Лев Семенович, доктор технических наук, профессор, декан факультета информационных технологий, Московский государственный психолого-педагогический университет (ФГБОУ ВО МГППУ), Москва, Россия, ORCID: https://orcid.org/0000-0002-3375-8446, e-mail: l.s.kuravsky@gmail.com

Козырев Алексей Денисович, аспирант, Московский государственный психолого-педагогический университет (ФГБОУ ВО МГППУ), инженер, Государственный научно-исследовательский институт авиационных систем (ФАУ «ГосНИИАС»), Москва, Россия, ORCID: https://orcid.org/0009-0008-1769-4121, e-mail: adkozyrev@2100.gosniias.ru

Грешников Иван Игоревич, кандидат технических наук, начальник сектора, Государственный научно-исследовательский институт авиационных систем (ФГУП «ГосНИИАС»), аспирант МГППУ (ФГБОУ ВО МГППУ), Москва, Россия, ORCID: https://orcid.org/0000-0001-5474-3094, e-mail: vvanes@mail.ru

Метрики

Просмотров

Всего: 16
В прошлом месяце: 11
В текущем месяце: 5

Скачиваний

Всего: 3
В прошлом месяце: 2
В текущем месяце: 1