1. ВВЕДЕНИЕ
Статья состоит из трёх частей. В первой части, принадлежащей первому автору, излагается общая агрегированная модель государства в широком смысле (близком к слову «страна»), восходящая к работам [12, 14-17, 23].
Во второй части, также принадлежащей первому автору, на основе общей модели государства, нового понятия реальной стоимости достояний, развитой в работах [2-4, 6], и новой теории денег как средства государственного управления, развитой в работах [3-11], создаётся соответствующая математическая модель в виде системы из семи дифференциальных уравнений с восемью управляющими параметрами. Эта система называется далее системой экономических уравнений государства с базисным использованием ссудного дохода. Для неё ставится оптимизационная задача нахождения оптимальных управлений при различных функционалах качества. В качестве конкретного случая рассматривается задача обеспечения максимума совокупного конечного достояния государства.
В третьей части, принадлежащей второму и третьему авторам, приводится явное аналитическое решение указанной выше оптимизационной задачи для системы экономических уравнений государства с базисным использованием ссудного дохода, которое позволяет дать эффективный численный алгоритм поиска оптимального управления. Такая авторская удача оказалась возможной на основе использования классических методов оптимального управления [1, 22] и приемов решения оптимизационных задач, разработанных в книгах [19, 21] и в статьях [18, 20]. В заключение находится численное решение задачи при одном наборе значений начальных данных, и приводятся соответствующие графики.
Статья является обобщением и развитием статьи [управление в XXI, 2006], в которой решалась оптимизационная задача для более простой базисно-надстроечной модели государства с базисным использованием ссудного дохода.
2. ОБЩАЯ АГРЕГИРОВАННАЯ МОДЕЛЬ ГОСУДАРСТВА В ШИРОКОМ СМЫСЛЕ (СТРАНЫ)
2.1. Содержательная модель государства в широком смысле (страны)
Каждое государство в широком смысле, близком к слову страна, является сложной трёхуровневой жизнедеятельной (и, в частности, организационно-производственной) подсистемой общества, устроенной в виде совокупности основных систем, связанных друг с другом в единое целое и зависящих друг от друга так, что без каждой из этих систем государство существовать не может. Основными системами государства являются: содержательная, учётная, обеспечительная, совокупная распорядительная и властная системы.
Содержательная система C осуществляет аграрный (изымающий из природной среды), индустриальный (перерабатывающий) и сервисный (обслуживающий) способы жизнедеятельности. Учётная система D осуществляет производство, сбор, хранение и раздачу денег, статистических сведений и т.п. Обеспечительная система E обеспечивает порядок, охрану, законность, нравственность и пр. Распорядительные системы F, G и H ведают деятельностью содержательной, учётной и обеспечительной систем соответственно. Властная система P осуществляет руководство совокупной распорядительной системой.
Властная система выделяет в учётной системе казначейскую систему, осуществляющую производство, сбор и хранение денег. Она называется также эмиссионным денежным центром государства. Соответственно властная система выделяет в распорядительной системе денежно-распорядительное ведомство, ведающее деятельностью казначейской системы.
Для использования денег самой содержательной системой властная система выделяет в учётной системе наряду с казначейской системой банковскую систему, осуществляющую выдачу ссудных денег и сбор долговых и временно свободных денег, и подчиняет её деятельность денежно-распорядительному ведомству.
Далее властная система разрешает банковской системе брать в долг у казначейской системы некоторое количество денег, передавать их содержательным единицам в долг с условием возврата с относительной прибавочной долей r и затем вновь возвращать в эту казначейскую систему, причём дополнительно с относительной прибавочной долей p≤r.
Содержательная, учётная и обеспечительная системы связаны с природной средой A1, внешней организованной средой A2, состоящей из зарубежных жизнедеятельных единиц и государств, и внутренней организованной средой A3, состоящей из неконтролируемых государством теневых или криминальных единиц.
Используемые государством и производимые им достояния располагаются в единицах государства и во внешних средах. Все эти достояния подразделяются на следующие виды: содержательное (код 1), распорядительное (код 2), властное (код 3), обеспечительное (код 4), учётное (код 5).
Каждая основная система производит достояние своего вида. При производстве соответствующего достояния каждая система использует некоторые из имеющихся в ней достояний. Все основные системы связаны между собой потоками производимых достояний.
Содержательная, учётная и обеспечительная системы получают из внешних сред и отдают в эти среды соответствующие достояния.
В сильно агрегированной форме устройство и функционирование государства, а также описание имеющихся в нём достояний и потоков дано на рисунке 1. На нем производимые достояния выделены квадратиком с жирным контуром. Дугами указаны преобразовательные потоки. Передаточные потоки показаны стрелками с указанием кодов на концах стрелок. Произведённые потоки обозначены прямыми входящими стрелочками, а изведённые - выходящими.
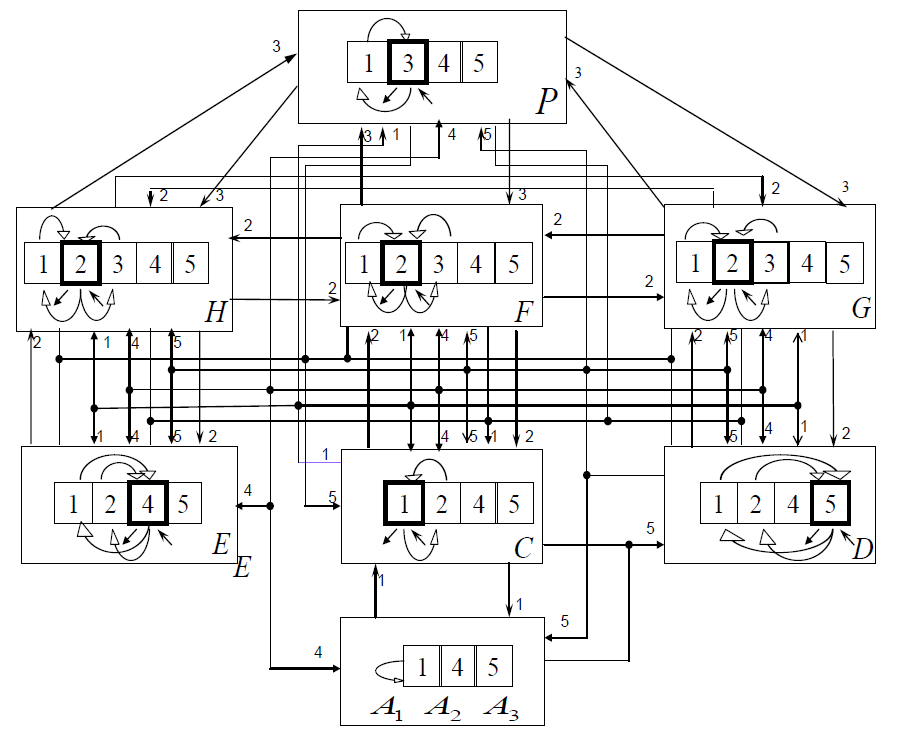
Рис. 1. Схема систем, достояний и потоков государства
2.2. Название и смысл потоков


Потоки ![]() назовем произведенными. В них включается та часть основного достояния систем C, D, E, F, G, H и P, которая «производится» именно в них, а не поступает откуда-либо извне. Здесь слово «производится» понимается в самом широком смысле. В частности, отходы деятельности считаются произведёнными в системе. Кроме того, полученный готовый товар, выставленный на продажу в каком-либо заведении и снабжённый в какой-либо форме информацией о цене, можно считать произведённым в этом заведении, поскольку над ним была произведена некоторая деятельность.
назовем произведенными. В них включается та часть основного достояния систем C, D, E, F, G, H и P, которая «производится» именно в них, а не поступает откуда-либо извне. Здесь слово «производится» понимается в самом широком смысле. В частности, отходы деятельности считаются произведёнными в системе. Кроме того, полученный готовый товар, выставленный на продажу в каком-либо заведении и снабжённый в какой-либо форме информацией о цене, можно считать произведённым в этом заведении, поскольку над ним была произведена некоторая деятельность.
3. МАТЕМАТИЧЕСКАЯ МОДЕЛЬ ГОСУДАРСТВА
Математическая модель государства создаётся на основе общей агрегированной модели государства, изложенной в первой части, посредством использования реальной денежной стоимости достояний всех видов, развитой в работах [2-4].
3.1. Система эволюционных уравнений государства в широком смысле (страны)
Система эволюционных уравнений государства составляется по следующему принципу сохранения: скорость изменения реальной стоимости достояния какого-либо вида в какой- либо основной системе равно сумме реальных стоимостей всех входящих потоков этого достояния в эту систему минус сумма реальных стоимостей всех выходящих потоков этого достояния из этой системы. В итоге получается следующая система уравнений.
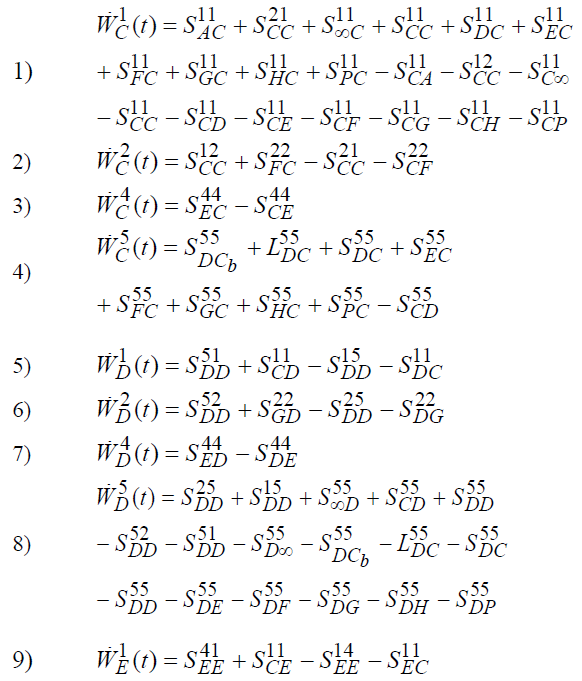
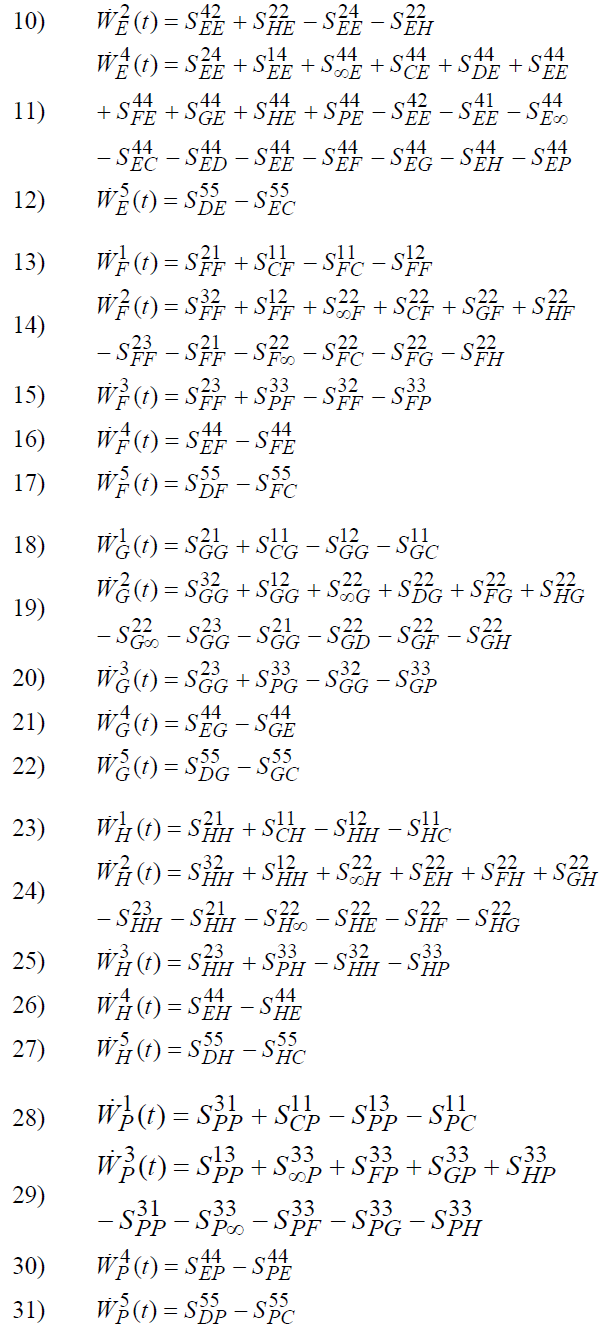
Далее составленная система эволюционных уравнений упрощается путём наложения описываемых ниже допущений для потоков достояний. Часть допущений основана на предположении о сохранении реальной стоимости достояний, другая часть допущений основана на новой теории денег как средства государственного управления, развитой в работах [3-11]. Самыми эвристическими допущениями являются допущение 14 о виде ссудного потока и допущение 15 о виде изводных потоков.
3.2. Допущения для потоков
1. Считаем, что послесодержательные потоки и содержательные потоки имеют одинаковую реальную стоимость, т.е.
![]()
2. Считаем, что предотходные потоки и отходные потоки имеют одинаковую отрицательную реальную стоимость, т.е.
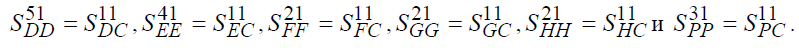
3. Считаем, что обменные потоки между распорядительными системами равны, т.е.
![]()
4. Считаем, что преддокладные и докладные потоки имеют одинаковую реальную стоимость, т.е.
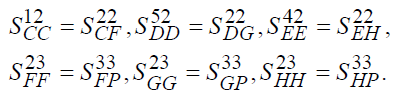
5. Считаем, что послеприказные и приказные потоки имеют одинаковую реальную стоимость, т.е.
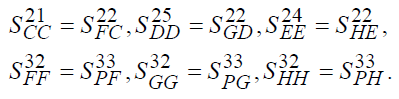
6. Считаем, что из каждой не содержательной системы в «обмен» на предметно-трудовую компоненту (см. далее) уходит в содержательную систему учётного достояния столько, сколько его приходит в систему из учётной системы, т.е.
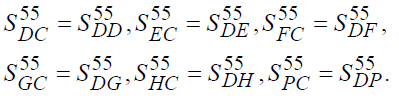
Эти равенства означают равенство денежных предметно-трудовых и казённораздаточных потоков.
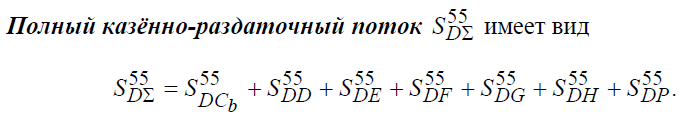
Следовательно, из учётной системы в содержательную систему уходит полный поток ![]() , в котором третье слагаемое учётная система передаёт не казённой части содержательной системы в «обмен» на свою собственную предметно-трудовую компоненту
, в котором третье слагаемое учётная система передаёт не казённой части содержательной системы в «обмен» на свою собственную предметно-трудовую компоненту
![]()
Предметно-трудовые потоки в конечном итоге переходят к содержательной системе и возвращаются из неё в учётную систему в виде возвратно-налоговых сборов.
При этом полный налоговый сбор ![]() равен полному казённо-раздаточному потоку минус процентная часть от ссуды, полученной содержательной системой, т.е.
равен полному казённо-раздаточному потоку минус процентная часть от ссуды, полученной содержательной системой, т.е.
![]()
Поэтому полный возвратно-налоговый сбор ![]() имеет вид
имеет вид ![]()
8. Считаем, что силовые и силовые возвратные потоки имеют одинаковую реальную стоимость, т.е.
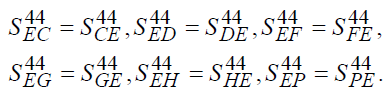
9. Напомним, что изведённые потоки ![]() представляются в виде суммы
представляются в виде суммы ![]()
переработанного потока ![]() и износного потока
и износного потока ![]() .
.
Считаем, что соответствующая предметно-трудовая компонента не содержательной системы (т.е. стоящая в левой части приводимого ниже соответствующего равенства) оплачивается этой системой передаваемым ею содержательной системе предметнотрудовым денежным потоком, а значит, согласно равенствам их пункта 6 и получаемым этой системой казённо-раздаточным денежным потоком, т.е.
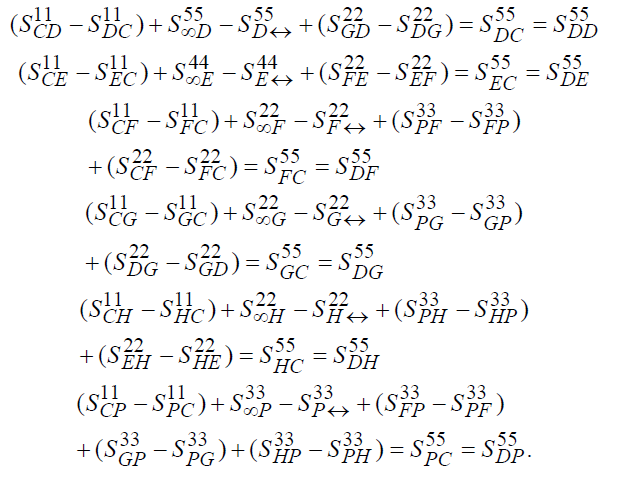
Здесь первые слагаемые ![]() , стоящие в скобках, называются предметными компонентами не содержательных систем M, а суммы остальных слагаемых называются трудовыми компонентами не содержательных систем M.
, стоящие в скобках, называются предметными компонентами не содержательных систем M, а суммы остальных слагаемых называются трудовыми компонентами не содержательных систем M.
Эти равенства означают, что казённо-раздаточные потоки ![]() состоят из предметной части, предназначенной для оплаты соответствующей системой приходного и отходного содержательных достояний, и трудовой части, предназначенной для оплаты трудовой деятельности в системе.
состоят из предметной части, предназначенной для оплаты соответствующей системой приходного и отходного содержательных достояний, и трудовой части, предназначенной для оплаты трудовой деятельности в системе.
10. Считаем, что предметно-трудовая компонента содержательной системы (т.е. стоящая в левой части приводимого ниже равенства) финансируется учётной системой передаваемым ею содержательной системе ссудным денежным потоком, т.е.
![]()
11. Полный приходно-отходный поток ![]() имеет вид
имеет вид
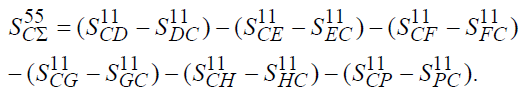
Используя равенства из пункта 9, получаем
![]()
где 0<pi<1 для всех i. Числа pi показывают части казённо-раздаточных потоков ![]() , идущие на оплату не содержательными системами M своих предметных (приходно-отходных) компонент
, идущие на оплату не содержательными системами M своих предметных (приходно-отходных) компонент ![]() . Соответственно, числа 1 — pi показывают части казённо-раздаточных потоков, идущие на оплату не содержательными системами M=D,E,F,G,H,P своих трудовых компонент.
. Соответственно, числа 1 — pi показывают части казённо-раздаточных потоков, идущие на оплату не содержательными системами M=D,E,F,G,H,P своих трудовых компонент.
Показатели pi предметно-трудового распределения казённо-раздаточных потоков ![]() устанавливают сами не содержательные системы M, исходя из общих установок властной системы на данном временном промежутке.
устанавливают сами не содержательные системы M, исходя из общих установок властной системы на данном временном промежутке.
12. Считаем, что денежные казённо-раздаточные потоки ![]() состоят из двух частей: из бюджетной части
состоят из двух частей: из бюджетной части ![]() (здесь буква В от слова «budget») и процентно-ссудной части
(здесь буква В от слова «budget») и процентно-ссудной части ![]() , т.е.
, т.е.
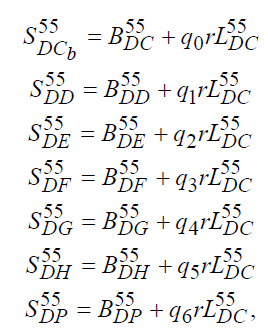
где ![]()
Полный бюджетно-раздаточный поток ![]() имеет вид
имеет вид
![]()
Тогда полный казённо-раздаточный поток ![]() принимает вид
принимает вид ![]() . Следовательно, полный налоговый сбор равняется полному бюджетному потоку, т.е.
. Следовательно, полный налоговый сбор равняется полному бюджетному потоку, т.е. ![]() .
.
Денежные казённо-раздаточные потоки ![]() предназначены для осуществления добровольно-принудительного изъятия части производимого содержательного достояния из содержательной системы C и передачи его в казённые системы M=Cb,D,E,F,G,H,P. Основными способами такого изъятия являются изъятие посредством налогов и изъятие посредством ссуд.
предназначены для осуществления добровольно-принудительного изъятия части производимого содержательного достояния из содержательной системы C и передачи его в казённые системы M=Cb,D,E,F,G,H,P. Основными способами такого изъятия являются изъятие посредством налогов и изъятие посредством ссуд.
Изъятие посредством налогов предназначено изымать содержательное достояние в размере, равном полному бюджетно-раздаточному потоку ![]() . Изъятие посредством ссуд предназначено изымать содержательное достояние в размере, равном процентной части
. Изъятие посредством ссуд предназначено изымать содержательное достояние в размере, равном процентной части ![]() , полученной избранным вводчиком от выданной содержательной системе ссуды
, полученной избранным вводчиком от выданной содержательной системе ссуды ![]() . Именно ссудную часть
. Именно ссудную часть ![]() властная система раздаёт указанным казённым системам M в соответствии с показателями qi распределения процентно-ссудного потока
властная система раздаёт указанным казённым системам M в соответствии с показателями qi распределения процентно-ссудного потока![]() . Показатели qi устанавливает властная система, исходя из собственных целей, задач и предпочтений на данном временном промежутке.
. Показатели qi устанавливает властная система, исходя из собственных целей, задач и предпочтений на данном временном промежутке.
13. Будем считать, что ссудный поток ![]() прямо пропорционален произведению
прямо пропорционален произведению ![]() и обратно пропорционален учётной ставке r и полному бюджетному потоку
и обратно пропорционален учётной ставке r и полному бюджетному потоку![]() , т.е. он имеет вид
, т.е. он имеет вид
![]()
где число K>0 обозначает наибольшую предельно возможную величину содержательного достояния содержательной системы, числа ![]() показывают степень влияния соответствующих факторов на ссудную востребованность, а числа a, c, d>0 представляют собой размерностные коэффициенты.
показывают степень влияния соответствующих факторов на ссудную востребованность, а числа a, c, d>0 представляют собой размерностные коэффициенты.
В развёрнутом виде получаем
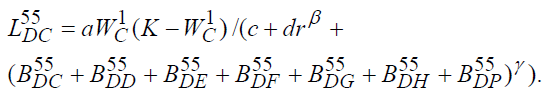


3.3. Система экономических уравнений государства в широком смысле (страны)
Применяя все указанные связи между потоками к системе эволюционных уравнений, получаем следующую систему дифференциальных уравнений:
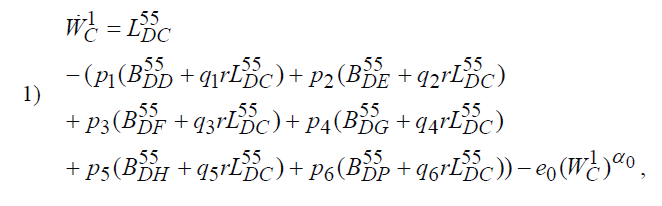
где
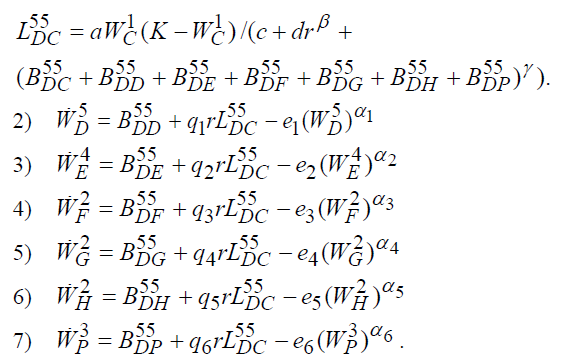
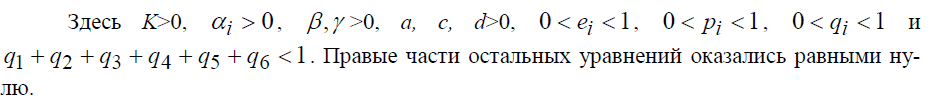
Эту систему можно назвать системой экономических уравнений государства (в широком смысле). Первое уравнение этой системы естественно назвать основным экономическим уравнением государства.
3.4. Оптимизационная задача для системы экономических уравнений государства
В полученной выше системе экономических уравнений параметры ![]() являются управлениями.
являются управлениями.
Из самого вида экономических уравнений вытекают следующие непосредственные выводы.
1. Увеличение бюджетных раздач ![]() казённым системам M=Cb,D,E,F,G,H,P приводит к приращению их основных достояний. Однако это приводит и к одновременному убыванию содержательного достояния содержательной системы C как за счёт уменьшения ссудного заимствования, так и за счёт увеличения предметных отдач
казённым системам M=Cb,D,E,F,G,H,P приводит к приращению их основных достояний. Однако это приводит и к одновременному убыванию содержательного достояния содержательной системы C как за счёт уменьшения ссудного заимствования, так и за счёт увеличения предметных отдач ![]() казённым системам M.
казённым системам M.
2. Увеличение учётной ставки r также приводит к приращению основных достояний указанных казённых систем. Однако, как и ранее, это приводит и к одновременному убыванию содержательного достояния содержательной системы C как за счёт уменьшения ссудного заимствования, так и за счёт увеличения предметных отдач ![]() казённым системам M.
казённым системам M.
Из сказанного следует, что властная система государства должна решать оптимизационную задачу на выбор оптимизирующих управлений ![]() в системе экономических уравнений в соответствии с поставленными целями на временном промежутке [to,T]. При этом оптимизирующие управления должны быть ограничены как снизу, так и сверху следующими числовыми неравенствами:
в системе экономических уравнений в соответствии с поставленными целями на временном промежутке [to,T]. При этом оптимизирующие управления должны быть ограничены как снизу, так и сверху следующими числовыми неравенствами:
![]()
Например, возможной целью может быть достижение к моменту времени T относительно начального момента времени to наибольшего значения целевой функции прироста совокупного достояния
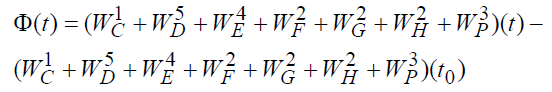
Формально это можно записать в виде ![]() .
.
Ясно, что это равносильно обеспечению максимума совокупного конечного достояния государства, т.е.
![]()
Поскольку система экономических уравнений государства является сложной, естественно пытаться решать поставленную оптимизационную задачу в нескольких более простых случаях.
3.5. Основная упрощенная система экономических уравнений государства
Рассмотрим упрощённый вариант этой системы.
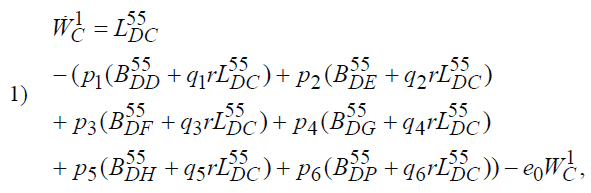
где
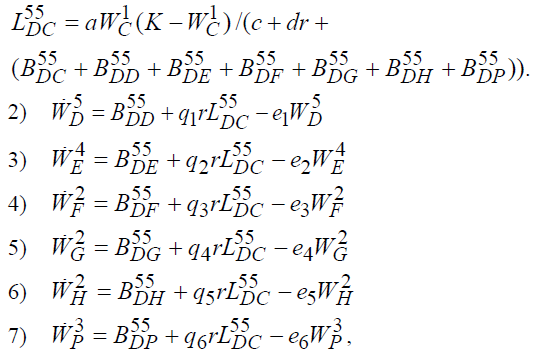
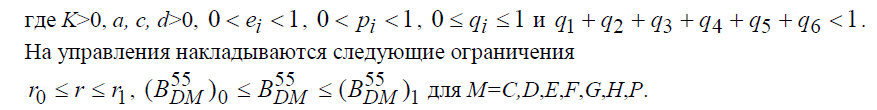
Эту систему можно назвать основной упрощённой системой экономических уравнений государства.
3.6. Упрощенная система экономических уравнений государства при базисном использовании ссудного дохода

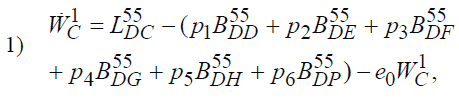
где
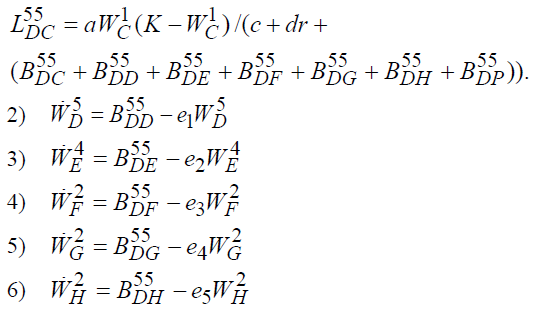
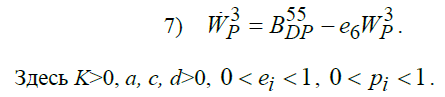
На управления накладываются следующие ограничения
![]()
Эту систему можно назвать упрощённой системой экономических уравнений государства при базисном использовании ссудного дохода.
Интерес представляет нахождение оптимального решения последней системы при следующих числовых данных:
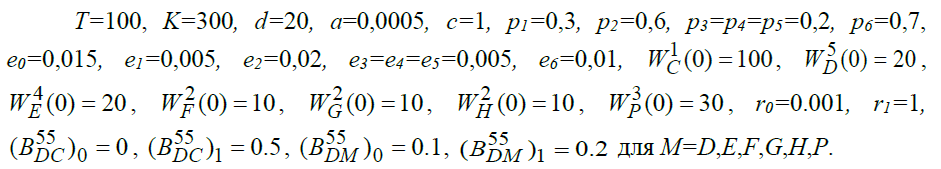
4. РЕШЕНИЕ ОПТИМИЗАЦИОННОЙ ЗАДАЧИ ДЛЯ МОДЕЛИ ГОСУДАРСТВА ПРИ БАЗИСНОМ ИСПОЛЬЗОВАНИИ ССУДНОГО ДОХОДА
4.1. Постановка задачи оптимального управления


Особенность этой задачи заключается в том, что управляющая система является нелинейной, поскольку управления входят в уравнения нелинейным образом. Тем не менее, удаётся найти явное аналитическое решение.
4.2. Решение задачи на основе принципа максимума
Для решения поставленной оптимизационной задачи будем использовать принцип максимума Понтрягина. В этом случае сопряженная система имеет вид



Логарифм, в последнем выражении, есть либо ареатангенс, либо ареакотангенс (в зависимости от знака, с которым будет раскрыт модуль). При данном сочетании параметров, этот модуль следует раскрывать со знаком «-», что соответствует ареакотангенсу. Тогда,
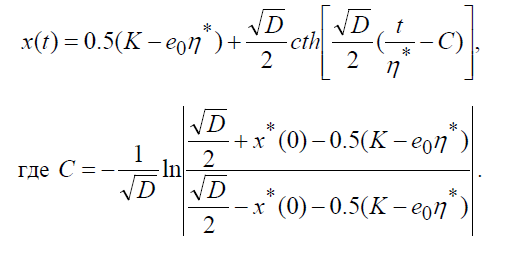

4.3. Численное решение оптимизационной задачи

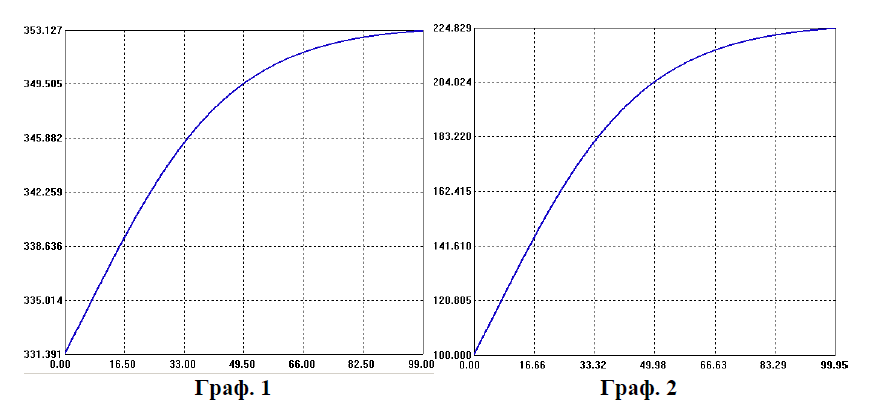
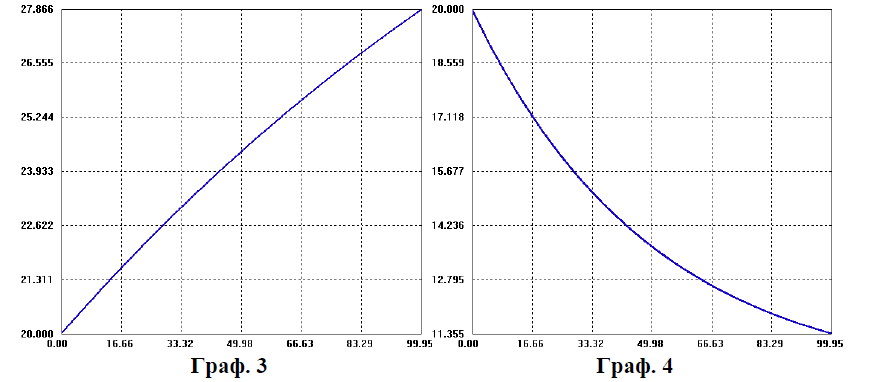
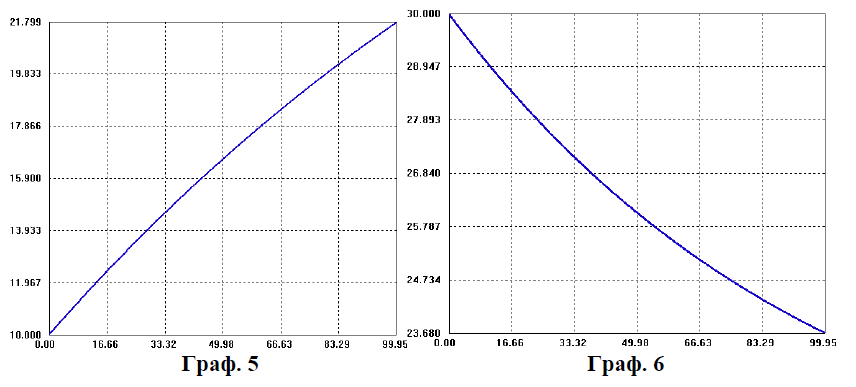
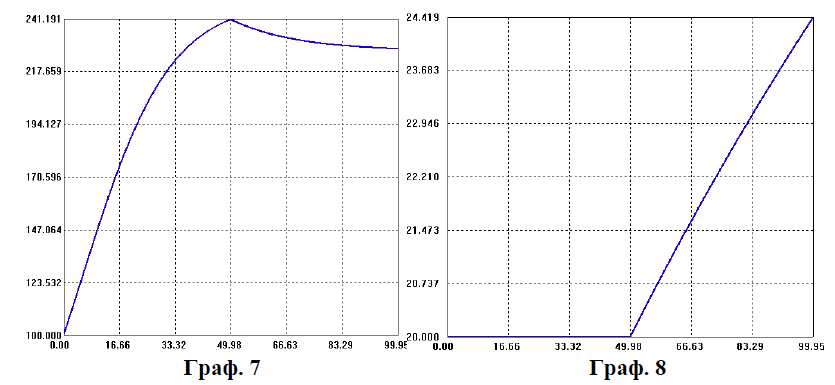
Рис. 2.
Из структуры оптимального управления видно, что оно кусочно-постоянное. Следовательно, фазовые траектории, соответствующие оптимальному решению будут состоять из кусков фазовых траекторий, соответствующих постоянным значениям управляющих параметров. Проведем качественный анализ системы (1),(2) при постоянных значениях управляющих параметров. Сначала найдем стационарные значения переменной х. Для этого приведем к общему знаменателю правую часть уравнения (1) и найдем корни квадратного трехчлена, образовавшегося в числителе полученного дробного выражения. Дискриминант этого трехчлена имеет вид
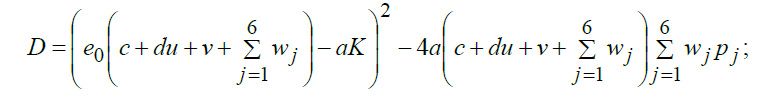
корни записываются следующим образом
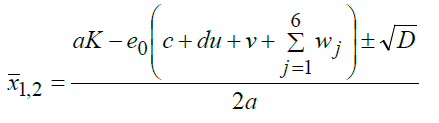

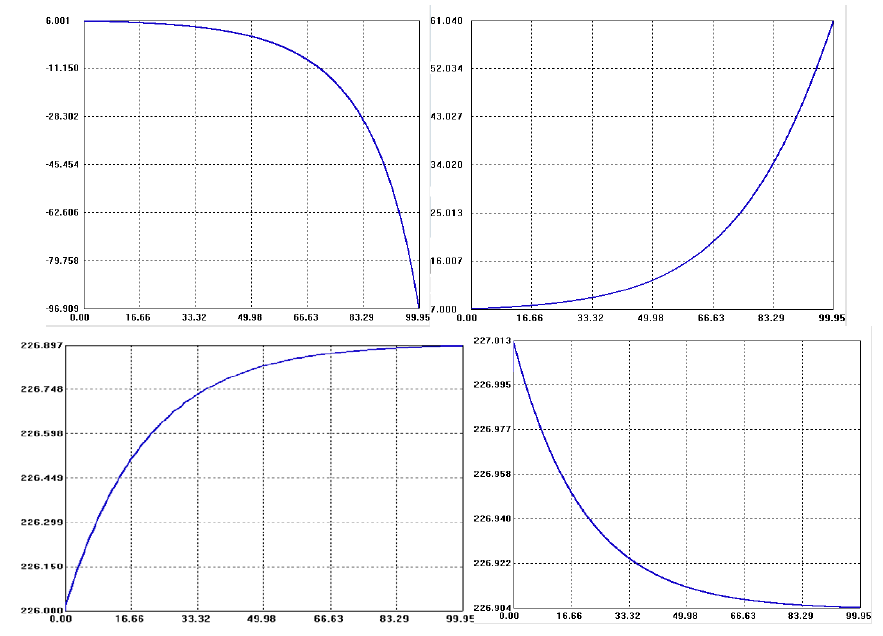
Рис. 3.

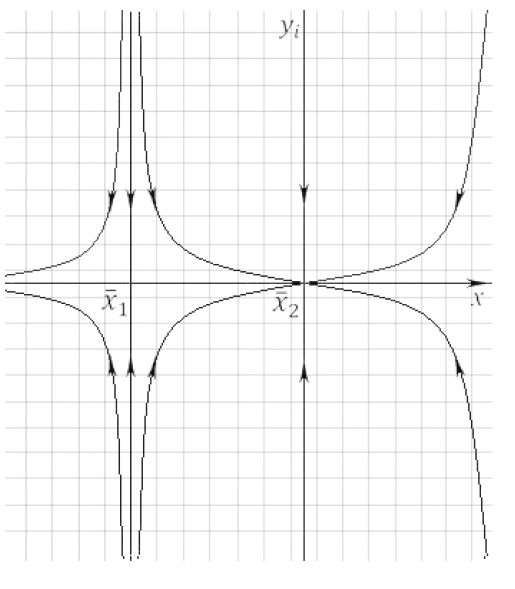
Рис. 4
На рисунке 5 приведены результаты исследования значения целевого функционала от ресурса управления. В ходе исследования изменялась величина верхней границы w1 ограничений на значение управляющего параметра w1 и определялась величина критерия качества. Результаты исследования показывают, что при увеличении ресурса управления значение критерия качества монотонно возрастают, причем рост близок к линейному.
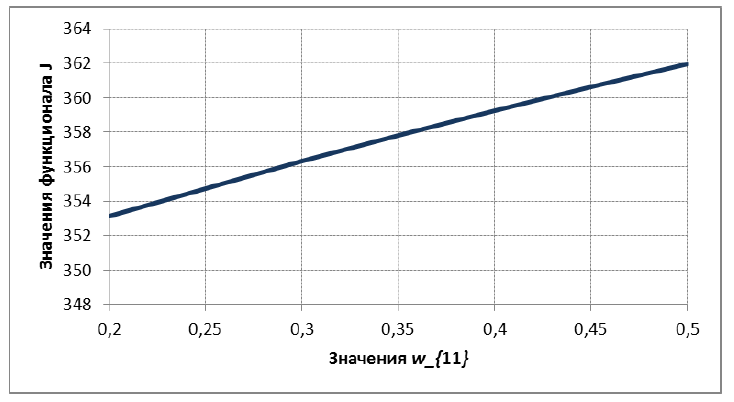
Рис. 5
На рисунке 6 приведены результаты исследования зависимости значения целевого функционала от параметра e0. В ходе исследования изменялось значение параметра e0 и
определялась величина критерия качества. Результаты исследования показывают, что при увеличении параметра е0 значение критерия качества монотонно убывает, причем убывание близко к линейному.
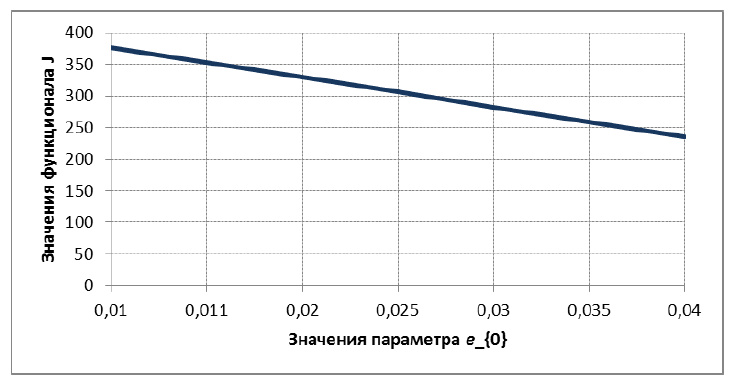
Рис. 6

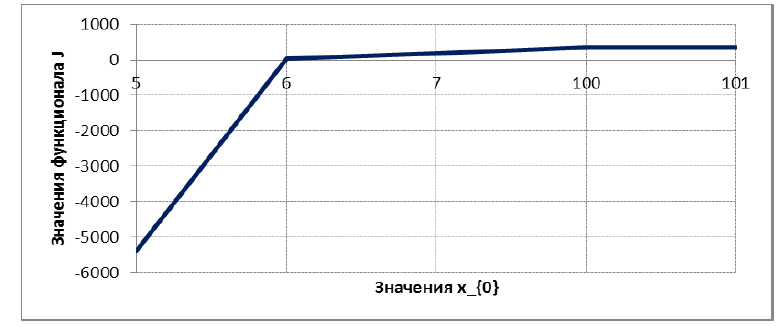
Рис. 7
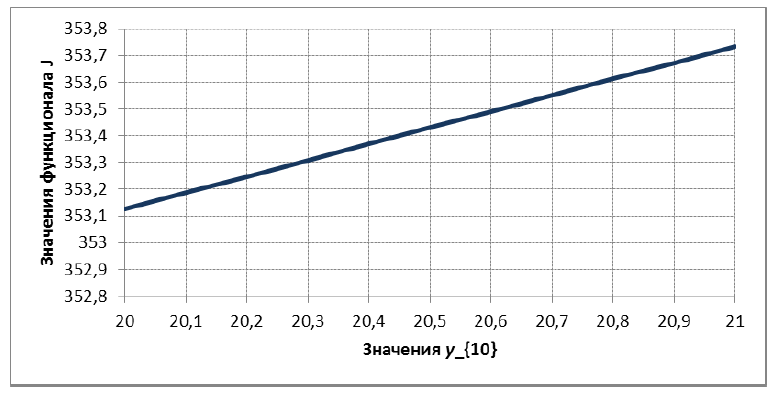
Рис. 8